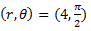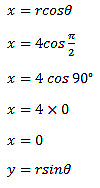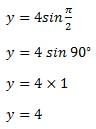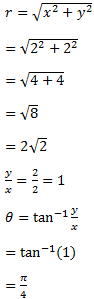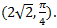Cartesian and polar coordinates in three dimensions | Mathematics for Grade 12 PDF Download
| Table of contents |

|
| Introduction |

|
| Polar Coordinates Formula |

|
| Cartesian to Polar Coordinates |

|
| 3D Polar Coordinates |

|
| Polar Coordinates Examples |

|
Introduction
- When each point on a plane of a two-dimensional coordinate system is decided by a distance from a reference point and an angle is taken from a reference direction, it is known as the polar coordinate system.
- Pole = The reference point
Polar axis = the line segment ray from the pole in the reference direction - In the polar coordinate system, the origin is called a pole.
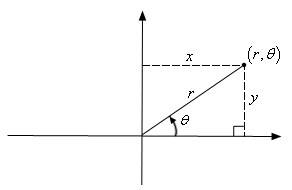
- Here, instead of representing the point as (x, y), we can express it as a polar coordinate (r, θ).
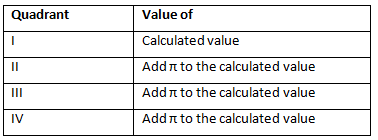
Where the value of r can be negative. The value of angle changes based on the quadrant in which the r lies.

Note:
In the Cartesian coordinate system, the distance of a point from the y-axis is called its x-coordinate and the distance of a point from the x-axis is called its y-coordinate.
Polar grid
Polar grid with different angles as shown below: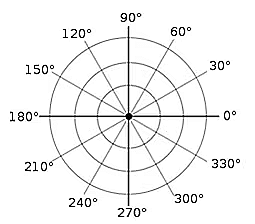
Also, π radians are equal to 360°.
Polar Coordinates Formula
We can write an infinite number of polar coordinates for one coordinate point, using the formula
- (r, θ+2πn) or (-r, θ+(2n+1)π), where n is an integer.
- The value of θ is positive if measured counterclockwise.
- The value of θ is negative if measured clockwise.
- The value of r is positive if laid off at the terminal side of θ.
- The value of r is negative if laid off at the prolongation through the origin from the terminal side of θ.
Note:
The side where the angle starts is called the initial side and the ray where the measurement of the angle stops is called the terminal side.
Cartesian to Polar Coordinates
x = r cos θ
y = r sin θ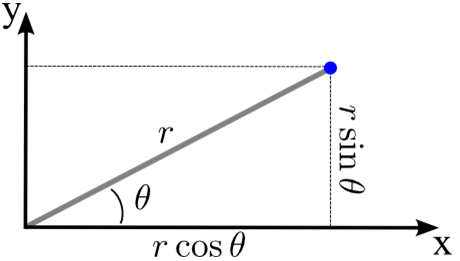
Finding r and θ using x and y: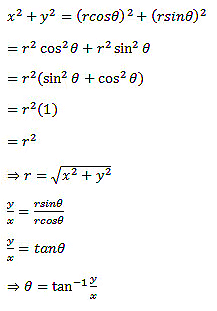
3D Polar Coordinates
- 3d polar coordinates or spherical coordinates will have three parameters: distance from the origin and two angles.
- The 3d-polar coordinate can be written as (r, Φ, θ).
- Here,
R = distance of from the origin
Φ = the reference angle from XY-plane (in a counter-clockwise direction from the x-axis)
θ = the reference angle from z-axis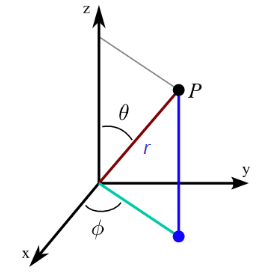
Polar Coordinates Examples
Example 1: Convert the polar coordinate (4, π/2) to a rectangular point.
Sol:
Given,
We know that,Hence, the rectangular coordinate of the point is (0, 4).
Example 2: Convert the rectangular or cartesian coordinates (2, 2) to polar coordinates.
Sol:
Given, (x, y)=(2, 2)
Hence, the polar coordinates are
Note:
We know that, the value of r can be negative too.
That means r = ±2√2
Also, tan⁻¹(1) will also take many values, such as 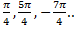
Hence, the possible polar coordinates of a point (2, 2) are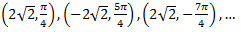
|
270 videos|267 docs|155 tests
|
FAQs on Cartesian and polar coordinates in three dimensions - Mathematics for Grade 12
| 1. What are polar coordinates and how do they differ from Cartesian coordinates? |  |
| 2. How can you convert Cartesian coordinates to polar coordinates? |  |
| 3. What are the formulas for 3D polar coordinates? |  |
| 4. What are some common applications of polar coordinates? |  |
| 5. How do polar and Cartesian coordinates relate in three dimensions? |  |