हल किए गए उदाहरण: अनुपात और समानुपात | गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 2 - CTET & State TET PDF Download

अनुपात और अनुपात

दो मात्राओं की तुलना को विभाजन द्वारा अनुपात कहा जाता है और दो अनुपातों की समानता को अनुपात कहा जाता है। अनुपात को विभिन्न रूपों में लिखा जा सकता है जैसे x : y या x/y और इसे सामान्यतः पढ़ा जाता है, x is to y।

दूसरी ओर, अनुपात एक समीकरण है जो कहता है कि दो अनुपात समान हैं। अनुपात को x : y : : z : w के रूप में लिखा जाता है, और इसे पढ़ा जाता है x is to y as z is to w। यहाँ, x/y = z/w जहाँ w और y शून्य के समान नहीं हैं।

हल किए गए उदाहरण

उदाहरण 1: एक सड़क निर्माण परियोजना का वार्षिक बजट $25,200 है जिसे 12 महीनों में समान रूप से वितरित किया गया है। यदि तीसरे महीने के अंत तक वास्तविक खर्च $7,420 हो गया है, तो निर्माण परियोजना बजट से कितना अधिक हो गया है? (a) $2150 (b) $3340 (c) $1120 (d) $980 (e) $1640 उत्तर: (c) मासिक बजट ज्ञात करने के लिए:

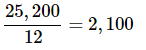
जो 3 महीनों के लिए बजट है: 2,100 x 3 = 6,300। यह जानने के लिए कि वे बजट से कितना अधिक हैं, बजट की गई राशि को वास्तविक खर्चों में से घटाया जाता है। 7,420 − 6,300 = 1,120

उदाहरण 2: दुक्लि ऑफ ग्रैंड फेनविक एक असामान्य मुद्रा प्रणाली का उपयोग करता है। 1 बड़े फेनविक को बनाने के लिए 24 छोटे फेनविक की आवश्यकता होती है। वर्तमान विनिमय दरों पर, 1 बड़ा फेनविक $3.26 अमेरिकी मुद्रा के लिए विनिमय किया जा सकता है। एक अमेरिकी पर्यटक $300 के लिए ग्रैंड फेनविक मुद्रा में कितने फेनविक का विनिमय कर सकता है (नजदीकी छोटे फेनविक में गोल किया गया)? (a) 92 बड़े फेनविक और 1 छोटा फेनविक (b) 40 बड़े फेनविक और 18 छोटे फेनविक (c) 108 बड़े फेनविक और 16 छोटे फेनविक (d) 296 बड़े फेनविक और 16 छोटे फेनविक (e) उपरोक्त में से कोई नहीं उत्तर: (a) $3.26 को 1 बड़े फेनविक के लिए विनिमय किया जा सकता है, या, समान रूप से, 24 छोटे फेनविक के लिए। हम एक अनुपात कथन स्थापित कर सकते हैं, जहाँ F उन छोटे फेनविक की संख्या है जिनके लिए $300 का विनिमय किया जा सकता है:

उत्तर है 2,209 छोटे फेनविक्स, जिन्हें भाग देकर गिना जा सकता है: 2,209 ÷ 24 = 92 शेष 1 या 92 बड़े फेनविक्स और 1 छोटा फेनविक।

उदाहरण 3: अनुपात 3 से 1/2 समान है अनुपात: (क) 1 से 6 (ख) 3 से 2 (ग) 2 से 3 (घ) 6 से 1 (ङ) 5 से 1 उत्तर: (घ) अनुपात 3 से 1/2 वही है जो 6 से 1 के अनुपात के बराबर है।

इसके अलावा, यदि आप अनुपात के दोनों पक्षों को दोगुना करते हैं, तो आपको 6 से 1 मिलता है।

उदाहरण 4: अनुपात 4 से 1/4 समान है निम्नलिखित में से किस अनुपात के? (क) 8 से 1 (ख) 12 से 1 (ग) 16 से 1 (घ) 16 से 3 (ङ) 6 से 1 उत्तर: (ग) अनुपात 4 से 1/4 समान है जो 16 से 1 है।

16 को अनुपात 16 से 1 के रूप में लिखा जा सकता है।

उदाहरण 5: एक मानचित्र पर, एक और आधा इंच साठ वास्तविक मील को दर्शाता है। N के संदर्भ में, मानचित्र पर N इंच द्वारा दर्शाए गए वास्तविक मील की दूरी क्या है? (क) 45N मील (ख) 40/N मील (ग) 40N मील (घ) 90/N मील (ङ) 90 N मील उत्तर: (ख) मान लें कि x वास्तविक मील की संख्या है। फिर अनुपात का कथन स्थापित किया जाएगा, जिसमें प्रत्येक अनुपात वास्तविक मील की संख्या है मानचित्र के इंच के लिए: बाएं अभिव्यक्ति को सरल करें और x के लिए हल करें।

उदाहरण 6: ज़ेंडा की रियासत एक असामान्य मुद्रा प्रणाली का उपयोग करती है। 16 क्रोंखाइट्स एक ग्रोटनिक बनाने के लिए आवश्यक हैं और 12 ग्रोटनिक्स एक गज़ू बनाने के लिए। वर्तमान में, $1 को 8 ग्रोटनिक्स और 8 क्रोंखाइट्स के लिए विनिमय किया जा सकता है। एक आगंतुक जो ज़ेंडा से आया है, 100 गज़ू के बिल के लिए कितनी अमेरिकी मुद्रा का विनिमय कर सकता है, निकटतम सेंट पर? (क) $141.18 (ख) $85.00 (ग) $11.76 (घ) $70.83 (ङ) उपरोक्त में से कोई नहीं उत्तर: (क) $1 को 8 ग्रोटनिक्स और 8 क्रोंखाइट्स के लिए विनिमय किया जा सकता है, या समान रूप से, 8.5 ग्रोटनिक्स (8 क्रोंखाइट्स एक ग्रोटनिक के आधे के बराबर हैं)। 100 गज़ू 100 x 12 = 1,200 ग्रोटनिक्स के बराबर हैं। इसलिए, यदि D वह डॉलर है जिसे 100 गज़ू के बिल के लिए विनिमय किया जा सकता है, तो हम अनुपात स्थापित कर सकते हैं:

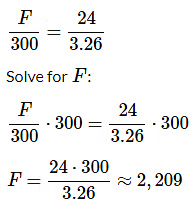
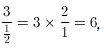
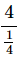
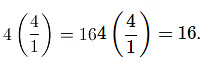
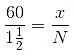
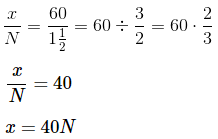
D के लिए हल करें:

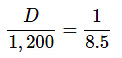
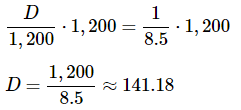
यानी, 100-गज़ू बिल को $141.18 में बदला जा सकता है।

उदाहरण 7: एक डिब्बे में लाल और नीले कबूतर हैं। लाल कबूतर चुनने की संभावना 1/3 है। डिब्बे में 30 नीले कबूतर हैं। कुल मिलाकर कितने कबूतर हैं? (क) 45 (ख) 50 (ग) 40 (घ) 60 (ङ) 90 उत्तर: (क) यदि 1/3 लाल हैं, तो 2/3 नीले हैं, और नीले कबूतरों की संख्या को इस प्रकार लिखा जा सकता है:

नीले कबूतरों की संख्या, 30, में लगाएँ और कुल कबूतरों के लिए हल करें।

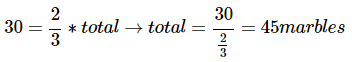
उदाहरण 8: एक निश्चित कक्षा में सभी छात्र या तो सॉफोमोर्स या जूनियर्स हैं। कक्षा में लड़कों और लड़कियों की संख्या समान है। लड़कियों में 3/7 सॉफोमोर्स हैं, और वहाँ 24 जूनियर लड़के हैं। यदि कक्षा में जूनियर लड़कों की संख्या कुल लड़कों की तुलना में उसी अनुपात में है जैसा सॉफोमोर्स लड़कियों की कुल लड़कियों के साथ है, तो कक्षा में कुल कितने छात्र हैं? (क) 96 (ख) 72 (ग) 56 (घ) 168 (ङ) 112 उत्तर: (ङ) यह प्रश्न जटिल लगता है लेकिन वास्तव में यह उतना सरल है जितना यह प्रतीत होता है। हमें बताया गया है कि कक्षा में लड़कों और लड़कियों की संख्या समान है और लड़कियों में 3/7 सॉफोमोर्स हैं। फिर हमें बताया गया है कि 24 लड़के जूनियर्स हैं, और वे कुल लड़कों का अनुपात सॉफोमोर्स लड़कियों के कुल लड़कियों के अनुपात के बराबर हैं। इसका मतलब है: जहाँ x कुल लड़कों की संख्या है। यदि हम जानते हैं कि कक्षा में लड़कों और लड़कियों की संख्या समान है, तो कक्षा में छात्रों की कुल संख्या = 112।

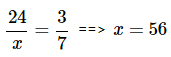
उदाहरण 9: निशिता के पास हार, कंगन, और अंगूठियों का अनुपात 7:5:4 है। यदि उसके पास कुल 64 आभूषण हैं, तो उसके पास कितने कंगन हैं? (क) 16 (ख) 20 (ग) 5 (घ) 28 (ङ) 32 उत्तर: (ख) 7x + 5x + 4x = 64, 16x = 64, x = 4, कंगन: 5x = 5(4) = 20

उदाहरण 10: पाँच अलग-अलग पिज़्ज़ा स्थान पाँच अलग-अलग विशेष पेशकश करते हैं। मान लेते हैं कि ये सभी पिज़्ज़ा समान मोटाई के हैं और सभी की गुणवत्ता समान है, तो निम्नलिखित में से सबसे अच्छा सौदा कौन सा है? (a) 10 इंच व्यास का गोल पिज़्ज़ा $5.99 में (b) 12 इंच व्यास का गोल पिज़्ज़ा $8.99 में (c) 12 इंच बाय 8 इंच का आयताकार पिज़्ज़ा $9.99 में (d) 9 इंच बाय 9 इंच का वर्गाकार पिज़्ज़ा $6.99 में (e) 10 इंच बाय 10 इंच का वर्गाकार पिज़्ज़ा $7.99 में। उत्तर: (a) चूंकि सभी पिज़्ज़ा समान मोटाई और गुणवत्ता के हैं, सबसे अच्छे सौदे का निर्धारण करने के लिए प्रत्येक का वर्ग इंच पर मूल्य निकालें। सबसे कम राशि सबसे अच्छे सौदे को दर्शाएगी।

एक गोल पिज़्ज़ा 10 इंच व्यास का $5.99 में: पिज़्ज़ा का क्षेत्र वर्ग इंच में है। प्रति वर्ग इंच की लागत: 5.99 ÷ 25π = 0.076 या 7.6 सेंट।

एक गोल पिज़्ज़ा 12 इंच व्यास का $8.99 में: पिज़्ज़ा का क्षेत्र वर्ग इंच में है। A = πr² = π⋅6² = 36π। प्रति वर्ग इंच की लागत: 8.99 ÷ 36π = 0.079 या 7.9 सेंट।

एक 9 इंच बाय 9 इंच का वर्गाकार पिज़्ज़ा $6.99 में: पिज़्ज़ा का क्षेत्र वर्ग इंच में है। 9⋅9 = 81। प्रति वर्ग इंच की लागत: 6.99 ÷ 81 = 0.086 या 8.6 सेंट।

एक 10 इंच बाय 10 इंच का वर्गाकार पिज़्ज़ा $7.99 में: पिज़्ज़ा का क्षेत्र वर्ग इंच में है। 10⋅10 = 100। प्रति वर्ग इंच की लागत: 7.99 ÷ 100 = 0.080 या 8.0 सेंट।

एक 12 इंच बाय 8 इंच का आयताकार पिज़्ज़ा $9.99 में: पिज़्ज़ा का क्षेत्र वर्ग इंच में है। 12⋅8 = 96। प्रति वर्ग इंच की लागत: 9.99 ÷ 96 = 0.104 या 10.4 सेंट।

10 इंच व्यास का गोल पिज़्ज़ा $5.99 में सबसे अच्छा सौदा है।

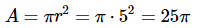
उदाहरण 11: यदि दो मित्रों A और B की उम्र का अनुपात 3 : 5 है और B और C का अनुपात 3 : 5 है और तीनों मित्रों की उम्र का योग 147 है, तो B की उम्र क्या है? (a) 15 वर्ष (b) 75 वर्ष (c) 49 वर्ष (d) 45 वर्ष (e) 27 वर्ष। उत्तर: (d)

दो दोस्तों A और B की उम्र का अनुपात = 3 : 5
दो दोस्तों B और C की उम्र का अनुपात = 3 : 5
A, B और C की उम्र का योग = A + B + C = 147 ... (i)

चरण 1: अनुपात को इस तरह व्यक्त करें कि B का मान दोनों अनुपातों में समान हो।
B के मान को दोनों अनुपातों में समान कैसे करें?
दोनों अनुपातों में B के मान को उनके LCM के रूप में पुनः लिखें।
पहले अनुपात को 3 से गुणा करें → A : B = 9 : 15
दूसरे अनुपात को 5 से गुणा करें → B : C = 15 : 25

चरण 2: A : B : C की गणना करें।
अब जब B का मान दोनों अनुपातों में समान है, तब A : B : C = 9 : 15 : 25

चरण 3: B की उम्र की गणना करें।
तो, यदि A की उम्र 9x वर्ष है, तो B की उम्र 15x और C की उम्र 25x होगी।
उनकी उम्र का योग 147 है।
तो, 9x + 15x + 25x = 147
49x = 147 या x = 3
B की उम्र = 15x = 15 × 3 = 45
B की उम्र = 45 वर्ष
विकल्प D सही उत्तर है।

उदाहरण 12: एक बॉक्स में x लाल गेंदें हैं, तीन गुना हरी गेंदें और लाल गेंदों की आधी नीली गेंदें हैं। यदि बॉक्स में कोई अन्य गेंदें नहीं हैं, तो निम्नलिखित में से बॉक्स में गेंदों की संख्या क्या हो सकती है?
(a) 22 (b) 44 (c) 54 (d) 33 (e) 24

लाल गेंदों की संख्या = x
हरी गेंदों की संख्या → लाल गेंदों की संख्या के तीन गुना = 3x
नीली गेंदों की संख्या → लाल गेंदों की संख्या की आधी = x/2
गेंदों की कुल संख्या = x + 3x + x/2 = 9x/2

गेंदों की कुल संख्या और लाल गेंदों की संख्या दोनों पूर्णांक हैं।
इसलिए, 9x/2 और x पूर्णांक हैं।
यदि 9x/2 एक पूर्णांक है, तो x एक सम संख्या होनी चाहिए।
पांच उत्तर विकल्पों में से चार सम हैं।
हमें उत्तर पर पहुँचने के लिए अतिरिक्त निष्कर्ष की आवश्यकता है।
किसी भी सम मान के लिए x, 9x/2 9 का गुणांक होगा।
इसलिए, गेंदों की कुल संख्या 9 का गुणांक होना चाहिए।
उत्तर विकल्पों में 9 का एकमात्र गुणांक 54 है।
बॉक्स में गेंदों की संख्या = 54

उदाहरण 13: यदि a, b, और c ऐसे संख्या हैं कि (a b) : (b c) : (c a) का अनुपात 15 : 11 : 12 है, तो

(a) मात्रा A बड़ी है (b) मात्रा B बड़ी है (c) दोनों मात्रा समान हैं (d) निर्धारित नहीं किया जा सकता

दी गई डेटा (a b) : (b c) : (c a) = 15 : 11 : 12। a और c की तुलना करने के लिए, इस अनुपात के पहले दो घटकों की तुलना करना पर्याप्त है। (a b) : (c b) = 15 : 11। चूंकि b दोनों घटकों में एक स्थायी है, हम उपरोक्त अनुपात को समीकृत करके a और c में से बड़े को खोज सकते हैं। हालांकि, चेतावनी यह है कि अनुपात a b : c b 15 : 11 है। या तो दोनों a और c सकारात्मक हैं या नकारात्मक हैं।

मामला 1: दोनों a और c सकारात्मक हैं

मान लें कि (a b) का मान 15x है, और (c b) का मान 11x है। यदि x सकारात्मक है, तो यह स्पष्ट है कि 15x > 11x। ∴ (a b) > (c b) मामले 1 के आधार पर, हम यह निष्कर्ष निकाल सकते हैं कि a > c।

मामला 2: दोनों a और c नकारात्मक हैं

मान लें कि (a b) का मान 15x है, और (c b) का मान 11x है। यदि x नकारात्मक है, तो यह स्पष्ट है कि 15x < 11x।="" ∴="" (a="" b)="" />< (c="" b)="" मामले="" 2="" के="" आधार="" पर,="" हम="" यह="" निष्कर्ष="" निकाल="" सकते="" हैं="" कि="" a="" />< c।="" />

चूंकि दोनों संभावनाएँ मौजूद हैं, हम प्रश्न में दी गई जानकारी के आधार पर यह निर्धारित नहीं कर सकते कि a या c में से कौन बड़ा है। सही उत्तर प्राप्त करने की कुंजी यह याद रखना है कि 15: 11 हमेशा दो मात्राओं के सकारात्मक होने का परिणाम नहीं हो सकता।