नोट्स: मापन | गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 1 - CTET & State TET PDF Download
मापन गणित में एक महत्वपूर्ण अवधारणा है, जो वस्तुओं और घटनाओं के गुणों को मापने से संबंधित है। यह केंद्रीय शिक्षक पात्रता परीक्षा (CTET) और राज्य स्तर की शिक्षक पात्रता परीक्षाओं (TETs) के लिए एक आवश्यक विषय है, क्योंकि यह इकाइयों, रूपांतरणों और वास्तविक दुनिया के अनुप्रयोगों को समझने की नींव रखता है।
मापन के प्रकार
- लंबाई: दो बिंदुओं के बीच की दूरी। इकाइयां मीटर (m), सेंटीमीटर (cm) और किलोमीटर (km) हैं।
- भार: किसी वस्तु में पदार्थ की मात्रा। इकाइयां ग्राम (g) और किलोग्राम (kg) हैं।
- क्षमता: किसी कंटेनर में कितनी मात्रा समाहित हो सकती है। इकाइयां मिलीलीटर (ml) और लीटर (l) हैं।
- समय: घटनाओं के बीच का अंतराल। इकाइयां सेकंड (s), मिनट (min), घंटे (h), दिन, सप्ताह, महीने और वर्ष हैं।
- क्षेत्रफल: किसी आकृति के भीतर का स्थान। इकाइयां वर्ग मीटर (m²) और वर्ग सेंटीमीटर (cm²) हैं।
- आयतन: किसी वस्तु द्वारा घेरित स्थान। इकाइयां घन मीटर (m³) और घन सेंटीमीटर (cm³) हैं।
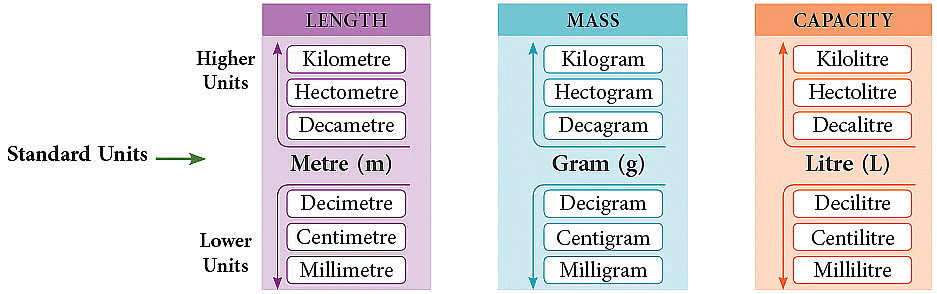
मापन की इकाइयाँ
- मीटर प्रणाली एक मापने की विधि है, जो 10 के गुणांक का उपयोग करती है।
- यह लंबाई (मीटर), वजन (ग्राम) और क्षमता (लीटर) के लिए मानक इकाइयाँ प्रदान करती है।
- इन मानक इकाइयों का एक दृश्य प्रतिनिधित्व प्रदर्शित किया गया है।
- कभी-कभी ये इकाइयाँ बहुत छोटी या बहुत बड़ी होती हैं, जिसको मापने के लिए हमें आवश्यक होता है।
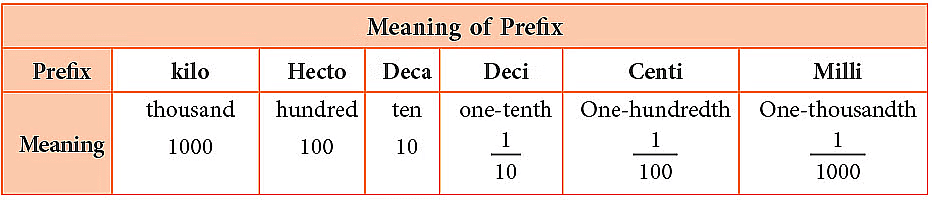
- इसे ठीक करने के लिए, हम मानक इकाइयों के साथ उपसर्गों का उपयोग करते हैं, ताकि बड़ी या छोटी इकाइयाँ बनाई जा सकें।
- उदाहरण के लिए, "किलो" का अर्थ है 1000, इसलिए एक किलोमीटर 1000 मीटर है।
- और "मिली" का अर्थ है 1/1000, इसलिए एक मिलीलीटर 1/1000 लीटर है, जो वास्तव में बहुत छोटा है।
- यह हमें लंबी दूरियों, छोटे द्रव की मात्रा, या बड़े वजन को मापने में आसानी प्रदान करता है।
लंबाई का मापन

लंबाई मापने के लिए विभिन्न इकाइयाँ उपयोग की जाती हैं, जैसे कि किलोमीटर, मीटर, सेंटीमीटर, और मिलीमीटर।
- किलोमीटर बहुत लंबी दूरियों के लिए होता है, जैसे कि शहरों के बीच।
- मीटर मानक इकाई है, जिसका उपयोग कमरे की लंबाई या व्यक्ति की ऊँचाई मापने के लिए किया जाता है।
- सेंटीमीटर छोटे मापों के लिए उपयोग किया जाता है, जैसे कि एक किताब की चौड़ाई।
- मिलीमीटर और भी छोटे मापों के लिए होता है, जैसे कि एक सिक्के की मोटाई।

नीचे दिया गया चार्ट मेट्रिक प्रणाली में लंबाई की इकाइयों को मीटर को संदर्भ इकाई के रूप में दिखाता है। यह दिखाता है कि मेट्रिक प्रणाली दशमलव प्रणाली के समान है।

विभिन्न लंबाई की इकाइयों के बीच संबंध
यह चार्ट आपको बड़ी इकाइयों को छोटी इकाइयों में और छोटी इकाइयों को बड़ी इकाइयों में परिवर्तित करने में मदद करेगा।
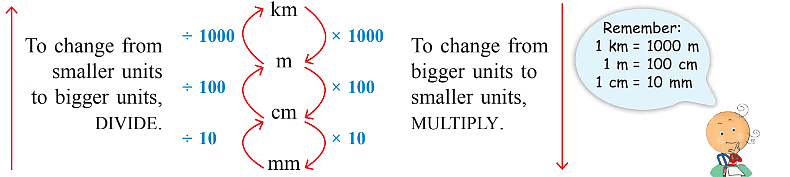
निम्नलिखित चित्र दिखाता है कि इन परिवर्तनों को कैसे किया जाए।

नियम:
- बाएँ से दाएँ बढ़ते समय, आप प्रत्येक चरण में 10 से गुणा करते हैं। एक कदम दाएँ बढ़ें, 10 से गुणा करें, दो कदम दाएँ बढ़ें, 10 × 10 = 100 से गुणा करें और इसी तरह आगे बढ़ें।
- दाएँ से बाएँ बढ़ते समय, आप प्रत्येक चरण में 10 से विभाजित करते हैं। एक कदम बाएँ बढ़ें, 10 से विभाजित करें, दो कदम बाएँ बढ़ें, 100 से विभाजित करें और इसी तरह आगे बढ़ें।
हल किए गए उदाहरण
उदाहरण 1: निम्नलिखित बड़ी इकाइयों को छोटी इकाइयों में परिवर्तित करें।
- 3 किमी = (3 × 1000) मीटर = 3000 मीटर
- 8 हेक्टोमीटर = (8 × 100) मीटर = 800 मीटर
- 5 मीटर = (5 × 100) सेंटीमीटर = 500 सेंटीमीटर
- 1.03 मीटर = (1.03 × 1000) मिलीमीटर = 1030 मिलीमीटर
उदाहरण 2: निम्नलिखित छोटी इकाइयों को बड़ी इकाइयों में परिवर्तित करें।
- 8400 मीटर = (8400 ÷ 1000) किमी = 8.4 किमी
- 370 मीटर = (370 ÷ 100) हेक्टोमीटर = 3.7 हेक्टोमीटर
- 2000 मिलीमीटर = (2000 ÷ 1000) मीटर = 2 मीटर
- 73 सेंटीमीटर = (73 ÷ 100) मीटर = 0.73 मीटर
उदाहरण 3: निर्देशानुसार परिवर्तित करें। (क) 60 मिलीमीटर को सेंटीमीटर में (ख) 720 डैम को किमी में (ग) 85 हेक्टोमीटर को किमी में (घ) 7340 डेम को हेक्टोमीटर में (ङ) 12000 सेंटीमीटर को डैम में
हल: (a) 60 मिमी = (60 ÷ 10) सेमी = 6 सेमी। सेमी मिमी से एक कदम बाईं ओर है, इसलिए 10 से विभाजित करें। (b) 720 डैम = (720 ÷ 100) किमी = 7.2 किमी। किमी डैम से दो कदम बाईं ओर है, इसलिए 100 से विभाजित करें। (c) 85 एचएम = (85 ÷ 10) किमी = 8.5 किमी। किमी एचएम से एक कदम बाईं ओर है, इसलिए 10 से विभाजित करें। (d) 7340 डेम = (7340 ÷ 1000) एचएम = 7.340 एचएम। एचएम डेम से तीन कदम बाईं ओर है, इसलिए 1000 से विभाजित करें। (e) 12000 सेमी = (12000 ÷ 1000) डैम = 12 डैम। डैम सेमी से तीन कदम बाईं ओर है, इसलिए 1000 से विभाजित करें।
लंबाई व्यक्त करने के लिए दशमलव का उपयोग
- दशमलव हमें छोटी इकाइयों का उपयोग करके लंबाई व्यक्त करने में मदद करते हैं।
- उदाहरण के लिए, यदि रिनी के पिता 7 किलोमीटर और 500 मीटर यात्रा करते हैं, तो हम इसे 7500 मीटर के रूप में लिख सकते हैं।
- दशमलव का उपयोग करते हुए, हम इसे 7.500 किलोमीटर के रूप में भी लिख सकते हैं।
- इस प्रकार, 7 किलोमीटर और 500 मीटर दशमलव के उपयोग के साथ 7.500 किलोमीटर के समान है।

उदाहरण 1: सोमवार को 2.1 सेमी वर्षा हुई। यह मिमी में कितना है? हल: 2.1 × 10 = 21 मिमी। सोमवार को वर्षा 21 मिमी थी।
उदाहरण 2: मेरी माँ की ऊँचाई 153 सेमी है। यह मीटर में कितना होगा? हल: 153 ÷ 100 = 1.53 मी। मेरी माँ की ऊँचाई 1.53 मी है।
उदाहरण 3: एक साइकिल का पहिया 1 चक्र में 2 मीटर की दूरी तय करता है। 600 चक्रों में यह कितनी दूरी तय करेगा? अपना उत्तर किमी में लिखें। हल: 600 चक्रों में तय की गई दूरी = 2 × 600 = 1200 मीटर। 1200 मीटर ÷ 1000 मीटर = 1.2 किमी। पहिया 600 चक्रों में 1.2 किमी की दूरी तय करेगा।
भार (वजन) का मापन
- किसी वस्तु में पदार्थ की मात्रा उसका भार होती है।
- हम वजन मापने के लिए विभिन्न इकाइयाँ उपयोग करते हैं, जैसे किलोग्राम, ग्राम, और मिलीग्राम।
- किलोग्राम भारी चीजों के लिए होते हैं, जैसे लोग या आटे के थैले।
- ग्राम हल्की चीजों के लिए मानक इकाई है, जैसे सेब या पेंसिल।
- मिलीग्राम बहुत हल्की चीजों के लिए होते हैं, जैसे नमक के छोटे दाने या औषधि की खुराक।
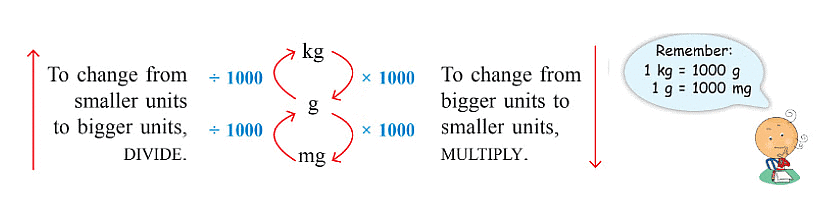
- नीचे दिया गया चार्ट ग्राम को संदर्भ इकाई के रूप में लेकर मीट्रिक प्रणाली में भार की इकाइयों को दर्शाता है।

भार की विभिन्न इकाइयों के बीच संबंध
विभिन्न द्रव्यमान इकाइयों के बीच संबंध

यह चार्ट आपको बड़ी इकाइयों को छोटी इकाइयों में और छोटी इकाइयों को बड़ी इकाइयों में परिवर्तित करने में मदद करेगा।
द्रव्यमान (वजन) व्यक्त करने के लिए दशमलवों का उपयोग
- दशमलव हमें वजन को बड़ी इकाइयों का उपयोग करके दिखाने में मदद करते हैं। उदाहरण के लिए, यदि रिनी की माँ 1 किलोग्राम और 750 ग्राम टमाटर खरीदती हैं, तो हम इसे 1750 ग्राम के रूप में लिख सकते हैं।
- दशमलव का उपयोग करते हुए, हम इसे 1.750 किलोग्राम के रूप में भी लिख सकते हैं। इसलिए, 1 किलोग्राम और 750 ग्राम 1.750 किलोग्राम के समान है।

उदाहरण 1: विभिन्न इकाइयों को ग्राम में परिवर्तित करना और इसके विपरीत।
- (i) 24 किलोग्राम = (24 × 1000) ग्राम = 24000 ग्राम
- (ii) 1.217 ग्राम = (1.217 × 1000) मिलीग्राम = 1217 मिलीग्राम
- (iii) 3200 मिलीग्राम = (3200 ÷ 1000) ग्राम = 3.2 ग्राम
- (iv) 315 सेंटीग्राम = (315 ÷ 100) ग्राम = 3.15 ग्राम
उदाहरण 2: इकाइयों के बीच परिवर्तन
- (i) 14 मिलीग्राम = (14 ÷ 10) सेंटीग्राम = 1.4 सेंटीग्राम
- (ii) 300 डेसिग्राम = (300 ÷ 100) डेकाग्राम = 3 डेकाग्राम


(iii) 2417 सेंटीग्राम = (2417 ÷ 1000) डेकाग्राम = 2.417 डेकाग्राम

(iv) 38 किलोग्राम = (38 × 100) डेकाग्राम = 3800 डेकाग्राम

(v) 23.7 डेसिग्राम = (23.7 × 10) सेंटीग्राम = 237 सेंटीग्राम

(vi) 4 हेक्टोग्राम = (4 × 1000) डेसिग्राम = 4000 डेसिग्राम

उदाहरण 3: एक सेबों की टोकरी का वजन 2.5 किलोग्राम है। यह ग्राम में कितना है?
हल: 2.5 × 1000 = 2500 ग्राम। सेबों की टोकरी का वजन 2500 ग्राम है।
क्षमता का मापन
- हम यह मापने के लिए विभिन्न इकाइयों का उपयोग करते हैं कि कोई चीज कितना तरल रख सकती है, जैसे कि लीटर और मिलीलीटर।
- लीटर तरल मापने के लिए मानक इकाई है, जैसे कि एक जग में कितना पानी है।
- मिलीलीटर लीटर से छोटी होती है और इसका उपयोग तरल की छोटी मात्रा मापने के लिए किया जाता है, जैसे कि सिरिंज में दवाई।
नीचे दिया गया चार्ट मेट्रिक प्रणाली में क्षमता की इकाइयों को दर्शाता है, जिसमें लीटर संदर्भ इकाई के रूप में है।
विभिन्न क्षमता इकाइयों के बीच संबंध
दशमलवों का उपयोग करके क्षमता व्यक्त करना
- दशमलव हमें दिखाने में मदद करते हैं कि किसी चीज़ में कितना तरल पदार्थ हो सकता है, बड़े इकाइयों का उपयोग करके।
- उदाहरण के लिए, यदि रिनी के भाई ने 1 लीटर और 200 मिलीलीटर नींबू पानी बनाया, तो हम इसे 1200 मिलीलीटर के रूप में लिख सकते हैं।
- दशमलवों का उपयोग करके, हम इसे 1.200 लीटर के रूप में भी लिख सकते हैं।
- इसलिए, 1 लीटर और 200 मिलीलीटर का वही अर्थ है जब हम दशमलव का उपयोग करते हैं।
हल किए गए उदाहरण
उदाहरण 1: विभिन्न इकाइयों को लीटर में और लीटर को विभिन्न इकाइयों में परिवर्तित करना
- (i) 2.3 kL = (2.3 × 1000) L = 2300 L
- (ii) 1.8 cL = (1.8 ÷ 100) L = 0.018 L
- (iii) 64 hL = (64 × 100) L = 6400 L
- (iv) 600 L = (600 ÷ 100) hL = 6 hL
- (v) 7315 mL = (7315 ÷ 1000) L = 7.315 L
- (vi) 11.9 L = (11.9 × 1000) mL = 11900 mL
उदाहरण 2: इकाइयों के बीच परिवर्तनों का उदाहरण
- (i) 25 hL = (25 × 10) daL = 250 daL
- (ii) 13.8 dL = (13.8 × 100) mL = 1380 mL
- (iii) 500 daL = (500 ÷ 100) kL = 5 kL
- (iv) 3.117 hL = (3.117 × 1000) dL = 3117 dL
मेट्रिक मापों पर चार मूल ऑपरेशन्स: जोड़ना और घटाना
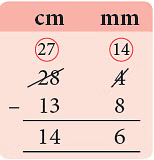
उदाहरण 1: रितु ने 15 सेमी 4 मिमी लंबाई का एक रेखा खींचा। फिर, उसने इसका एक भाग मिटा दिया। बची हुई रेखा की लंबाई 7 सेमी 6 मिमी थी। मिटाए गए रेखा खंड की लंबाई मिमी में क्या है?
हल: शुरुआत में रेखा खंड की लंबाई = 15 सेमी 4 मिमी
मिटाने के बाद बची रेखा खंड की लंबाई = 7 सेमी 6 मिमी
मिटाए गए रेखा खंड की लंबाई = 15 सेमी 4 मिमी - 7 सेमी 6 मिमी = 7 सेमी 8 मिमी
जोड़ना और घटाना
उदाहरण 2: जोड़ें:
- (a) 3 सेमी 4 मिमी और 9 सेमी 8 मिमी
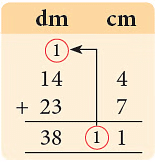
- (b) 14 डेम 4 सेंटीमीटर और 23 डेम 7 सेंटीमीटर
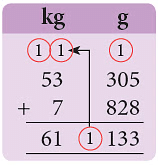
- (c) 53 किलोग्राम 305 ग्राम और 7 किलोग्राम 828 ग्राम
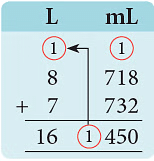
- (d) 8 लीटर 718 मिलीलीटर और 7 लीटर 732 मिलीलीटर


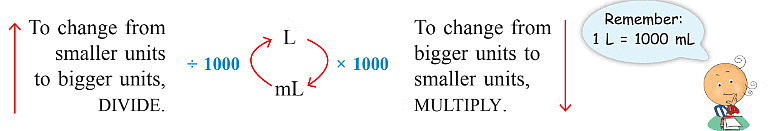




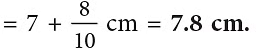

हल: (क) 12 मिमी = 10 मिमी 2 मिमी = 1 सेमी 2 मिमी = 13 सेमी 2 मिमी = 13.2 सेमी। (ख) 11 सेमी = 10 सेमी 1 सेमी = 1 डेम 1 सेमी = 38 डेम 1 सेमी = 38.1 डेम। (ग) 1133 ग्राम = 1000 ग्राम 133 ग्राम = 1 किलोग्राम 133 ग्राम = 61 किलोग्राम 133 ग्राम = 61.133 किलोग्राम। (घ) 1450 मिलीलीटर = 1000 मिलीलीटर 450 मिलीलीटर = 1 लीटर 450 मिलीलीटर = 16 लीटर 450 मिलीलीटर = 16.450 लीटर।
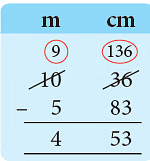
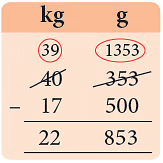
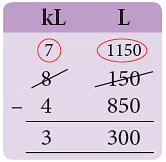
उदाहरण 3: घटाएँ: (क) 10 मी 36 सेमी - 5 मी 83 सेमी (ख) 28 सेमी 4 मिमी - 13 सेमी 8 मिमी (ग) 40 किलोग्राम 353 ग्राम - 17 किलोग्राम 500 ग्राम (घ) 8 किलोलिटर 150 लीटर - 4 किलोलिटर 850 लीटर
हल: (क) 36 सेमी < 83="" सेमी="" 1="" मी="100" सेमी="" उधार="" लें="" 100="" सेमी="" 36="" सेमी="136" सेमी="4.53" मी।="" (ख)="" 4="" मिमी="" />< 8="" मिमी="" 1="" सेमी="10" मिमी="" उधार="" लें="" 10="" मिमी="" 4="" मिमी="14" मिमी="14.6" सेमी।="" (ग)="" 353="" ग्राम="" />< 500="" ग्राम="" 1="" किलोग्राम="1000" ग्राम="" उधार="" लें="" 1000="" ग्राम="" 353="" ग्राम="1353" ग्राम="22.853" किलोग्राम।="" (घ)="" 150="" लीटर="" />< 850="" लीटर="" 1="" किलोलिटर="1000" लीटर="" उधार="" लें="" 1000="" लीटर="" 150="" लीटर="1150" लीटर="3.300" />
गुणन
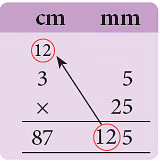
संख्याओं को इकाई के अनुसार कॉलम में व्यवस्थित करें और फिर जैसे आप पूर्ण संख्याओं को गुणा करते हैं, वैसे गुणा करें। उदाहरण 4: 25 किताबों के एक ढेर की ऊँचाई ज्ञात करें, यदि प्रत्येक किताब की मोटाई 3 सेमी 5 मिमी है। हल: 1 किताब की मोटाई = 3 सेमी 5 मिमी = 3.5 सेमी 25 किताबों की ऊँचाई = 3.5 सेमी × 25 = 87.5 सेमी इस प्रकार, 25 किताबों के ढेर की ऊँचाई = 87.5 सेमी।
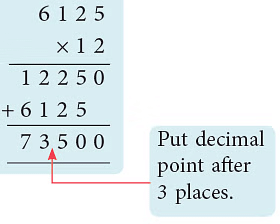
उदाहरण 5: फलों से भरा एक कार्टन का वजन 6 किलोग्राम 125 ग्राम है। 12 ऐसे कार्टनों का वजन किलोग्राम में क्या है? हल: एक कार्टन का वजन = 6 किलोग्राम 125 ग्राम = 6.125 किलोग्राम ∴ 12 कार्टनों का वजन = (6.125 × 12) किलोग्राम = 73.500 किलोग्राम = 73 किलोग्राम 500 ग्राम।
भाग
भाग में भी संख्याओं को इकाई के अनुसार कॉलम में व्यवस्थित करें और फिर जैसे पूर्ण संख्याओं को भाग करते हैं, वैसे भाग करें।
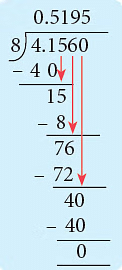
उदाहरण 6: रीना ने 4 लीटर 156 मिलीलीटर संतरे का रस तैयार किया। इसे 8 बच्चों में समान रूप से वितरित करें। प्रत्येक बच्चे को कितने मिलीलीटर संतरे का रस मिलता है? हल: रीना द्वारा तैयार किया गया रस = 4 लीटर 156 मिलीलीटर = 4.156 लीटर जब 8 बच्चों में वितरित किया जाता है, तो प्रत्येक बच्चे को मिलने वाला रस = (4.156 ÷ 8) लीटर = 0.51 95 लीटर = 519.5 मिलीलीटर।
उदाहरण 7: 5 बोतलों में 1.2 लीटर सोडा है, तो मैं 150 मील के कितने गिलास भर सकता हूँ? हल: 5 बोतलों में कुल सोडा = 1.2 L × 5 = 6.0 = 6 L चूंकि 1 L = 1000 mL कुल सोडा = 6 L = 6 × 1000 = 6000 mL 150 mL के गिलासों की संख्या जो भरे जा सकते हैं = 6000 mL ÷ 150 mL = 40 इस प्रकार, 6 L सोडे के साथ, मैं 150 mL के 40 गिलास भर सकता हूँ।
माप में आकलन आप हमेशा माप में सटीक नहीं रह सकते। हमारे दैनिक जीवन में, हम माप का आकलन करते हैं। माप को सही ढंग से आकलन करने के लिए, आपको यह समझना चाहिए कि सामान्य चीजों को प्रचलित माप की इकाइयों के साथ कैसे संबंधित किया जाए।
- लंबी लंबाई या दूरी के लिए, हम किलोमीटर (km) का उपयोग करते हैं।
- भारत की लंबाई = 3214 km
- भारत की चौड़ाई = 2933 km
- मध्यम लंबाई के लिए, हम मीटर (m) का उपयोग करते हैं।
- आपके खाने की मेज़ की लंबाई।
- छोटी लंबाई के लिए, हम सेंटीमीटर (cm) का उपयोग करते हैं।
- एक छोटे स्केल की लंबाई = 15 cm।
- बहुत छोटी लंबाई के लिए, हम मिलीमीटर (mm) का उपयोग करते हैं।
- आपकी पेंसिल का टिप = 2 mm।
- बहुत बड़े द्रव्यमान के लिए, हम टन (t) और क्विंटल (q) का उपयोग करते हैं।
- ट्रक = 4 टन
- चावल का बोरा = 1 क्विंटल।
- मध्यम द्रव्यमान के लिए, हम किलोग्राम (kg) का उपयोग करते हैं।
- आपके स्कूल बैग का वजन = 5 kg।
- छोटे द्रव्यमान के लिए, हम ग्राम (g) का उपयोग करते हैं।
- एक संतरा लगभग 100 g है।
- बहुत छोटे द्रव्यमान के लिए, हम मिलीग्राम (mg) का उपयोग करते हैं।
- एक चम्मच नमक = 5 mg।
- बड़े क्षमता के लिए, हम किलोलिटर का उपयोग करते हैं।
- एक स्विमिंग पूल की क्षमता = 600 kL।
- मध्यम क्षमता के लिए, हम लीटर का उपयोग करते हैं।
- एक स्नान बाल्टी = 20 L।
- छोटी क्षमता के लिए, हम मिलीलीटर का उपयोग करते हैं।
- एक दवा की बोतल = 200 mL।
मात्राओं के अंश निकालना

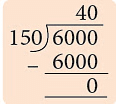






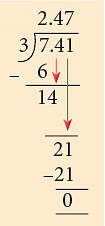
उदाहरण 8: एक टोकरी में 3 किलोग्राम 705 ग्राम आम हैं। 23 आम श्री भसीन द्वारा खा लिए गए। उनकी बेटी लता को शेष आमों में से 25 आम मिलते हैं। उसका हिस्सा कितने ग्राम है?
हल: आमों का कुल वजन = 3 किलोग्राम 705 ग्राम
श्री भसीन द्वारा खाए गए आम
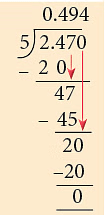
शेष आम = 3.705 किलोग्राम – 2.47 किलोग्राम = 1.235 किलोग्राम
लता द्वारा खाए गए आम = (0.494 × 1000) ग्राम = 494 ग्राम
तो, लता ने 494 ग्राम आम खाए।
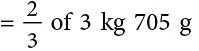
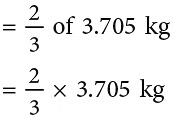
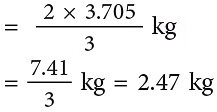
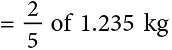
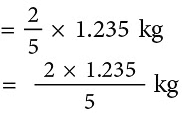
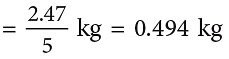
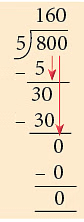
उदाहरण 9: अंशुल के पास 45 किलोग्राम वेफर्स थे। उसने सभी वेफर्स को 5 छोटे पैकेट में समान रूप से पैक किया। प्रत्येक पैकेट में कितने ग्राम वेफर्स थे?
हल: अंशुल के पास कुल वेफर्स = 4 / 5 किलोग्राम = 800 ग्राम
800 ग्राम वेफर्स 5 छोटे पैकेट में भरे गए।
∴ एक पैकेट में वेफर्स = 800 ÷ 5 = 800 / 5 = 160 ग्राम
तो, प्रत्येक पैकेट में 160 ग्राम वेफर्स हैं।
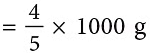
उदाहरण 15: माधुरी ने 20 सेंटीमीटर 5 मिलीमीटर लंबा एक रेखा खींचा। उसने गलती से इसका 2 / 5 हिस्सा मिटा दिया। शेष रेखा की लंबाई कितनी सेंटीमीटर है?
हल: खींची गई रेखा की लंबाई = 20 सेंटीमीटर 5 मिलीमीटर = 20.5 सेंटीमीटर
मिटाए गए रेखा का लंबाई = 2 / 5 का 20.5 सेंटीमीटर = (2 × 4.1) सेंटीमीटर = 8.2 सेंटीमीटर
शेष रेखा की लंबाई = 20.5 सेंटीमीटर – 8.2 सेंटीमीटर = 12.3 सेंटीमीटर।
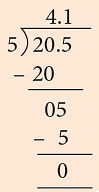
|
29 videos|73 docs|72 tests
|
















