त्रिकोणों की संगति और समानता | Mathematics for RRB NTPC (Hindi) - RRB NTPC/ASM/CA/TA PDF Download

ज्यामिति SSC मात्रात्मक कौशल में एक महत्वपूर्ण विषय है, जो आकृतियों और आकारों पर केंद्रित है। इस क्षेत्र में उत्कृष्टता प्राप्त करने के लिए, मूलभूत सिद्धांतों, प्रमेयों और व्यावहारिक अनुप्रयोगों में महारत हासिल करना आवश्यक है। इस दस्तावेज़ में हम त्रिकोणों के बीच समानताओं और समानता पर चर्चा करेंगे, जो ज्यामिति का एक मूलभूत भाग है।

SSC के लिए त्रिकोणों की समानता और समानता

• दो त्रिकोणों को आकार और आकार में समान कहा जाता है जब उन्हें संगत कहा जाता है। इसका अर्थ है कि यदि दो त्रिकोणों की भुजाएँ और कोण मेल खाते हैं, तो वे संगत हैं।
• दो त्रिकोणों को समान कहा जाता है यदि उनके आकार समान हैं। इसका तात्पर्य है कि यदि कोण मेल खाते हैं और भुजाएँ अनुपात में हैं, तो त्रिकोण समान हैं।

CPCTC: संगत त्रिकोणों के संबंधित भाग संगत होते हैं।

त्रिकोणों की संगति के लिए शर्तें

1. SSS (भुजा-भुजा-भुजा):

संबंधित भुजाएँ समान होती हैं।

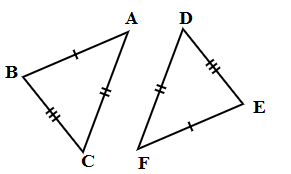
△ABC और △DEF में,

AB = FE, BC = ED और DF = CA

अतः △ABC ≅ △FED

2. SAS (भुजा-कोण-भुजा):

दो संबंधित भुजाएँ और उनके बीच का संबंधित कोण समान होता है।

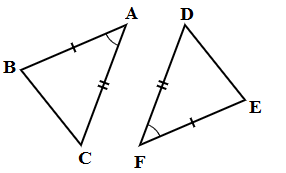
AB = FE, DF = CA और ∠A = ∠F

3. AAS (कोण-कोण-भुजा):

दो संबंधित कोण और उनके बीच का संबंधित भुजा समान होता है।

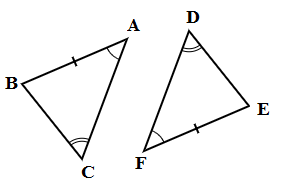
AB = FE, ∠C = ∠D और ∠A = ∠F

4. ASA (कोण-भुजा-कोण):

दो संबंधित कोण और उनके बीच का संबंधित भुजा समान होता है।

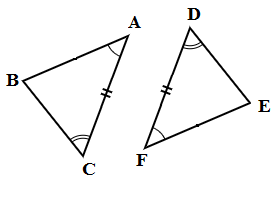
AC = FD, ∠C = ∠D और ∠A = ∠F

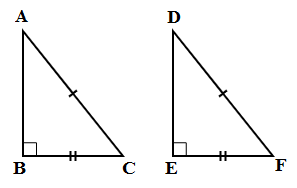
5. RHS (सही-हाइपोटेन्यूज-भुजा):

दो सही त्रिकोणों में हाइपोटेन्यूज और एक जोड़ी संबंधित कोण समान होते हैं।

∠B = ∠E = 90⁰, AC = DF और BC = EF

इसलिए △ABC ≅ △DEF

त्रिकोणों की समानता की शर्तें

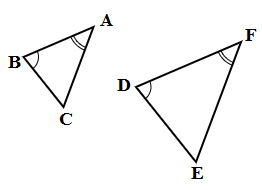
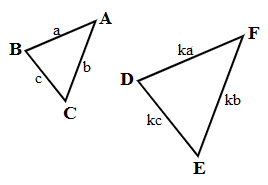
• AA (कोण-कोण): दो जोड़े समकोण बराबर हैं। △ABC और △FDE समान हैं।
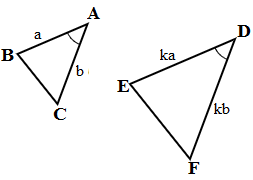
• SAS (पक्ष-कोण-पक्ष): दो जोड़े समपक्ष आनुपातिक हैं और उनके बीच का कोण बराबर है। △ABC और △DEF समान हैं।
• SSS (पक्ष-पक्ष-पक्ष): समपक्ष आनुपातिक हैं। AB/FD = BC/DE = AC/FE। △ABC और △FDE समान हैं।

नोट: यदि दो त्रिकोण समान हैं तो,

• दोनों त्रिकोणों के क्षेत्रफल का अनुपात = समपक्षों के वर्गों का अनुपात
• दोनों त्रिकोणों के पक्षों का अनुपात = उनके ऊँचाइयों/उचाई का अनुपात = उनके मध्याओं का अनुपात = उनके कोण बिसेक्टर का अनुपात = उनके अंतःकेंद्रों/परिकेंद्रों का अनुपात = उनके परिमाप का अनुपात

उपरोक्त शर्तें SSC परीक्षाओं के लिए त्रिकोणों की समानता और समरूपता की तैयारी की रीढ़ हैं। इन्हें सीखना आवश्यक है!

आइए, SSC परीक्षाओं के लिए त्रिकोणों की समरूपता और समानता पर कुछ महत्वपूर्ण प्रमेयों पर नज़र डालते हैं।

SSC के लिए त्रिकोणों की समरूपता और समानता: कुछ महत्वपूर्ण प्रमेय

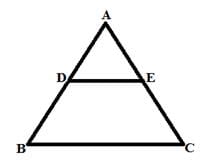
• मूल आनुपात प्रमेय: एक रेखा जो त्रिकोण के एक पक्ष के समानांतर हो, अन्य दो पक्षों को समान अनुपात में विभाजित करती है। यदि DE ││ BC तो, AD/DB = AE/EC
• उदाहरण: चतुर्भुज DECB का क्षेत्रफल 180 cm² है और DE AC को अनुपात 2:5 में विभाजित करता है। यदि DE ││ BC, तो △ADE का क्षेत्रफल क्या है?
• a) 16 cm² b) 32 cm² c) 40 cm² d) 20 cm²

उत्तर: a

हल: AE/EC = 2/5 (DE AC को अनुपात 2:5 में विभाजित करता है) AE/EC = AD/DB (मूल आनुपात प्रमेय) => AE/EC = AD/AB = 2/7 और ∠DAE = ∠BAC => △ADE और △ABC समान हैं। (SAS समानता नियम द्वारा)

△ADE का क्षेत्रफल / △ABC का क्षेत्रफल = (2/7)² = 4/49

मान लीजिए △ADE का क्षेत्रफल = 4x तो, △ABC का क्षेत्रफल = 49x

△ABC का क्षेत्रफल = △ADE का क्षेत्रफल + चतुर्भुज DCEB का क्षेत्रफल

49x = 4x + 180

45x = 180

x = 4

△ADE का क्षेत्रफल = 4x = 16 cm²

• कोण बिसेक्टर प्रमेय: कोण बिसेक्टर पक्ष को शेष दो पक्षों के अनुपात में विभाजित करता है। यदि AD ∠A को बिसेक्ट करता है तो, BD/DC = AB/AC
• उदाहरण: यदि AD ∠BAC को बिसेक्ट करता है और AD BC को अनुपात 1:1 में विभाजित करता है, तो △ABC के क्षेत्रफल का अनुपात △ABD के क्षेत्रफल के साथ क्या है?
• a) 3:1 b) 4:1 c) 3:2 d) 2:1

उत्तर: d

हल: BD/DC = AB/AC = 1 => AB = AC और BD = DC

साथ ही, AD = AD (सामान्य पक्ष)

△ABD ≅ △ACD (SSS समरूपता नियम द्वारा)

△ABC का क्षेत्रफल = △ABD का क्षेत्रफल + △ACD का क्षेत्रफल = 2 × △ABD का क्षेत्रफल (क्योंकि समरूप त्रिकोणों का क्षेत्रफल समान होता है)

आवश्यक अनुपात = 2:1

नोट: यदि दो त्रिकोण समान हैं तो,

SSC के लिए त्रिकोणों की संगति और समानता: कुछ महत्वपूर्ण प्रमेय

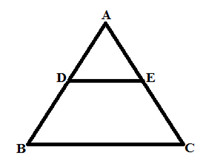
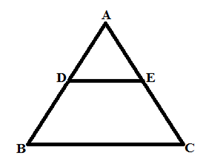
1. मूल आनुपातिकता प्रमेय: एक रेखा जो त्रिकोण की एक भुजा के समांतर है, अन्य दो भुजाओं को समान अनुपात में विभाजित करती है।

यदि DE ││ BC है, तो AD/DB = AE/EC

उदाहरण: चतुर्भुज DECB का क्षेत्रफल 180 cm² है और DE, AC को 2:5 के अनुपात में विभाजित करता है। यदि DE ││ BC है, तो △ADE का क्षेत्रफल क्या है?

• a) 16 cm²
• b) 32 cm²
• c) 40 cm²
• d) 20 cm²

उत्तर: a

समाधान: AE/EC = 2/5 (DE, AC को 2:5 के अनुपात में विभाजित करता है)

AE/EC = AD/DB (मूल आनुपातिकता प्रमेय)

=> AE/EC = AD/AB = 2/7 और ∠DAE = ∠BAC

=> △ADE और △ABC समान हैं। (SAS समानता नियम द्वारा)

△ADE का क्षेत्रफल / △ABC का क्षेत्रफल = (2/7)² = 4/49

मान लें △ADE का क्षेत्रफल = 4x, तो △ABC का क्षेत्रफल = 49x

△ABC का क्षेत्रफल = △ADE का क्षेत्रफल + चतुर्भुज DCEB का क्षेत्रफल

49x = 4x + 180

45x = 180

x = 4

△ADE का क्षेत्रफल = 4x = 16 cm²

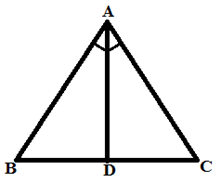
2. कोण द्विभाजक प्रमेय: कोण द्विभाजक उस भुजा को शेष दो भुजाओं के अनुपात में विभाजित करता है।

यदि AD ∠A को द्विभाजित करता है, तो BD/DC = AB/AC

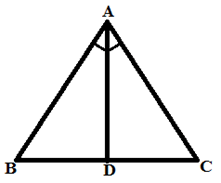
उदाहरण: यदि AD ∠BAC को द्विभाजित करता है और AD, BC को 1:1 के अनुपात में विभाजित करता है, तो △ABC के क्षेत्रफल का अनुपात △ABD के क्षेत्रफल के साथ क्या होगा?

• a) 3:1
• b) 4:1
• c) 3:2
• d) 2:1

उत्तर: d

समाधान: BD/DC = AB/AC = 1

=> AB = AC और BD = DC

साथ ही, AD = AD (समान भुजा)

△ABD ≅ △ACD (SSS संगति नियम द्वारा)

△ABC का क्षेत्रफल = △ABD का क्षेत्रफल + △ACD का क्षेत्रफल = 2 × △ABD का क्षेत्रफल (क्योंकि संगत त्रिकोणों का क्षेत्रफल समान होता है)

आवश्यक अनुपात: 2:1