|
A Quadratic Equation is a polynomial equation of degree 2, typically in the form ax² + bx + c = 0, where a, b, and c are constants and a ≠ 0. |
Card: 2 / 22 |
|
The quadratic formula, given by
|
Card: 4 / 22 |
|
Factoring the equation gives (x - 2)(x - 3) = 0. Setting each factor to zero gives the solutions: x = 2 and x = 3. |
Card: 6 / 22 |
|
The discriminant, calculated as D = b² - 4ac, indicates the nature of the roots: |
Card: 8 / 22 |
|
Given the quadratic equation 2x² + 4x + 2 = 0, use the quadratic formula to find the solutions. Hint: Identify a, b, and c first. |
Card: 9 / 22 |
|
Here, a = 2, b = 4, and c = 2. The discriminant is |
Card: 10 / 22 |
 Unlock all Flashcards with EduRev Infinity Plan Starting from @ ₹99 only
|
|
The vertex form of a quadratic equation is y = a(x - h)² + k, where (h, k) is the vertex of the parabola. It is derived by completing the square on the standard form ax² + bx + c. |
Card: 12 / 22 |
|
The axis of symmetry for the quadratic function |
Card: 14 / 22 |
|
If the quadratic equation x² - 6x + k = 0 has exactly one solution, what is the value of k?
|
Card: 15 / 22 |
|
For the equation to have exactly one solution, the discriminant must be zero. Thus, |
Card: 16 / 22 |
|
What is the relationship between the roots of a quadratic equation and its coefficients? |
Card: 17 / 22 |
|
For a quadratic equation ax² + bx + c = 0, the sum of the roots (r₁ + r₂) is given by -b/a, and the product of the roots (r₁r₂) is given by c/a. |
Card: 18 / 22 |
|
Find the roots of the quadratic equation 3x² - 12x + 9 = 0 using the quadratic formula.
|
Card: 19 / 22 |
|
Here, a = 3, b = -12, and c = 9. |
Card: 20 / 22 |
|
What is the effect of changing the coefficient 'a' in the quadratic equation ax² + bx + c? |
Card: 21 / 22 |
|
Changing the coefficient 'a' affects the width and direction of the parabola. If a > 0, the parabola opens upwards; if a < 0,="" it="" opens="" downwards.="" a="" larger="" |a|="" makes="" the="" parabola="" /> |
Card: 22 / 22 |





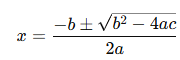
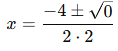 .
. 














