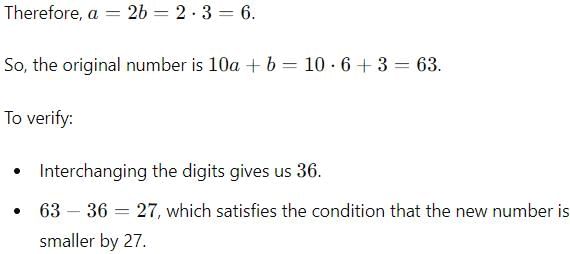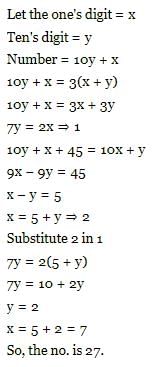Explore Exams
Login Signup
Sign in Open App
CTET & State TET Exam  >  CTET & State TET Tests  >  गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 2  >  Test: संख्या प्रणाली - 1 - CTET & State TET MCQ

Test: संख्या प्रणाली - 1 - CTET & State TET MCQ


Test Description

20 Questions MCQ Test गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 2 - Test: संख्या प्रणाली - 1

Test: संख्या प्रणाली - 1 for CTET & State TET 2025 is part of गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 2 preparation. The Test: संख्या प्रणाली - 1 questions and answers have been prepared according to the CTET & State TET exam syllabus.The Test: संख्या प्रणाली - 1 MCQs are made for CTET & State TET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: संख्या प्रणाली - 1 below.
Solutions of Test: संख्या प्रणाली - 1 questions in English are available as part of our गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 2 for CTET & State TET & Test: संख्या प्रणाली - 1 solutions in Hindi for गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 2 course. Download more important topics, notes, lectures and mock test series for CTET & State TET Exam by signing up for free. Attempt Test: संख्या प्रणाली - 1 | 20 questions in 20 minutes | Mock test for CTET & State TET preparation | Free important questions MCQ to study गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 2 for CTET & State TET Exam | Download free PDF with solutions
Test: संख्या प्रणाली - 1 - Question 1
Save

एक तीन अंकों की संख्या में, इकाई स्थान का अंक दस स्थान के अंक का दो गुना है और यह शतांक स्थान के अंक का 1.5 गुना है। यदि संख्या के सभी तीन अंकों का योग 13 है, तो यह संख्या क्या है?

Detailed Solution for Test: संख्या प्रणाली - 1 - Question 1

100a + 10b + c
c = 2b → b = c/2
c = 1.5a → a = c/1.5
c/1.5 + c/2 + c = 13
6.5c = 39
c = 6, b = 3, a = 4 ⇒ 436

Test: संख्या प्रणाली - 1 - Question 2
Save

एक दो अंकों की सकारात्मक संख्या में, इकाई स्थान पर अंक, दस के स्थान पर अंक का वर्ग के बराबर है और अंकों को बदलने पर प्राप्त संख्या और मूल संख्या के बीच का अंतर 54 है। मूल संख्या का 40% क्या है?

Detailed Solution for Test: संख्या प्रणाली - 1 - Question 2

चरण 1: अंकों को परिभाषित करें
मान लीजिए कि दस के स्थान पर अंक है x और इकाई के स्थान पर अंक है y. समस्या के अनुसार, इकाई स्थान पर अंक, दस के स्थान पर अंक के वर्ग के बराबर है। इसलिए, हम लिख सकते हैं:
y=x2

चरण 2: दो अंकों की संख्या लिखें
दो अंकों की संख्या को इस प्रकार व्यक्त किया जा सकता है:
संख्या=10x+y
चरण 1 से y को प्रतिस्थापित करते हुए, हमें मिलता है:
संख्या=10x+x2

चरण 3: अंकों को बदलने पर प्राप्त संख्या लिखें
जब हम अंकों को बदलते हैं, तो नई संख्या बनती है:
नई संख्या=10y+x
चरण 1 से y को प्रतिस्थापित करते हुए, हमें मिलता है:
नई संख्या=10x2+x

चरण 4: अंतर के लिए समीकरण स्थापित करें
समस्या के अनुसार, मूल संख्या और नई संख्या के बीच का अंतर 54 है:
(10x+x2)−(10x2+x)=54

चरण 5: समीकरण को सरल बनाएं
बाईं ओर को सरल बनाते हुए:
10x+x2−10x2−x=54
यह सरलता से:
−9x2+9x=54
पूरे समीकरण को -9 से विभाजित करने पर:
x2−x−6=0

चरण 6: द्विघात समीकरण को गुणा करें
अब हम द्विघात समीकरण को गुणा करेंगे:
(x−3)(x+2)=0
यह हमें दो संभावित समाधान देता है:
x=3 या x=−2
चूंकि x एक सकारात्मक अंक होना चाहिए, हम लेते हैं:
x=3

चरण 7: इकाई स्थान के अंक को खोजें
अब, x को प्रतिस्थापित करके y को खोजते हैं:
y=x2=32=9

चरण 8: मूल संख्या निर्धारित करें
मूल दो अंकों की संख्या है:
संख्या=10x+y=10(3)+9=30+9=39

चरण 9: मूल संख्या का 40% निकालें
मूल संख्या का 40% निकालने के लिए:
40% of 39 = 40/100 ×39 = 0.4 × 39 = 15.6

Clear all your doubts with EduRev
Test: संख्या प्रणाली - 1 - Question 3
Save

यदि एक दो अंकों की संख्या के अंकों की स्थिति बदल दी जाए, तो प्राप्त संख्या मूल संख्या से 27 कम होती है। यदि संख्या के अंकों का अनुपात 1:2 है, तो मूल संख्या क्या है?

Detailed Solution for Test: संख्या प्रणाली - 1 - Question 3

इस प्रकार, मूल संख्या 63 है।



Test: संख्या प्रणाली - 1 - Question 4
Save

एक निश्चित दो अंकों का संख्या उसके अंकों का योग तीन गुना है। यदि इसमें 45 जोड़ा जाता है, तो अंकों का क्रम उलट जाता है। वह संख्या _______ है।
Detailed Solution for Test: संख्या प्रणाली - 1 - Question 4

Test: संख्या प्रणाली - 1 - Question 5
Save

एक दो अंकों वाली संख्या के दो अंकों को बदलने पर जो संख्या प्राप्त होती है, वह मूल संख्या से 27 कम है। यदि संख्या के दो अंकों के बीच का अंतर 3 है, तो मूल संख्या क्या है?
Detailed Solution for Test: संख्या प्रणाली - 1 - Question 5

मूल संख्या – 10x + y
(10x + y) – (10y + x) = 27
9(x – y) = 27
x – y = 3
सभी दिए गए विकल्प इस शर्त का पालन नहीं करते हैं।

Test: संख्या प्रणाली - 1 - Question 6
Save

दो संख्याएँ इस प्रकार हैं कि पहली संख्या के दो गुने और दूसरी संख्या के तीन गुने का योग 100 है और पहली संख्या के तीन गुने और दूसरी संख्या के दो गुने का योग 120 है। इनमें से बड़ी संख्या कौन सी है?
Detailed Solution for Test: संख्या प्रणाली - 1 - Question 6

प्रश्न को हल करने पर हमें 72 प्राप्त होती है, जो दी गई शर्तों के अनुसार बड़ी संख्या है।




Test: संख्या प्रणाली - 1 - Question 7
Save

दो संख्याओं का अनुपात 11 : 4 है और उनका H.C.F 16 है, तो दो संख्याओं का योग ज्ञात करें।
Detailed Solution for Test: संख्या प्रणाली - 1 - Question 7

दी गई जानकारी:

दो संख्याओं का अनुपात 11 : 4 है।

H.C.F 16 है।

उपयोग की गई अवधारणा:

(1) दो संख्याओं के लिए अनुपात y : z।

पहली संख्या का मान = H.C.F × y

दूसरी संख्या का मान = H.C.F × z

गणना:

पहली संख्या का मान = 16 × 11 = 176

दूसरी संख्या का मान = 16 × 4 = 64

आवश्यक योग = 176 + 64 = 240

∴ आवश्यक उत्तर 240 है।

Test: संख्या प्रणाली - 1 - Question 8
Save

एक संख्या को 2, 3, 4, 5 या 6 से विभाजित करने पर हर बार शेषफल 1 होता है। लेकिन यह संख्या 7 से पूरी तरह विभाज्य है। यह संख्या 250 और 350 के बीच है, इस संख्या के अंकों का योग होगा
Detailed Solution for Test: संख्या प्रणाली - 1 - Question 8

इस समस्या को हल करने के लिए, हमें एक ऐसा संख्या खोजना होगा जो निम्नलिखित शर्तों को पूरा करती हो:

  1. जब इसे 2, 3, 4, 5, या 6 से विभाजित किया जाता है, तो शेषफल 1 होता है।
  2. यह संख्या 7 से विभाज्य है।
  3. यह संख्या 250 और 350 के बीच है।

आइए सबसे पहले 2, 3, 4, 5, और 6 का सामान्य गुणनखंड (LCM) खोजें, जो इन सभी संख्याओं से विभाज्य सबसे छोटी संख्या है।

LCM(2, 3, 4, 5, 6) = 60

हमें 7k के रूप की एक संख्या खोजना है, जहाँ k एक पूर्णांक है, जो 60 से विभाजित होने पर 1 का शेषफल छोड़ता है। इस अनुक्रम में संख्याओं को 60n + 1 के रूप में व्यक्त किया जा सकता है, जहाँ n एक पूर्णांक है।

अब, चलिए 250 और 350 के बीच 7 से विभाज्य 60n + 1 के पहले कुछ संख्याएँ खोजते हैं:

  • n = 4 के लिए: 60(4) + 1 = 241 (7 से विभाज्य नहीं)
  • n = 5 के लिए: 60(5) + 1 = 301 (7 से विभाज्य)

इसलिए, वह संख्या जिसे हम खोज रहे हैं, वह 301 है।

अब, चलिए इसके अंकों का योग निकालते हैं: 3 + 0 + 1 = 4

इसलिए, इस संख्या के अंकों का योग 4 है।

Test: संख्या प्रणाली - 1 - Question 9
Save

तीन लगातार विषम संख्याओं और तीन लगातार सम संख्याओं का योग 231 है। सबसे छोटी विषम संख्या और सबसे छोटी सम संख्या के बीच का अंतर 11 है। सबसे बड़ी सम संख्या और सबसे बड़ी विषम संख्या का योग क्या है?
Detailed Solution for Test: संख्या प्रणाली - 1 - Question 9

विषम संख्याएँ – x-2, x, x+2 ; सम संख्याएँ – y-2, y, y+2
3x + 3y = 231
x + y = 77
(y - 2) - (x - 2) = 11
y - x = 11
x = 33, y = 44
सबसे बड़ी सम संख्या और विषम संख्या का योग = 46 + 35 = 81

Test: संख्या प्रणाली - 1 - Question 10
Save

आठ लगातार विषम संख्याओं का योग 656 है। चार लगातार सम संख्याओं का औसत 87 है। सबसे बड़ी सम संख्या और सबसे बड़ी विषम संख्या का योग क्या है?
Detailed Solution for Test: संख्या प्रणाली - 1 - Question 10

असामान्य संख्याएँ — x-8, x-6, x-4, x-2, x, x+2, x+4, x+6
x-8 + x-6 + x-4 + x-2 + x + x+2 + x+4 + x+6 = 656
8x – 8 = 656
x = 83
समान संख्याएँ — y-2, y, y+2, y+4
4y + 4 = 87 * 4
y = 86
सबसे बड़ी समान संख्या और असामान्य संख्या का योग = 89 + 90 = 179

Test: संख्या प्रणाली - 1 - Question 11
Save

एक दो-अंकीय संख्या के अंकों का योग 6 है। यदि अंकों को उल्टा किया जाए, तो संख्या 36 से घट जाती है। संख्या ज्ञात करें?
Detailed Solution for Test: संख्या प्रणाली - 1 - Question 11

a + b = 6
(10a + b) – (10b + a) = 36, a – b = 4
हम पाते हैं कि a = 5 और b = 1
तो संख्या 51 है।

Test: संख्या प्रणाली - 1 - Question 12
Save

यदि एक तीन अंकों की संख्या के अंतिम दो अंकों के स्थानों को बदल दिया जाए, तो एक नया संख्या प्राप्त होता है जो मूल संख्या से 36 अधिक है। उस संख्या के अंतिम दो अंकों के बीच का अंतर क्या है?
Detailed Solution for Test: संख्या प्रणाली - 1 - Question 12

मान लें कि संख्या 100a + 10b + c है।
(100a + 10b + c) – (100a + 10c + b) = 36
b – c = 4

Test: संख्या प्रणाली - 1 - Question 13
Save

एक संख्या जब 143 से विभाजित होती है, तो शेषफल 31 होता है। जब वही संख्या 13 से विभाजित होती है, तो शेषफल क्या होगा?
Detailed Solution for Test: संख्या प्रणाली - 1 - Question 13

जब एक संख्या 143 से विभाजित होती है, तो शेषफल 31 होता है।

दी गई संख्या का रूप है 143x + 31 = 13(11x) + 13.2 + 5, जिससे 13(11x + 2) + 5 प्राप्त होता है।

इसलिए, जब दी गई संख्या 13 से विभाजित होती है, तो शेषफल 5 है।

Test: संख्या प्रणाली - 1 - Question 14
Save

एक उचित संख्या का अंक 4 से घटकर हर का अंक है। यदि अंक को 15 से बढ़ाया जाए और हर को 4 से घटाया जाए, तो हमें 6 मिलता है। उचित संख्या ज्ञात कीजिए?
Detailed Solution for Test: संख्या प्रणाली - 1 - Question 14

मान लेते हैं कि भिन्न (p-4)/p है।
अब, (p -4 + 15)/(p-4) = 6
हमें p = 7 मिलता है।
इसलिए भिन्न = 3/7 है।

Test: संख्या प्रणाली - 1 - Question 15
Save

जब एक संख्या को दूसरे संख्या के 20 प्रतिशत में जोड़ा जाता है, तो हमें दूसरे संख्या का 150 प्रतिशत मिलता है। पहले और दूसरे संख्या के बीच अनुपात ज्ञात करें।
Detailed Solution for Test: संख्या प्रणाली - 1 - Question 15

a + (20/100)*b = (150/100)*b
a:b = 13:10

Test: संख्या प्रणाली - 1 - Question 16
Save

यदि दो संख्याएँ समान भाजक द्वारा विभाजित की जाती हैं, तो शेषफल क्रमशः 3 और 4 होते हैं। यदि इन दोनों संख्याओं का योग समान भाजक द्वारा विभाजित किया जाता है, तो शेषफल 2 होता है। भाजक क्या है?
Detailed Solution for Test: संख्या प्रणाली - 1 - Question 16

चरण-दर-चरण समाधान:

चरण 1: संख्याओं का निरूपण
मान लें कि भाजक है d, और दो संख्याएँ हैं a और b.

  • जब a को d द्वारा विभाजित किया जाता है, तो शेषफल = 3।
  • जब b को d द्वारा विभाजित किया जाता है, तो शेषफल = 4।

चरण 2: संख्याओं का योग
a और b का योग देता है:
a + b = (d का एक गुणांक) + 7
जब योग को d द्वारा विभाजित किया जाता है, तो शेषफल 2 होता है।
7 ≡ 2 (mod d)

चरण 3: भाजक के लिए हल करें
समीकरण को सरल बनाएं:
7 - 2 = 5
इसका मतलब है कि d को 5 को सही ढंग से विभाजित करना चाहिए।
d का केवल एक संभावित मान है 5.

भाजक है 5.

Test: संख्या प्रणाली - 1 - Question 17
Save

एक संख्या 24 घटाने पर उसकी दो-तिहाई हो जाती है। उस संख्या का एक-आठवां भाग क्या है?
Detailed Solution for Test: संख्या प्रणाली - 1 - Question 17

मान लीजिए संख्या को a कहते हैं।
a - 24 = 2a/3
इसे हल करने पर हमें a = 72 मिलता है।
इसलिए उस संख्या का एक-आठवां भाग = 72/8 = 9

Test: संख्या प्रणाली - 1 - Question 18
Save

तीन संख्याएँ 4:3:5 के अनुपात में हैं। यदि तीसरी संख्या को तीन गुना करने और पहली एवं दूसरी संख्या के योग के बीच का अंतर 64 है, तो पहली और तीसरी संख्या के बीच का अंतर क्या है?
Detailed Solution for Test: संख्या प्रणाली - 1 - Question 18

15x – (7x) = 64, हमें x = 8 मिलता है।
पहली और तीसरी संख्या के बीच का अंतर = 5x – 4x = x = 8

Test: संख्या प्रणाली - 1 - Question 19
Save

एक संख्या का एक-पांचवा भाग जब उस संख्या के एक-तिहाई भाग से घटाया जाता है, तो 24 प्राप्त होता है। उस संख्या का वर्ग ज्ञात करें।
Detailed Solution for Test: संख्या प्रणाली - 1 - Question 19

a/3 – a/5 = 24
a = 180, तो वर्ग = 32400

Test: संख्या प्रणाली - 1 - Question 20
Save

किसी संख्या का 25% दूसरी संख्या के 65% का 2 गुना है। दूसरी संख्या और पहली संख्या का अनुपात क्या है?
Detailed Solution for Test: संख्या प्रणाली - 1 - Question 20

(25/100)*a = 2*(65/100)*b
b:a = 5:26

50 videos|152 docs|70 tests
Join Course
Information about Test: संख्या प्रणाली - 1 Page
In this test you can find the Exam questions for Test: संख्या प्रणाली - 1 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: संख्या प्रणाली - 1, EduRev gives you an ample number of Online tests for practice
Download as PDF

Important Questions for संख्या प्रणाली - 1

Find all the important questions for संख्या प्रणाली - 1 at EduRev.Get fully prepared for संख्या प्रणाली - 1 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the संख्या प्रणाली - 1 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of संख्या प्रणाली - 1 resources.

संख्या प्रणाली - 1 MCQs with Answers

Prepare for the संख्या प्रणाली - 1 within the CTET & State TET exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for संख्या प्रणाली - 1 गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 2

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace संख्या प्रणाली - 1 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up
within 7 days!
Takes less than 10 seconds to signup