ओलंपियाड परीक्षा: प्राथमिक आकृतियों की समझ - CTET & State TET MCQ
20 Questions MCQ Test गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 2 - ओलंपियाड परीक्षा: प्राथमिक आकृतियों की समझ
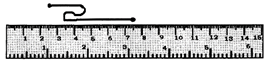
यदि चित्र में दिखाया गया धागा सीधा खींचा जाए, तो इसकी लंबाई का सबसे निकटतम अनुमान कौन सा होगा?
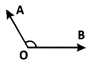
0∘ से अधिक और 90∘ से कम मापने वाले कोण को क्या कहा जाता है?
एक कोण जो 0∘ मापता है उसे ___ कोण कहा जाता है।
जिस कोण की माप 180∘ है, उसे क्या कहा जाता है?
5:20 पर घड़ी की दो सुइयों के बीच कौन सा प्रकार का कोण बनता है?
l और m दो रेखाएँ हैं जो एक-दूसरे के प्रति लंबवत हैं। उनके बीच के कोण का माप क्या है?
179∘ इनमें से किस प्रकार के कोण का उदाहरण है?
जब किसी कोण की भुजा को बढ़ाया जाता है, तो इसका माप कैसे बदलता है?
निम्नलिखित में से कौन सा कोण एक प्रतिकूल कोण का माप है?
कोण ∠PRQ में निम्नलिखित में से कौन से दो भुजाएँ हैं?
हम 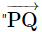 का प्रतीकात्मक रूप से कैसे लिखते हैं कि यह
का प्रतीकात्मक रूप से कैसे लिखते हैं कि यह 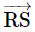 ' के लंबवत है?
' के लंबवत है?
वे रेखाएँ जो एक ही तल पर होती हैं और किसी भी बिंदु पर एक-दूसरे को नहीं काटती हैं, उन्हें क्या कहा जाता है?
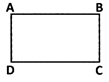
दी गई आकृति में कितने समानांतर रेखाओं के जोड़े हैं?
|
50 videos|152 docs|70 tests
|
|
50 videos|152 docs|70 tests
|