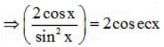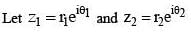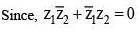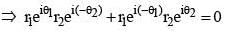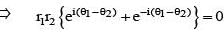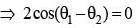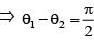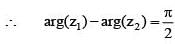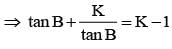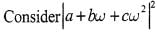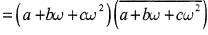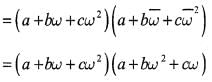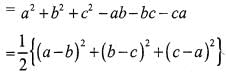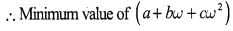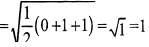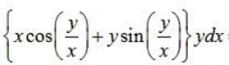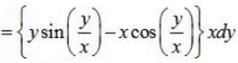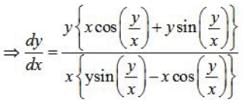AWES TGT Maths Mock Test - 1 - AWES TGT/PGT MCQ
30 Questions MCQ Test AWES TGT Mock Test Series 2025 - AWES TGT Maths Mock Test - 1
Who is depicted on the first UK banknotes with his portrait?
In the QS World University Rankings 2024, what is IIT Bombay's global ranking in engineering?
At the primary level, National Education Policy 2020 proposes__________ as the medium of instruction across the nation.
Let f(x) be a polynomial for which the remainders when divided by x – 1, x – 2, x – 3 respectively 3, 7, 13. Then the remainder of f(x) when divided by (x – 1) (x – 2) (x – 3) is
If acos x + bsin x = c, then the value of (asin x – bcos x)² is:
For any two non-zero complex numbers z1 and z2 if then the difference of amplitudes of z1 and z2 is
If the sum of n terms of an A.P. is 2n2 + 5n, then find the 4th term.
If f : R → R be a differentiable function, such that f (x + 2y) = f (x) + f (2y) + 4xy for all x, y ∈ R then
In a triangle ABC if A = π/4 and tanB tanC = K, then K must satisfy.
Let A (1,1,1) , B (2, 3, 5) and C (-1, 0, 2) be three points, then equation of a plane parallel to the plane ABC which is at a distance 2 from origin is
If a,b,c are integers not all equal andw is a cube root of unity (ω ≠ 1) then the minimum value of |a + bω+ cω2| is
solution of {x cos (y/x) + ysin(y/x)} ydx = {ysin(y/x) - x cos (y/x)} xdy is
The area bounded by the curve y = 2x - x2 and the line x + y = 0 is
If α (≠ 1) is a fifth root of unity and b (≠ 1) is a fourth root of unity, then z = (1 + α) (1 + β) (1 + α2) (1 + β2) (1 + α3) (1 + β3) equals
A lady wants to select one cotton saree and one polyster saree from a textile shop. If there are 15 cotton and 13 polyster varieties in that shop, in how many ways can she pick up two sarees?
If the tangent at the point (h, k) on the hyperbola meets the auxiallary circle of the hyperbola in two points whose ordinates y1, y2 then
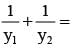
Nidhi has 6 friends. In how many ways can she invite one or more of them to a party at her home?
If n is a +ve integer, then the binomial coefficients equidistant from the beginning and the end in the expansion of (x+a)n are
On a railway track, there are 20 stations. The number of tickets required in order that it may be possible to book a passenger from every station to every other is
The first term of an A.P. of consecutive integer is p2 + 1. The sum of (2p + 1) terms of this series can be expressed as
What is the approximate value of 1 radian in degree measure?
In a simultaneous throw of two coins the probability of getting at least one head is