VITEEE PCME Mock Test - 7 - JEE MCQ
30 Questions MCQ Test VITEEE: Subject Wise and Full Length MOCK Tests - VITEEE PCME Mock Test - 7
Height of two towers are 20 m and 80 m. Join foot of the one tower to the top of other and vice versa. Find the height of intersection point from the horizontal plane.
Let X have the Poisson distribution with parameter λ, such that P(X = k + 1) = r(k) P(X = k). The value r(k) is
In a binomial distribution, the mean is 4 and variance is 3. Then, its mode is
If the ratio of the roots of the equation x² + bx + c = 0 is the same as that of x² + qx + r = 0, then:
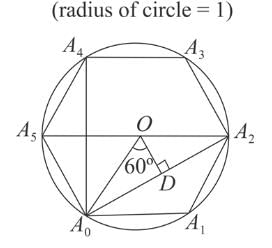
Let A₀, A₁, A₂, A₃, A₄, and A₅ be the consecutive vertices of a regular hexagon inscribed in a unit circle. The product of the lengths of A₀A₁, A₀A₂, and A₀A₄ is:
Let g(x) be a polynomial of degree one & f(x) be defined by 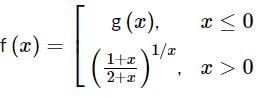 such that f(x) is continuous f′(1) = f(−1), then g(x) is
such that f(x) is continuous f′(1) = f(−1), then g(x) is
The lines whose vector equations are 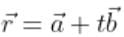 and
and 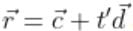 are coplanar, if
are coplanar, if
An alternating voltage is applied across a circuit. As a result,
flows in it. The power consumed per cycle is
Masses of two isobars 29Cu64 and 30Zn64 are 63.9298 u and 63.9292 u respectively. It can be concluded from these data that :
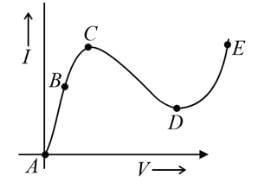
From the graph between current (I) and voltage (V) shown, identify the portion corresponding to negative resistance:
Which among the following electromagnetic wave has the longest wavelength?
A convex lens has a mean focal length of 20 cm. The dispersive power of the material of the lens is 0.02. The longitudinal chromatic aberration for an object at infinity is:
Image formed by a convex lens is virtual and erect when the object is placed
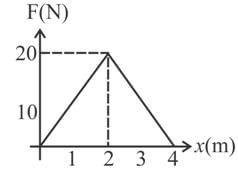
The graph between the resistive force F acting on a body and the distance covered by the body is shown in the figure. The mass of the body is 25 kg and initial velocity is 2 m s−1. When the distance covered by the body is 4 m, its kinetic energy would be,
Given: pK1 = 2.0, pK2 = 9.9 and pK3 = 3.9
From the information, calculate the isoelectric pH (pI) of aspartic acid.
Which of the following is not correct for an ideal gas as per first law of thermodynamics?
Directions: The following question has four choices out of which ONLY ONE is correct.
In Haber process, 30 L of dihydrogen and 30 L of dinitrogen were taken for reaction which yielded only 50% of the expected product. What would be the composition of gaseous mixture under the aforesaid condition in the end?
The two functional groups present in a typical carbohydrate are:
Directions: Fill in the blank with the most appropriate preposition from the given options.
To know the reality, you have to dig _____ her past.
Choose the correct option to replace the word(s) given in brackets:
(Smoke) is injurious to health.
Direction: In the question given below, a part of the sentence is underlined. Below are given alternatives to the underlined part which may improve the sentence. Choose the correct alternative. In case no improvement is needed your answer is 'No improvement'.
My opinion for the film is that it will bag the national award.
Study the table and answer the question.
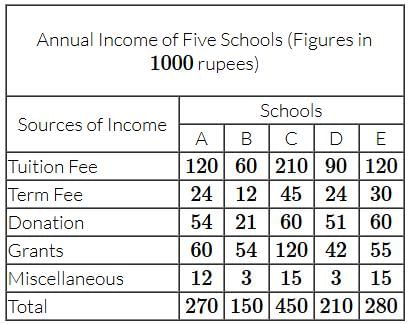
Which school has the lowest ratio of income by way of grants and tuition fees?
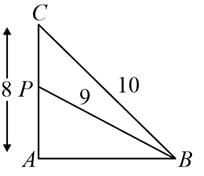
ABC is a triangle in which ∠A = 90°. Let P be any point on side AC. If BC = 10 cm, AC = 8 cm, and BP = 9 cm, then AP is equal to:
|
1 videos|7 docs|63 tests
|
|
1 videos|7 docs|63 tests
|




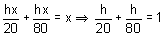



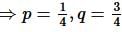
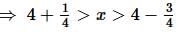
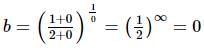

 is a/an
is a/an = arg(z + i) - arg(z - i) = tan-1
= arg(z + i) - arg(z - i) = tan-1 - tan-1
- tan-1 =
=  tan-1
tan-1 =
=  , i.e. x2 + y2 - 2x
, i.e. x2 + y2 - 2x = 1 is the equation of a circle.
= 1 is the equation of a circle. 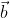 and
and  ,
,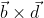 , which is perpendicular to the line joining the points on the plane with position vectors
, which is perpendicular to the line joining the points on the plane with position vectors 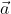 and
and 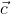
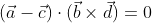 , which is the required condition for the given lines to be coplanar.
, which is the required condition for the given lines to be coplanar. 



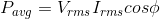

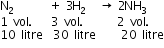
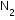 used = 5 L, left = 30 - 5 = 25 L
used = 5 L, left = 30 - 5 = 25 L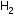 used = 15 L, left = 30 - 15 = 15 L
used = 15 L, left = 30 - 15 = 15 L