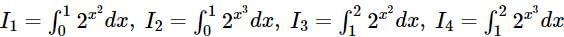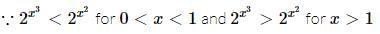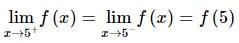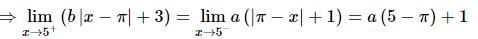VITEEE PCME Mock Test - 3 - JEE MCQ
30 Questions MCQ Test VITEEE: Subject Wise and Full Length MOCK Tests - VITEEE PCME Mock Test - 3
The unit vector which is orthogonal to the vector 5i + 2j + 6k and is coplanar with the vectors 2i + j + k and i – j + k is
What is the orthogonal trajectory of the family of parabolas y2 = 4ax (a is arbitrary)?
The p.d.f. of a random variable X is:
f(x) = 3(1 - 2x2), 0 < x < 1 = 0, otherwise
Then P = ______
= ______
Line y = c is a tangent to the parabola y2 = 4ax if c is equal to
The order and the degree of the differential equation whose general solution is given by: y = (a1 + a2) sin(x + a3) - a4ex + a5, where a1, a2, a3, a4 and a5 are arbitrary constants, respectively are
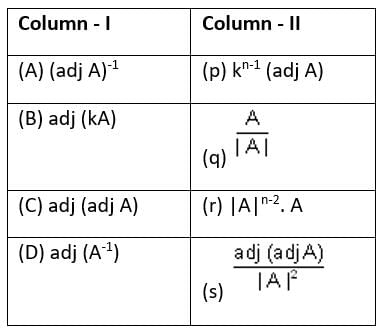
The correct match of Column - I to Column - II, if A is a non-singular matrix of order n × n, is
Let f(x) = 15 - |x -10| and g(x) = f(f(x)) then g(x) is non differentiable at.
A curve passes through the point (0, 1) and its gradient at (x, y) on it is y(xy - 1). The equation of the curve is
The length of the latus rectum of an ellipse is one-third of the major axis. Its eccentricity would be
The combined equation of the asymptotes of the hyperbola 2x2 + 5xy + 2y2 + 4x + 5y = 0 is
The relation R in the set {1, 2, 3} is given by R∈{(1, 2), (2, 1)}. What can we conclude about R?
If x² + 6x − 27 > 0 and −x² + 3x + 4 > 0, then x lies in the interval:
A man is walking on a straight line. The arithmetic mean of the reciprocals of the intercepts of this line on the coordinate axes is 1/4. Three stones A, B, and C are placed at the points (1,1), (2,2), and (4,4) respectively. Then which of these stones is/are on the path of the man?
In L.P.P., the constraints 5x + 4y ≥ 20, x ≤ 6, y ≤ 4 form
If the projection of 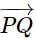 on the axes OX, OY, OZ are respectively 12, 3, and 4, then the magnitude of
on the axes OX, OY, OZ are respectively 12, 3, and 4, then the magnitude of 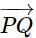 is:
is:
If α, β are the roots of the equation ax² + bx + c = 0, then the roots of the equation a(x + 2)² + b(x + 2) + c = 0 are:
The equation of an ellipse whose eccentricity is 1/2 and the vertices are (4,0) and (10,0) is:
Let R be a relation on a set A such that R = R⁻¹, then R is:
The eccentricity of the hyperbola whose asymptotes are 3x + 4y = 2 and 4x - 3y + 5 = 0 is:
If sin²θ + sin²ϕ = 1/2 and cos²θ + cos²ϕ = 3/2, then cos²(θ − ϕ) = ?
If the function 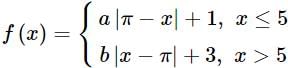 is continuous at x = 5,, then the value of a − b is:
is continuous at x = 5,, then the value of a − b is:
For any three complex numbers z₁, z₂, and z₃, the given expression: z₁Im(z̅₂z₃) + z₂Im(z̅₃z₁) + z₃Im(z̅₁z₂) is equal to:
|
1 videos|7 docs|63 tests
|
|
1 videos|7 docs|63 tests
|


 , then
, then  - 4 is divisible by
- 4 is divisible by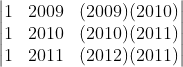
 R3 - R2; R2
R3 - R2; R2  R2 - R1
R2 - R1
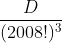 - 4 = (2009)2 (2010) (2) - 4
- 4 = (2009)2 (2010) (2) - 4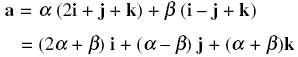
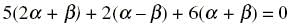
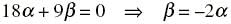
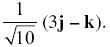







 = 0
= 0




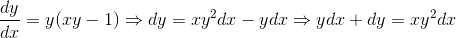
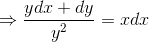

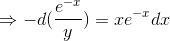
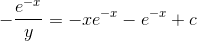
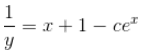
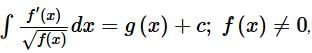 then g(x) =
then g(x) =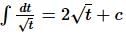
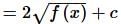
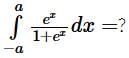
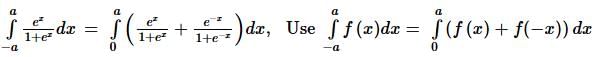
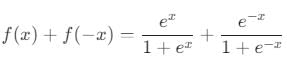
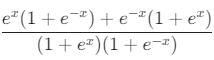
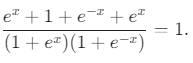
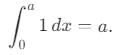
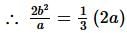
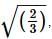 eccentricity is always positive of an ellipse.
eccentricity is always positive of an ellipse. 
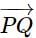 on the axes are given, we can represent
on the axes are given, we can represent 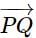 as:
as: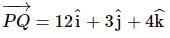
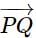 is given by:
is given by:
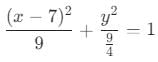
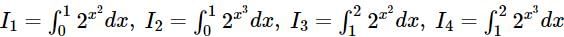 then
then