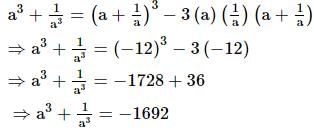VITEEE PCME Mock Test - 6 - JEE MCQ
30 Questions MCQ Test VITEEE: Subject Wise and Full Length MOCK Tests - VITEEE PCME Mock Test - 6
Let  and
and  be three non-coplanar vectors such that
be three non-coplanar vectors such that  =
=  and
and .
.
If , then
, then
 and
and  be three non-coplanar vectors such that
be three non-coplanar vectors such that  =
=  and
and .
.If
 , then
, thenA player tosses 2 fair coins. He wins Rs. 5 if 2 heads appear, Rs. 2 If 1 head appears and Rs. 1 if no head appears, then variance of his winning amount is
Area of region satisfying x ≤ 2, y ≤ |x|, x ≥ 0 and y ≥ 0 is-
If x = a(cost + tsint) and y = a(sint − tcost), 0 < t < π/2. The value of d2y/dx2 would be:
Three letters, to each of which corresponds an envelope, are placed in the envelopes at random. The probability that all the letters are not placed in the right envelopes, is
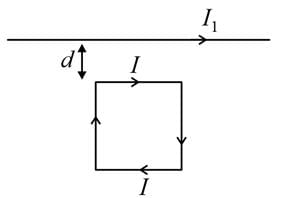
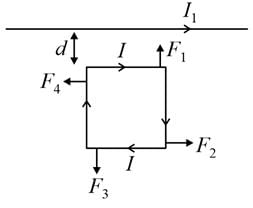
Two parallel infinite wires separated by distance 'd' carry currents are shown in figure.
The distance from a third infinite wire be kept parallel to wire carrying current I1, the wire such that it stays in equilibrium is

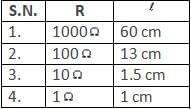
Which of the above is inconsistent for the given meter bridge?
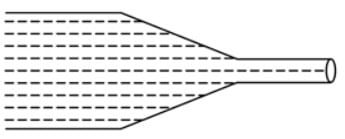
Water flows through a frictionless duct with a cross-section varying as shown in the figure. The pressure P at points along the axis is represented by,
A square loop, carrying a steady current I is placed in horizontal plane near a long straight conductor carrying a steady current I1 at a distance of d from the conductor as shown in figure. The loop will experience
According to Stokes' law, the relation between terminal velocity (vt) and viscosity of the medium (η) is:
A daniel cell is balanced at 125 cm length of a potentiometer wire. When the cell is circuited by a resistance of 2 Ω, the balance length is obtained at 100 cm. The internal resistance of the Daniel cell is
Assertion: Electric field due to a charged long conducting sheet does not depend on position of point from sheet.
Reason: Charged conducting sheet have uniform linear charge density.
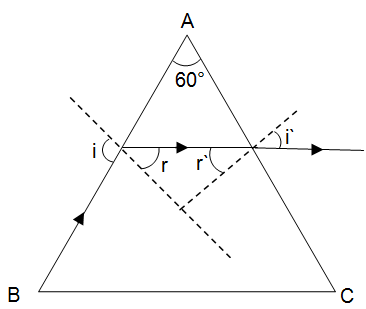
At what angle will a ray of light incident on one face of an equilateral prism, so that the emergent ray may graze the second surface of the prism (μ = 1.5)? (sin 42° = 0.67, sin 18° = 0.31, sin 28° = 0.465)
A battery is of emf E and internal resistance r. The value of external resistance R, so that the power across external resistance is maximum, is
Using the data given below, find out the strongest reducing agent.
Eo (CrO4-2/Cr3+) = 1.33 V, Eo (CI2/CI-) = 1.36 V
Eo (Mn) = 1.51 V, Eo (Cr3+/Cr) = –0.74 V
A chemical reaction will be spontaneous if it is accompanied by a decrease of
By the action of concentrated HCl on potassium chlorate, we get this mixture of gases.
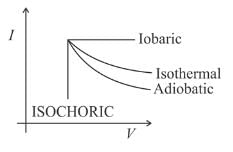
If W₁, W₂, W₃, and W₄ are the work done in isothermal, adiabatic, isobaric, and isochoric reversible processes, the correct order for expansion will be:
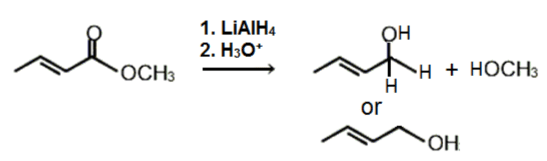
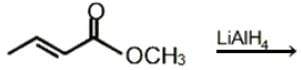
Which of the following is the major product of the given reaction?
In this question, a part of the sentence is bold/underlined. Below are given alternatives to the bold/underlined part at A, B and C which may improve the sentence. Choose the correct alternative to edit and improve the sentence. In case no improvement is needed, your answer is D.
Too many people rush into the world of credit and don't stop to think about how their actions could affect their credit score and ability to qualify for credit in the future.
In a certain code language, 'Ka Bi Pu' stands for 'you are intelligent', 'Ya Lo Ka Wo' stands for 'they seem very intelligent', 'Lo Pu Le' stands for 'you can see'. Which of the following code words stands for 'are' in this language?
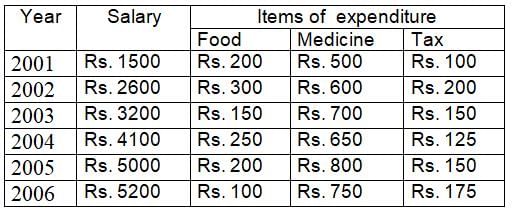
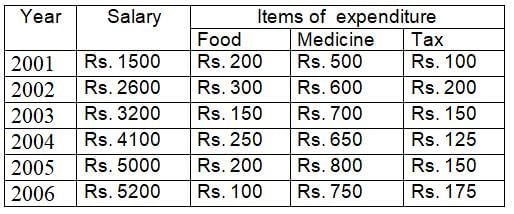
The ratio of total salary and expenditure during the period 2001 to 2006 is:
The following pie chart shows the expenditure (in percentage) of five companies P, Q, R, S and T in the year 2016.
Total Expenditure =Rs. 48 crores

By how much percent expenditure of company Q and R together is greater than that of company P?
The given question is followed by two statements I and II. Answer each question using the following instructions.
Mark option (a) if the question can be answered by using one of the statements alone, but cannot be answered using the other statement alone.
Mark option (b) if the question can be answered by using either statement alone.
Mark option (c) if the question can be answered by using both statements together, but cannot be answered using either statement alone.
Mark option (d) if the question cannot be answered even by using both statements together.
Does line L pass through the origin of the co-ordinate plane?
I. Line L is perpendicular to the Y-axis.
II. Line L passes through the point (6, 0).
The question is based on the pie chart given below:
Total Sunrays received in 1 min = 3600 units
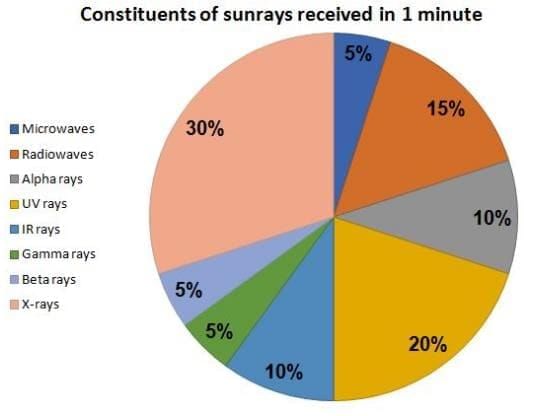
If the human body can withstands a maximum of 9720 unit of IR rays, when exposed to the sun continuously, then what is the maximum time (in min) that any person could stand in the sum without crossing the threshold limit of IR rays?
The sum of a number and its reciprocal is −12. What would be the sum of cubes of the two (the number and its reciprocal)?
|
1 videos|7 docs|63 tests
|
|
1 videos|7 docs|63 tests
|






 , for |sin y| = 1 and sin x = 1
, for |sin y| = 1 and sin x = 1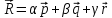 ⇒
⇒ 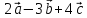 =
= 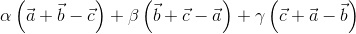
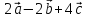 =
= 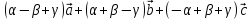
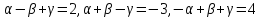 [Since
[Since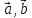 and
and 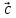 are non-coplanar]
are non-coplanar]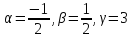

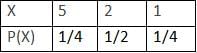


 Variance of X = ∑X2 P(X) - (∑XP(X))2
Variance of X = ∑X2 P(X) - (∑XP(X))2

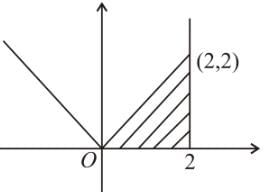
 sq. units
sq. units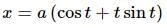
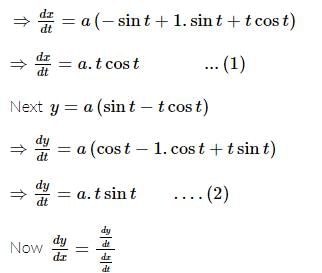
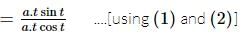
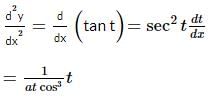
 is
is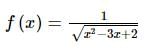










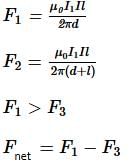
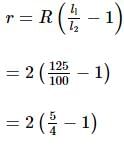
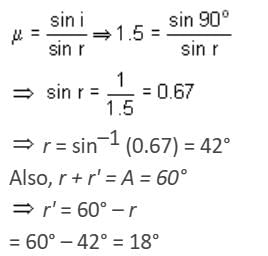
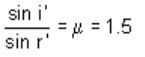
 0.31 = 0.465
0.31 = 0.465