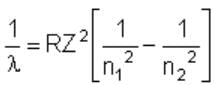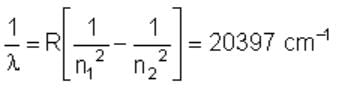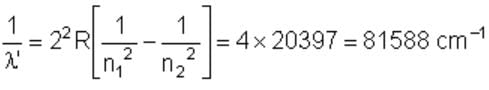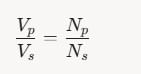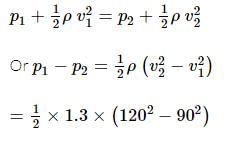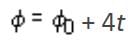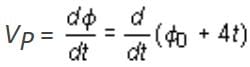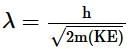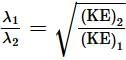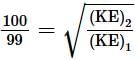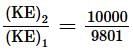VITEEE PCME Mock Test - 1 - JEE MCQ
30 Questions MCQ Test VITEEE: Subject Wise and Full Length MOCK Tests - VITEEE PCME Mock Test - 1
A circle on the focal radii of a parabola, described as diameter touches the
The equation of a circle touching the coordinate axes and the line x cos α + y sin α = 2 is x2 + y2 – 2gx + 2gy + g2 = 0, where g is equal to
What is the equation of the line which passes through (4, −5) and is perpendicular to 3x + 4y + 5 = 0?
The coefficient of x⁵ in the expansion of (1 + x)²¹ + (1 + x)²² + … + (1 + x)³⁰ is:
If A is a square matrix of order n×n such that A² = A, and I is the unit matrix of order n×n, then the expression (I + A)ⁿ is equal to:
If (2n + r)r, where n ∈ N and r ∈ N, is expressed as the sum of k consecutive odd natural numbers, then k is equal to:
If the reading of the ideal voltmeter shown in the circuit is 2V, the internal resistance of the two identical cells is
A sample containing same number of two nuclei A and B start decaying. The decay constant of A and B are 10λ and λ. The time after which NA/NB becomes 1/e is
The wave number of the energy emitted when electrons come from fourth orbit to second orbit in hydrogen is 20,397 cm–1. The wave number of energy for the same transition in He+ is
Three bodies A,B and C have equal area which are painted red, yellow and black respectively. If they are at the same temperature, then
By Huygens wave theory of light, we cannot explain the phenomenon of
Air is streaming past a horizontal airplane wing such that its speed is 120 m/s over the upper surface and 90 m/s at the lower surface. If the density of air is 1.3 kg/m³, what will be the gross lift on the wing? If the wing is 10 m long and has an average width of 2 m.
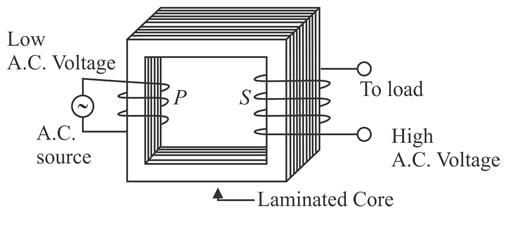
The primary and secondary coils of a transformer have 50 and 1500 turns, respectively. If the magnetic flux φ linked with the primary coil is given by φ = φ0 + 4t, where φ is in weber, t is time in second and φ0 is a constant, then the output voltage across the secondary coil is
An electron is continuously accelerated in a vacuum tube by applying potential difference. If its de Broglie wavelength is decreased by 1%, the change in the kinetic energy of the electron is nearly
The incorrect statement(s) among (a) - (c) is (are) :
(a) W(VI) is more stable than Cr(VI).
(b) in the presence of HCl, permanganate titrations provide satisfactory results.
(c) some lanthanoid oxides can be used as phosphors.
All of the following are mentioned as places in which memories are stored, except
Direction :In the sentence given below a part is bold/underlined and for that part options are given. Choose the most suitable option that can replace the bold part.
Sabotage came from the French saboter, which means "to clatter with wooden shoes (sabots)."
|
1 videos|7 docs|63 tests
|
|
1 videos|7 docs|63 tests
|


 is continuous at x = 0 then (p, q) is
is continuous at x = 0 then (p, q) is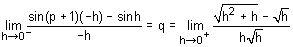


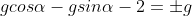
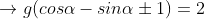

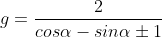
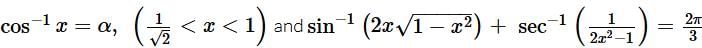 , then tan−1(2x) equals
, then tan−1(2x) equals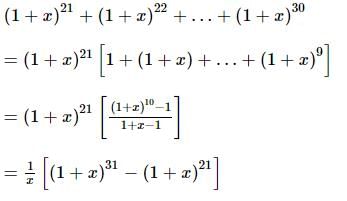
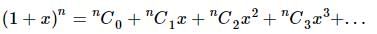
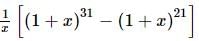 is given by
is given by 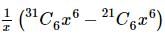 .
. 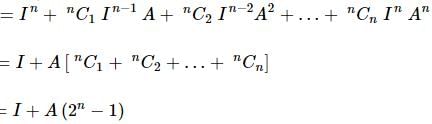
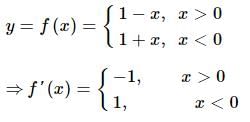
 then value of k is
then value of k is
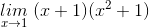 =
= 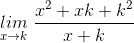




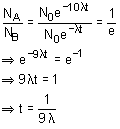
 t
t t = E0 sin
t = E0 sin 
 =
=  + 2E0 . E0 cos
+ 2E0 . E0 cos
 = E0
= E0  = constant
= constant