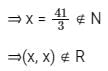Test: Equivalence Relations - Engineering Mathematics MCQ
10 Questions MCQ Test Engineering Mathematics - Test: Equivalence Relations
Relation R is defined as
R = {(a, b) | (a - b) = km for some fixed integer m and a, b, k ∈ z}, then R is
What is the nature of relation R, if R is defined as R = {(x, y) : 2x + y = 41, x, y ∈ N}?
A relation R is said to be circular if aRb and bRc together imply cRa. Which of the following options is/are correct?
Let m ∈ Z and consider the relation Rm defined by a Rm b if and only if a ≡ b mod m. Then Rm is -
Consider R and S be two equivalence relations, which of the following is true regarding the R and S
Let, R = {(a, b): a,b ∈ Z and (a + b) is even}, then R is
Which of the following is an equivalence relation on the set of all functions from Z to Z ?
Let, R = {(a, b): a, b ϵ N and a2 = b}, then what is the relation R
Suppose A is a finite set with n elements. The number of elements and the rank of the largest equivalence relation on A are
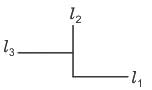
Let L denote the set of all straight lines in a plane. Let a relation R be l R m if l is perpendicular to m ∀ l, m ∈ L. Then R is:
|
65 videos|133 docs|94 tests
|