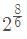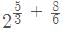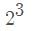Test: घातांक - 1 - CTET & State TET MCQ
15 Questions MCQ Test गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 2 - Test: घातांक - 1
यदि n 2 से अधिक एक सकारात्मक पूर्णांक है, तो 3n + 3n + 3n – 3n-2 का सबसे बड़ा अभाज्य गुणांक क्या है?
यदि 'x' और 'y' गैर-नकारात्मक पूर्णांक हैं, तो x + y का मान क्या होगा?
(1) x4 सम है, जहाँ x एक प्रमुख संख्या है।
(2) xy विषम है।
उस n का मान खोजें जो समीकरण 2(-3)4n = 18(27)n+2 को संतुष्ट करता है।
एक परमाणु घटना से निकलने वाले विकिरण की तीव्रता को एक घातीय पैमाने पर मापा जाता है, जहां दूसरा और चौथा बिंदु क्रमशः 25 और 625 की तीव्रता को दर्शाते हैं। उस पैमाने पर, तीसरे बिंदु पर तीव्रता कितनी होगी?
सकारात्मक पूर्णांक P 1 और 30 के बीच है। P का मान क्या है?
(1) P के पास कम से कम दो अभाज्य गुणक हैं
(2) P का घन 300 से कम है
एक रेडियोधर्मी तत्व की आधी-आयु को उस समय की मात्रा के रूप में परिभाषित किया जाता है जो तत्व की मात्रा को आधा करने के लिए आवश्यक होती है। यदि एक तत्व की आधी-आयु 3 वर्ष है, तो तत्व को अपनी मूल मात्रा के एक-आठवें हिस्से तक पहुंचने में कितना समय लगेगा?
क्या xy≥ 1 है यदि दोनों x और y गैर-शून्य पूर्णांक हैं?
(1) y = -x
(2) y = 2k जहाँ k एक गैर-शून्य पूर्णांक है
1 से 30 के बीच स्थित सकारात्मक पूर्णांक P का मान ज्ञात करें जो एक पूर्ण वर्ग है।
(1) P का कम से कम एक प्राइम फैक्टर है।
(2) P का घन 300 से कम है।
यदि k एक पूर्णांक है, तो का मान खोजें।
(1) 2r – 2k = 26, जहाँ r एक पूर्णांक है।
(2) 14 + k = 3k – 2r, जहाँ r एक पूर्णांक है।
|
50 videos|152 docs|70 tests
|
|
50 videos|152 docs|70 tests
|



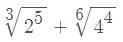
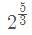 +
+ 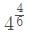
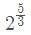 +
+ 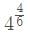
 +
+