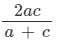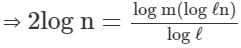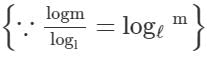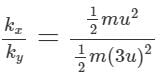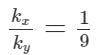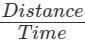MPTET Varg 2 Math Mock Test - 3 - MPTET MCQ
30 Questions MCQ Test MPTET Varg 2 (MPESB Middle School) Mock Test Series 2026 - MPTET Varg 2 Math Mock Test - 3
What is the logarithm of 1/9 in a system whose base is 3?
In covering a certain distance, the speeds of A and B are in the ratio of 3 ∶ 4. A takes 20 minutes more than B to reach the destination. The time taken by A to reach the destination is
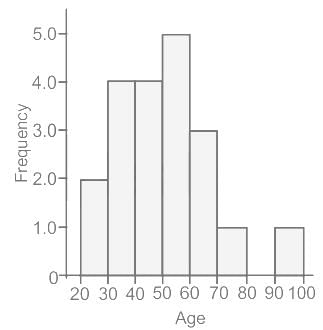
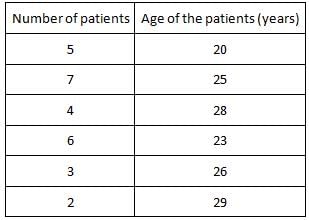
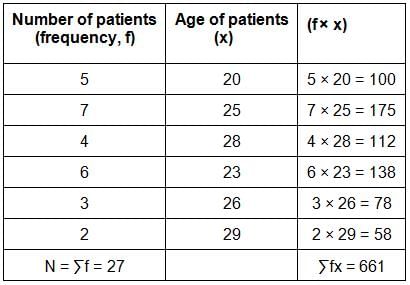
The given data is of the age of the patients in a hospital. What is the mean age of all the patients taken together?
If the radius of the hemisphere is 7a, then its total surface area (in cm2) is
If the ratio of the areas of two squares is 9 : 1, then the ratio of their perimeters is
Calculate the cylinder’s total surface area if its radius is 7 cm and height is 12 cm.
A person invests Rs. 10,000 for two years in such a scheme that it will provide 10% p.a. for the first year and 20% p.a. for the second year. Find the compound interest earned.
Which cognitive skill of bloom’s taxonomy could be evaluated in this below question?
Question: Name all the patterns drawn on the blackboard.
If logℓ x, logm x and logn x are in A.P., then value of n2 is (where x ≠ 1)
The levels of Van Hiele's geometric reasoning are given below. They are arranged in random order.
(i) Relationships among figures
(ii) Recognition of figures
(iii) Axiomatic Reasoning
(iv) Deductive Reasoning & formal proofs
(v) Analysis of components of figures
Choose the correct sequence.
The parking rates of car in a railway station parking are depicted as follows:
(a) Up to 2 hrs – Rs. 50
(b) More than 2 hrs and up to 5 hrs – Rs. 75
(c) After 5 hrs – Rs. 10 per extra hour up to 8 hrs.
(d) More than 8 hrs and up to 12 hrs – Rs. 150
(e) More than 12 hrs and up to 24 hrs – Rs. 250
Rajeev parks his car at 7.00 a.m. and comes back to pick it up at 4.30 p.m. on the same day. How much money does he have to pay?When the class intervals have equal width, the height of a rectangle in a histogram represents
Two objects, x, and y have equal mass and are moving with speeds u and 3u respectively. Their kinetic energies kx and ky are related as
Which of the following statements explain the application of 'FORCE'
A. Force may bring a change in the shape of an object
B. Force may make an object move
C. Force cannot change the direction of motion of an object
D. Force can change the speed of an object
E. Force can be push or pull
Choose the correct answer from the options given below:
An iron ball at 40°C is dropped in mug containing water at 40°C. The heat will
Approximately how much distance per minute the Earth is rotating?
|
1 docs|15 tests
|
|
1 docs|15 tests
|


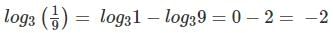
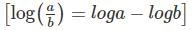

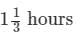
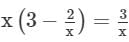 then the value of
then the value of 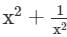 is
is
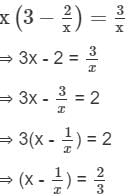
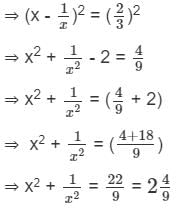
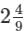 .
.
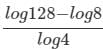 is:
is: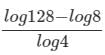
 is 2.
is 2.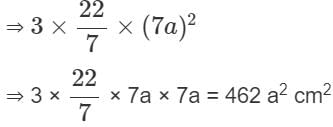
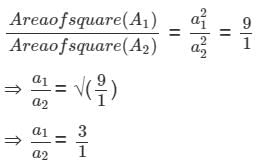
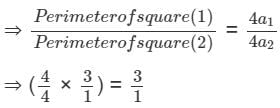
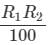
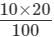 = 32%
= 32%