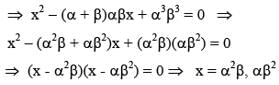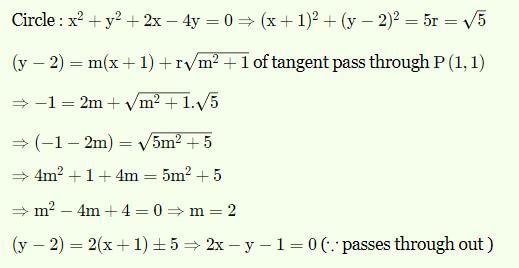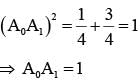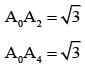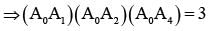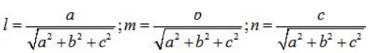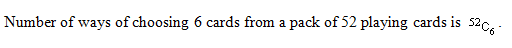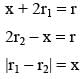HPSC PGT Mathematics Mock Test - 5 - HPSC TGT/PGT MCQ
30 Questions MCQ Test HPSC PGT Mock Test Series 2025 - HPSC PGT Mathematics Mock Test - 5
Where Pratap Singh revolted against the British?
In 1757, who was defeated in the Battle of Plassey?
Arrange the words given below in the order in which they appear in an English dictionary.
1. Sugary
2. Subtle
3. Sudoku
4. Sucres
5. Sullen
Select the figure that will come next in place of ?.

Each diagonal element of a skew-symmetric matrix is
Number of ordered pairs (a,b) of real numbers such that (a + ib)2012 = a - ib holds good is
If α,β are roots of ax2 + bx + c = 0, then roots of a3x2 + abcx + c3 = 0 are
If F1 & F2 are the feet of the perpendiculars from the foci S1 & S2 of an ellipse +
= 1 on the tangent at any point P on the ellipse, then (S1F1) . (S2F2) is equal to
The tangent from the point of intersection of the lines 2x – 3y + 1 = 0 and 3x – 2y –1 = 0 to the circle x2 + y2 + 2x – 4y = 0 is
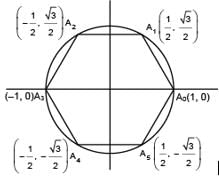
Let A0 A1A2A3 A4A5 be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths of the line segments A0A1, A0 A2 and A0 A4 is
lx + my + n = 0 is a tangent line to the circle x2 + y2 = r2, if
If l, m, n are the direction cosines and a, b, c are the direction ratios of a line then
What is the number of ways of choosing 6 cards from a pack of 52 playing cards?
The coefficient of a4b3c2d in the expansion of (a – b + c – d)10 is
The y-intercept of the circle x2 + y2 + 4x + 8y - 5 = 0 is
Radii of the smallest and the largest circle passing through a point lying on the sides of a rectangle with vertices (± 2, ± 1) and touching the circle x2 + y2 = 9, are r1 and r2 respectively. Let d = |r1 – r2| then minimum value of d is
The eccentricity of the hyperbola 4x2–9y2–8x = 32 is
A plane π passes through the point (1, 1, 1). If b, c, a are the direction ratios of a normal to the plane, where a, b, c (a < b < c) are the prime factors of 2001, then the equation of the plane π is
The sum of the series 2 + 6 + 18 + ….+ 4374 is:
Write A = {1, 4, 9, 16, 25} in set builder form.
A tangent to the parabola x2 = 4ay meets the hyperbola x2 - y2 = a2 at two points P and Q, then midpoint of P and Q lies on the curve
The area bounded by the curves y= |x−1| and y = 1 is given by