CSIR NET Mathematical Science Mock Test - 7 - UGC NET MCQ
30 Questions MCQ Test CSIR NET Exam Mock Test Series 2025 - CSIR NET Mathematical Science Mock Test - 7
In an examination 80% candidates passed in English and 85% candidates passed in Mathematics. If 73% candidates passed in both these subjects, then what per cent of candidates failed in both the subjects?
A dishonest milkman professes to sell his milk at cost price but he mixes it with water and thereby gains 25%. The percentage of water in the mixture is:
Direction: In this question a series given with one number missing. Choose the correct alternative from the given ones that will complete the series.
X50Z, T42V, P34R, L26N,____.
In a class of 52 students the number of boys is two less than the number of girls. Average weight of the boys is 42 kg. while the average weight of all the 52 students is 40 kg Approximately what is the average weight of the girls?
Average age of seven persons in a group is 30 years, the average age of five persons of this group is 31 years. What is the average age of the other two persons in the group?
If an article is sold for a gain of 7% instead of selling it at a loss of 13%, a trader gets Rs.1080 more. What is the selling price of the article, when the article is sold at a profit of 25%?
A shopkeeper expects a gain of 20 % on his cost price. If in a week his sale is of Rs. 540, then what is his profit?
Let w be the wronskian of two linearly independent solutions of ODE 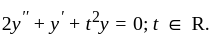 Then for all t, there exist a constant
Then for all t, there exist a constant  such that w(t)
such that w(t)
If A is Skew-Hermitian matrix, then iA is—
If A is a square matrix, and A2 = A, then A is—
Let In be an Identity matrix of order n, then—
If A is a singular matrix, then its characteristic root are—
If A and B are Symmetric matrices, then AB are Symmetric iff—
If W1 and W2 are subspaces of vector space v and W1 is the subspace spanned by vectors α1, ....., αn If α1 ,........αn ,∈ W2 then
Let 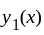 and
and  be two linearly independent solutions of the differential equation
be two linearly independent solutions of the differential equation 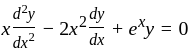 satisfying
satisfying 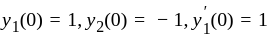 and
and 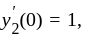 Then the
Then the
wronskian of 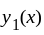 and
and 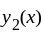 at
at 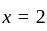 i. e.
i. e. 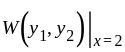 is equal to
is equal to
Let 〈Fn〉 is a sequence of measurable functions (on the some domain).
If f is bounded and measurable on closed interval [a, b]
(A) 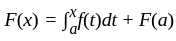
(B) 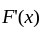 exist for almost all
exist for almost all 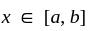
(C) 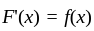 almost everywhere in [a, b]
almost everywhere in [a, b]
(D)  almost everywhere in [a, b]
almost everywhere in [a, b]
Given collection C of open intervals of the form 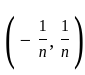
If 〈 fn 〉 is a sequence of mappings of a countable set D into a metric space Y such that for each x ∈ D the closure of the set {fn(x) : 0 ≤ n < ∞} is compact.
Consider the quadratic forms q and p given by—








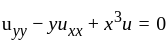 is-
is-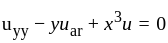
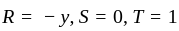
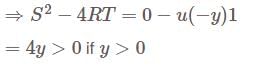
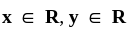
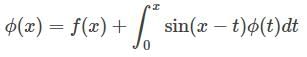
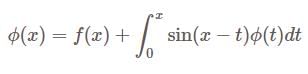
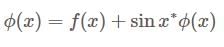
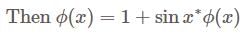
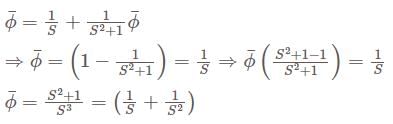
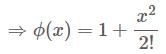
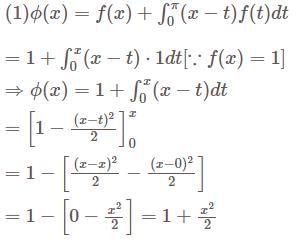


 A is Skew-Hermitian
A is Skew-Hermitian 

 is Hermitian.
is Hermitian.

 is—
is—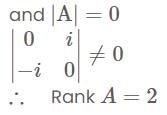
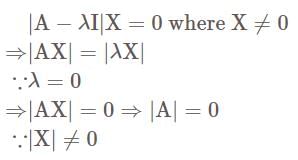
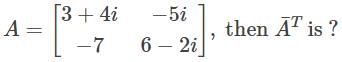
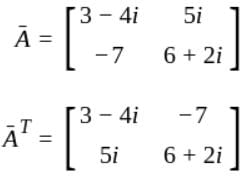

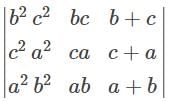 is—
is—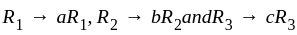 ,
,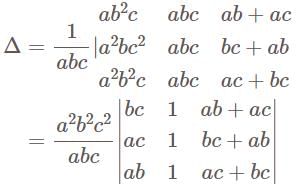

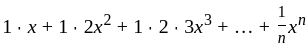
 is
is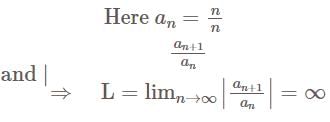
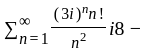
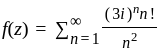
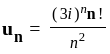
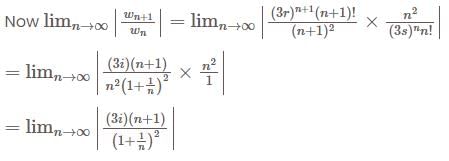


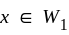
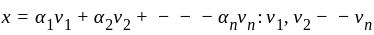 are scalar
are scalar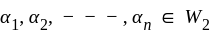
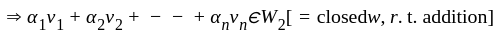
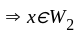

 such that
such that  for all
for all  Then
Then
 is invertible function with self-inverse, hence
is invertible function with self-inverse, hence  is both one
is both one  one and onto
one and onto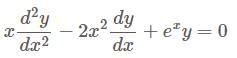
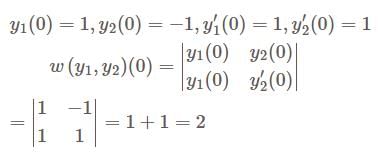
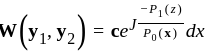 where
where 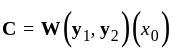 where
where  Interval
Interval
 we have
we have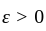 and
and 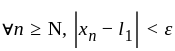 and
and 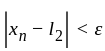
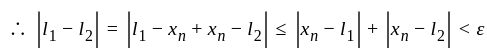
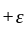
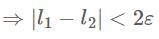
 which contradicts the statement that
which contradicts the statement that 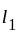 and
and 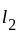 are distinct. Thus, the sequence
are distinct. Thus, the sequence 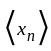 have atmost one limit.
have atmost one limit.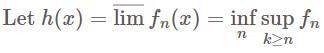
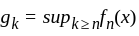 is a measurable function and in then inf gk is a measurable function too and so
is a measurable function and in then inf gk is a measurable function too and so 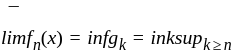 is also measurable.
is also measurable.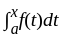 is of bounded variation, then so
is of bounded variation, then so 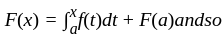
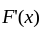 exist for almost all x in [a, b]
exist for almost all x in [a, b]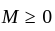 such that
such that 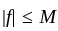 , set
, set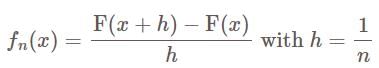
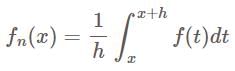
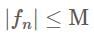
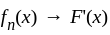 almost everywhere
almost everywhere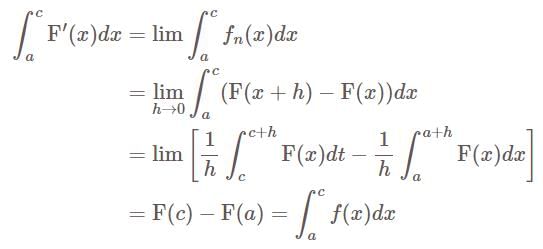
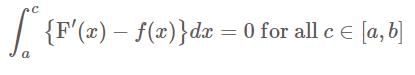
 almost everywhere in [a, b]
almost everywhere in [a, b] almost everywhere in [a, b]
almost everywhere in [a, b]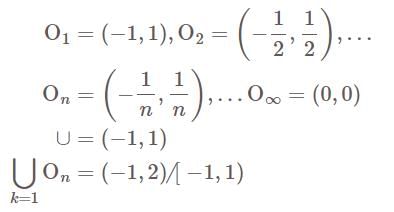
 By the sequential compactness of the closure of
By the sequential compactness of the closure of  we can pick a subsequence
we can pick a subsequence  of
of  such that
such that  converges. Choose a subsequence
converges. Choose a subsequence  of
of  such that
such that  converges. Continuing this, we obtain a subsequence
converges. Continuing this, we obtain a subsequence  convergent on
convergent on  . Consider the 'diagonal' sequence
. Consider the 'diagonal' sequence 
 a subsequence of
a subsequence of  and
and  converges.
converges.











