CSIR NET Mathematical Science Mock Test - 3 - UGC NET MCQ
30 Questions MCQ Test CSIR NET Exam Mock Test Series 2025 - CSIR NET Mathematical Science Mock Test - 3
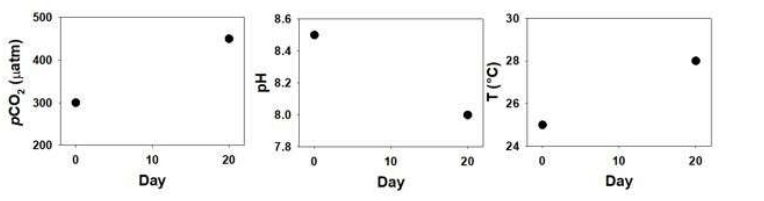
Given figure represents pH, partial pressure of CO2 (pCO2), and temperature (T) in an experiment conducted in a water sample over 20 days. Which of the following statements can definitely be made based on this experiment?

Consider the following four statements.
Statement 1: “Statement 3 is true.”
Statement 2: “Statement 1 is true”
Statement 3: “Statement 1 is true and Statement 2 is false”
Statement 4: “Statements 1, 2 and 3 are false”
Which of the above statements must be true for the four statements to be mutually consistent?
Statement 2: “Statement 1 is true”
Statement 3: “Statement 1 is true and Statement 2 is false”
Statement 4: “Statements 1, 2 and 3 are false”
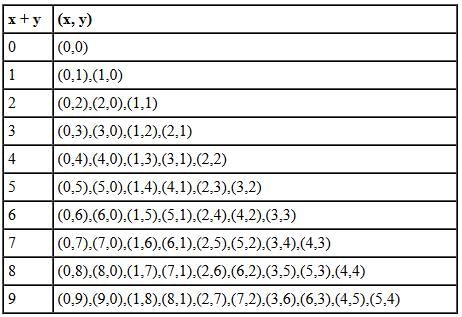
The number of three digit PINs, in which the third digit is the sum of the first two digits, is
Rajesh went to Sunil’s house situated 1 km North-East of his house. From there, he went to Arjun’s house that is situated 707 m South of Sunil’s house. What is the distance between Rajesh’s current location and his house (to the nearest metre)?
By selling two items at the same price, a person gains 20% on one item and loses 20% on the other. Then over all
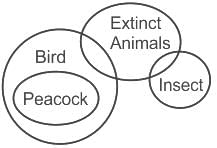
An appropriate diagram to depict the relationships between the categories INSECTS, BIRDS, EXTINCT ANIMALS and PEACOCKS is
In a group of 7 people, 4 have exactly one sibling and 3 have exactly two siblings. Two people selected at random from the group, what is the probability that they are NOT siblings?
Person A tells the truth 30% of the times and B tells the truth 40% of the times, independently. What is the minimum probability that they would contradict each other?
The initial value problem 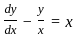 , x > 0; y(0) = 1 has
, x > 0; y(0) = 1 has
Let X1,X2,...,Xn be a random sample from a normal distribution with mean μ and standard deviation σ. Which of the following is NOT a sufficient statistic for μ?
Let X0, X1 ......Xp (p ≥ 2) be independent and identically distributed random variables with mean 0 and variance 1. Suppose Yi = X0 + Xi, i = 1....p. The first principal component based on the covariance matrix of Y = (Y1...., Yp)T is
For each n ≥ 1 define fn : ℝ → ℝ by  x ∈ ℝ where √ denotes the non-negative square root. Wherever
x ∈ ℝ where √ denotes the non-negative square root. Wherever  exists, denote it by f(x). Which of the following statements is true?
exists, denote it by f(x). Which of the following statements is true?
Let B(0,1) = {(x,y) ∈ ℝ2|x2 + y2 < 1} be the open unit disc in ℝ2, ∂B(0, 1) denote the boundary of B(0,1), and v denote unit outward normal to ∂B(0, 1). Let f : ℝ2 → ℝ be a given continuous function. The Euler-Lagrange equation of the minimization problem 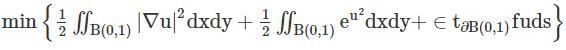 subject to
subject to 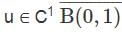 is
is
Let (an)n≥1 be a bounded sequence in ℝ. Which of the following statements is FALSE?
Let A : ℝm → ℝn be a non-zero linear transformation. Which of the following statements is true?
Suppose X = (X1, X2, X3, X4)T has a multivariate normal N4(0, I2 ⊗ Σ), where I2 is the 2 × 2 identity matrix, ⊗ is the Kronecker product, and Σ =  . Define Z =
. Define Z = 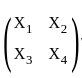 and Q = ((Qij)) = ZTZ. Suppose
and Q = ((Qij)) = ZTZ. Suppose  denotes a chi-square random variate with n degrees of freedom, and Wm(n, Σ) denotes a Wishart distribution of order m with parameters n and Σ. The distribution of (Q11 + Q12 + Q21 + Q22) is
denotes a chi-square random variate with n degrees of freedom, and Wm(n, Σ) denotes a Wishart distribution of order m with parameters n and Σ. The distribution of (Q11 + Q12 + Q21 + Q22) is
The number of solutions of the equation x2 = 1 in the ring ℤ/105ℤ is
Let p(x) be a real polynomial of degree 3 then 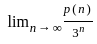 is
is
Let Z and W be independent Poisson random variables with parameters 4 and 5, respectively. Which of the following statements are correct?
Let a continuous random variable A follow Uniform (-2, 2). Define B = A2. Which of the following statements are NOT true for A and B?
Let A ∈ M2(ℝ).
Which of the following statements is/are true?
Let [x] denote the integer part of x for any real number x. Which of the following sets have non-zero Lebesgue measure?
Let 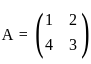 and ϕ : ℝ2 → ℝ2 → ℝ be the bilinear map defined by
and ϕ : ℝ2 → ℝ2 → ℝ be the bilinear map defined by
ϕ(v, w) = vT Aw. Choose the correct statement from below:
Which of the following is/are Units in ℤ(√3)?
Consider the linear programming problem: max {x1 + x2 + x3} subject to constraints
x1 + x2 - x3 ≤ 1
x1 + x3 ≤ 2
0 ≤ x1 ≤ 1/2, x2 ≥ 0
and 0 ≤ x3 ≤ 1
Which of the following statements are true?
For z ∈ ℂ \ {0}, let 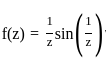 and g(z) = f(z)sin (z). Which of the following statements are true?
and g(z) = f(z)sin (z). Which of the following statements are true?
In a standard linear regression model, let R2 and R̅2, respectively, denote the coefficient of determination and adjusted coefficient of determination. Which of the following statements are true?



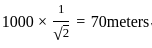 .
.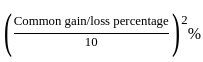
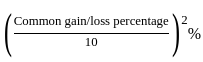
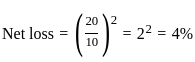
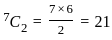
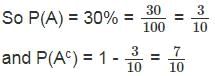
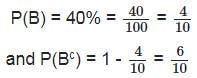
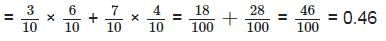
 which is linear in y
which is linear in y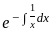 = e-logx = 1/x
= e-logx = 1/x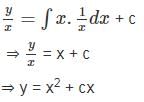
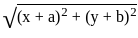
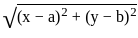
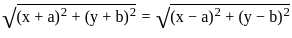
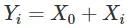 and since the Xi's are i.i.d., their variances and covariances can be computed easily.
and since the Xi's are i.i.d., their variances and covariances can be computed easily.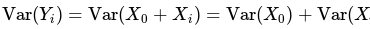
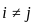 ) is
) is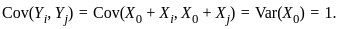
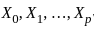 are independent and identically distributed (i.i.d.) random variables with mean 0 and variance 1.
are independent and identically distributed (i.i.d.) random variables with mean 0 and variance 1.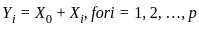 .
.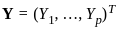 .
.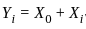 where, X0
where, X0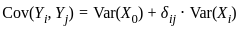 , where
, where 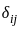 is the Kronecker delta.
is the Kronecker delta.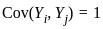 when
when 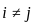 (because of the common X0).
(because of the common X0).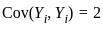 when
when 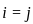 .
.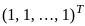 .
.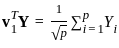
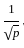 to ensure unit length of the eigenvector.
to ensure unit length of the eigenvector.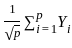
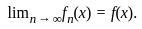
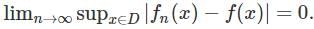
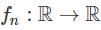 defined by
defined by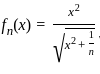
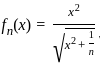
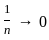 . So, for large n , the function fn(x) approaches
. So, for large n , the function fn(x) approaches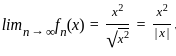
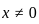
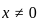 we have,
we have, 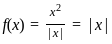
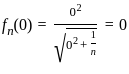
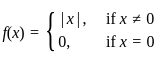
 ,
,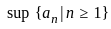 is the smallest number that is greater than or equal to all the terms of the sequence.
is the smallest number that is greater than or equal to all the terms of the sequence.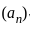 ,
, 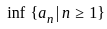 is the largest number that is less than or equal to all the terms of the sequence.
is the largest number that is less than or equal to all the terms of the sequence.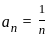 .
.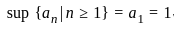
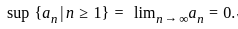
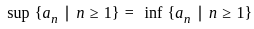 , this means that the least upper bound and the greatest lower bound are the same. Let’s call this common value C.
, this means that the least upper bound and the greatest lower bound are the same. Let’s call this common value C.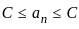 , which implies that an = C for all n.
, which implies that an = C for all n.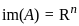 ).
).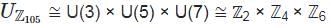
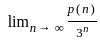
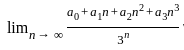 (∞/
(∞/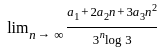 (Using L'hospital rule)
(Using L'hospital rule)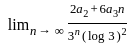
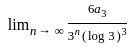
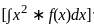 from -2 to 2, which equals 8/3, not 4/3.
from -2 to 2, which equals 8/3, not 4/3.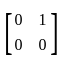
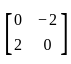
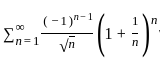 then it is
then it is is a convergent series, {bn} is a monotone sequence, and {bn} is bounded. Then
is a convergent series, {bn} is a monotone sequence, and {bn} is bounded. Then  is also convergent.
is also convergent.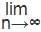 bn = 0 and, {bn} is a decreasing sequence the series ∑an is convergent.
bn = 0 and, {bn} is a decreasing sequence the series ∑an is convergent.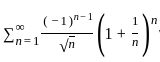
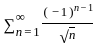 and {bn} =
and {bn} = 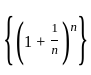
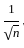 ≥ 0 for all n,
≥ 0 for all n,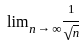 = 0 and
= 0 and 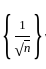 is a decreasing sequence so by Alternating series test
is a decreasing sequence so by Alternating series test 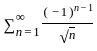
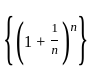 is a monotonic sequence and bounded as
is a monotonic sequence and bounded as 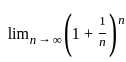 = e
= e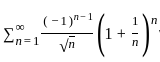 is convergent
is convergent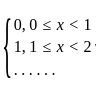
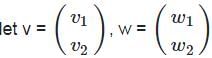
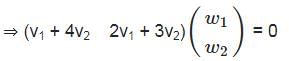
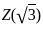
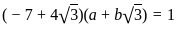
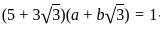
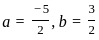
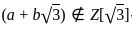
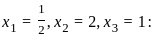
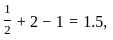 which violates
which violates 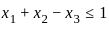 .
.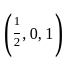 satisfies all the constraints:
satisfies all the constraints: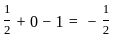 , which satisfies ≤ 1.
, which satisfies ≤ 1.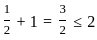
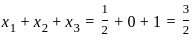 , which is less than the optimal value of 3.
, which is less than the optimal value of 3.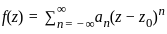 where an for n < 0 are not all zero.
where an for n < 0 are not all zero.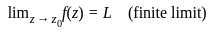 where L is a complex number. If we define f(z0) = L, then f(z) becomes analytic at z0.
where L is a complex number. If we define f(z0) = L, then f(z) becomes analytic at z0.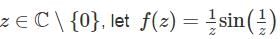 and g(z) = f(z)sin (z) .
and g(z) = f(z)sin (z) .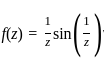 :
: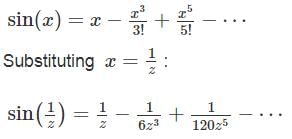
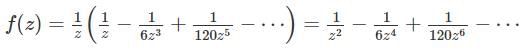
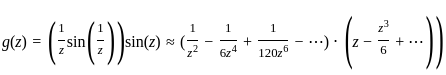
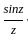 is nearly equal to when z → 0
is nearly equal to when z → 0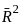 refers to the adjusted coefficient of determination in a standard linear regression model.
refers to the adjusted coefficient of determination in a standard linear regression model.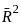 is typically less than or equal to R2 .
is typically less than or equal to R2 .










