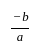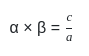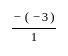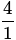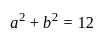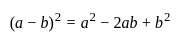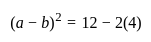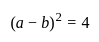CTET & State TET Exam > CTET & State TET Tests > गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 2 > गणित पेपर 2 (बीजगणित - II) - CTET & State TET MCQ
गणित पेपर 2 (बीजगणित - II) - CTET & State TET MCQ
Test Description
10 Questions MCQ Test गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 2 - गणित पेपर 2 (बीजगणित - II)
गणित पेपर 2 (बीजगणित - II) for CTET & State TET 2025 is part of गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 2 preparation. The गणित पेपर 2 (बीजगणित - II) questions and answers have been
prepared according to the CTET & State TET exam syllabus.The गणित पेपर 2 (बीजगणित - II) MCQs are made for CTET & State TET 2025 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for गणित पेपर 2 (बीजगणित - II) below.
Solutions of गणित पेपर 2 (बीजगणित - II) questions in English are available as part of our गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 2 for CTET & State TET & गणित पेपर 2 (बीजगणित - II) solutions in
Hindi for गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 2 course. Download more important topics, notes, lectures and mock
test series for CTET & State TET Exam by signing up for free. Attempt गणित पेपर 2 (बीजगणित - II) | 10 questions in 10 minutes | Mock test for CTET & State TET preparation | Free important questions MCQ to study गणित और शिक्षाशास्त्र (Mathematics) CTET & TET Paper 2 for CTET & State TET Exam | Download free PDF with solutions
Detailed Solution for गणित पेपर 2 (बीजगणित - II) - Question 1
Detailed Solution for गणित पेपर 2 (बीजगणित - II) - Question 2
गणित पेपर 2 (बीजगणित - II) - Question 3
निम्नलिखित अभिव्यक्ति को सरल बनाएं।
(4x + 1)2 − (4x + 3) (4x − 1)
Detailed Solution for गणित पेपर 2 (बीजगणित - II) - Question 3
गणित पेपर 2 (बीजगणित - II) - Question 4
समिकरण x2 - 3x + 4 = 0 के मूलों का योग और गुणनफल क्या है?
Detailed Solution for गणित पेपर 2 (बीजगणित - II) - Question 4
Detailed Solution for गणित पेपर 2 (बीजगणित - II) - Question 5
Detailed Solution for गणित पेपर 2 (बीजगणित - II) - Question 6
Detailed Solution for गणित पेपर 2 (बीजगणित - II) - Question 7
गणित पेपर 2 (बीजगणित - II) - Question 8
यदि -2 द्विघात समीकरणों ay2 + ay + 3 = 0 और y2 + y + b = 0 का एक सामान्य मूल है, तो a2b है:
Detailed Solution for गणित पेपर 2 (बीजगणित - II) - Question 8
गणित पेपर 2 (बीजगणित - II) - Question 9
यदि दो वास्तविक संख्याओं के वर्गों का योग 12 है और संख्याओं का गुणनफल 4 है, तो संख्याओं के बीच का अंतर ज्ञात करें।
Detailed Solution for गणित पेपर 2 (बीजगणित - II) - Question 9
गणित पेपर 2 (बीजगणित - II) - Question 10
यदि α और β x2 - 7x + 1 = 0 समीकरण के मूल हैं, तो α4 + β4 का मान क्या होगा?
Detailed Solution for गणित पेपर 2 (बीजगणित - II) - Question 10
|
50 videos|152 docs|70 tests
|
Information about गणित पेपर 2 (बीजगणित - II) Page
In this test you can find the Exam questions for गणित पेपर 2 (बीजगणित - II) solved & explained in the simplest way possible.
Besides giving Questions and answers for गणित पेपर 2 (बीजगणित - II), EduRev gives you an ample number of Online tests for practice
|
50 videos|152 docs|70 tests
|
Download as PDF


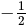
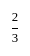


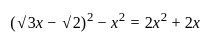
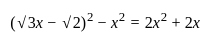 एक द्विघात समीकरण नहीं है।
एक द्विघात समीकरण नहीं है।