All Exams >
Civil Engineering (CE) >
Engineering Mechanics >
All Questions
All questions of Impulse, Momentum & Collision for Civil Engineering (CE) Exam
The kinetic energy of a body is stated to increase by 300 percent. The corresponding increase in the momentum of the body will be ____%- a)50
- b)100
- c)200
- d)300
Correct answer is option 'B'. Can you explain this answer?
The kinetic energy of a body is stated to increase by 300 percent. The corresponding increase in the momentum of the body will be ____%
a)
50
b)
100
c)
200
d)
300
|
|
Neha Joshi answered |
- Kinetic energy (K.E): The energy possessed by a body by the virtue of its motion is called kinetic energy.
The expression for kinetic energy is given by:
KE = (1/2)mv2
Where m = mass of the body and v = velocity of the body
KE = (1/2)mv2
Where m = mass of the body and v = velocity of the body
- Momentum (p): The product of mass and velocity is called momentum.
Momentum (p) = mass (m) × velocity (v)
The relationship between the kinetic energy and Linear momentum is given by:
As we know,
KE = (1/2)mv2
Divide numerator and denominator by m, we get
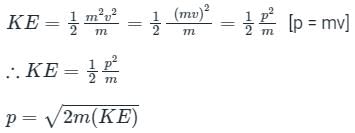
Calculation:
Let initial Kinetic energy = KE1 = E
Given that:
Final kinetic energy (K.E2) = K.E1 + 300 % of KE1 = E + 3E = 4E
The relation between the momentum and the kinetic energy is given by:
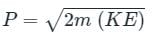
Final momentum (P') will be:
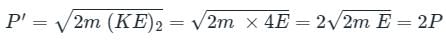
Increase in momentum (ΔP) = P' - P = 2P - P = P
% Increase =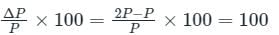
The relationship between the kinetic energy and Linear momentum is given by:
As we know,
KE = (1/2)mv2
Divide numerator and denominator by m, we get
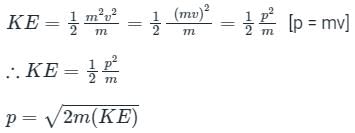
Calculation:
Let initial Kinetic energy = KE1 = E
Given that:
Final kinetic energy (K.E2) = K.E1 + 300 % of KE1 = E + 3E = 4E
The relation between the momentum and the kinetic energy is given by:
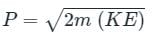
Final momentum (P') will be:
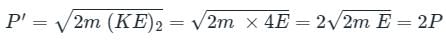
Increase in momentum (ΔP) = P' - P = 2P - P = P
% Increase =
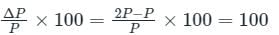
Collision of Elastic Bodies in case of indirect impact of a body with a fixed plane is- a)v cos θ = eu sin α
- b)u cos θ = ev cos α
- c)v cos θ = eu cos α
- d)v sin θ = eu sin α
Correct answer is option 'C'. Can you explain this answer?
Collision of Elastic Bodies in case of indirect impact of a body with a fixed plane is
a)
v cos θ = eu sin α
b)
u cos θ = ev cos α
c)
v cos θ = eu cos α
d)
v sin θ = eu sin α
|
|
Neha Joshi answered |
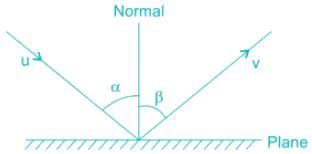
Consider a body having an indirect impact on a fixed plane as shown in the figure.
where, u = Initial velocity of the body, v = Final velocity of the body, α = Angle, which the initial velocity of the body makes with the line of impact, β = Angle which the final velocity of the body makes with the line of impact, and e = Coefficient of restitution.
The component of u, along the line of impact, will cause the direct ‘impact’ of the body with the fixed plane.
The other component of u along the perpendicular to the line of impact will not affect the phenomenon of impact and will be equal to the other component of v (i.e., along the perpendicular to the line of impact).
We know that velocity of approach = u cos α and velocity of separation = v cos β
And the coefficient of restitution is,
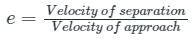
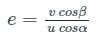
v cos β = eu cos α
Two inelastic spheres of masses 10 kg each move with velocities of 15 m/s and 5 m/s respectively in the same direction. The loss in kinetic energy when they collide- a)500 Nm
- b)0 Nm
- c)250 Nm
- d)1000 Nm
Correct answer is option 'C'. Can you explain this answer?
Two inelastic spheres of masses 10 kg each move with velocities of 15 m/s and 5 m/s respectively in the same direction. The loss in kinetic energy when they collide
a)
500 Nm
b)
0 Nm
c)
250 Nm
d)
1000 Nm
|
|
Sahil Majumdar answered |
Explanation:
Given Data:
- Mass of each sphere, m = 10 kg
- Initial velocities, u1 = 15 m/s and u2 = 5 m/s
Loss in Kinetic Energy:
- The initial total kinetic energy of the system is given by:
KE_initial = (1/2) * m1 * u1^2 + (1/2) * m2 * u2^2
= (1/2) * 10 * 15^2 + (1/2) * 10 * 5^2
= 1125 + 125
= 1250 J
- After the collision, the final total kinetic energy of the system is given by:
KE_final = (1/2) * (m1 + m2) * V^2
where V is the common final velocity of both spheres.
- Since the collision is inelastic, kinetic energy is not conserved. The loss in kinetic energy is given by:
Loss in KE = KE_initial - KE_final
- From the law of conservation of momentum:
m1 * u1 + m2 * u2 = (m1 + m2) * V
10 * 15 + 10 * 5 = 20 * V
150 + 50 = 20V
V = 10 m/s
- Substituting the value of V in the equation for KE_final:
KE_final = (1/2) * 20 * 10^2
= 1000 J
- Therefore, the loss in kinetic energy is:
Loss in KE = 1250 - 1000
= 250 J
Therefore, the correct answer is option C, 250 Nm.
Given Data:
- Mass of each sphere, m = 10 kg
- Initial velocities, u1 = 15 m/s and u2 = 5 m/s
Loss in Kinetic Energy:
- The initial total kinetic energy of the system is given by:
KE_initial = (1/2) * m1 * u1^2 + (1/2) * m2 * u2^2
= (1/2) * 10 * 15^2 + (1/2) * 10 * 5^2
= 1125 + 125
= 1250 J
- After the collision, the final total kinetic energy of the system is given by:
KE_final = (1/2) * (m1 + m2) * V^2
where V is the common final velocity of both spheres.
- Since the collision is inelastic, kinetic energy is not conserved. The loss in kinetic energy is given by:
Loss in KE = KE_initial - KE_final
- From the law of conservation of momentum:
m1 * u1 + m2 * u2 = (m1 + m2) * V
10 * 15 + 10 * 5 = 20 * V
150 + 50 = 20V
V = 10 m/s
- Substituting the value of V in the equation for KE_final:
KE_final = (1/2) * 20 * 10^2
= 1000 J
- Therefore, the loss in kinetic energy is:
Loss in KE = 1250 - 1000
= 250 J
Therefore, the correct answer is option C, 250 Nm.
Identify correct statement(s) about the coefficient of restitution 'e' -- a)If e =1, The collision is perfectly elastic
- b)If e = 0, The collision is perfectly elastic
- c)If e = 0,The collision is perfectly plastic
- d)If e =1, Height before impact = Height after impact
Correct answer is option 'B'. Can you explain this answer?
Identify correct statement(s) about the coefficient of restitution 'e' -
a)
If e =1, The collision is perfectly elastic
b)
If e = 0, The collision is perfectly elastic
c)
If e = 0,The collision is perfectly plastic
d)
If e =1, Height before impact = Height after impact
|
|
Neha Joshi answered |
Coefficient of restitution (e): The coefficient of restitution is the ratio of relative velocity after impact to the relative velocity before impact.

EXPLANATION:

EXPLANATION:
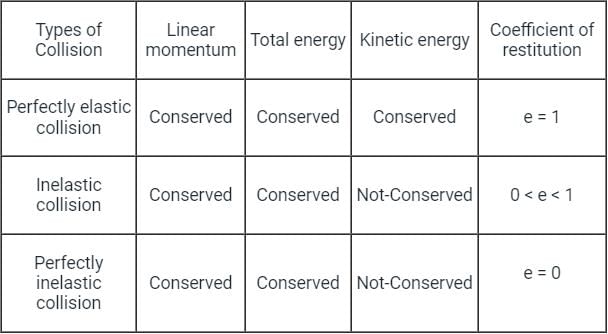
- Perfectly elastic collision: A perfectly elastic collision is defined as one in which there is no loss of kinetic energy and the momentum of the system is conserved in the collision.
- Inelastic or plastic collision: A inelastic collision is defined as one in which there is a loss of kinetic energy and the momentum of the system is conserved in the collision.
- In the plastic collision, the velocity of separation is always less than the velocity of approach
⇒ 0 < e < 1
- Perfectly inelastic collision or plastic collision: A collision between two bodies in which two bodies stick together after collision and then move as one body, is called a perfectly inelastic collision or plastic collision. In this type of interaction, the momentum of the system remains conserved and the loss of kinetic energy is maximum.
- So, for perfectly plastic collisions,
⇒ e = 0
- For perfectly elastic collision, energy is conserved, so the height rebounds by an object are some as the initial height
So, options 1, 3, and 4 are correct.
A 1.0 kg ball drops vertically onto the floor with a speed of 25 m/s. It rebounds with an initial speed of 10 m/s. The impulse action on the ball during contact will be- a)15 N-s
- b)25 N-s
- c)35 N-s
- d)45 N-s
Correct answer is option 'C'. Can you explain this answer?
A 1.0 kg ball drops vertically onto the floor with a speed of 25 m/s. It rebounds with an initial speed of 10 m/s. The impulse action on the ball during contact will be
a)
15 N-s
b)
25 N-s
c)
35 N-s
d)
45 N-s

|
Anisha Chakraborty answered |
Impulse during Contact:
In order to calculate the impulse during the contact between the ball and the floor, we can use the principle of conservation of momentum. The impulse experienced by an object is equal to the change in momentum it undergoes during a collision.
Initial Momentum:
The initial momentum of the ball can be calculated using the formula:
\[p_{initial} = m \times v_{initial}\]
where
m = mass of the ball (1.0 kg)
v_{initial} = initial speed of the ball (25 m/s)
Final Momentum:
The final momentum of the ball can be calculated using the formula:
\[p_{final} = m \times v_{final}\]
where
m = mass of the ball (1.0 kg)
v_{final} = final speed of the ball (10 m/s)
Impulse:
The impulse experienced by the ball during contact is given by the formula:
\[Impulse = p_{final} - p_{initial}\]
Substitute the values into the formula to find the impulse:
\[Impulse = (1.0 \times 10) - (1.0 \times 25) = 10 - 25 = -15\,kg\,m/s\]
The negative sign indicates that the direction of the impulse is opposite to the initial direction of motion. Therefore, the magnitude of the impulse is 15 N-s.
Therefore, the correct answer is option C which is 35 N-s.
In order to calculate the impulse during the contact between the ball and the floor, we can use the principle of conservation of momentum. The impulse experienced by an object is equal to the change in momentum it undergoes during a collision.
Initial Momentum:
The initial momentum of the ball can be calculated using the formula:
\[p_{initial} = m \times v_{initial}\]
where
m = mass of the ball (1.0 kg)
v_{initial} = initial speed of the ball (25 m/s)
Final Momentum:
The final momentum of the ball can be calculated using the formula:
\[p_{final} = m \times v_{final}\]
where
m = mass of the ball (1.0 kg)
v_{final} = final speed of the ball (10 m/s)
Impulse:
The impulse experienced by the ball during contact is given by the formula:
\[Impulse = p_{final} - p_{initial}\]
Substitute the values into the formula to find the impulse:
\[Impulse = (1.0 \times 10) - (1.0 \times 25) = 10 - 25 = -15\,kg\,m/s\]
The negative sign indicates that the direction of the impulse is opposite to the initial direction of motion. Therefore, the magnitude of the impulse is 15 N-s.
Therefore, the correct answer is option C which is 35 N-s.
Moment of inertia of a circular wire of mass M and radius R about its diameter is _______- a)1/2 MR2
- b)1/4 MR2
- c)2MR2
- d)MR2
Correct answer is option 'B'. Can you explain this answer?
Moment of inertia of a circular wire of mass M and radius R about its diameter is _______
a)
1/2 MR2
b)
1/4 MR2
c)
2MR2
d)
MR2
|
|
Neha Joshi answered |
A circular wire behaves like a ring. By perpendicular axes theorem,
ID + ID = 1/2 MR2
Therefore,
1/4 MR2.
ID + ID = 1/2 MR2
Therefore,
1/4 MR2.
During rolling, the force of friction acts in the same direction as the direction of motion of the centre of mass of the body.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
During rolling, the force of friction acts in the same direction as the direction of motion of the centre of mass of the body.
a)
True
b)
False
|
|
Sinjini Nambiar answered |
Understanding Rolling Motion
Rolling motion occurs when an object rotates about an axis while simultaneously translating along a surface. This type of motion is commonly observed in wheels, balls, and cylinders.
The Role of Friction in Rolling
- In rolling motion, the point of contact between the rolling object and the surface does not slide; rather, it is momentarily at rest.
- The force of friction is essential in ensuring that the object rolls without slipping. This frictional force provides the necessary torque for the object to rotate.
Direction of Frictional Force
- In the case of rolling, the frictional force acts in the direction that aids the motion of the center of mass of the body.
- When a rolling object moves forward, friction acts forward, enhancing its translational motion.
Example for Clarity
- Consider a ball rolling down an inclined plane. The frictional force at the contact point acts in the direction of the ball's movement, facilitating both rotation and translation without slipping.
Conclusion
- Therefore, the statement that "the force of friction acts in the same direction as the direction of motion of the center of mass of the body" is indeed true.
- This unique characteristic of friction in rolling is crucial for the efficiency and stability of rolling bodies.
Understanding these dynamics helps in various applications in mechanical engineering, ensuring designs that optimize performance through effective use of rolling motion.
Rolling motion occurs when an object rotates about an axis while simultaneously translating along a surface. This type of motion is commonly observed in wheels, balls, and cylinders.
The Role of Friction in Rolling
- In rolling motion, the point of contact between the rolling object and the surface does not slide; rather, it is momentarily at rest.
- The force of friction is essential in ensuring that the object rolls without slipping. This frictional force provides the necessary torque for the object to rotate.
Direction of Frictional Force
- In the case of rolling, the frictional force acts in the direction that aids the motion of the center of mass of the body.
- When a rolling object moves forward, friction acts forward, enhancing its translational motion.
Example for Clarity
- Consider a ball rolling down an inclined plane. The frictional force at the contact point acts in the direction of the ball's movement, facilitating both rotation and translation without slipping.
Conclusion
- Therefore, the statement that "the force of friction acts in the same direction as the direction of motion of the center of mass of the body" is indeed true.
- This unique characteristic of friction in rolling is crucial for the efficiency and stability of rolling bodies.
Understanding these dynamics helps in various applications in mechanical engineering, ensuring designs that optimize performance through effective use of rolling motion.
The impact is said to be inelastic or plastic when the coefficient of restitution is ________.- a)zero
- b)one
- c)greater than one
- d)0.5
Correct answer is option 'A'. Can you explain this answer?
The impact is said to be inelastic or plastic when the coefficient of restitution is ________.
a)
zero
b)
one
c)
greater than one
d)
0.5
|
|
Sai Reddy answered |
The concept of coefficient of restitution:
The coefficient of restitution (COR) is a measure of the elasticity of a collision between two objects. It is defined as the ratio of the relative velocity of separation after collision to the relative velocity of approach before the collision.
Definition of inelastic or plastic impact:
In an inelastic or plastic impact, the two objects stick together after the collision and move as one. In other words, there is no separation between the objects after the collision, and they have a common final velocity.
Explanation of the impact being inelastic or plastic when the coefficient of restitution is zero:
When the coefficient of restitution is zero, it means that the relative velocity of separation after the collision is zero. This implies that the objects do not separate after the collision and stick together. As a result, the impact is said to be inelastic or plastic.
Example to illustrate the concept:
Consider a ball that is dropped vertically onto a flat surface. When the ball hits the surface, it loses all of its initial velocity and comes to rest momentarily. In this case, the coefficient of restitution is zero because the relative velocity of separation after the collision is zero. The ball and the surface stick together, and the impact is inelastic or plastic.
Conclusion:
When the coefficient of restitution is zero, it indicates that the objects do not separate after the collision and stick together. This type of impact is known as an inelastic or plastic impact.
The coefficient of restitution (COR) is a measure of the elasticity of a collision between two objects. It is defined as the ratio of the relative velocity of separation after collision to the relative velocity of approach before the collision.
Definition of inelastic or plastic impact:
In an inelastic or plastic impact, the two objects stick together after the collision and move as one. In other words, there is no separation between the objects after the collision, and they have a common final velocity.
Explanation of the impact being inelastic or plastic when the coefficient of restitution is zero:
When the coefficient of restitution is zero, it means that the relative velocity of separation after the collision is zero. This implies that the objects do not separate after the collision and stick together. As a result, the impact is said to be inelastic or plastic.
Example to illustrate the concept:
Consider a ball that is dropped vertically onto a flat surface. When the ball hits the surface, it loses all of its initial velocity and comes to rest momentarily. In this case, the coefficient of restitution is zero because the relative velocity of separation after the collision is zero. The ball and the surface stick together, and the impact is inelastic or plastic.
Conclusion:
When the coefficient of restitution is zero, it indicates that the objects do not separate after the collision and stick together. This type of impact is known as an inelastic or plastic impact.
A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination. In each case, the ball will ______- a)Reach the bottom at the same time
- b)Will take longer time to roll down one plane
- c)Reach the bottom at an unpredictable time
- d)Reach the bottom at the same time and keeps rolling
Correct answer is option 'B'. Can you explain this answer?
A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination. In each case, the ball will ______
a)
Reach the bottom at the same time
b)
Will take longer time to roll down one plane
c)
Reach the bottom at an unpredictable time
d)
Reach the bottom at the same time and keeps rolling
|
|
Neha Joshi answered |
Acceleration of the rolling sphere,
a = gsinθ/((1+k2/R2))
Velocity of the sphere at the bottom of the inclined plane,
v = √(2gh/((1+k2/R2)))
The sphere will take a longer time to roll down one plane than the other. It will take a larger time in case if the plane with smaller inclination because the acceleration is proportional to sinθ.
a = gsinθ/((1+k2/R2))
Velocity of the sphere at the bottom of the inclined plane,
v = √(2gh/((1+k2/R2)))
The sphere will take a longer time to roll down one plane than the other. It will take a larger time in case if the plane with smaller inclination because the acceleration is proportional to sinθ.
Calculate the velocity of a body having a mass of 9 kg and linear momentum of 63 kg m/s.- a)6 m/s
- b)7 m/s
- c)8 m/s
- d)10 m/s
Correct answer is option 'B'. Can you explain this answer?
Calculate the velocity of a body having a mass of 9 kg and linear momentum of 63 kg m/s.
a)
6 m/s
b)
7 m/s
c)
8 m/s
d)
10 m/s
|
|
Neha Joshi answered |
Linear momentum:
- It is the product of the mass and velocity of an object.
- Like velocity, linear momentum is a vector quantity possessing a direction as well as magnitude.
P = mv
where P = momentum and v = velovity.
Calculation:
Given:
Mass = 9 kg, P = 63 kg-m/sec
P = mv
63 = 9 × v
v = 7 m/s
where P = momentum and v = velovity.
Calculation:
Given:
Mass = 9 kg, P = 63 kg-m/sec
P = mv
63 = 9 × v
v = 7 m/s
During inelastic collision of two particles, which one of the following is conserved ?- a)total linear momentum only
- b)total kinetic energy only
- c)both linear momentum and kinetic energy
- d)neither linear momentum nor kinetic energy
Correct answer is option 'A'. Can you explain this answer?
During inelastic collision of two particles, which one of the following is conserved ?
a)
total linear momentum only
b)
total kinetic energy only
c)
both linear momentum and kinetic energy
d)
neither linear momentum nor kinetic energy

|
Srestha Datta answered |
Conservation of Linear Momentum in Inelastic Collisions
In an inelastic collision, two particles collide and stick together, resulting in a loss of kinetic energy. During this type of collision, the total linear momentum is conserved, but the total kinetic energy is not conserved.
Definition of Linear Momentum
Linear momentum is a vector quantity that depends on the mass and velocity of an object. Mathematically, it is given by the product of mass and velocity:
Momentum (p) = mass (m) * velocity (v)
Conservation of Linear Momentum
According to Newton's third law of motion, the total linear momentum of an isolated system remains constant before and after the collision, provided no external forces act on the system. This principle is known as the conservation of linear momentum.
In an inelastic collision, the two particles collide and stick together, forming a single object. Since the particles stick together, they move with the same final velocity after the collision. As a result, the total momentum of the system before and after the collision remains the same.
Mathematical Representation
Let's consider two particles with masses m1 and m2, initially moving with velocities u1 and u2, respectively. After the collision, they stick together and move with a final velocity v. The conservation of linear momentum can be expressed as follows:
Initial momentum = Final momentum
(m1 * u1) + (m2 * u2) = (m1 + m2) * v
Conservation of Kinetic Energy
In an inelastic collision, the total kinetic energy of the system before the collision is not equal to the total kinetic energy after the collision. Some kinetic energy is lost during the collision, typically transforming into other forms of energy such as heat, sound, or deformation.
This loss of kinetic energy is primarily due to the fact that the two particles stick together instead of bouncing off each other. The energy required to permanently deform the particles or overcome intermolecular forces results in a decrease in kinetic energy.
Conclusion
In summary, during an inelastic collision of two particles, the total linear momentum is conserved, but the total kinetic energy is not conserved. This is because the particles stick together and move with a common final velocity, resulting in a loss of kinetic energy.
In an inelastic collision, two particles collide and stick together, resulting in a loss of kinetic energy. During this type of collision, the total linear momentum is conserved, but the total kinetic energy is not conserved.
Definition of Linear Momentum
Linear momentum is a vector quantity that depends on the mass and velocity of an object. Mathematically, it is given by the product of mass and velocity:
Momentum (p) = mass (m) * velocity (v)
Conservation of Linear Momentum
According to Newton's third law of motion, the total linear momentum of an isolated system remains constant before and after the collision, provided no external forces act on the system. This principle is known as the conservation of linear momentum.
In an inelastic collision, the two particles collide and stick together, forming a single object. Since the particles stick together, they move with the same final velocity after the collision. As a result, the total momentum of the system before and after the collision remains the same.
Mathematical Representation
Let's consider two particles with masses m1 and m2, initially moving with velocities u1 and u2, respectively. After the collision, they stick together and move with a final velocity v. The conservation of linear momentum can be expressed as follows:
Initial momentum = Final momentum
(m1 * u1) + (m2 * u2) = (m1 + m2) * v
Conservation of Kinetic Energy
In an inelastic collision, the total kinetic energy of the system before the collision is not equal to the total kinetic energy after the collision. Some kinetic energy is lost during the collision, typically transforming into other forms of energy such as heat, sound, or deformation.
This loss of kinetic energy is primarily due to the fact that the two particles stick together instead of bouncing off each other. The energy required to permanently deform the particles or overcome intermolecular forces results in a decrease in kinetic energy.
Conclusion
In summary, during an inelastic collision of two particles, the total linear momentum is conserved, but the total kinetic energy is not conserved. This is because the particles stick together and move with a common final velocity, resulting in a loss of kinetic energy.
A ball 'A' of mass 'm' falls under gravity from a height 'h' and strikes another ball 'B' of mass 'm' which supported at rest on a spring of stiffness 'k' . Assume perfectly elastic impact . Immediately after the impact,- a)Velocity of ball A is ( 1/2.√2gh )
- b)Velocity of ball A is zero
- c)Velocity of both balls are( 1/2 .√ 2.gh )
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
A ball 'A' of mass 'm' falls under gravity from a height 'h' and strikes another ball 'B' of mass 'm' which supported at rest on a spring of stiffness 'k' . Assume perfectly elastic impact . Immediately after the impact,
a)
Velocity of ball A is ( 1/2.√2gh )
b)
Velocity of ball A is zero
c)
Velocity of both balls are( 1/2 .√ 2.gh )
d)
None of the above
|
|
Neha Joshi answered |
Concept:
In perfectly elastic collision, both the balls will interchange their velocity after impact, i.e. velocity of ball A after impact = 0
In perfectly elastic collision, both the balls will interchange their velocity after impact, i.e. velocity of ball A after impact = 0
Important Point
Coefficient of restitution,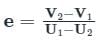
1 = before impact, 2 = after impact
For perfectly elastic body, e = 1
For perfectly plastic body, e = 0
Coefficient of restitution,
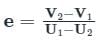
1 = before impact, 2 = after impact
For perfectly elastic body, e = 1
For perfectly plastic body, e = 0
One solid sphere ‘A’ and another hollow sphere ‘B’ are of same mass and same outer radii. Their moments of inertia about their diameters are respectively IA and IB, such that _____________- a)IA=IB
- b)IA is greater thab IB
- c)IA is lesser than IB
- d)IA/IB =ρA/ρB
Correct answer is option 'C'. Can you explain this answer?
One solid sphere ‘A’ and another hollow sphere ‘B’ are of same mass and same outer radii. Their moments of inertia about their diameters are respectively IA and IB, such that _____________
a)
IA=IB
b)
IA is greater thab IB
c)
IA is lesser than IB
d)
IA/IB =ρA/ρB
|
|
Athul Kumar answered |
Introduction
In this discussion, we analyze the moments of inertia of a solid sphere ‘A’ and a hollow sphere ‘B’, both having the same mass and outer radius.
Moments of Inertia
- The moment of inertia (I) is a measure of an object's resistance to rotational motion about an axis.
- For a solid sphere:
- IA = (2/5) * m * R^2
- Here, m is the mass and R is the radius of the solid sphere.
- For a hollow sphere:
- IB = (2/3) * m * R^2
- This formula applies to a thin-walled hollow sphere.
Comparison of IA and IB
- To compare IA and IB, we can substitute the formulas derived:
- IA = (2/5) * m * R^2
- IB = (2/3) * m * R^2
- When comparing these, we see:
- (2/5) < (2/3)="" />
Conclusion
- Therefore, it follows that:
- IA < />
- This indicates that the moment of inertia of the solid sphere is less than that of the hollow sphere.
Final Answer
- The correct answer is option 'C': IA is lesser than IB.
This conclusion arises from the fundamental differences in mass distribution between a solid sphere and a hollow sphere, leading to different resistances to rotational motion.
In this discussion, we analyze the moments of inertia of a solid sphere ‘A’ and a hollow sphere ‘B’, both having the same mass and outer radius.
Moments of Inertia
- The moment of inertia (I) is a measure of an object's resistance to rotational motion about an axis.
- For a solid sphere:
- IA = (2/5) * m * R^2
- Here, m is the mass and R is the radius of the solid sphere.
- For a hollow sphere:
- IB = (2/3) * m * R^2
- This formula applies to a thin-walled hollow sphere.
Comparison of IA and IB
- To compare IA and IB, we can substitute the formulas derived:
- IA = (2/5) * m * R^2
- IB = (2/3) * m * R^2
- When comparing these, we see:
- (2/5) < (2/3)="" />
Conclusion
- Therefore, it follows that:
- IA < />
- This indicates that the moment of inertia of the solid sphere is less than that of the hollow sphere.
Final Answer
- The correct answer is option 'C': IA is lesser than IB.
This conclusion arises from the fundamental differences in mass distribution between a solid sphere and a hollow sphere, leading to different resistances to rotational motion.
A 2 m long alloy bar of 1500 mm2 cross-sectional area hangs vertically and has a collar securely fixed at its lower end. What is the stress-induced in the bar when a weight of 2 kN falls from a height of 100 mm on the collar? (Take E = 120 GPa)- a)126.5 MPa
- b)158.3 MPa
- c)161.2 MPa
- d)181.3 MPa
Correct answer is option 'A'. Can you explain this answer?
A 2 m long alloy bar of 1500 mm2 cross-sectional area hangs vertically and has a collar securely fixed at its lower end. What is the stress-induced in the bar when a weight of 2 kN falls from a height of 100 mm on the collar? (Take E = 120 GPa)
a)
126.5 MPa
b)
158.3 MPa
c)
161.2 MPa
d)
181.3 MPa
|
|
Neha Joshi answered |
Given Data:
Length of bar(l)= 2 m
Cross-sectional Area of bar(A)= 1500 mm2
Weight of fall on collar of bar(P)= 2 kN= 2000 N
Height from which weigh falls(h)= 100 mm
Modulus of Elasticity(E)= 120 GPa = 120 x 1000 N/mm2
Explanation:
Stress-induced due to the load is applied with impact:
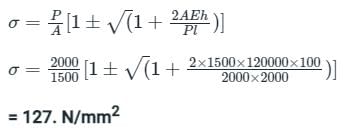
Additional Information
Stress-induced due to the load is applied with impact:
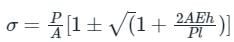
where Length of the bar(l), Cross-sectional Area of the bar(A), Weight of fall on the collar of the bar(P)'
Height from which weight falls(h), Modulus of Elasticity(E)
Case- When Deformation is very small as compared to h, Then
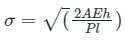
Length of bar(l)= 2 m
Cross-sectional Area of bar(A)= 1500 mm2
Weight of fall on collar of bar(P)= 2 kN= 2000 N
Height from which weigh falls(h)= 100 mm
Modulus of Elasticity(E)= 120 GPa = 120 x 1000 N/mm2
Explanation:
Stress-induced due to the load is applied with impact:
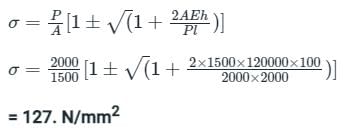
Additional Information
Stress-induced due to the load is applied with impact:
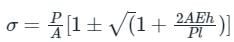
where Length of the bar(l), Cross-sectional Area of the bar(A), Weight of fall on the collar of the bar(P)'
Height from which weight falls(h), Modulus of Elasticity(E)
Case- When Deformation is very small as compared to h, Then
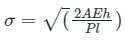
A hook of radius 2m weighs 100kg. It rolls along a horizontal floor so that its centre if mass has a speed of 20cm/s. How much work has to be done to stop it?- a)5 J
- b)6 J
- c)2 J
- d)4 J
Correct answer is option 'D'. Can you explain this answer?
A hook of radius 2m weighs 100kg. It rolls along a horizontal floor so that its centre if mass has a speed of 20cm/s. How much work has to be done to stop it?
a)
5 J
b)
6 J
c)
2 J
d)
4 J

|
Sagnik Sen answered |
To find the work done to stop the hook, we need to consider the energy involved. The hook has kinetic energy due to its motion, and work is done to stop it by removing this kinetic energy.
Given:
- Radius of the hook, r = 2m
- Mass of the hook, m = 100kg
- Speed of the center of mass, v = 20cm/s = 0.2m/s
1. Find the kinetic energy of the hook:
The kinetic energy of an object is given by the formula:
KE = (1/2)mv^2
Substituting the given values:
KE = (1/2)(100kg)(0.2m/s)^2
KE = 2J
2. Find the work done to stop the hook:
The work done is equal to the change in kinetic energy. Since the hook is brought to rest, the change in kinetic energy is equal to the initial kinetic energy.
Work done = Change in kinetic energy = KE = 2J
Therefore, the work done to stop the hook is 2J.
Final Answer:
The correct answer is option D) 4 J.
Given:
- Radius of the hook, r = 2m
- Mass of the hook, m = 100kg
- Speed of the center of mass, v = 20cm/s = 0.2m/s
1. Find the kinetic energy of the hook:
The kinetic energy of an object is given by the formula:
KE = (1/2)mv^2
Substituting the given values:
KE = (1/2)(100kg)(0.2m/s)^2
KE = 2J
2. Find the work done to stop the hook:
The work done is equal to the change in kinetic energy. Since the hook is brought to rest, the change in kinetic energy is equal to the initial kinetic energy.
Work done = Change in kinetic energy = KE = 2J
Therefore, the work done to stop the hook is 2J.
Final Answer:
The correct answer is option D) 4 J.
During elastic and inelastic collision, ________ is conserved.- a)kinetic energy
- b)velocity
- c)viscosity
- d)momentum
Correct answer is option 'D'. Can you explain this answer?
During elastic and inelastic collision, ________ is conserved.
a)
kinetic energy
b)
velocity
c)
viscosity
d)
momentum
|
|
Atharva Majumdar answered |
Conservation of Momentum in Elastic and Inelastic Collisions
In both elastic and inelastic collisions, momentum is conserved. This means that the total momentum of the system before the collision is equal to the total momentum of the system after the collision.
Elastic Collision
- In an elastic collision, kinetic energy is also conserved along with momentum.
- The objects bounce off each other without any loss of kinetic energy.
- The total kinetic energy before the collision is equal to the total kinetic energy after the collision.
Inelastic Collision
- In an inelastic collision, kinetic energy is not conserved.
- Some of the kinetic energy is transformed into other forms of energy like sound, heat, or deformation of the objects.
- Despite this loss of kinetic energy, momentum is still conserved in the system.
Explanation
- Momentum is conserved in collisions because there is no external force acting on the system during the collision.
- According to Newton's third law of motion, the forces between the objects in the collision are equal and opposite, resulting in a constant total momentum.
- This conservation of momentum is a fundamental principle in physics and is used to analyze and predict the behavior of objects in collisions.
Therefore, in both elastic and inelastic collisions, momentum is conserved, making it a crucial concept in understanding the dynamics of interactions between objects.
In both elastic and inelastic collisions, momentum is conserved. This means that the total momentum of the system before the collision is equal to the total momentum of the system after the collision.
Elastic Collision
- In an elastic collision, kinetic energy is also conserved along with momentum.
- The objects bounce off each other without any loss of kinetic energy.
- The total kinetic energy before the collision is equal to the total kinetic energy after the collision.
Inelastic Collision
- In an inelastic collision, kinetic energy is not conserved.
- Some of the kinetic energy is transformed into other forms of energy like sound, heat, or deformation of the objects.
- Despite this loss of kinetic energy, momentum is still conserved in the system.
Explanation
- Momentum is conserved in collisions because there is no external force acting on the system during the collision.
- According to Newton's third law of motion, the forces between the objects in the collision are equal and opposite, resulting in a constant total momentum.
- This conservation of momentum is a fundamental principle in physics and is used to analyze and predict the behavior of objects in collisions.
Therefore, in both elastic and inelastic collisions, momentum is conserved, making it a crucial concept in understanding the dynamics of interactions between objects.
During Perfectly Elastic Collision between two bodies, which of the following quantities always remains conserved?- a)Total Kinetic Energy
- b)Total Linear Momentum
- c)Both total kinetic energy and linear momentum
- d)Neither Kinetic energy nor linear momentum
Correct answer is option 'C'. Can you explain this answer?
During Perfectly Elastic Collision between two bodies, which of the following quantities always remains conserved?
a)
Total Kinetic Energy
b)
Total Linear Momentum
c)
Both total kinetic energy and linear momentum
d)
Neither Kinetic energy nor linear momentum
|
|
Neha Joshi answered |
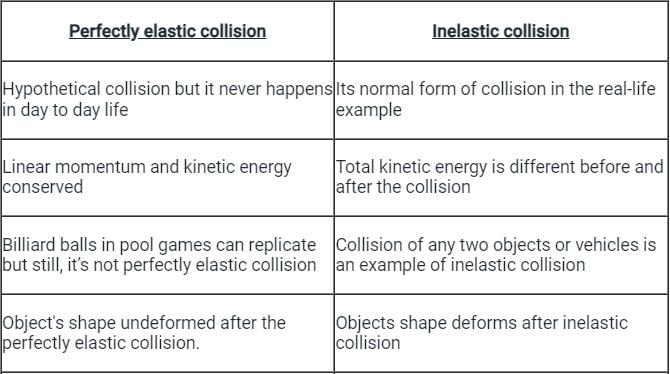
The correct answer is Both total kinetic energy and total linear momentum
- A perfectly inelastic collision is a hypothetical collision in which two objects collide and energy is not wasted and momentum is conserved.
- While Perfectly elastic collision happens then the object’s shape remains unchanged or not deformed.
- Most of the collisions in daily life are inelastic in nature.
Important Points

The impact is said to be inelastic or plastic when the coefficient of restitution is ________.- a)zero
- b)one
- c)greater than one
- d)0.5
Correct answer is option 'A'. Can you explain this answer?
The impact is said to be inelastic or plastic when the coefficient of restitution is ________.
a)
zero
b)
one
c)
greater than one
d)
0.5
|
|
Neha Joshi answered |
- Momentum is conserved in all collisions.
- In elastic collision, kinetic energy is also conserved.
- In inelastic collision, kinetic energy is not conserved. In a perfectly inelastic collision, objects stick together after the collision.
Perfectly elastic collision:
If the law of conservation of momentum and that of kinetic energy hold good during the collision.
If the law of conservation of momentum and that of kinetic energy hold good during the collision.
Inelastic collision:
Law of conservation of momentum holds good during a collision while that of kinetic energy is not conserved.
Coefficient of restitution (e)
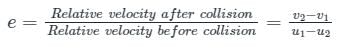
Law of conservation of momentum holds good during a collision while that of kinetic energy is not conserved.
Coefficient of restitution (e)
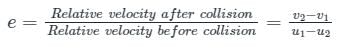
- For perfectly elastic collision, e = 1
- For inelastic collision, e < 1
- For perfectly inelastic collision, e = 0
Two particles A and B, initially at rest, move towards each other under mutual force of attraction. At the instant when the speed of A is v and the speed of B is 2v, what is the speed of mass of the system?- a)3v
- b)v
- c)Zero
- d)1.5v
Correct answer is option 'C'. Can you explain this answer?
Two particles A and B, initially at rest, move towards each other under mutual force of attraction. At the instant when the speed of A is v and the speed of B is 2v, what is the speed of mass of the system?
a)
3v
b)
v
c)
Zero
d)
1.5v
|
|
Neha Joshi answered |
No external force is acting on the centre of mass. It remains at rest. The speed of centre of mass is zero.
The rate of change of momentum is equal to the applied force and it takes place in the direction of the force is a statement of:- a)Continuity equation
- b)Pascal’s equation
- c)Impulse – Momentum equation
- d)Darcy’s equation
Correct answer is option 'C'. Can you explain this answer?
The rate of change of momentum is equal to the applied force and it takes place in the direction of the force is a statement of:
a)
Continuity equation
b)
Pascal’s equation
c)
Impulse – Momentum equation
d)
Darcy’s equation
|
|
Neha Joshi answered |
Newton’s Second law of motion: The rate of change of momentum of any object is directly proportional to the applied force on the body.
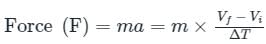
F × ΔT = ΔP
Where Δ P = Change in momentum and Δ T = change in time taken
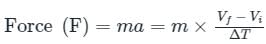
F × ΔT = ΔP
Where Δ P = Change in momentum and Δ T = change in time taken
- The above equation is known as Impulse Momentum equation and states that the impulse or force intensity is equal to change in momentum.
- According to the impulse-momentum equation, the change in momentum of an object depends on both the net force acting on the object and duration of the net force.
A child sits stationary at one end of a long trolley moving uniformly with speed v on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, then what is the effect of the speed of the centre of mass of the (trolley+child) system?- a)The speed of the centre of mass increases
- b)The speed of the centre of mass decreases
- c)The speed of the centre of mass will not change
- d)The speed of the centre of mass will first increase and then decrease
Correct answer is option 'C'. Can you explain this answer?
A child sits stationary at one end of a long trolley moving uniformly with speed v on a smooth horizontal floor. If the child gets up and runs about on the trolley in any manner, then what is the effect of the speed of the centre of mass of the (trolley+child) system?
a)
The speed of the centre of mass increases
b)
The speed of the centre of mass decreases
c)
The speed of the centre of mass will not change
d)
The speed of the centre of mass will first increase and then decrease
|
|
Neha Joshi answered |
The force involved in the given problem is the internal forces of the system. No external force acts on the system when the child runs So, there will be no change in the speed of the centre of mass of the (trolley+child) system.
A smooth sphere A is moving on a frictionless horizontal plane with angular speed ω and the centre of mass velocity u. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ω(A) and ω(B) respectively. Then?- a)ωA is lesser than ωB
- b)ωA = ωB
- c)ωA = ω
- d)ωB = ω
Correct answer is option 'C'. Can you explain this answer?
A smooth sphere A is moving on a frictionless horizontal plane with angular speed ω and the centre of mass velocity u. It collides elastically and head on with an identical sphere B at rest. Neglect friction everywhere. After the collision, their angular speeds are ω(A) and ω(B) respectively. Then?
a)
ωA is lesser than ωB
b)
ωA = ωB
c)
ωA = ω
d)
ωB = ω
|
|
Neha Joshi answered |
Only their linear velocities are exchanged. The two spheres cannot exert torques on each other, as their surfaces are frictionless, and so that angular velocities of the sphere do not change.
Where does the centre of mass of two particles of an equal mass lie?- a)Inside the body
- b)Outside the body
- c)Near the first body
- d)Midway between them
Correct answer is option 'D'. Can you explain this answer?
Where does the centre of mass of two particles of an equal mass lie?
a)
Inside the body
b)
Outside the body
c)
Near the first body
d)
Midway between them
|
|
Neha Joshi answered |
The centre of mass of two particles of equal masses lies midway between them. Its position vector is the average of the position vectors of the two particles.
Two balls of equal mass and of Perfectly elastic material are lying on the floor. One of the balls with velocity V is made to strike the second ball. Both the balls after impact will move with a velocity- a)v
- b)v/2
- c)v/4
- d)v/8
Correct answer is option 'B'. Can you explain this answer?
Two balls of equal mass and of Perfectly elastic material are lying on the floor. One of the balls with velocity V is made to strike the second ball. Both the balls after impact will move with a velocity
a)
v
b)
v/2
c)
v/4
d)
v/8
|
|
Neha Joshi answered |
This is the perfectly inelastic collision/impact of the case of two bodies/balls as both the balls stick after the collision.
Perfect Inelastic Collision:
Perfect Inelastic Collision:
- Two bodies move together with the same velocity.
- The coefficient of Restitution will be 0.
- Momentum is Conserved.
- Kinetic Energy will not be Conserved.
Calculation:
Given:
Let two balls A and B have mass mA, mB respectively, and their initial velocities are uA and uB. After the collision, they will move with the same velocity, vo.
Given that mass of both balls are same.
So mA = mB = m
uA = V, uB = 0
From the Concept of Momentum Conservation:
mAuA + mBuB = (m+m)vo
mV = 2mvo
vo = V/2
Both the balls after impact will move with velocity v/2.
Given:
Let two balls A and B have mass mA, mB respectively, and their initial velocities are uA and uB. After the collision, they will move with the same velocity, vo.
Given that mass of both balls are same.
So mA = mB = m
uA = V, uB = 0
From the Concept of Momentum Conservation:
mAuA + mBuB = (m+m)vo
mV = 2mvo
vo = V/2
Both the balls after impact will move with velocity v/2.
If u1 and u2 are the velocities of two moving bodies in the same direction before impact and V1 and V2 are their velocities after impact, then coefficient of restitution is given by- a)
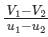
- b)
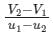
- c)
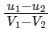
- d)
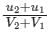
Correct answer is option 'B'. Can you explain this answer?
If u1 and u2 are the velocities of two moving bodies in the same direction before impact and V1 and V2 are their velocities after impact, then coefficient of restitution is given by
a)
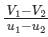
b)
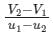
c)
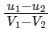
d)
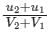
|
|
Neha Joshi answered |
Coefficient of restitution (e):
The coefficient of restitution or coefficient of the resilience of a collision is defined as the ratio of the relative velocity of separation after the collision to the relative velocity of an approach before the collision.
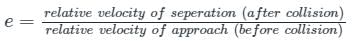
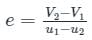
Properties of different types of collision are given in the table below:
The coefficient of restitution or coefficient of the resilience of a collision is defined as the ratio of the relative velocity of separation after the collision to the relative velocity of an approach before the collision.
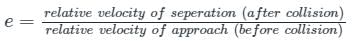
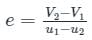
Properties of different types of collision are given in the table below:

If the momentum of a body increases from 10 units to 25 units in 5 sec, then the force acting on it is- a)1 unit
- b)2 units
- c)3 units
- d)4 units
Correct answer is option 'C'. Can you explain this answer?
If the momentum of a body increases from 10 units to 25 units in 5 sec, then the force acting on it is
a)
1 unit
b)
2 units
c)
3 units
d)
4 units
|
|
Neha Joshi answered |
The correct answer is 3 units.
- Newton's 2nd law of motion says the rate change of momentum is called force.
- The equation for the change in momentum is F × t = m × Δv
- If the momentum of a body increases from 10 units to 25 units in 5 seconds.
- Then the change in the momentum is 25 – 10 = 15 units in time 5 seconds.
- So the Force extract from this is 15/5 = 3 Newton.
Key Points
- Momentum is a vector quantity that is the product of the mass (weight) of a particle and its velocity (speed).
- SI unit: kilogram meter per second (kg⋅m/s).
- A spinning object has angular momentum.
- An object travelling with a velocity has linear momentum.
- A change in momentum may result from an acceleration or a force or an impulse.
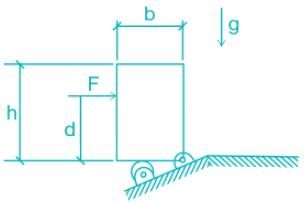
A rigid homogeneous uniform block of mass 1 kg, height h = 0.4 m and width b = 0.3 m is pinned at one corner and placed upright in a uniform gravitational field (g = 9.81 m/s2), supported by a roller in the configuration shown in the figure. A short duration (impulsive) force F, producing an impulse IF is applied at a height of d = 0.3 m from the bottom as shown. Assume all joints to be frictionless. The minimum value of IF required to topple the block is
- a)0.953 Ns
- b)1.403 Ns
- c)0.814 Ns
- d)1.172 Ns
Correct answer is option 'A'. Can you explain this answer?
A rigid homogeneous uniform block of mass 1 kg, height h = 0.4 m and width b = 0.3 m is pinned at one corner and placed upright in a uniform gravitational field (g = 9.81 m/s2), supported by a roller in the configuration shown in the figure. A short duration (impulsive) force F, producing an impulse IF is applied at a height of d = 0.3 m from the bottom as shown. Assume all joints to be frictionless. The minimum value of IF required to topple the block is


a)
0.953 Ns
b)
1.403 Ns
c)
0.814 Ns
d)
1.172 Ns
|
|
Neha Joshi answered |
To topple the block we need an impulse force such that the weight will generate a clockwise moment about point O.
This will happen only when a minimum impulse that can rotate the block such that the Centre of gravity of the body will pass through the point O or beyond.
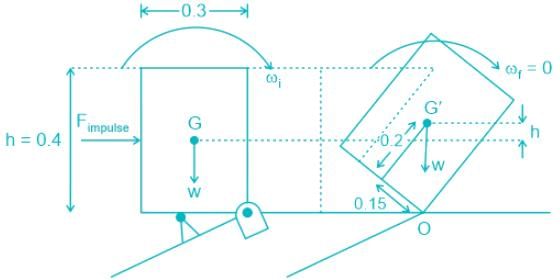
h = 0.4m, b = 0.3 m, m =1kg
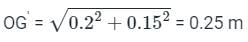
h' = OG' - h/2 = 0.25 - 0.2 = 0.05 m
Due to force F, the block will topple about A
So By energy balance

ω2 = 2 × 12 × 9.81 × 0.05
ω = 3.43 rad/s
Now,
Angular impulse = change in angular momentum
IF × d = Io × (ωi - ωf)
IF × 0.3 = 1/12 × ( 3.43 - 0)
IF = 0.953 Ns
This will happen only when a minimum impulse that can rotate the block such that the Centre of gravity of the body will pass through the point O or beyond.

h = 0.4m, b = 0.3 m, m =1kg
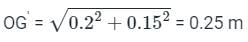
h' = OG' - h/2 = 0.25 - 0.2 = 0.05 m
Due to force F, the block will topple about A
So By energy balance

ω2 = 2 × 12 × 9.81 × 0.05
ω = 3.43 rad/s
Now,
Angular impulse = change in angular momentum
IF × d = Io × (ωi - ωf)
IF × 0.3 = 1/12 × ( 3.43 - 0)
IF = 0.953 Ns
A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination. In each case, the ball will reach the bottom _____- a)With the same speed
- b)With different speed
- c)With different speed but same time
- d)Immediately
Correct answer is option 'A'. Can you explain this answer?
A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination. In each case, the ball will reach the bottom _____
a)
With the same speed
b)
With different speed
c)
With different speed but same time
d)
Immediately
|
|
Neha Joshi answered |
Acceleration of the rolling sphere,
a = gsinθ/((1+k2/R2))
Velocity of the sphere at the bottom of the inclined plane,
v = √(2gh/((1+k2/R2)))
The sphere will reach the bottom with the same speed v because h is the same in both the cases.
a = gsinθ/((1+k2/R2))
Velocity of the sphere at the bottom of the inclined plane,
v = √(2gh/((1+k2/R2)))
The sphere will reach the bottom with the same speed v because h is the same in both the cases.
Chapter doubts & questions for Impulse, Momentum & Collision - Engineering Mechanics 2025 is part of Civil Engineering (CE) exam preparation. The chapters have been prepared according to the Civil Engineering (CE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Impulse, Momentum & Collision - Engineering Mechanics in English & Hindi are available as part of Civil Engineering (CE) exam.
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Engineering Mechanics
23 videos|61 docs|53 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup









