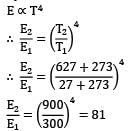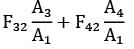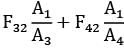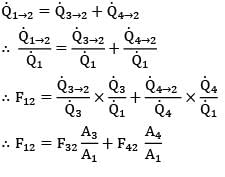All Exams >
Mechanical Engineering >
Heat Transfer >
All Questions
All questions of Radiation for Mechanical Engineering Exam
Two grey surfaces that form an enclosure exchange heat with one another by thermal radiation. Surface 1 has a temperature of 400 K, an area of and a total emissivity of 0.4. Surface 2 has a temperature of 600 K, area of and a total emissivity of 0.6. If the view factor is 0.3, the rate of radiation heat transfer between the two surfaces is- a)135 W
- b)223 W
- c)296 W
- d)342 W
Correct answer is option 'B'. Can you explain this answer?
Two grey surfaces that form an enclosure exchange heat with one another by thermal radiation. Surface 1 has a temperature of 400 K, an area of and a total emissivity of 0.4. Surface 2 has a temperature of 600 K, area of and a total emissivity of 0.6. If the view factor is 0.3, the rate of radiation heat transfer between the two surfaces is
a)
135 W
b)
223 W
c)
296 W
d)
342 W
|
|
Sarita Yadav answered |
Using thermal circuit, the net heat exchange between two surfaces is
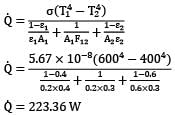
Q = 223.36 W
Consider a surface at 0oC that may be assumed to be a blackbody in an environment at . If of radiation is incident on the surface, the radiosity of this black surface is- a)0 W/m2
- b)15 w/m2
- c)314.94 W/m2
- d)300 W/m2
Correct answer is option 'C'. Can you explain this answer?
Consider a surface at 0oC that may be assumed to be a blackbody in an environment at . If of radiation is incident on the surface, the radiosity of this black surface is
a)
0 W/m2
b)
15 w/m2
c)
314.94 W/m2
d)
300 W/m2
|
|
Sarita Yadav answered |
By definition radiosity is the rate at which a thermal radiation levels a surface per unit area
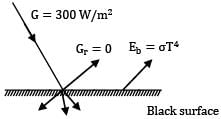
Ga = 300 W/m2
As surface is black, it completely absorbs the radiation incident on it,
Therefore
Gr = 0
By Stefan Boltzmann Law
Eb = σT4
= 5.67 x 10-8 x 2734
Eb = 314.94 W/m2
Radiosity is given as
J = Eb +Gr
J = 314.94 W/m2
Note that Eb>G because the difference Eb - Ga must be equal to rate of heat convection from the environment to surface.
Solar radiation of falls on a grey opaque surface at steady state. The surface has a temperature of and emissivity of 0.8. Find radiosity from the surface?Correct answer is 'A'. Can you explain this answer?
Solar radiation of falls on a grey opaque surface at steady state. The surface has a temperature of and emissivity of 0.8. Find radiosity from the surface?

|
Telecom Tuners answered |
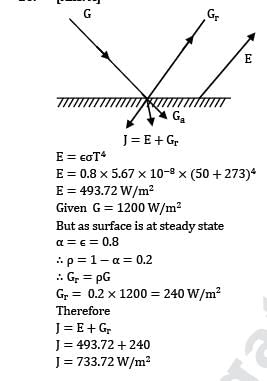
J = E+Gr
E = εσT4
E = 0.8 x 5.67 x 10-8 x (50 + 273)4
E = 493.72 W/m2
Given G = 1200 W/m2
But as surface is at steady state
α = ε = 0.8
∴ ρ = 1 -α = 0.2
∴ Gr = ρG
Gr = 0.2 x 1200 = 240 W/m2
Therefore
J = E+Gr
J = 493.72 + 240
J = 733.72 W/m2
The minimum number of view factors that need to be known to solve a 10-surface enclosure completely, is- a)1
- b)10
- c)22
- d)45
Correct answer is option 'D'. Can you explain this answer?
The minimum number of view factors that need to be known to solve a 10-surface enclosure completely, is
a)
1
b)
10
c)
22
d)
45
|
|
Sarita Yadav answered |
For n-surface enclosure if nC2 view factors are known directly, entire enclosure can be solved. Thus for 10 surfaces, number of view factors that need to be evaluated directly will be
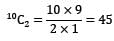
Two infinitely long cylinders are placed coaxially. The inner cylinder has an outside diameter of 7.5 cm, and emissivity of 0.1 and is maintained at 1050 K. The outer cylinder has an inside diameter of 22.5 cm, an emissivity of 0.2 and is maintained at 315 K. A cylindrical shield (very thin so that its temperature is the same on both sides) is placed concentrically midway between the two cylinders and allowed to come to thermal equilibrium. It has an emissivity of 0.3 on both sides. Assuming that vacuum exists between the annular spaces. Find the steady state temperature attained by the cylindrical shield.- a)715.0
- b)718.0
Correct answer is option 'A'. Can you explain this answer?
Two infinitely long cylinders are placed coaxially. The inner cylinder has an outside diameter of 7.5 cm, and emissivity of 0.1 and is maintained at 1050 K. The outer cylinder has an inside diameter of 22.5 cm, an emissivity of 0.2 and is maintained at 315 K. A cylindrical shield (very thin so that its temperature is the same on both sides) is placed concentrically midway between the two cylinders and allowed to come to thermal equilibrium. It has an emissivity of 0.3 on both sides. Assuming that vacuum exists between the annular spaces. Find the steady state temperature attained by the cylindrical shield.
a)
715.0
b)
718.0
|
|
Sarita Yadav answered |
Since the shield is placed midway between both the cylinders, therefore diameter of the shield
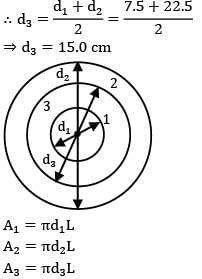
∴ d3 = d1+d2/2 = 7.5 + 22.5/2
⇒ d3 = 15.0 cm
A1 = πd1L
A2 = πd2L
A3 = πd3L
For the system to be steady,
(Q1➝3)net = (Q3➝2)net
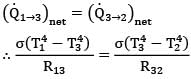
By thermal circuits
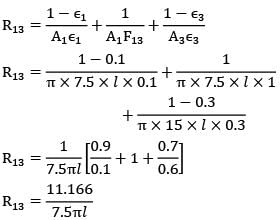
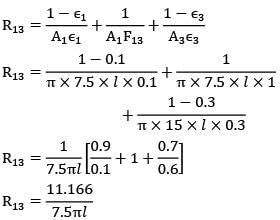
R13 = 11.166/7.5πl
Similarly,
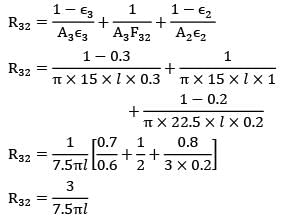
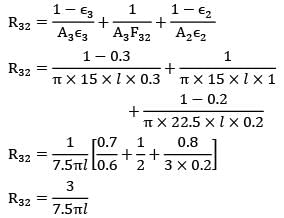
R32 = 3/7.5πl
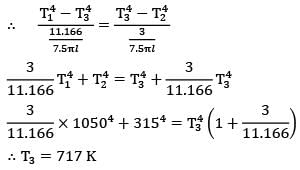
∴ T3 = 717 K
Question_type 5
For an opaque plane surface at steady state the irradiation, radiosity and emissive power are respectively 20, 12 and . What is the emissivity of the surface?- a)0.9
- b)0.4
- c)0.8
- d)1.0
Correct answer is option 'A'. Can you explain this answer?
For an opaque plane surface at steady state the irradiation, radiosity and emissive power are respectively 20, 12 and . What is the emissivity of the surface?
a)
0.9
b)
0.4
c)
0.8
d)
1.0

|
Telecom Tuners answered |
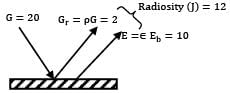
J = pG + εEb
For an opaque body
∵ α + ρ = 1
ρ = 1- α
∴ J = (1-α)G + εEb
By kirchoff’s law, α = ε
∴ J = (1-α)G + εEb
12 = (1- ε)20 + 10
ε = 0.9
Two radiating surfaces A1= 6m2 and A2=4m2 have shape factor Then shape factor will be- a)0.18
- b)0.15
- c)0.12
- d)0.10
Correct answer is option 'B'. Can you explain this answer?
Two radiating surfaces A1= 6m2 and A2=4m2 have shape factor Then shape factor will be
a)
0.18
b)
0.15
c)
0.12
d)
0.10
|
|
Sarita Yadav answered |
By Reciprocity theorem
A1F12 = A2F21
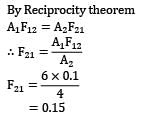
= 0.15
A radiator in a domestic heating system operates at a surface temperature of . Assuming the radiator behaves as a black body, the rate at which it emits the radiant heat per unit area is(Assume σ =5.67 x 10-8 W/m2-k4) - a)0.66 kW/m2
- b)0.0005 kW/m2
- c)0.5kW/m2
- d)66 kW/m2
Correct answer is option 'A'. Can you explain this answer?
A radiator in a domestic heating system operates at a surface temperature of . Assuming the radiator behaves as a black body, the rate at which it emits the radiant heat per unit area is
(Assume σ =5.67 x 10-8 W/m2-k4)
a)
0.66 kW/m2
b)
0.0005 kW/m2
c)
0.5kW/m2
d)
66 kW/m2
|
|
Sarita Yadav answered |
As per Stefan Boltzmann law
Eb = Q/A = σ x T4
Eb = 5.67 x 10-8 x (55 + 273)4
= 656.2 W/m2
≃ 0.66 kW/m2
An industrial furnace employs a hollow brick lining. The inside and outside surfaces of the hollow brick lining are maintained at 900 K and 430 K by placing radiation shields in between the hollow space. The heat loss occurs to the surroundings (300 K) by both radiation and natural convection. Calculate number of shields needed. The emissivity of walls and shields can be taken as 0.85. The convective heat transfer coefficient is governed by the expressionh = 1.5(ΔT)0.33 W/m2- K- a) 11.0
- b) 11.0
Correct answer is option ''. Can you explain this answer?
An industrial furnace employs a hollow brick lining. The inside and outside surfaces of the hollow brick lining are maintained at 900 K and 430 K by placing radiation shields in between the hollow space. The heat loss occurs to the surroundings (300 K) by both radiation and natural convection. Calculate number of shields needed. The emissivity of walls and shields can be taken as 0.85. The convective heat transfer coefficient is governed by the expression
h = 1.5(ΔT)0.33 W/m2- K
a)
11.0
b)
11.0
|
|
Sarita Yadav answered |
Heat lost by outer surface of the lining to surroundings per unit area,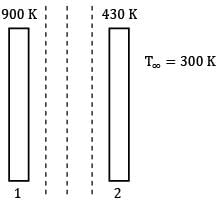
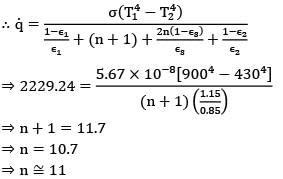
q = εσ(T24 - Tထ4)
q = 0.85 x 5.67 10-8[4304 - 3004]+1.5(430 -300)0.33 x (430 - 300)
q = 1257.3116 + 971.932
q = 2229.24 W

n-shields
∴ Heat transfer from surface 1 to 2 through n-shields must be equal to ̇q
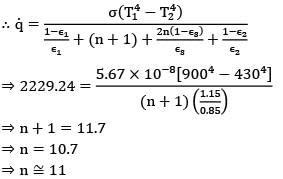
⇒ 2229.24 = 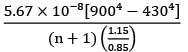
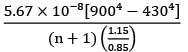
⇒ n+1 = 11.7
⇒ n = 10.7
⇒ n ≅ 11
Question_type 5
On an overcast day the directional distribution of the solar radiation incident on the earth’s surface may be approximated by an expression of the form where In = 80 W/m2is the total intensity of radiation directed normal to the surface and is the zenith angle. What is the solar irradiation at the earth’s surface?- a) 250
- b) 252
Correct answer is between ' 250, 252'. Can you explain this answer?
On an overcast day the directional distribution of the solar radiation incident on the earth’s surface may be approximated by an expression of the form where In = 80 W/m2is the total intensity of radiation directed normal to the surface and is the zenith angle. What is the solar irradiation at the earth’s surface?
a)
250
b)
252
|
|
Sarita Yadav answered |
Consider a point on the earth’s surface receiving solar radiation from all hemispherical directions above the point.
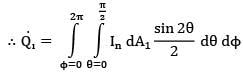
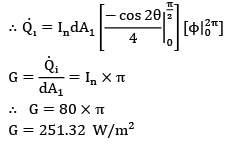

By definition of intensity of radiation
dQ1 = I(dA1 cos ፀ)ωdA2➝dA1 where dA2 is a small area on hemispherical surface.
∴ ωdA2➝dA1 = (rsin ፀ dф)(rdፀ)/r2
= sin ፀ dፀ dф
∴ dQ1 - IdA1 sin θ dθ dф
dQ1 - Incos ө dA1 sin θ dθ dф
dQ1 - IndA1 sin 2θ/2 x dθ dф
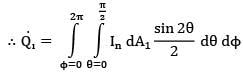
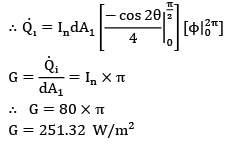
G = Qi/dA1 =In x π
∴ G = 80 x π
G = 251.32 W/m2
What is net radiation heat exchange per square meter per unit time for two very large plates at temperature values of 800 K and 500 K? Emissivities of hot and cold plates are 0.8 and 0.6 respectively. Stefan-Boltzmann constant is - 5.67x10-8W/m2K4- a)1026 kW/m2
- b)10.26 kW/m2
- c)102.6 kW/m2
- d)1.026 kW/m2
Correct answer is option 'B'. Can you explain this answer?
What is net radiation heat exchange per square meter per unit time for two very large plates at temperature values of 800 K and 500 K? Emissivities of hot and cold plates are 0.8 and 0.6 respectively. Stefan-Boltzmann constant is - 5.67x10-8W/m2K4
a)
1026 kW/m2
b)
10.26 kW/m2
c)
102.6 kW/m2
d)
1.026 kW/m2
|
|
Sarita Yadav answered |
For two very large parallel plates, the net radiation heat exchange (using thermal circuit) is given by,
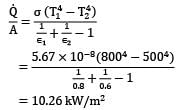
= 10.26 kW/m2
What is the equivalent emissivity for radiant heat exchange between a small body ( in a very large enclosure (emissivity = 0.5)?- a)0.5
- b)0.4
- c)0.2
- d)0.10
Correct answer is option 'B'. Can you explain this answer?
What is the equivalent emissivity for radiant heat exchange between a small body ( in a very large enclosure (emissivity = 0.5)?
a)
0.5
b)
0.4
c)
0.2
d)
0.10

|
Telecom Tuners answered |
If one surface is completely enclosed by another surface,
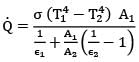
If surface 2 is very large,
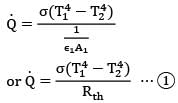
Also we have q = εeσ(T14 - T24) ...②
From ① & ② εe = 1/Rth
But Rth = 1 /ε1A1
∴ εe = ε1 = 0.4
The net radiation heat exchange rate between a heating element at a temperature of 800oC and inner wall of a furnace maintained at . The heat exchange rate when the element temperature is increased to 1000oC for the same furnace temperature is- a)11.2 kW/m2
- b)12.0kW/m2
- c)14.6kW/m2
- d)16.5kW/m2
Correct answer is option 'D'. Can you explain this answer?
The net radiation heat exchange rate between a heating element at a temperature of 800oC and inner wall of a furnace maintained at . The heat exchange rate when the element temperature is increased to 1000oC for the same furnace temperature is
a)
11.2 kW/m2
b)
12.0kW/m2
c)
14.6kW/m2
d)
16.5kW/m2
|
|
Sarita Yadav answered |

By Thermal circuits,
Where R is thermal resistance.
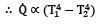
As T2 increases from 800oC to 1000oC, the net heat exchange increases n times
Where
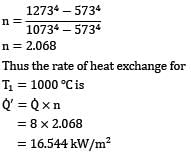
n = 2.068
Thus the rate of heat exchange for
T1 = 10000C
Q’ = Q x n
= 8 x 2.068
= 16.544 kW/m2
Consider sun (radius R) to be a black body of temperature T. Find out the view factor of earth ( with respect to sun. The center to center distance between sun and earth is (l >>r,R).Option~(A) 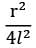 (B)
(B)  (C)
(C) 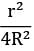 (D)
(D) 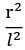 Correct answer is 'A'. Can you explain this answer?
Correct answer is 'A'. Can you explain this answer?
Consider sun (radius R) to be a black body of temperature T. Find out the view factor of earth ( with respect to sun. The center to center distance between sun and earth is (l >>r,R).
Option~
(A) 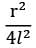
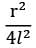
(B) 

(C) 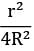
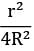
(D) 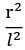
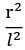
|
|
Sarita Yadav answered |
By definition of view factor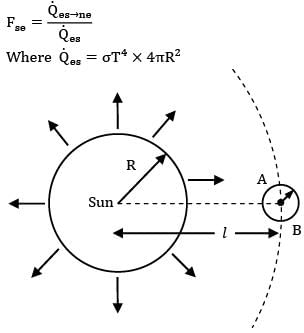

Fse = Qes➝ne/Qes
Where Qes = σT4 x 4πR2
Consider an imaginary sphere of radius l with its center at center of sun. As sun is a symmetric body it emits radiation uniformly in all direction which is received uniformly at surface of imaginary sphere. The energy received by earth is actually the energy to be received by AB portion of the surface of imaginary sphere, where AB is interaction of imaginary sphere and earth. l >> r As therefore AB is nearly a circular surface of area πR2.
Total energy emitted by sum = σ(4πR2)T4
∴ Energy received per unit area of imaginary sphere
= σ(4πR2)T4/4πl2
= σR2T4/l2
∴ Energy received by earth (i.e. surface AB)
= σR2T4/l2 x πr2
Hence Fse = 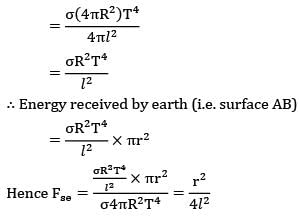
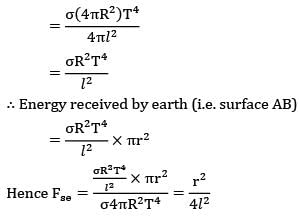
The spectral, hemispherical absorptivity of an opaque surface and the spectral irradiation at the surface are as shown. λ(μm)
λ(μm)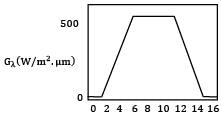 λ(μm)What is the total hemispherical absorptivity of the surface?
λ(μm)What is the total hemispherical absorptivity of the surface?- a) 0.95
- b) 0.97
Correct answer is option ''. Can you explain this answer?
The spectral, hemispherical absorptivity of an opaque surface and the spectral irradiation at the surface are as shown.

λ(μm)

λ(μm)
What is the total hemispherical absorptivity of the surface?
a)
0.95
b)
0.97

|
Telecom Tuners answered |
Based on data given
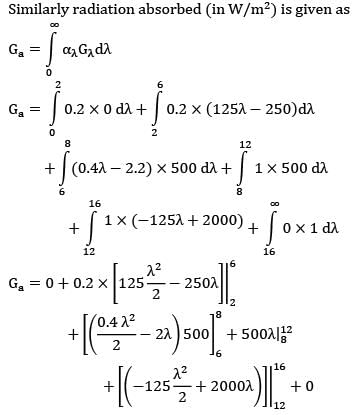
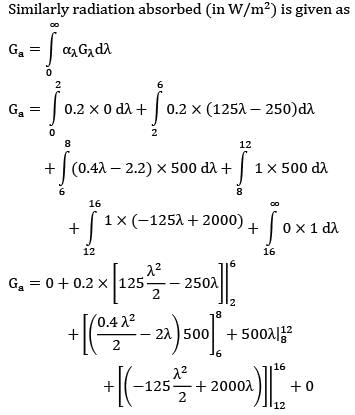

Total irradiation on the surface is
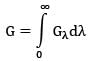
i.e. the area under the curve Gλ vs λ.
G = 0+1/2 x 500 x (6-2) + 500 x (12-6) + 1/2 x 500 x (16-12) + 0
G = 0 + 1000 + 3000 + 1000 + 0
G = 5000 W/m2
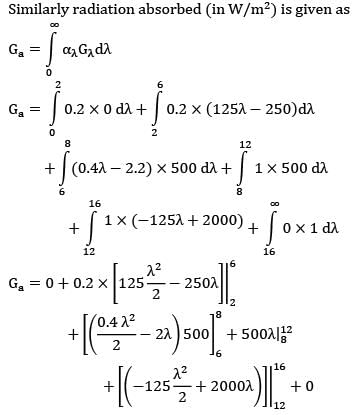
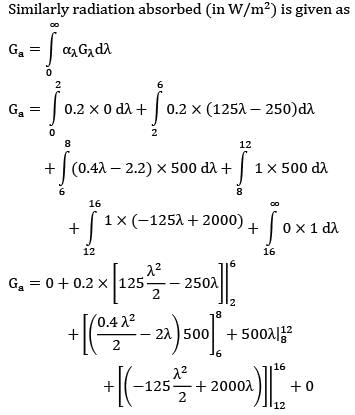
Similarly radiation absorbed (in W/m2 ) is given as
Ga = 1000+800+2000+100
Ga = 4800 W/m2
∴ α = Ga/G
α = 4800/5000
α = 0.96
Quesiton_type: 5
Which of the following statements is false regarding spectral distribution of thermal radiation emitted by a grey surface P. Monochromatic emissivity is independent of wavelength Q. Total emissivity is equal to monochromatic emissivity.R. (monochromatic emissive power) Vs λ( graph for the surface at agiven temperature is scaled down version of the graph for black body at same temperature.S. The wavelength corresponding to maximum monochromatic emissive power is same as that of grey surface at same temperature.- a)Q
- b)R
- c)S
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
Which of the following statements is false regarding spectral distribution of thermal radiation emitted by a grey surface P. Monochromatic emissivity is independent of wavelength Q. Total emissivity is equal to monochromatic emissivity.
R. (monochromatic emissive power) Vs λ( graph for the surface at a
given temperature is scaled down version of the graph for black body at same temperature.
S. The wavelength corresponding to maximum monochromatic emissive power is same as that of grey surface at same temperature.
a)
Q
b)
R
c)
S
d)
None of these
|
|
Sarita Yadav answered |
A grey surface is one for which monochromatic emissivity ελ is independent of wavelength (λ ) But total emissivity (ε) of a surface is given as
ε = E/Eb
Where E & Eb represent total emissive power of the surface and a black surface at same temperature.
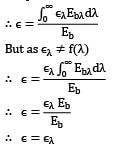
But as ελ ≠ f(λ)
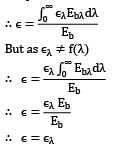
∴ ε = ελEb/Eb
∴ ε = ελ
i.e. total emissivity is equal to monochromatic emissivity. Hence statement Q is also correct.
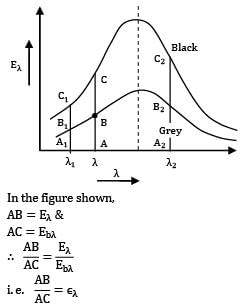
In the figure shown,
AB = Eλ &
AC = Ebλ
∴ AB\Ac = Eλ/Ebλ
i.e, AB\AC = ελ
i.e. ratio of line segment AB and AC is monochromatic emissivity for surface corresponding to wavelength (λ) But as (ελ≠f(λ))
this ratio is same for all λ
i.e, A1B1/A1C1 = AB/AC = A2B2/A2C2
Thus graph of grey surface is simply scaled down version of graph of black surface. This also suggests that corresponding to maxima point for both surfaces is same.
Hence statement R & S are also correct.
Thus all statements are correct & option (D) is the correct answer.
The ratio of total emissive power of body to the total emissive power of a black body at the same temperature is called- a)Absorptivity
- b)Transmissivity
- c)Reflectivity
- d)Emissivity
Correct answer is option 'D'. Can you explain this answer?
The ratio of total emissive power of body to the total emissive power of a black body at the same temperature is called
a)
Absorptivity
b)
Transmissivity
c)
Reflectivity
d)
Emissivity

|
Amar Desai answered |
Emissivity for any body is given by
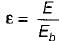
Where
E = Emissive power of a body
Eb = Emissive power of a black body
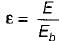
Where
E = Emissive power of a body
Eb = Emissive power of a black body
A small stationary surface of area A1 = 10-4m2 emits diffusely with a total intensity of . A second surface of equivalent area is located at a fixed distance from . The connecting line between the two surfaces remains perpendicular to while rotates at an angular frequency ofፀ2 = dፀ2/dt = 2 rad/s about the axis as shown in the figure.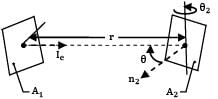 What is the amount of energy intercepted by the two sides of , during one complete revolution?Option~(A) 2 x 10-6j(B) 4 x 10-6j(C) 8.0 x 10-6j(D) 16 x 10-6jCorrect answer is 'C'. Can you explain this answer?
What is the amount of energy intercepted by the two sides of , during one complete revolution?Option~(A) 2 x 10-6j(B) 4 x 10-6j(C) 8.0 x 10-6j(D) 16 x 10-6jCorrect answer is 'C'. Can you explain this answer?
A small stationary surface of area A1 = 10-4m2 emits diffusely with a total intensity of . A second surface of equivalent area is located at a fixed distance from . The connecting line between the two surfaces remains perpendicular to while rotates at an angular frequency of
ፀ2 = dፀ2/dt = 2 rad/s about the axis as shown in the figure.

What is the amount of energy intercepted by the two sides of , during one complete revolution?
Option~
(A) 2 x 10-6j
(B) 4 x 10-6j
(C) 8.0 x 10-6j
(D) 16 x 10-6j
|
|
Sarita Yadav answered |
At time instant t the normal to surface of plate 2 which faces plate 1 makes an angle of ፀ2 with the direction of view ®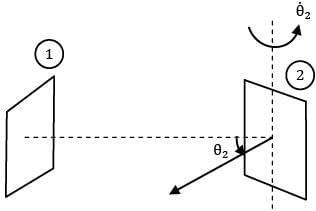
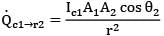
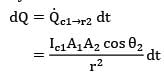
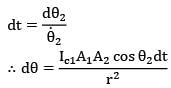

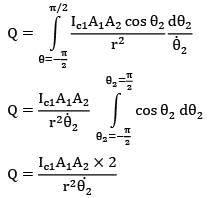

Thus for the given time instant the rate at which energy emitted by 1 strikes at 2 is
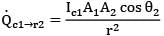
Thus for the given time instant the rate at which energy emitted by 1 strikes at 2 is
dQ = Qc1➝r2 dt
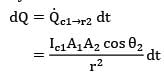
Where,
dt = dፀ2/θ2
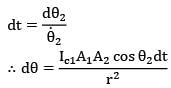
This face of the surface 2 is in front of surface
1 for θ2 = π/2 to π/2
Thus total heat received is

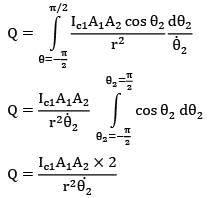
Similarly second face of surface 2 will also come in front of surface 1 during remaining half of revolution Thus total energy received by surface 2 during one complete revolution is
4Ic1A1A2 / r2ፀ2
= 4 x 100 x 10-4 x 10-4/(0.5)2 x 2
= 8 x 10-6 j
Determine the shape factor between a small area and a parallel circular disc A2(diameter D) is located on the axis of the disc and the semi-vertex angle of the cone formed with the disc as base and as the vertex is α.Option~(A) 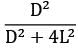 (B)
(B) 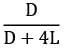 (C)
(C) 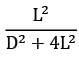 (D)
(D) 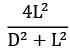 Correct answer is 'A'. Can you explain this answer?
Correct answer is 'A'. Can you explain this answer?
Determine the shape factor between a small area and a parallel circular disc A2(diameter D) is located on the axis of the disc and the semi-vertex angle of the cone formed with the disc as base and as the vertex is α.
Option~
(A) 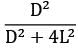
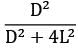
(B) 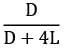
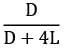
(C) 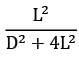
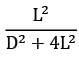
(D) 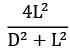
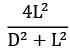

|
Telecom Tuners answered |
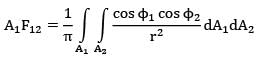
Considering an elementary ring dA2 of width dr at a radius r,
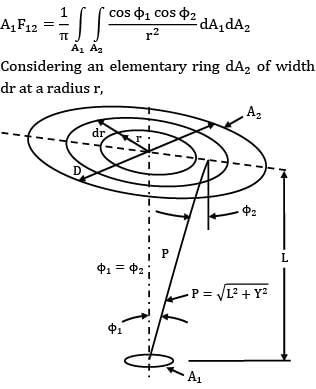
dA2 = 2 πr dr
Now, r = L tanΦ1
Dr = L sec2Ф1dФ1
dA2 = 2πL2 tan Φ1 sec2 Φ1dΦ1
L/P = cos Φ1 or P = L/cosΦ1
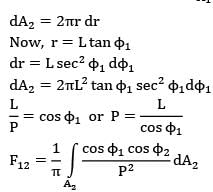
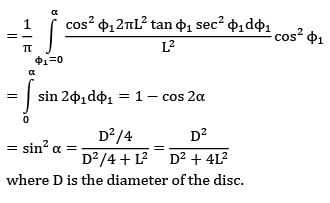
= sin2 α = D2/4/D2/4 + L2 = D2/D2 + 4L2
where D is the diameter of the disc.
Determine the percentage of radiation emitted by the sun within the visible spectrum ( Wavelengths from 0.4 μm (violet) to 0.76 μm(red), considering the sun to be black body and its effective surface temperature to be 5800 K. Given black body radiation function for 2320μmk is 0.124509 and for 4408μmk is 0.550015 .- a)42.5
- b)42.6
- c)42.7
- d)42.8
Correct answer is option 'A'. Can you explain this answer?
Determine the percentage of radiation emitted by the sun within the visible spectrum ( Wavelengths from 0.4 μm (violet) to 0.76 μm(red), considering the sun to be black body and its effective surface temperature to be 5800 K. Given black body radiation function for 2320μmk is 0.124509 and for 4408μmk is 0.550015 .
a)
42.5
b)
42.6
c)
42.7
d)
42.8
|
|
Sarita Yadav answered |
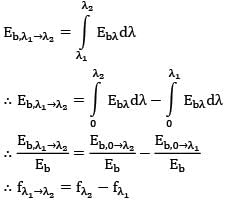
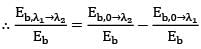
∴ fλ1➝λ2 = fλ2 - fλ1
Where fλ is black body radiation function for wavelength λ.
∴ f0.4-0.76 = f0.76 - f0.4
= 0.550015 - 0.124509
= 0.4255
∴ i.e, ≃ 42.58%
Consider monochromatic emissive power (Eλ) Vs Wavelength(λ) of a black and grey surface both at same temperature. The ratio AB/AC is given as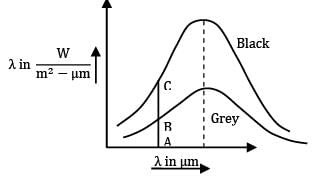
- a)Monochromatic emissivity (λ) of grey surface
- b)Total emissivity (ε) of grey surface
- c)Total emissive power of grey surface
- d)None of the above
Correct answer is option 'A'. Can you explain this answer?
Consider monochromatic emissive power (Eλ) Vs Wavelength(λ) of a black and grey surface both at same temperature. The ratio AB/AC is given as

a)
Monochromatic emissivity (λ) of grey surface
b)
Total emissivity (ε) of grey surface
c)
Total emissive power of grey surface
d)
None of the above
|
|
Sarita Yadav answered |
AB & AC are monochromatic emissive power of grey and black surfaces for same wavelength. Hence, ratio is
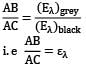
which is monochromatic emissivity of grey surface.
Two infinitely large parallel plates 1 & 2, facing each other are separated by a very small gap. The plates are exchanging heat by thermal radiation and gap between them is filled with non-participating medium. Surface 1 is a black surface with temperature equal to and surface 2 is a grey surface with temperature equal to and emissivity equal to 0.8. Find out the radiosity for surface 2 in kW/m2- a)6.76
- b)6.80
- c)6.81
- d)6.91
Correct answer is option 'A'. Can you explain this answer?
Two infinitely large parallel plates 1 & 2, facing each other are separated by a very small gap. The plates are exchanging heat by thermal radiation and gap between them is filled with non-participating medium. Surface 1 is a black surface with temperature equal to and surface 2 is a grey surface with temperature equal to and emissivity equal to 0.8. Find out the radiosity for surface 2 in kW/m2
a)
6.76
b)
6.80
c)
6.81
d)
6.91
|
|
Sarita Yadav answered |
Consider radiation heat exchange between the surface as shown.
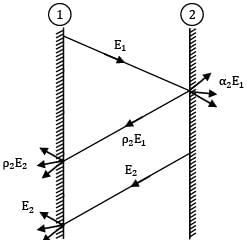
Black Grey,ε2 = 0.8
T1 = 800 K T2 = 500 K
Therefore radiosity for surface 2 is given as
J2 = E2 + ρ2E1
J2 = E2 + (1-α2)E1
By Kirchoff’s law, α2 = ε2
∴ J2 = (1-ε2)E1+ E2
As ① is a black surface,
E1 = σT14
and ② is a gray surface,
E2 = ε2σT24
∴ J2 = (1-ε2)σT14 + ε2σT24
J2 = σ[(1-ε)T14 + ε2T24]
J2 = 5.67 x 10-8 + [(1-0.8) x 8004 + 0.6 x 5004]
J2 = 6.77 kW/m2
For a grey diffuse surface with emissivity ε and temperature T, the intensity of emitted radiation is given as __________. ( is StefanBoltzmann constant.) - a)
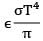
- b)
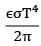
- c)
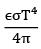
- d)επσT4
Correct answer is option 'A'. Can you explain this answer?
For a grey diffuse surface with emissivity ε and temperature T, the intensity of emitted radiation is given as __________. ( is StefanBoltzmann constant.)
a)
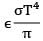
b)
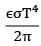
c)
d)
επσT4

|
Telecom Tuners answered |
For a diffuse surface, intensity of emitted radiation (Ie) is same in all directions and is given as
Ie = E/π
Where E is total emissive power
Therefore
Ie = εσT4/π
The spectral hemispherical absorptivity of an opaque surface is as shown.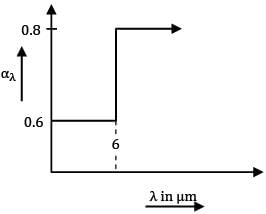 The surface is exposed to ir-radiation for which the spectral distribution is as shown.
The surface is exposed to ir-radiation for which the spectral distribution is as shown.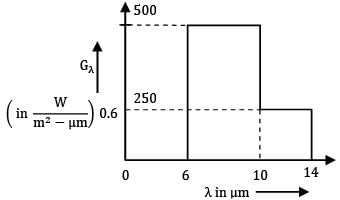 What is the total hemispherical absorptivity of surface?
What is the total hemispherical absorptivity of surface?- a)0.6
- b)0.8
- c)0.7
- d)Data insufficient
Correct answer is option 'B'. Can you explain this answer?
The spectral hemispherical absorptivity of an opaque surface is as shown.

The surface is exposed to ir-radiation for which the spectral distribution is as shown.

What is the total hemispherical absorptivity of surface?
a)
0.6
b)
0.8
c)
0.7
d)
Data insufficient
|
|
Sarita Yadav answered |
Total absorptivity is defined as
α = Ga/G
Where Ga = ∫oooαλGλdλ
Ga = ∫06 0.6 x 0 dλ + ∫610 0.8 x 500 dλ + ∫1014 0.8 x 250 dλ + ∫1400 0.8 x 0 dλ
∴ Ga = 0 + 0.8 x 500 x (10-6) + 0.8 x 250 x (14-10) + 0
Ga = 2400 W/m2 ...①
and
G = ∫000 Gλdλ
I.e. G = Area under graph Gλ Vs λ
G = 500 x (10-6) + 250 x (14-10)
G = 2000 + 1000
G = 3000 W/m2 ...②
Therefore, from ① & ②
α = Ga/G = 2400/3000
α = 0.8
The dark surface of a ceramic stove top may be approximated as a blackbody. The “burners,” which are integral with the stove top, heated from below by electric resistance heaters.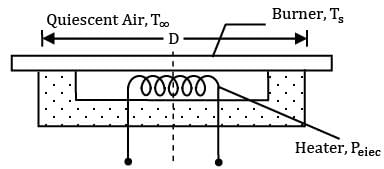 Consider a burner of diameter D = 200mm operating at a uniform surface temperature of Ts = 250oC in ambient air at . Without a pot or pan on the burner, if the efficiency associated with energy transfer from the heaters to the burners is , what is the electric power requirement? (The relation between Nusselt number and Rayleigh number is given as NuL = (RaL)¼)Air (Tf = 408 K)k = 0.0344 x W/mKν = 27.4 x 10-6 m2/sα = 39.7 x 10-6 m2/sPr = 0.70β = 0.00245 K-6
Consider a burner of diameter D = 200mm operating at a uniform surface temperature of Ts = 250oC in ambient air at . Without a pot or pan on the burner, if the efficiency associated with energy transfer from the heaters to the burners is , what is the electric power requirement? (The relation between Nusselt number and Rayleigh number is given as NuL = (RaL)¼)Air (Tf = 408 K)k = 0.0344 x W/mKν = 27.4 x 10-6 m2/sα = 39.7 x 10-6 m2/sPr = 0.70β = 0.00245 K-6- a)202 W
- b)222 W
- c)212 W
- d)232 W
Correct answer is option 'D'. Can you explain this answer?
The dark surface of a ceramic stove top may be approximated as a blackbody. The “burners,” which are integral with the stove top, heated from below by electric resistance heaters.

Consider a burner of diameter D = 200mm operating at a uniform surface temperature of Ts = 250oC in ambient air at . Without a pot or pan on the burner, if the efficiency associated with energy transfer from the heaters to the burners is , what is the electric power requirement? (The relation between Nusselt number and Rayleigh number is given as NuL = (RaL)¼)
Air (Tf = 408 K)
k = 0.0344 x W/mK
ν = 27.4 x 10-6 m2/s
α = 39.7 x 10-6 m2/s
Pr = 0.70
β = 0.00245 K-6
a)
202 W
b)
222 W
c)
212 W
d)
232 W
|
|
Sarita Yadav answered |
For emission from a black body,
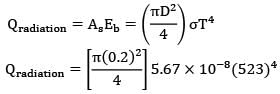
= 13 W
∵ L = As/P = D/4 = 0.2/4 = 0.05 m
⟶ RsL = gβ(Ts-Tꝏ)L3
= 9.81 x 0.00245 x 230 x (0.05)3/27.4 x 39.7 x 10-12
= 6.35 x 105

= 10.5 W/m2 K
∴ Qconv = h As(Ts-Tꝏ)
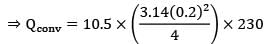
⇒ 75.7 W
∴ Electric power required,

⇒ P = 232 W
A black body of total area 0.045 m2 is completely enclosed in a space bounded by 5 cm thick walls. The walls have a surface area 0.5 m 2 and thermal conductivity 1.07 W/ m K. If the inner surface of the enveloping wall is to be maintained at 215 degree Celsius and the outer wall surface at 30 degree Celsius, calculate the temperature of the black body- a)547.3 K
- b)287.4 K
- c)955.9 K
- d)222.2 K
Correct answer is option 'C'. Can you explain this answer?
A black body of total area 0.045 m2 is completely enclosed in a space bounded by 5 cm thick walls. The walls have a surface area 0.5 m 2 and thermal conductivity 1.07 W/ m K. If the inner surface of the enveloping wall is to be maintained at 215 degree Celsius and the outer wall surface at 30 degree Celsius, calculate the temperature of the black body
a)
547.3 K
b)
287.4 K
c)
955.9 K
d)
222.2 K
|
|
Rajveer Rane answered |
Qr = σ A (T b4 – Tw4), Q c = k A d t/δ = 1979.5 W. So temperature of black body is 955.9 K.
In the previous question if εshield = εsurface, then what will be the number of shields?Option~(A) 100(B) 3(C) 99(D) 4Correct answer is 'C'. Can you explain this answer?
In the previous question if εshield = εsurface, then what will be the number of shields?
Option~
(A) 100
(B) 3
(C) 99
(D) 4
|
|
Sarita Yadav answered |
With introduction of n shields the rate of heat transfer reduces by 99%, therefore,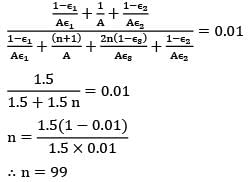
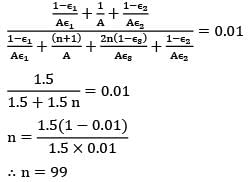
1.5/1.5+1.5n = 0.01
n = 1.5(1-0.01)/1.5 x 0.01
n = 99
This shows that if the emissivity of the surface is large then number of shields should be large as shield shall offer less resistance. Hence for shields to be effective their surface emissivity should be as low as possible.
Determine for the following configuration. Long inclined plates (point B is directly above the center of )
- a)F12 = 0.5, F21 = 0.707
- b)F12 = 0.707, F21 = 0.5
- c)F12 = 0.5, F21 = 0.637
- d)F12 = 0.637, F21 = 0.50
Correct answer is option 'A'. Can you explain this answer?
Determine for the following configuration. Long inclined plates (point B is directly above the center of )

a)
F12 = 0.5, F21 = 0.707
b)
F12 = 0.707, F21 = 0.5
c)
F12 = 0.5, F21 = 0.637
d)
F12 = 0.637, F21 = 0.50
|
|
Sarita Yadav answered |
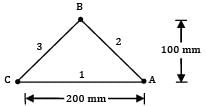
Closing the remaining side by a hypothetical surface 3, we have
F11 + F12 + F13 = 1
F11 = 0; By symmetry we have,
F12 = F13
∴ F12 = F13 = 0.5
A1F12 = A2F21(by reciprocity relation)
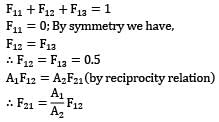
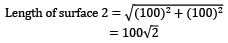

(considering depth of plates ⊥ to plane of paper to be l)
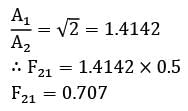
∴ F21 = 1.4142 x 0.5
F21 = 0.707
The spectral distribution of surface irradiation is as follows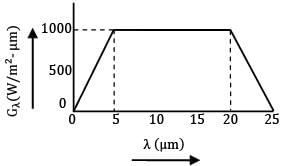 What is the total irradiation in kW/m2 ?
What is the total irradiation in kW/m2 ?- a)10
- b)20
- c)30
- d)40
Correct answer is option 'B'. Can you explain this answer?
The spectral distribution of surface irradiation is as follows

What is the total irradiation in kW/m2 ?
a)
10
b)
20
c)
30
d)
40

|
Telecom Tuners answered |
Total irradiation is given as
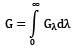
i.e. it is equal to area under the curve Gλ Vs λ Hence,
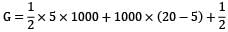
x (25-20) x 1000
∴ G = 20000 W/m2
I.e. G = 20 kW/m2
What will be the view factor for the geometry as shown in the figure (sphere within a hollow cube)?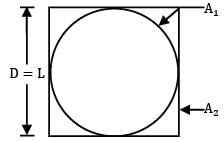
- a)
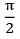
- b)
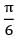
- c)
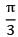
- d)
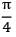
Correct answer is option 'B'. Can you explain this answer?
What will be the view factor for the geometry as shown in the figure (sphere within a hollow cube)?

a)
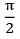
b)
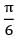
c)
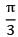
d)
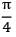
|
|
Sarita Yadav answered |
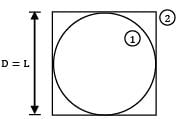
1 is a spherical surface
∴ F11 = 0
By summation rule,
F12 + F11 = 1
∴ F12 = 1
By Reciprocity theorem,
A1F12 = A2F21
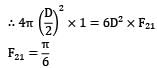
A small surface of area emits radiation as a blackbody at temperature T1 = 600 K. A fraction of energy emitted by A1 strikes another small surface of area A2 = 5 cm2 oriented as shown in the figure A1 = 3 cm2T1 = 600 KFind out view factor of surface with respect to A1 ?Option~(A) 0.6215 x 10-4(B) 1.234 x 10-4(C) 4.14 x 10-4(D) 2.071 x 10-4Correct answer is 'B'. Can you explain this answer?
A1 = 3 cm2T1 = 600 KFind out view factor of surface with respect to A1 ?Option~(A) 0.6215 x 10-4(B) 1.234 x 10-4(C) 4.14 x 10-4(D) 2.071 x 10-4Correct answer is 'B'. Can you explain this answer?
A small surface of area emits radiation as a blackbody at temperature T1 = 600 K. A fraction of energy emitted by A1 strikes another small surface of area A2 = 5 cm2 oriented as shown in the figure

A1 = 3 cm2
T1 = 600 K
Find out view factor of surface with respect to A1 ?
Option~
(A) 0.6215 x 10-4
(B) 1.234 x 10-4
(C) 4.14 x 10-4
(D) 2.071 x 10-4
|
|
Sarita Yadav answered |
View factor (F12 ) is the fraction of energy leaving the surface that is received at surface But as is a black surface, energy leaving the surface is only the emitted radiation.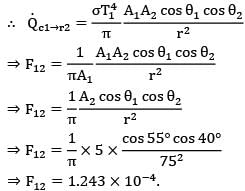
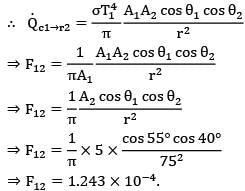
∴ F12 = qc1➝r2/Qc1
By Stefan-Blotzmann law
Qc1 = σA1T14
Also, using the definition of Intensity of emitted radiation,
Qc1➝r2 = Ic1A1 cos ፀ1ω2➝1
Where ω2➝1 is solid angle subtended by point surface 2 over point surface 1.
∴ ω2➝1 = A2cosፀ2/r2
For black surface
Ic1 = σT14/π
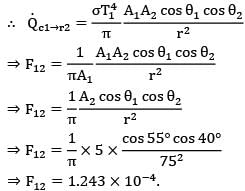
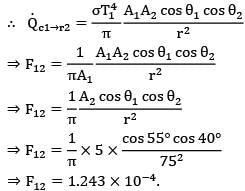
⇒ F12 = 1.243 x 10-4
The spectral emissivity of an opaque surface at 800 K is approximated as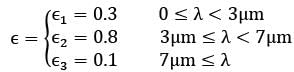
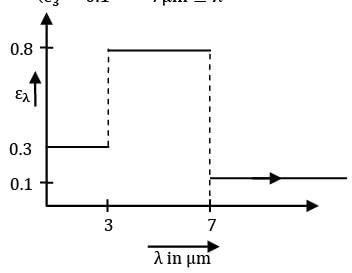 Black body radiation function values for a black surface at 800 K are as follows
Black body radiation function values for a black surface at 800 K are as follows Find the total emissivity of the surface?
Find the total emissivity of the surface?- a)0.4
- b)0.45
- c)0.6
- d)0.52
Correct answer is option 'D'. Can you explain this answer?
The spectral emissivity of an opaque surface at 800 K is approximated as
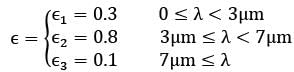

Black body radiation function values for a black surface at 800 K are as follows

Find the total emissivity of the surface?
a)
0.4
b)
0.45
c)
0.6
d)
0.52

|
Telecom Tuners answered |
By definition of total emissivity
ε = E/Eb
Where E = 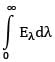
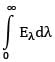
∴ E = 

∴ E = 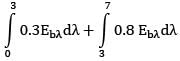
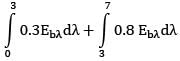
∴ E = 0.3 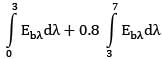
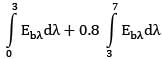
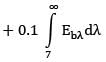
E = 0.3 Eb,0➝3 + 0.8Eb,3➝7 + 0.1Eb,7➝ꝏ
E = 0.3 f3Eb + 0.8f3➝7Eb + 0.1f7➝ꝏEꝏ
E = [0.3f3 + 0.8(f7 -f3) + 0.1(1- f7)]Eb
∴ ε = [0.3f3 + 0.8(f7 - f3 ) + 0.1(1-f7)]
For T = 2400 μm-K
∴ f3 = 0.140256
Similarly for λ = 7 μm
λT = 5600 μm-K
∴ f7 = 0.701046
∴ ε = 0.3 x 0.140256 + 0.8
X (0.701046 - 0.140256) + 0.1 x (1 - 0.701046)
ε = 0.0420768 + 0.448632 + 0.0298954
ε = 0.5206042
≃ 0.52
The shape factor of a cylindrical cavity (open from top) with respect to itself is __________. L & D are length and diameter of the cavity respectively.- a)

- b)
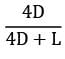
- c)

- d)
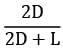
Correct answer is option 'A'. Can you explain this answer?
The shape factor of a cylindrical cavity (open from top) with respect to itself is __________. L & D are length and diameter of the cavity respectively.
a)

b)
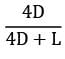
c)

d)
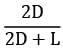

|
Telecom Tuners answered |
The cavity is the shape
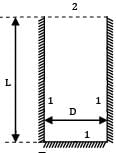
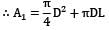
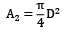
2 is a planar surface
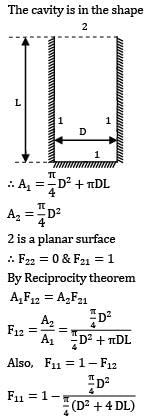
∴ F22 = 0 & F21 = 1
By Reciprocity theorem
A1A12 = A2F21
Also, F11 = 1- F12
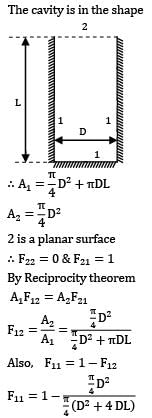
F11 = 1 - D2/D2+4DL
1-D/D+4L
∴ F11 = 4L/D+4L
For the radiation between two infinite parallel planes of emissivity respectively, which one of the following is the expression for emissivity factor or equivalent emissivity?- a)ε1ε2
- b)
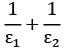
- c)
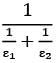
- d)
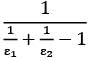
Correct answer is option 'D'. Can you explain this answer?
For the radiation between two infinite parallel planes of emissivity respectively, which one of the following is the expression for emissivity factor or equivalent emissivity?
a)
ε1ε2
b)
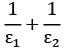
c)
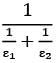
d)
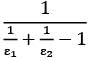

|
Telecom Tuners answered |
The equivalent thermal resistance between two gray bodies is given by
Rth = 1-ε1/A1ε1+1/A1F12+1-ε2/A2ε2
Now for infinite parallel panes, F12 =1
A1 = A2 = A
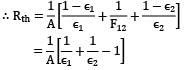
For unit area, A = 1 m2
Rth = 1/ε1+1/ε2-1
Hence equivalent emissivity
Εe = 1/Rth
A small surface of area emits radiation as a blackbody. A fraction of this energy emitted is received by another small area Oriented as shown in figure.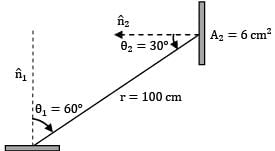 A1 = 2 cm2The rate at which radiation emitted by surface 1 strikes is measured to be 274 x 10-6 W. Determine the surface temperature of in K?
A1 = 2 cm2The rate at which radiation emitted by surface 1 strikes is measured to be 274 x 10-6 W. Determine the surface temperature of in K?- a) 550
- b) 555
Correct answer is between ' 550, 555'. Can you explain this answer?
A small surface of area emits radiation as a blackbody. A fraction of this energy emitted is received by another small area Oriented as shown in figure.

A1 = 2 cm2
The rate at which radiation emitted by surface 1 strikes is measured to be 274 x 10-6 W. Determine the surface temperature of in K?
a)
550
b)
555
|
|
Sarita Yadav answered |
As surface 1 is a black surface, the energy leaving the surface is only the energy emitted by the surface.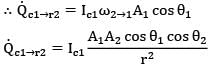

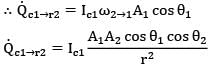
Also by definition of black surface (diffuse characteristics)
Ic1 = σT14/π

274 x 10-6 W = 5.67 x 10-1 W/m2- K4 x T14 x ( 2cm2 x 6 cm2) x cos 60o x cos 30o /(100 cm)2
274 x 10-6 = 5.67 x 10-8 x 12 x 10-4/ 104 x 1/2 x ✓3/4 x T14
274 x 10-6 x 10-8 x 4 / 5.67 x 12 x ✓3 = T14
∴ T14 = 9.30 x 1010
T1 = 552.23 K
What is the view factor for inclined parallel plates of equal width and a common edge? The width of plates to the plane of paper is b. (b >>L)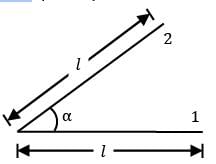
- a)1 + sin α
- b)1 - sin(α/2)
- c)1 - sin α
- d)1+ sin(α/2)
Correct answer is option 'B'. Can you explain this answer?
What is the view factor for inclined parallel plates of equal width and a common edge? The width of plates to the plane of paper is b. (b >>L)

a)
1 + sin α
b)
1 - sin(α/2)
c)
1 - sin α
d)
1+ sin(α/2)

|
Telecom Tuners answered |
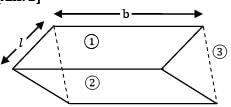
Let us imagine the rectangular gap as a surface ③. !s the energy going out of triangular gaps can be neglected, but for rectangular gap, it is quite significant
Length of side 3 = 2 ℓ sin(α/2)
∴ A3 = (2 ℓ sin α/2 x b) = 2 ℓb sin (α/2)
A1 = ℓ x b = ℓb
A2 = ℓ x b = ℓlb
As 3 is a planar surface
F33 = 0
Also F31 + F32 + F33 =1
But because of symmetric arrangement of ①
& ② with respect to ③
F31 = F32
∴ F31 = F32 = 0.5
By Reciprocity theorem
A1A13 = A3A31
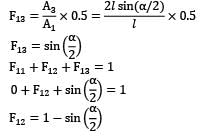
F13 = ain(α/2)
F11 + F12 + F13 = 1
0 + F12 + sin (α/2) = 1
F12 = 1-sin(α/2)
A metal storage tank with planar surfaces of external area contains water at and is located inside a large enclosure with walls at 65oC . The tank is initially painted black on the outside and its emissivity is approximated to 0.95. How much percentage reduction in heat loss would occur if the outside surface of tank is coated with aluminium paint (instead of black) of emissivity 0.55? Take radiation constantσb = 5.67 x 10-8 W/m2K4- a)58
- b)42
- c)29
- d)21
Correct answer is option 'A'. Can you explain this answer?
A metal storage tank with planar surfaces of external area contains water at and is located inside a large enclosure with walls at 65oC . The tank is initially painted black on the outside and its emissivity is approximated to 0.95. How much percentage reduction in heat loss would occur if the outside surface of tank is coated with aluminium paint (instead of black) of emissivity 0.55? Take radiation constant
σb = 5.67 x 10-8 W/m2K4
a)
58
b)
42
c)
29
d)
21
|
|
Sarita Yadav answered |
Consider outer surface of metal tank to be 1 & inner surface of enclosure to be surface 2.
By concept of thermal circuits
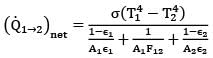
As the surfaces of 1 are planar, F11 = 0
∴ F21 = 1
Also ,
A2 >> A1
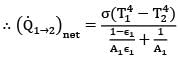
∴ (Q1➝2)net = σA1ε1(T14 - T24)
∴ Q ∝ ε1
Q0.55/Q0.95 = 0.55/0.95 = 0.4211
Thus heat exchange rate decreases by 57.89 %, by painting the tank with aluminium paint.
A cake is being baked in an hemispherical oven of radius 500 mm. The lower surface of the oven is maintained at 1000 K while the covering surface ( is maintained at 800 K. The diameter of the round cake is 0.25 m and its height can be neglected. Considering the lower surface of the oven and cake to be black bodies and neglecting the area covered by the cake, find the time required to bake the cake, if it requires 3.2123 MJ.- a) 44.0
- b) 46.0
Correct answer is between ' 44.0, 46.0'. Can you explain this answer?
A cake is being baked in an hemispherical oven of radius 500 mm. The lower surface of the oven is maintained at 1000 K while the covering surface ( is maintained at 800 K. The diameter of the round cake is 0.25 m and its height can be neglected. Considering the lower surface of the oven and cake to be black bodies and neglecting the area covered by the cake, find the time required to bake the cake, if it requires 3.2123 MJ.
a)
44.0
b)
46.0
|
|
Sarita Yadav answered |
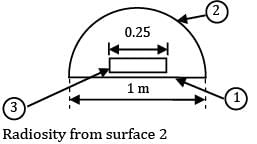 ’
’Radiosity from surface 2
= reflected energy from ② + emitted energy from ②
⇒ J2 = ρ2σA1T14 + ε2 A2 σT24
Ε2 = 0.8 ⇒ α2 = 0.8
∴ α2+ρ2+τ2 = 1
⇒ ρ2 = 0.2

⇒ J2 = 38,071.644 W
Energy incident on the cake, G3 = F23J2
A3F32 = A2F23
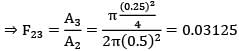
∴ G3 = 0.03125 x 38071.644
G3 = 1189.74 W
∴ Time required to bake the cake,
t = 3.2123 x 106/1189.74
⇒ t = 2700 s
⇒ t ≅ 45 min
Consider a deep-space probe constructed as 1 m diameter polished aluminum sphere. Estimate the equilibrium temperature that the probe reaches if the solar energy received is 300 W/m2. For solar radiation, absorptivity of aluminum is 0.3 and the average emissivity appropriate for aluminum at low temperature is 0.04- a)415.67 K
- b)315.67 K
- c)215.67 K
- d)115.67 K
Correct answer is option 'B'. Can you explain this answer?
Consider a deep-space probe constructed as 1 m diameter polished aluminum sphere. Estimate the equilibrium temperature that the probe reaches if the solar energy received is 300 W/m2. For solar radiation, absorptivity of aluminum is 0.3 and the average emissivity appropriate for aluminum at low temperature is 0.04
a)
415.67 K
b)
315.67 K
c)
215.67 K
d)
115.67 K

|
Shivam Sharma answered |
Q in = α q A P = 70.7 W. Q out = E σ b A T ^4. Correct option is (b).
For the same type of shapes, the value of radiation shape factor will be higher when- a)Surfaces are closer
- b)Surfaces are larger and held closer
- c)Surfaces are moved further apart
- d)Surfaces are smaller and held closer
Correct answer is option 'B'. Can you explain this answer?
For the same type of shapes, the value of radiation shape factor will be higher when
a)
Surfaces are closer
b)
Surfaces are larger and held closer
c)
Surfaces are moved further apart
d)
Surfaces are smaller and held closer
|
|
Aarav Mehta answered |
Obviously the value of radiation shape factor will be higher when surfaces are larger and held closer.
A perfectly black body- a)Absorbs all the incident radiation
- b)Allow all the incident radiation to pass through it
- c)Reflects all the incident radiation
- d)Has its surface coated with lamp black or graphite
Correct answer is option 'A'. Can you explain this answer?
A perfectly black body
a)
Absorbs all the incident radiation
b)
Allow all the incident radiation to pass through it
c)
Reflects all the incident radiation
d)
Has its surface coated with lamp black or graphite
|
|
Bhaskar Banerjee answered |
A black body is a perfect emitter and absorber.
The temperature of the photosphere, referred to as the effective temperature of the sun, is usually taken as- a)3000 K
- b)4000 K
- c)5000 K
- d)6000 K
Correct answer is option 'D'. Can you explain this answer?
The temperature of the photosphere, referred to as the effective temperature of the sun, is usually taken as
a)
3000 K
b)
4000 K
c)
5000 K
d)
6000 K
|
|
Tushar Verma answered |
The sun consists of a central hot portion surrounded by the photosphere.
Of the radiant energy 350W/m2 incident upon a surface 250W/m2 is absorbed, 60W/m2 is reflected and the remainder is transmitted through the surface. Workout the value for absorptivity for the surface material- a)0.123
- b)0.714
- c)0.684
- d)0.386
Correct answer is option 'B'. Can you explain this answer?
Of the radiant energy 350W/m2 incident upon a surface 250W/m2 is absorbed, 60W/m2 is reflected and the remainder is transmitted through the surface. Workout the value for absorptivity for the surface material
a)
0.123
b)
0.714
c)
0.684
d)
0.386
|
|
Manoj Kumar answered |
Absorptivity = 250/350 = 0.714.
Consider an infinitely long three sided triangular enclosure with sides 2 cm, 3 cm and 4 cm. The view factor from 2 cm side to 4 cm side is __________.- a) 0.58
- b) 0.59
Correct answer is option ''. Can you explain this answer?
Consider an infinitely long three sided triangular enclosure with sides 2 cm, 3 cm and 4 cm. The view factor from 2 cm side to 4 cm side is __________.
a)
0.58
b)
0.59
|
|
Sarita Yadav answered |
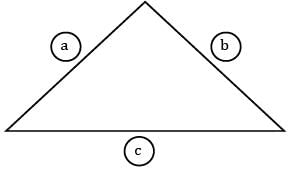
Given la = 2 cm
Lb = 3 cm
Lc = 4 cm
By energyF conservation principle
Faa + Fab + Fac = 1
Fba + Fbb + Fbc = 1
Fca + Fcb + Fcc = 1
As a,b,c are planar surfaces
Faa, Fbb, Fcc, = 0
Therefore the equations are reduced to
Fab + Fac = 1 ….①
Fba + Fbc + = 1 ...②
Fca + Fcb = 1 ….③
By Reciprocity theorem
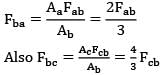
Substituting Fba & Fbc in equation ②
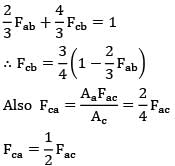
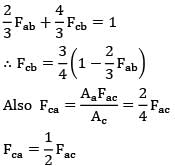
Substituting Fcb & Fca in equation ③
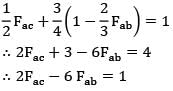
∴ 2Fac - 6Fab = 1
Fac - 3Fab = 1/2 ….Ⓢ
Solving equation ① & Ⓢ together
Fab + Fac =1
Fac - 3Fab = 1/2
____________
3Fab + 3ac = 3
3Fac - 3Fab = 1/2
+ + +
______________
6Fac = 7/2
Fac = 7/12
Fac 0.5833
Question_type 5
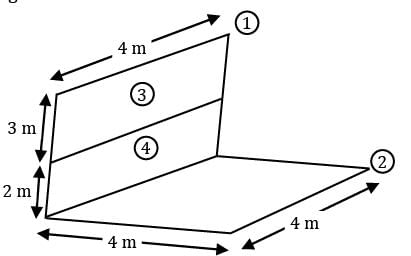
An enclosure consists of four surfaces 1, 2, 3 and 4. The view factors for radiation heat transfers are
F 11 = 0.1
F 12 = 0.4
F 13 = 0.25
The surface areas A 1 and A 2 are 4 m2 and 2 m2. The view factor F 41 is- a)0.50
- b)0.75
- c)0.1
- d)0.25
Correct answer is option 'A'. Can you explain this answer?
An enclosure consists of four surfaces 1, 2, 3 and 4. The view factors for radiation heat transfers are
F 11 = 0.1
F 12 = 0.4
F 13 = 0.25
The surface areas A 1 and A 2 are 4 m2 and 2 m2. The view factor F 41 is
F 11 = 0.1
F 12 = 0.4
F 13 = 0.25
The surface areas A 1 and A 2 are 4 m2 and 2 m2. The view factor F 41 is
a)
0.50
b)
0.75
c)
0.1
d)
0.25
|
|
Nilotpal Sharma answered |
F 11 + F 12 + F 13 + F 14 = 1.
Chapter doubts & questions for Radiation - Heat Transfer 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Radiation - Heat Transfer in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Heat Transfer
59 videos|108 docs|86 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup