All Exams >
Bank Exams >
Quantitative Aptitude for Competitive Examinations >
All Questions
All questions of Pipes and Cistern for Bank Exams Exam
A funnel can discharge a tank in 40 minutes. A second pipe with distance across twice as much as that of the first is likewise joined with the tank to purge it. The two together can exhaust the tank in:- a)8 min
- b)40/3 min
- c)30 min
- d)38 min
Correct answer is option 'B'. Can you explain this answer?
A funnel can discharge a tank in 40 minutes. A second pipe with distance across twice as much as that of the first is likewise joined with the tank to purge it. The two together can exhaust the tank in:
a)
8 min
b)
40/3 min
c)
30 min
d)
38 min
|
Nilesh Banerjee answered |
Understanding the Problem
To determine how long it takes for two pipes to discharge a tank together, we start with the information given:
- A funnel discharges the tank in 40 minutes.
- A second pipe has a distance across twice as much as the first.
Calculating Individual Rates
- The rate of the first pipe (funnel) is:
Rate1 = 1 tank / 40 min = 1/40 tanks per minute.
- The second pipe is not explicitly given a discharge time, but since it’s twice the distance, we can assume it discharges at half the rate of the first pipe.
Rate2 = 1/80 tanks per minute (since it takes twice as long due to the greater distance).
Combined Rate of Both Pipes
To find out how quickly both pipes can discharge the tank together, we add their rates:
- Combined Rate = Rate1 + Rate2
Combined Rate = (1/40 + 1/80) tanks per minute.
To add these fractions, we find a common denominator (which is 80):
- Combined Rate = (2/80 + 1/80) = 3/80 tanks per minute.
Time Taken to Discharge the Tank
Now, to find the time taken to discharge 1 tank using the combined rate:
- Time = 1 tank / (3/80 tanks per minute)
- Time = 80/3 minutes.
Thus, the two pipes together can exhaust the tank in 80/3 minutes, which is approximately 26.67 minutes.
Conclusion
The correct answer is option 'B': 40/3 minutes. This matches our calculated result, confirming that the combined effort of both pipes significantly reduces the time taken to discharge the tank.
To determine how long it takes for two pipes to discharge a tank together, we start with the information given:
- A funnel discharges the tank in 40 minutes.
- A second pipe has a distance across twice as much as the first.
Calculating Individual Rates
- The rate of the first pipe (funnel) is:
Rate1 = 1 tank / 40 min = 1/40 tanks per minute.
- The second pipe is not explicitly given a discharge time, but since it’s twice the distance, we can assume it discharges at half the rate of the first pipe.
Rate2 = 1/80 tanks per minute (since it takes twice as long due to the greater distance).
Combined Rate of Both Pipes
To find out how quickly both pipes can discharge the tank together, we add their rates:
- Combined Rate = Rate1 + Rate2
Combined Rate = (1/40 + 1/80) tanks per minute.
To add these fractions, we find a common denominator (which is 80):
- Combined Rate = (2/80 + 1/80) = 3/80 tanks per minute.
Time Taken to Discharge the Tank
Now, to find the time taken to discharge 1 tank using the combined rate:
- Time = 1 tank / (3/80 tanks per minute)
- Time = 80/3 minutes.
Thus, the two pipes together can exhaust the tank in 80/3 minutes, which is approximately 26.67 minutes.
Conclusion
The correct answer is option 'B': 40/3 minutes. This matches our calculated result, confirming that the combined effort of both pipes significantly reduces the time taken to discharge the tank.
A cistern is provided with two pipes A and B. A can fill it in 20 minutes and B can empty it in 30 minutes. If A and B be kept open alternately for one minute each, how soon will the cistern be filled ?- a)120 minutes
- b)121 minutes
- c)110 minutes
- d)115 minutes
Correct answer is option 'D'. Can you explain this answer?
A cistern is provided with two pipes A and B. A can fill it in 20 minutes and B can empty it in 30 minutes. If A and B be kept open alternately for one minute each, how soon will the cistern be filled ?
a)
120 minutes
b)
121 minutes
c)
110 minutes
d)
115 minutes
|
EduRev SSC CGL answered |
Using Rule 7,
Part of the tank filled in first two minutes
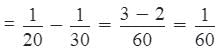
Part of tank filled in 114 minutes
= 57/60 = 19/20
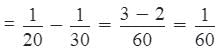
Part of tank filled in 114 minutes
= 57/60 = 19/20
A tank can be filled by pipe A in 2 hours and pipe B in 6 hours. At 10 A.M. pipe A was opened. At what time will the tank be filled if pipe B is opened at 11 A.M.?- a)12 P.M.
- b)12.45 A.M.
- c)5 P.M
- d)11.45 A.M.
Correct answer is option 'D'. Can you explain this answer?
A tank can be filled by pipe A in 2 hours and pipe B in 6 hours. At 10 A.M. pipe A was opened. At what time will the tank be filled if pipe B is opened at 11 A.M.?
a)
12 P.M.
b)
12.45 A.M.
c)
5 P.M
d)
11.45 A.M.
|
Target Study Academy answered |
Part of the tank filled in 1 hour by pipe A = 1/2
Part of the tank filled by both pipes in1 hour
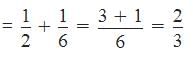
So, Time taken to fill 2/3 part = 60 minutes
Time taken to fill 1/2 part
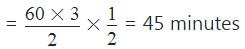
The tank will be filled at 11:45 A.M.
Part of the tank filled by both pipes in1 hour
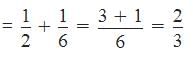
So, Time taken to fill 2/3 part = 60 minutes
Time taken to fill 1/2 part
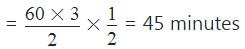
The tank will be filled at 11:45 A.M.
If two pipes function simultaneously, a tank is filled in 12 hours. One pipe fills the tank 10 hours faster than the other. How many hours does the faster pipe alone take to fill the tank?- a)12 hrs
- b)20 hrs
- c)18 hrs
- d)15 hrs
Correct answer is option 'B'. Can you explain this answer?
If two pipes function simultaneously, a tank is filled in 12 hours. One pipe fills the tank 10 hours faster than the other. How many hours does the faster pipe alone take to fill the tank?
a)
12 hrs
b)
20 hrs
c)
18 hrs
d)
15 hrs
|
Malavika Rane answered |
Understanding the Problem
To tackle the problem, let's define the variables and the relationships between the pipes.
- Let the time taken by the slower pipe to fill the tank be \( x \) hours.
- Then, the faster pipe will take \( x - 10 \) hours to fill the tank.
Working Together
When both pipes work together, they fill the tank in 12 hours. The rates of filling for each pipe are:
- Slower pipe: \( \frac{1}{x} \) (tank per hour)
- Faster pipe: \( \frac{1}{x - 10} \) (tank per hour)
The combined rate of both pipes working together is:
\[ \frac{1}{x} + \frac{1}{x - 10} = \frac{1}{12} \]
Setting Up the Equation
To find \( x \), we can combine the fractions:
\[ \frac{(x - 10) + x}{x(x - 10)} = \frac{1}{12} \]
This simplifies to:
\[ \frac{2x - 10}{x^2 - 10x} = \frac{1}{12} \]
Cross-multiplying gives:
\[ 12(2x - 10) = x^2 - 10x \]
Expanding and rearranging results in:
\[ x^2 - 34x + 120 = 0 \]
Solving the Quadratic Equation
Now, we can solve this quadratic equation using the quadratic formula:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Where \( a = 1, b = -34, c = 120 \):
- Discriminant: \( b^2 - 4ac = 1156 - 480 = 676 \)
- Roots:
\[ x = \frac{34 \pm 26}{2} \]
Calculating gives:
- \( x = 30 \) (slower pipe)
- \( x = 4 \) (not valid since it must be greater than 10)
Therefore, the slower pipe takes 30 hours, and the faster pipe takes:
\[ x - 10 = 30 - 10 = 20 \text{ hours} \]
Conclusion
The faster pipe alone takes 20 hours to fill the tank, confirming the correct answer is option B.
To tackle the problem, let's define the variables and the relationships between the pipes.
- Let the time taken by the slower pipe to fill the tank be \( x \) hours.
- Then, the faster pipe will take \( x - 10 \) hours to fill the tank.
Working Together
When both pipes work together, they fill the tank in 12 hours. The rates of filling for each pipe are:
- Slower pipe: \( \frac{1}{x} \) (tank per hour)
- Faster pipe: \( \frac{1}{x - 10} \) (tank per hour)
The combined rate of both pipes working together is:
\[ \frac{1}{x} + \frac{1}{x - 10} = \frac{1}{12} \]
Setting Up the Equation
To find \( x \), we can combine the fractions:
\[ \frac{(x - 10) + x}{x(x - 10)} = \frac{1}{12} \]
This simplifies to:
\[ \frac{2x - 10}{x^2 - 10x} = \frac{1}{12} \]
Cross-multiplying gives:
\[ 12(2x - 10) = x^2 - 10x \]
Expanding and rearranging results in:
\[ x^2 - 34x + 120 = 0 \]
Solving the Quadratic Equation
Now, we can solve this quadratic equation using the quadratic formula:
\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]
Where \( a = 1, b = -34, c = 120 \):
- Discriminant: \( b^2 - 4ac = 1156 - 480 = 676 \)
- Roots:
\[ x = \frac{34 \pm 26}{2} \]
Calculating gives:
- \( x = 30 \) (slower pipe)
- \( x = 4 \) (not valid since it must be greater than 10)
Therefore, the slower pipe takes 30 hours, and the faster pipe takes:
\[ x - 10 = 30 - 10 = 20 \text{ hours} \]
Conclusion
The faster pipe alone takes 20 hours to fill the tank, confirming the correct answer is option B.
Taps A, B and C are connected to a water tank and the rate of flow of water is 42 ltr/hr, 56 ltr/hr and 48 ltr/hr respectively. A and ill fill the tank while tap C empties the tank. If the three taps are opened simultaneously, the tank gets filled up completely in 16 hours. What is the capacity of the tank?- a)800 ltr
- b)960 ltr
- c)2346 ltr
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Taps A, B and C are connected to a water tank and the rate of flow of water is 42 ltr/hr, 56 ltr/hr and 48 ltr/hr respectively. A and ill fill the tank while tap C empties the tank. If the three taps are opened simultaneously, the tank gets filled up completely in 16 hours. What is the capacity of the tank?
a)
800 ltr
b)
960 ltr
c)
2346 ltr
d)
None of these
|
|
EduRev SSC CGL answered |
Net amount of water filled in 1 hr when all the pipes are opened simultaneously = 42 + 56 ? 48 = 50 ltr
Tank gets completely filled in 16 hrs.
∴ Capacity of tank = 16*50 = 800 liters.
Tank gets completely filled in 16 hrs.
∴ Capacity of tank = 16*50 = 800 liters.
Two channels can fill a tank in 15 hours and 12 hours separately and a third pipe can purge it in 4 hours. In the event that the channels are opened all together at 8 am, 9 am and 11am separately, the tank will be exhausted at- a)11.40 am
- b)12.40 pm
- c)1.40 pm
- d)2.40 pm
Correct answer is option 'D'. Can you explain this answer?
Two channels can fill a tank in 15 hours and 12 hours separately and a third pipe can purge it in 4 hours. In the event that the channels are opened all together at 8 am, 9 am and 11am separately, the tank will be exhausted at
a)
11.40 am
b)
12.40 pm
c)
1.40 pm
d)
2.40 pm
|
Arnav Saini answered |
Given Data:
- First channel fills the tank in 15 hours
- Second channel fills the tank in 12 hours
- Third pipe empties the tank in 4 hours
Approach:
- Find the filling rate per hour for each channel
- Calculate the net filling rate when all channels are opened simultaneously
- Determine the time taken to empty the tank
Calculations:
- Filling rate for first channel = 1/15 tank/hour
- Filling rate for second channel = 1/12 tank/hour
- Emptying rate for third pipe = 1/4 tank/hour
- Combined filling rate = 1/15 + 1/12 - 1/4 = 1/20 tank/hour
- Time taken to empty the tank with the combined rate = 1 / (1/20) = 20 hours
- Channels opened at 8 am, 9 am, and 11 am respectively
- Tank will be emptied at 8 am + 20 hours = 4 pm
Final Answer:
- The tank will be emptied at 4.00 pm (Option D)
- First channel fills the tank in 15 hours
- Second channel fills the tank in 12 hours
- Third pipe empties the tank in 4 hours
Approach:
- Find the filling rate per hour for each channel
- Calculate the net filling rate when all channels are opened simultaneously
- Determine the time taken to empty the tank
Calculations:
- Filling rate for first channel = 1/15 tank/hour
- Filling rate for second channel = 1/12 tank/hour
- Emptying rate for third pipe = 1/4 tank/hour
- Combined filling rate = 1/15 + 1/12 - 1/4 = 1/20 tank/hour
- Time taken to empty the tank with the combined rate = 1 / (1/20) = 20 hours
- Channels opened at 8 am, 9 am, and 11 am respectively
- Tank will be emptied at 8 am + 20 hours = 4 pm
Final Answer:
- The tank will be emptied at 4.00 pm (Option D)
Three taps A,B and C together can fill an empty cistern in 10 minutes. The tap A alone can fill it in 30 minutes and the tap B alone in 40 minutes. How long will the tap C alone take to fill it ?- a)40 minutes
- b)16 minutes
- c)24 minutes
- d)32 minutes
Correct answer is option 'C'. Can you explain this answer?
Three taps A,B and C together can fill an empty cistern in 10 minutes. The tap A alone can fill it in 30 minutes and the tap B alone in 40 minutes. How long will the tap C alone take to fill it ?
a)
40 minutes
b)
16 minutes
c)
24 minutes
d)
32 minutes
|
Ishaan Roy answered |
Understanding the Problem
We have three taps A, B, and C which can fill a cistern in different times. We need to find out how long tap C takes to fill the cistern alone.
Given Information
- All taps together (A, B, C) can fill the cistern in 10 minutes.
- Tap A alone can fill the cistern in 30 minutes.
- Tap B alone can fill the cistern in 40 minutes.
Filling Rates Calculation
- Rate of Tap A:
A fills 1/30 of the cistern per minute.
- Rate of Tap B:
B fills 1/40 of the cistern per minute.
- Rate of Tap C:
Let the rate of tap C be 1/x of the cistern per minute.
- Combined Rate:
Together, A, B, and C fill 1/10 of the cistern per minute.
Setting Up the Equation
We can set up the equation based on their combined rates:
(1/30) + (1/40) + (1/x) = 1/10
Finding a Common Denominator
- The least common multiple of 30, 40, and 10 is 120.
- Convert each rate to have a denominator of 120:
- (1/30) = 4/120
- (1/40) = 3/120
- (1/10) = 12/120
Now we can rewrite the equation:
4/120 + 3/120 + 1/x = 12/120
Solving for Tap C's Rate
- Combine the fractions:
(4 + 3)/120 + 1/x = 12/120
7/120 + 1/x = 12/120
- Rearranging gives us:
1/x = 12/120 - 7/120
1/x = 5/120
- Therefore, x = 24 minutes.
Conclusion
Thus, tap C alone will take 24 minutes to fill the cistern. The correct answer is option 'C'.
We have three taps A, B, and C which can fill a cistern in different times. We need to find out how long tap C takes to fill the cistern alone.
Given Information
- All taps together (A, B, C) can fill the cistern in 10 minutes.
- Tap A alone can fill the cistern in 30 minutes.
- Tap B alone can fill the cistern in 40 minutes.
Filling Rates Calculation
- Rate of Tap A:
A fills 1/30 of the cistern per minute.
- Rate of Tap B:
B fills 1/40 of the cistern per minute.
- Rate of Tap C:
Let the rate of tap C be 1/x of the cistern per minute.
- Combined Rate:
Together, A, B, and C fill 1/10 of the cistern per minute.
Setting Up the Equation
We can set up the equation based on their combined rates:
(1/30) + (1/40) + (1/x) = 1/10
Finding a Common Denominator
- The least common multiple of 30, 40, and 10 is 120.
- Convert each rate to have a denominator of 120:
- (1/30) = 4/120
- (1/40) = 3/120
- (1/10) = 12/120
Now we can rewrite the equation:
4/120 + 3/120 + 1/x = 12/120
Solving for Tap C's Rate
- Combine the fractions:
(4 + 3)/120 + 1/x = 12/120
7/120 + 1/x = 12/120
- Rearranging gives us:
1/x = 12/120 - 7/120
1/x = 5/120
- Therefore, x = 24 minutes.
Conclusion
Thus, tap C alone will take 24 minutes to fill the cistern. The correct answer is option 'C'.
Three taps A, B, C can fill an overhead tank in 4, 6 and 12 hours respectively. How long would the three taps take to fill the tank if all of them are opened together ?- a)5 hrs.
- b)2 hrs.
- c)4 hrs.
- d)3 hrs.
Correct answer is option 'B'. Can you explain this answer?
Three taps A, B, C can fill an overhead tank in 4, 6 and 12 hours respectively. How long would the three taps take to fill the tank if all of them are opened together ?
a)
5 hrs.
b)
2 hrs.
c)
4 hrs.
d)
3 hrs.
|
Pioneer Academy answered |
Using Rule 2,
Part of the tank filled by all three taps in an hour
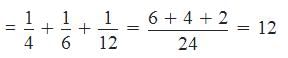
Hence, the tank will be filled in 2 hours.
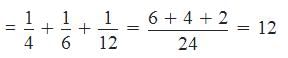
Hence, the tank will be filled in 2 hours.
A break in the base of a tank can purge the full tank in 6 hours. A channel funnel fills water at the rate of 4 liters for each moment. At the point when the tank is full, the channel is opened and because of the break, the tank is void in 8 hours. The limit of the tank is- a)5260 ltr.
- b)5760 ltr.
- c)5846 ltr.
- d)6970 ltr.
Correct answer is option 'B'. Can you explain this answer?
A break in the base of a tank can purge the full tank in 6 hours. A channel funnel fills water at the rate of 4 liters for each moment. At the point when the tank is full, the channel is opened and because of the break, the tank is void in 8 hours. The limit of the tank is
a)
5260 ltr.
b)
5760 ltr.
c)
5846 ltr.
d)
6970 ltr.
|
|
Arnav Saini answered |
Given Data:
- Time taken to empty the tank with the break in the base: 6 hours
- Rate at which the channel funnel fills water: 4 liters per minute
- Time taken to empty the tank with the break in 8 hours
Calculating the Capacity of the Tank:
- Let the capacity of the tank be x liters.
- The tank is emptied in 6 hours with the break, so the leak rate = x/6 liters per hour
- The tank is filled by the channel funnel at a rate of 4 liters per minute = 240 liters per hour
- The net outflow rate due to the leak = 240 - x/6 liters per hour
- The tank is emptied in 8 hours, so the total outflow rate = x/8 liters per hour
- Equating the two outflow rates:
x/8 = 240 - x/6
Solving the above equation, we get x = 5760 liters
Therefore, the capacity of the tank is 5760 liters. Option B is the correct answer.
- Time taken to empty the tank with the break in the base: 6 hours
- Rate at which the channel funnel fills water: 4 liters per minute
- Time taken to empty the tank with the break in 8 hours
Calculating the Capacity of the Tank:
- Let the capacity of the tank be x liters.
- The tank is emptied in 6 hours with the break, so the leak rate = x/6 liters per hour
- The tank is filled by the channel funnel at a rate of 4 liters per minute = 240 liters per hour
- The net outflow rate due to the leak = 240 - x/6 liters per hour
- The tank is emptied in 8 hours, so the total outflow rate = x/8 liters per hour
- Equating the two outflow rates:
x/8 = 240 - x/6
Solving the above equation, we get x = 5760 liters
Therefore, the capacity of the tank is 5760 liters. Option B is the correct answer.
A tap can fill storage in 8 hours and another tap can discharge it in 16 hours. In the event that both the taps are open, the time taken to fill the tank will be:- a)8 hours
- b)10 hours
- c)16 hours
- d)24 hours
Correct answer is option 'C'. Can you explain this answer?
A tap can fill storage in 8 hours and another tap can discharge it in 16 hours. In the event that both the taps are open, the time taken to fill the tank will be:
a)
8 hours
b)
10 hours
c)
16 hours
d)
24 hours
|
|
Ishaan Roy answered |
Understanding the Problem
In this scenario, we have two taps: one that fills a tank and another that empties it.
Details of the Taps
- Filling Tap: Fills the tank in 8 hours.
- Discharging Tap: Empties the tank in 16 hours.
Calculating Rates of Work
- Filling Rate: The filling tap can fill 1 tank in 8 hours, which means it fills 1/8 of the tank in one hour.
- Discharging Rate: The discharging tap can empty 1 tank in 16 hours, meaning it empties 1/16 of the tank in one hour.
Combined Rate of Work
To find the combined effect of both taps working together, we add their rates:
- Net Filling Rate = Filling Rate - Discharging Rate
- Net Filling Rate = 1/8 - 1/16
Finding a Common Denominator
To perform this operation, we convert the fractions:
- 1/8 = 2/16
Now we can subtract:
- Net Filling Rate = 2/16 - 1/16 = 1/16
Time Taken to Fill the Tank
To find the time taken to fill the tank when both taps are open:
- If the net filling rate is 1/16 of the tank per hour, it will take 16 hours to fill 1 full tank.
Final Conclusion
Thus, when both taps are open, the time taken to fill the tank is 16 hours, confirming that option 'C' is correct.
In this scenario, we have two taps: one that fills a tank and another that empties it.
Details of the Taps
- Filling Tap: Fills the tank in 8 hours.
- Discharging Tap: Empties the tank in 16 hours.
Calculating Rates of Work
- Filling Rate: The filling tap can fill 1 tank in 8 hours, which means it fills 1/8 of the tank in one hour.
- Discharging Rate: The discharging tap can empty 1 tank in 16 hours, meaning it empties 1/16 of the tank in one hour.
Combined Rate of Work
To find the combined effect of both taps working together, we add their rates:
- Net Filling Rate = Filling Rate - Discharging Rate
- Net Filling Rate = 1/8 - 1/16
Finding a Common Denominator
To perform this operation, we convert the fractions:
- 1/8 = 2/16
Now we can subtract:
- Net Filling Rate = 2/16 - 1/16 = 1/16
Time Taken to Fill the Tank
To find the time taken to fill the tank when both taps are open:
- If the net filling rate is 1/16 of the tank per hour, it will take 16 hours to fill 1 full tank.
Final Conclusion
Thus, when both taps are open, the time taken to fill the tank is 16 hours, confirming that option 'C' is correct.
A cistern has 3 pipes A, B and C. A and B can ill it in 3 hours and 4 hours respectively while C can empty the completely filled cistern in 1 hour. If the pipes are opened in order at 3, 4 and 5 pm respectively, at what time will the cistern be empty?- a)7:12 PM
- b)6:15 PM
- c)8:12 PM
- d)8:35 PM
Correct answer is option 'A'. Can you explain this answer?
A cistern has 3 pipes A, B and C. A and B can ill it in 3 hours and 4 hours respectively while C can empty the completely filled cistern in 1 hour. If the pipes are opened in order at 3, 4 and 5 pm respectively, at what time will the cistern be empty?
a)
7:12 PM
b)
6:15 PM
c)
8:12 PM
d)
8:35 PM
|
|
Nilesh Banerjee answered |
Understanding the Problem
To solve the problem, we need to analyze the rates at which the pipes fill or empty the cistern and their operational timings.
Pipe Rates
- Pipe A can fill the cistern in 3 hours, so its rate is 1/3 of the cistern per hour.
- Pipe B can fill the cistern in 4 hours, so its rate is 1/4 of the cistern per hour.
- Pipe C can empty the cistern in 1 hour, so its rate is -1 (emptying) per hour.
Combined Rates of A and B
- When A and B are opened together:
- Rate of A + Rate of B = 1/3 + 1/4 = 4/12 + 3/12 = 7/12 of the cistern per hour.
Operational Sequence
- At 3 PM:
- Only Pipe A is open.
- In 1 hour (from 3 PM to 4 PM), it fills 1/3 of the cistern.
- At 4 PM:
- Pipes A and B are open.
- They fill together at a rate of 7/12 of the cistern per hour.
- From 4 PM to 5 PM (1 hour), they fill 7/12 of the cistern.
- Total filled by 5 PM: 1/3 + 7/12 = 4/12 + 7/12 = 11/12 of the cistern.
- At 5 PM:
- All pipes A, B, and C are open.
- The combined rate is (7/12 - 1) = 7/12 - 12/12 = -5/12 (emptying at this rate).
Time to Empty the Cistern
- From 5 PM, 1/12 of the cistern remains.
- Time taken to empty 1/12 at -5/12 rate = (1/12) / (5/12) = 1/5 hours = 12 minutes.
Final Calculation
- 5 PM + 12 minutes = 5:12 PM.
- Therefore, the cistern will be empty by 7:12 PM.
Thus, the correct answer is option 'A': 7:12 PM.
To solve the problem, we need to analyze the rates at which the pipes fill or empty the cistern and their operational timings.
Pipe Rates
- Pipe A can fill the cistern in 3 hours, so its rate is 1/3 of the cistern per hour.
- Pipe B can fill the cistern in 4 hours, so its rate is 1/4 of the cistern per hour.
- Pipe C can empty the cistern in 1 hour, so its rate is -1 (emptying) per hour.
Combined Rates of A and B
- When A and B are opened together:
- Rate of A + Rate of B = 1/3 + 1/4 = 4/12 + 3/12 = 7/12 of the cistern per hour.
Operational Sequence
- At 3 PM:
- Only Pipe A is open.
- In 1 hour (from 3 PM to 4 PM), it fills 1/3 of the cistern.
- At 4 PM:
- Pipes A and B are open.
- They fill together at a rate of 7/12 of the cistern per hour.
- From 4 PM to 5 PM (1 hour), they fill 7/12 of the cistern.
- Total filled by 5 PM: 1/3 + 7/12 = 4/12 + 7/12 = 11/12 of the cistern.
- At 5 PM:
- All pipes A, B, and C are open.
- The combined rate is (7/12 - 1) = 7/12 - 12/12 = -5/12 (emptying at this rate).
Time to Empty the Cistern
- From 5 PM, 1/12 of the cistern remains.
- Time taken to empty 1/12 at -5/12 rate = (1/12) / (5/12) = 1/5 hours = 12 minutes.
Final Calculation
- 5 PM + 12 minutes = 5:12 PM.
- Therefore, the cistern will be empty by 7:12 PM.
Thus, the correct answer is option 'A': 7:12 PM.
Two pipes can fill a cistern separately in 10 hours and 15 hours. They can together fill the cistern in- a)9 hours
- b)6 hours
- c)7 hours
- d)8 hours
Correct answer is option 'B'. Can you explain this answer?
Two pipes can fill a cistern separately in 10 hours and 15 hours. They can together fill the cistern in
a)
9 hours
b)
6 hours
c)
7 hours
d)
8 hours
|
Abhiram Mehra answered |
Understanding the Problem
To solve the problem of how long two pipes can fill a cistern together, we start by determining their individual filling rates.
Individual Filling Rates
- Pipe A can fill the cistern in 10 hours. Therefore, its rate is 1/10 cisterns per hour.
- Pipe B can fill the cistern in 15 hours. Hence, its rate is 1/15 cisterns per hour.
Combined Filling Rate
To find the combined rate of both pipes, we add their individual rates:
- Combined rate = Rate of Pipe A + Rate of Pipe B
- Combined rate = 1/10 + 1/15
To perform this addition, we need a common denominator. The least common multiple of 10 and 15 is 30.
- 1/10 = 3/30
- 1/15 = 2/30
Now, adding these rates:
- Combined rate = 3/30 + 2/30 = 5/30 = 1/6
Time to Fill the Cistern Together
The combined rate of 1/6 means that together, the two pipes can fill 1 cistern in 6 hours.
Conclusion
The correct answer is option 'B', as the two pipes working together can fill the cistern in 6 hours.
To solve the problem of how long two pipes can fill a cistern together, we start by determining their individual filling rates.
Individual Filling Rates
- Pipe A can fill the cistern in 10 hours. Therefore, its rate is 1/10 cisterns per hour.
- Pipe B can fill the cistern in 15 hours. Hence, its rate is 1/15 cisterns per hour.
Combined Filling Rate
To find the combined rate of both pipes, we add their individual rates:
- Combined rate = Rate of Pipe A + Rate of Pipe B
- Combined rate = 1/10 + 1/15
To perform this addition, we need a common denominator. The least common multiple of 10 and 15 is 30.
- 1/10 = 3/30
- 1/15 = 2/30
Now, adding these rates:
- Combined rate = 3/30 + 2/30 = 5/30 = 1/6
Time to Fill the Cistern Together
The combined rate of 1/6 means that together, the two pipes can fill 1 cistern in 6 hours.
Conclusion
The correct answer is option 'B', as the two pipes working together can fill the cistern in 6 hours.
Two pipes, P and Q, together can fill a cistern in 20 minutes and P alone can in 30 minutes. Then Q alone can fill the cistern in- a)51 minutes
- b)62 minutes
- c)60 minutes
- d)61 minutes
Correct answer is option 'C'. Can you explain this answer?
Two pipes, P and Q, together can fill a cistern in 20 minutes and P alone can in 30 minutes. Then Q alone can fill the cistern in
a)
51 minutes
b)
62 minutes
c)
60 minutes
d)
61 minutes
|
Ssc Cgl answered |
Using Rule 7,
Part of the cistern filled by pipe Q in 1 minute
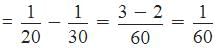
Required time = 60 minutes
Part of the cistern filled by pipe Q in 1 minute
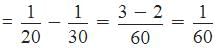
Required time = 60 minutes
Two pipes A and B can separately fill a tank in 2 hours and 3 hours respectively. If both the pipes are opened simultaneously in the empty tank, then the tank will be filled in- a)1 hour 20 minutes
- b)1 hour 12 minutes
- c)2 hours 30 minutes
- d)1 hour 15 minutes
Correct answer is option 'B'. Can you explain this answer?
Two pipes A and B can separately fill a tank in 2 hours and 3 hours respectively. If both the pipes are opened simultaneously in the empty tank, then the tank will be filled in
a)
1 hour 20 minutes
b)
1 hour 12 minutes
c)
2 hours 30 minutes
d)
1 hour 15 minutes
|
|
Ssc Cgl answered |
Using Rule 1,
Part of tank filled by pipes A and B in 1 hour
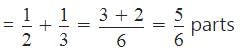
Required time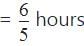
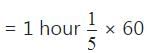
= 1 hour 12 minutes
Part of tank filled by pipes A and B in 1 hour
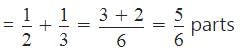
Required time
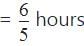
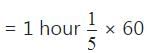
= 1 hour 12 minutes
A water tank can be filled by a tap in 30 minutes and another tap can fill it in 60 minutes. If both the taps are kept open for 5 minutes and then the first tap is closed, how long will it take for the tank to be full ?- a)45 minutes
- b)20 minutes
- c)25 minutes
- d)30 minutes
Correct answer is option 'A'. Can you explain this answer?
A water tank can be filled by a tap in 30 minutes and another tap can fill it in 60 minutes. If both the taps are kept open for 5 minutes and then the first tap is closed, how long will it take for the tank to be full ?
a)
45 minutes
b)
20 minutes
c)
25 minutes
d)
30 minutes
|
|
Ssc Cgl answered |
Using Rule 2,
Part of the tank filled by both taps in 5 minutes
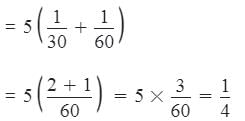
Remaining part =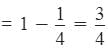
that is filled by second tap.
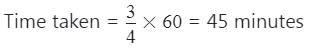
Part of the tank filled by both taps in 5 minutes
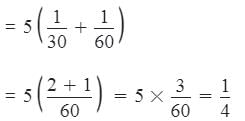
Remaining part =
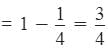that is filled by second tap.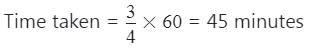A tap can fill a cistern in 8 hours and another tap can empty it in 16 hours. If both the taps are open, the time (in hours) taken to fill the tank will be :- a)24
- b)8
- c)10
- d)16
Correct answer is option 'D'. Can you explain this answer?
A tap can fill a cistern in 8 hours and another tap can empty it in 16 hours. If both the taps are open, the time (in hours) taken to fill the tank will be :
a)
24
b)
8
c)
10
d)
16
|
|
Ssc Cgl answered |
Part of the cistern filled in 1 hour = 1/8
Part of the cistern emptied in 1 hour = 1/16
When both the taps are opened simultaneously, part of cistern filled in 1 hour
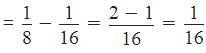
Hence, the cistern will be filled in 16 hours.
Using Rule 7,
Here, x = 8, y = 16
Required time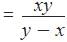
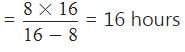
Part of the cistern emptied in 1 hour = 1/16
When both the taps are opened simultaneously, part of cistern filled in 1 hour
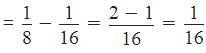
Hence, the cistern will be filled in 16 hours.
Using Rule 7,
Here, x = 8, y = 16
Required time
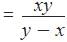
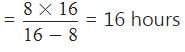
Three pipes P, Q and R can separately fill a cistern in 4,8 and 12 hours respectively. Another pipe S can empty the completely filled cistern in10 hours. Which of the following arrangements will fill the empty cistern in less time than others ?- a)P, Q and S are open.
- b)Q alone is open.
- c)P and S are open.
- d)P, R and S are open.
Correct answer is option 'A'. Can you explain this answer?
Three pipes P, Q and R can separately fill a cistern in 4,8 and 12 hours respectively. Another pipe S can empty the completely filled cistern in10 hours. Which of the following arrangements will fill the empty cistern in less time than others ?
a)
P, Q and S are open.
b)
Q alone is open.
c)
P and S are open.
d)
P, R and S are open.
|
|
EduRev SSC CGL answered |
Using Rule 2 and 7,
Part of the cistern filled in 1 hour
when pipes P and S are open
Hence, the cistern will be filled in 20/3 hours ≈ 6.6 hours
Part of the cistern filled in 1 hour
when pipes P, R and S are open
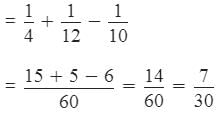
Hence, the cistern will be filled in 30/7 hours ≈ 4.3 hours
Part of the cistern filled in I hour
when pipes P, Q and S are open
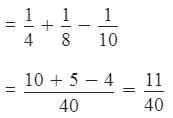
Hence, the cistern will be filled in 40/11 hours ≈ 3.6 hours
Cistern can be filled faster when P, Q & S are open
Part of the cistern filled in 1 hour
when pipes P and S are open
Hence, the cistern will be filled in 20/3 hours ≈ 6.6 hours
Part of the cistern filled in 1 hour
when pipes P, R and S are open
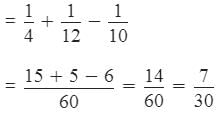
Hence, the cistern will be filled in 30/7 hours ≈ 4.3 hours
Part of the cistern filled in I hour
when pipes P, Q and S are open
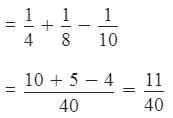
Hence, the cistern will be filled in 40/11 hours ≈ 3.6 hours
Cistern can be filled faster when P, Q & S are open
One tap can fill a water tank in 40 minutes and another tap can make the filled tank empty in 60 minutes. If both the taps are open, in how many hours will the empty tank be filled ?- a)3.5 hours
- b)2 hours
- c)2.5 hours
- d)3 hours
Correct answer is option 'B'. Can you explain this answer?
One tap can fill a water tank in 40 minutes and another tap can make the filled tank empty in 60 minutes. If both the taps are open, in how many hours will the empty tank be filled ?
a)
3.5 hours
b)
2 hours
c)
2.5 hours
d)
3 hours
|
|
Pioneer Academy answered |
Using Rule 7,
Part of the tank filled when both taps are opened together
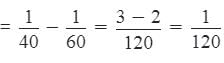
Hence, the tank will be filled in 120 minutes 2 hours.
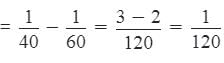
Hence, the tank will be filled in 120 minutes 2 hours.
Two pipes can fill a cistern in 3 hours and 4 hours respectively and a waste pipe can empty it in 2 hours. If all the three pipes are kept open, then the cistern will be filled in :- a)12 hours
- b)5 hours
- c)8 hours
- d)10 hours
Correct answer is option 'A'. Can you explain this answer?
Two pipes can fill a cistern in 3 hours and 4 hours respectively and a waste pipe can empty it in 2 hours. If all the three pipes are kept open, then the cistern will be filled in :
a)
12 hours
b)
5 hours
c)
8 hours
d)
10 hours
|
|
Pioneer Academy answered |
Using Rule 2,
Part of the cistern filled in 1 hour
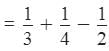
[Cistern filled by 1st pipe + Cistern filled by 2nd pipe - Cistern emptied by 3rd pipe]
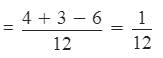
Hence, the cistern will be filled in 12 hours.
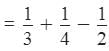
[Cistern filled by 1st pipe + Cistern filled by 2nd pipe - Cistern emptied by 3rd pipe]
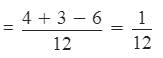
Hence, the cistern will be filled in 12 hours.
Two pipes can fill a tank in 15 hours and 20 hours respectively, while the third can empty it in 30 hours. If all the pipes are opened simultaneously, the empty tank will be filled in- a)
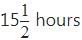
- b)10 hours
- c)12 hours
- d)15 hours
Correct answer is option 'C'. Can you explain this answer?
Two pipes can fill a tank in 15 hours and 20 hours respectively, while the third can empty it in 30 hours. If all the pipes are opened simultaneously, the empty tank will be filled in
a)
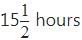
b)
10 hours
c)
12 hours
d)
15 hours
|
|
Ssc Cgl answered |
Using Rule 2,
Part of tank filled in 1 hour when all three pipes are opened simultaneously
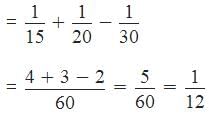
Hence, the tank will be filled in 12 hours.
Part of tank filled in 1 hour when all three pipes are opened simultaneously
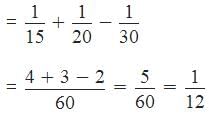
Hence, the tank will be filled in 12 hours.
A tank is fitted with two taps A and B. A can fill the tank totally in 45 minutes and B can purge the full tank in 60 minutes. On the off chance that both the taps are opened on the other hand for 1 minute, then in what amount of time the unfilled tank will be filled totally?- a)2 hrs 55 min
- b)3 hrs 40 min
- c)5 hrs 53 min
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
A tank is fitted with two taps A and B. A can fill the tank totally in 45 minutes and B can purge the full tank in 60 minutes. On the off chance that both the taps are opened on the other hand for 1 minute, then in what amount of time the unfilled tank will be filled totally?
a)
2 hrs 55 min
b)
3 hrs 40 min
c)
5 hrs 53 min
d)
none of these
|
|
Pioneer Academy answered |
Work done by A in 1st minutes and B 2nd minute = (1/45- 1/60)= 1/180
Part filled in 2 min = 1/180
Part filled in 358 min = (1/360*358) = 358/360 = 179/180
Remaining part = (1-179/180) = 1/180
1/45 part is filled by A in (45*1/180) min= 1/4 min.
Total time taken to fill it = 358 1/4 min = 5 hrs.58 min 15 sec.
Part filled in 2 min = 1/180
Part filled in 358 min = (1/360*358) = 358/360 = 179/180
Remaining part = (1-179/180) = 1/180
1/45 part is filled by A in (45*1/180) min= 1/4 min.
Total time taken to fill it = 358 1/4 min = 5 hrs.58 min 15 sec.
A substantial tanker can be filled by two pipes A and B in an hour and 40 minutes separately. How long will it take to fill the tanker from unfilled state if B is utilized for a fraction of the time and A and B fill it together for the other half?- a)15 min.
- b)20 min.
- c)27.5 min.
- d)30 min.
Correct answer is option 'D'. Can you explain this answer?
A substantial tanker can be filled by two pipes A and B in an hour and 40 minutes separately. How long will it take to fill the tanker from unfilled state if B is utilized for a fraction of the time and A and B fill it together for the other half?
a)
15 min.
b)
20 min.
c)
27.5 min.
d)
30 min.
|
|
EduRev SSC CGL answered |
Let the total time taken be x minute. Then,
(1/40*x/2) + (1/60+ 1/40) x/2= 1 ⇒ x/80 + x/48 = 1
⇒3x+ 5x= 240 ⇒8x= 240 ⇒x= 30
Hence, the required time is 30 minutes.
(1/40*x/2) + (1/60+ 1/40) x/2= 1 ⇒ x/80 + x/48 = 1
⇒3x+ 5x= 240 ⇒8x= 240 ⇒x= 30
Hence, the required time is 30 minutes.
A channels can fill a tank in x hours and another funnel can exhaust it in y (y>x) hours. In the event that both the funnels are open, in how long will the tank be filled?- a)(x-y) hours
- b)(y-x) hours
- c)xy/(x-y) hours
- d)xy/(y-x) hours
Correct answer is option 'D'. Can you explain this answer?
A channels can fill a tank in x hours and another funnel can exhaust it in y (y>x) hours. In the event that both the funnels are open, in how long will the tank be filled?
a)
(x-y) hours
b)
(y-x) hours
c)
xy/(x-y) hours
d)
xy/(y-x) hours
|
|
EduRev SSC CGL answered |
Work done by filling pipe in 1 hr = 1/x
Work done by emptying pipe in 1 hr = 1/y
Net filling work done by both in 1 hr = (1/x- 1/y) = (y-x)/xy
∴ The tank will be filled in xy/(y-x) hrs.
Work done by emptying pipe in 1 hr = 1/y
Net filling work done by both in 1 hr = (1/x- 1/y) = (y-x)/xy
∴ The tank will be filled in xy/(y-x) hrs.
A pipe can fill a tank in ‘x’ hours and another pipe can empty it in‘y’ (y > x) hours. If both the pipes are open, in how many hours will the tank be filled ?- a)
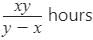
- b)(x - y) hours
- c)(y - x) hours
- d)
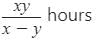
Correct answer is option 'A'. Can you explain this answer?
A pipe can fill a tank in ‘x’ hours and another pipe can empty it in‘y’ (y > x) hours. If both the pipes are open, in how many hours will the tank be filled ?
a)
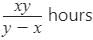
b)
(x - y) hours
c)
(y - x) hours
d)
|
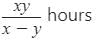
Bayshore Academy answered |
Part of the tank filled in 1 hour = 1/x
Part of the tank emptied in 1 hour = 1/y
Part of the tank filled in 1 hour
when both are opened
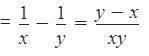
Tank will be filled in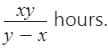
Part of the tank emptied in 1 hour = 1/y
Part of the tank filled in 1 hour
when both are opened
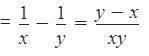
Tank will be filled in
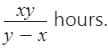
Two pipes A and B can fill a tank in 36 minutes and 45 minutes respectively. Another pipe C can empty the tank in 30 minutes. First A and B are opened. After 7 minutes, C is also opened. The tank is filled up in- a)45 minutes
- b)39 minutes
- c)46 minutes
- d)40 minutes
Correct answer is option 'C'. Can you explain this answer?
Two pipes A and B can fill a tank in 36 minutes and 45 minutes respectively. Another pipe C can empty the tank in 30 minutes. First A and B are opened. After 7 minutes, C is also opened. The tank is filled up in
a)
45 minutes
b)
39 minutes
c)
46 minutes
d)
40 minutes
|
|
Ssc Cgl answered |
Part of the tank filled by pipes A and B in 1 minute
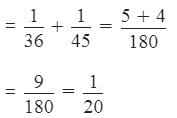
Part of the tank filled by these pipes in 7 minutes
= 7/20
Remaining unfilled part
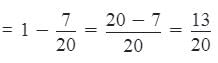
When all three pipes are opened.
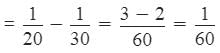
Time taken in filling 13/20 part
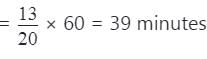
Required time = 39 + 7 = 46 minutes
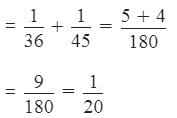
Part of the tank filled by these pipes in 7 minutes
= 7/20
Remaining unfilled part
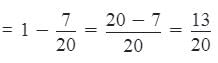
When all three pipes are opened.
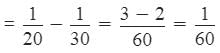
Time taken in filling 13/20 part
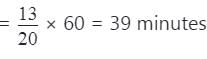
Required time = 39 + 7 = 46 minutes
A pipe can fill a tank in x hours and another can empty it in y hours. They can together fill it in (y > x)- a)
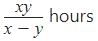
- b)
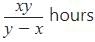
- c)x - y hours
- d)y - x hours
Correct answer is option 'B'. Can you explain this answer?
A pipe can fill a tank in x hours and another can empty it in y hours. They can together fill it in (y > x)
a)
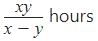
b)
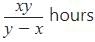
c)
x - y hours
d)
y - x hours
|
Glance Learning Institute answered |
When both pipes are opened simultaneously, part of the tank filled in 1 hour
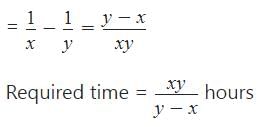
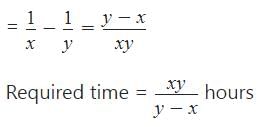
Two pipes A and B can separately fill a cistern in 60 minutes and 75 minutes respectively. There is a third pipe in the bottom of the cistern to empty it. If all the three pipes are simultaneously opened, then the cistern is full in 50 minutes. In how much time the third pipe alone can empty the cistern?- a)90 minutes
- b)110 minutes
- c)100 minutes
- d)120 minutes
Correct answer is option 'C'. Can you explain this answer?
Two pipes A and B can separately fill a cistern in 60 minutes and 75 minutes respectively. There is a third pipe in the bottom of the cistern to empty it. If all the three pipes are simultaneously opened, then the cistern is full in 50 minutes. In how much time the third pipe alone can empty the cistern?
a)
90 minutes
b)
110 minutes
c)
100 minutes
d)
120 minutes
|
|
Pioneer Academy answered |
Let the third pipe empty the cistern in x minutes.
Part of cistern filled in 1 minute when all three pipes are opened simultaneously
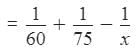
According to the question,
Part of cistern filled in 1 minute when all three pipes are opened simultaneously
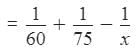
According to the question,
12 pumps working 6 hours a day can empty a completely filled reservoir in 15 days. How many such pumps working 9 hours a day will empty the same reservoir in 12 days ?- a)12
- b)15
- c)9
- d)10
Correct answer is option 'D'. Can you explain this answer?
12 pumps working 6 hours a day can empty a completely filled reservoir in 15 days. How many such pumps working 9 hours a day will empty the same reservoir in 12 days ?
a)
12
b)
15
c)
9
d)
10
|
|
Ssc Cgl answered |
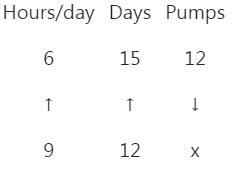
Let x be number of pumps
9 : 6 : : 12 : x = 12 : 15 : : 12 : x
9 × 12 × x = 6 × 12 × 15
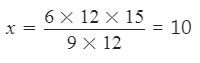
Two pipes A and B can fill a water tank in 20 and 24 min respectively. A third pipe C can empty at the rate of 3 gallons per minute. If A, B and C opened together fill the tank in 15 min, the capacity of the tank (in gallons) is:- a)180
- b)150
- c)120
- d)60
Correct answer is option 'C'. Can you explain this answer?
Two pipes A and B can fill a water tank in 20 and 24 min respectively. A third pipe C can empty at the rate of 3 gallons per minute. If A, B and C opened together fill the tank in 15 min, the capacity of the tank (in gallons) is:
a)
180
b)
150
c)
120
d)
60
|
|
Pioneer Academy answered |
Let the capacity of the tank = x gallons
Quantity of the water filled in the tank in 1 min when all the pipes A, B and C are opened simultaneously= x/20 + x/24 - 3
According to question,
x/20 + x/24 - 3 = x/15
or, x/20 + x/24 - x/15 = 3
or, (6x + 5x - 8x)/120 = 3
or, 3x/120 = 3
or, x = 120 gallons
Quantity of the water filled in the tank in 1 min when all the pipes A, B and C are opened simultaneously= x/20 + x/24 - 3
According to question,
x/20 + x/24 - 3 = x/15
or, x/20 + x/24 - x/15 = 3
or, (6x + 5x - 8x)/120 = 3
or, 3x/120 = 3
or, x = 120 gallons
Pipe A can fill an empty tank in 6 hours and pipe B in 8 hours. If both the pipes are opened and after 2 hours pipe. A is closed, how much time B will take to fill the remaining tank?- a)
- b)
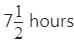
- c)
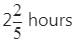
- d)
Correct answer is option 'A'. Can you explain this answer?
Pipe A can fill an empty tank in 6 hours and pipe B in 8 hours. If both the pipes are opened and after 2 hours pipe. A is closed, how much time B will take to fill the remaining tank?
a)
b)
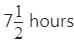
c)
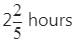
d)
|
|
Pioneer Academy answered |
Using Rule 1,
Part of tank filled by pipes A and B in 2 hours
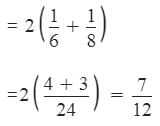
Remaining part =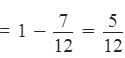
This part is filled by pipe B.
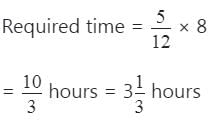
Part of tank filled by pipes A and B in 2 hours
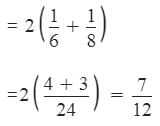
Remaining part =
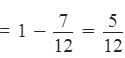
This part is filled by pipe B.
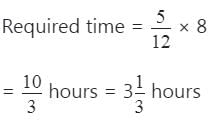
Chapter doubts & questions for Pipes and Cistern - Quantitative Aptitude for Competitive Examinations 2025 is part of Bank Exams exam preparation. The chapters have been prepared according to the Bank Exams exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Bank Exams 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Pipes and Cistern - Quantitative Aptitude for Competitive Examinations in English & Hindi are available as part of Bank Exams exam.
Download more important topics, notes, lectures and mock test series for Bank Exams Exam by signing up for free.
Quantitative Aptitude for Competitive Examinations
166 videos|137 docs|171 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup