All Exams >
Bank Exams >
Quantitative Aptitude for Competitive Examinations >
All Questions
All questions of Age for Bank Exams Exam
The age of father 10 years ago was thrice the age of his son. Ten years hence, father’s age will be twice that of his son. The ratio of their present ages is- a)5:2
- b)7:3
- c)9:2
- d)13:4
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The age of father 10 years ago was thrice the age of his son. Ten years hence, father’s age will be twice that of his son. The ratio of their present ages is
a)
5:2
b)
7:3
c)
9:2
d)
13:4
e)
None of these

|
Future Foundation Institute answered |
The correct option ia B.
Let the ages of father and son 10 years ago be 3x and x years respectively.
Then, (3x + 10) + 10 = 2[(x + 10) + 10]
⇒ 3x + 20 = 2x + 40
⇒ x = 20
∴ Required ratio
= (3x + 10) : (x + 10)
= 70 : 30
= 7 : 3
Let the ages of father and son 10 years ago be 3x and x years respectively.
Then, (3x + 10) + 10 = 2[(x + 10) + 10]
⇒ 3x + 20 = 2x + 40
⇒ x = 20
∴ Required ratio
= (3x + 10) : (x + 10)
= 70 : 30
= 7 : 3
The ratio between the present ages of Ravi and Vinay is 7:15 respectively. Two years from now Vinay’s age will be twice that of Ravi’s age. What was the difference between their ages 5 years ago.- a)13 years
- b)16 years
- c)11 years
- d)18 years
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The ratio between the present ages of Ravi and Vinay is 7:15 respectively. Two years from now Vinay’s age will be twice that of Ravi’s age. What was the difference between their ages 5 years ago.
a)
13 years
b)
16 years
c)
11 years
d)
18 years
e)
None of these

|
Aspire Academy answered |
The correct option is B.
Let the present age of Ravi be 7x and that of Vinay be 15x.
After 2 yrs , Ravi age = 7x+2
Vinay age = 15x+2.
Acc. to ques,
15x+2 = 2 (7x+2)
15x+2 = 14x+4
x = 2.
Five yrs ago,
Ravi age = 7x-5 => 7*2 - 5 = 9 yrs
Vinay age = 15x - 5 = 15*2 - 5 = 25 yrs.
Difference = 25 - 9 = 16 years
Let the present age of Ravi be 7x and that of Vinay be 15x.
After 2 yrs , Ravi age = 7x+2
Vinay age = 15x+2.
Acc. to ques,
15x+2 = 2 (7x+2)
15x+2 = 14x+4
x = 2.
Five yrs ago,
Ravi age = 7x-5 => 7*2 - 5 = 9 yrs
Vinay age = 15x - 5 = 15*2 - 5 = 25 yrs.
Difference = 25 - 9 = 16 years
The ratio between the present ages of P and Q is 6:7. If Q is four years older than P, what will be the ratio of the ages of P and Q after 4 years?
- a)3:4
- b)3:5
- c)4:3
- d)Data inadequate
- e)None of these
Correct answer is option 'E'. Can you explain this answer?
The ratio between the present ages of P and Q is 6:7. If Q is four years older than P, what will be the ratio of the ages of P and Q after 4 years?
a)
3:4
b)
3:5
c)
4:3
d)
Data inadequate
e)
None of these

|
Aishwarya Rajput answered |
P:Q = 6:7 i.e P/Q = 6/7 => 7P = 6Q--------1
Given that Q = P + 4 (put in 1)
7P = 6(P + 4)
So, P = 24 and Q = P+4 i.e 28years
After 4 years, P+4 i.e 24+4= 28yrs
And Q = 28 +4 = 32years
The ratio we get is 7:8
The total age of A and B is 12 years more than the total age of B and C. C is how many years younger than A?- a)12 years
- b)24 years
- c)C is elder than A
- d)Data inadequate
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
The total age of A and B is 12 years more than the total age of B and C. C is how many years younger than A?
a)
12 years
b)
24 years
c)
C is elder than A
d)
Data inadequate
e)
None of these

|
Glance Learning Institute answered |
The correct option is A.
Given that A+B = 12 + B + C
⇒ A – C = 12 + B – B = 12
⇒ C is younger than A by 12 years
Given that A+B = 12 + B + C
⇒ A – C = 12 + B – B = 12
⇒ C is younger than A by 12 years
Ayesha’s father was 38 year of age when she was born. Her mother was 36 years old when her brother, four years younger to her, was born, What was the age of Ayesha’s father and mother respectively when her brother was born.- a)32 years, 23 years
- b)32 years, 29 years
- c)35 years, 29 years
- d)35 years, 33 years
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
Ayesha’s father was 38 year of age when she was born. Her mother was 36 years old when her brother, four years younger to her, was born, What was the age of Ayesha’s father and mother respectively when her brother was born.
a)
32 years, 23 years
b)
32 years, 29 years
c)
35 years, 29 years
d)
35 years, 33 years
e)
None of these
|
|
Dia Mehta answered |
Mother's age when Ayesha's brother was born = 36 years.
Father's age when Ayesha's brother was born = (38 + 4) years = 42 years.
 Required difference = (42 - 36) years = 6 years.
Required difference = (42 - 36) years = 6 years.In a family the average age of the father and mother is 38 years, whereas the average age of father, mother and only daughter is 28 years. The age of daughters is- a)5 years
- b)6 years
- c)8 years
- d)10 years
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
In a family the average age of the father and mother is 38 years, whereas the average age of father, mother and only daughter is 28 years. The age of daughters is
a)
5 years
b)
6 years
c)
8 years
d)
10 years
e)
None of these
|
|
Anaya Patel answered |
The correct option is C.
Let father's age be x, mother's age be y and daughter's age be z.
(x+y)/2 = 38
x+y = 76
(x+y+z)/3 = 28
(76+z)/3 = 28
76+z = 84
z = 8 years
Let father's age be x, mother's age be y and daughter's age be z.
(x+y)/2 = 38
x+y = 76
(x+y+z)/3 = 28
(76+z)/3 = 28
76+z = 84
z = 8 years
The average age of a man and his son is 54 years. The ratio of their ages is 23: 13. What will be the ratio of their ages after 6 years.
- a)10:7
- b)5:3
- c)4:3
- d)3:2
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The average age of a man and his son is 54 years. The ratio of their ages is 23: 13. What will be the ratio of their ages after 6 years.
a)
10:7
b)
5:3
c)
4:3
d)
3:2
e)
None of these

|
Vertex Academy answered |
To find the ratio of their ages after 6 years:
- Let the current ages be 23x and 13x.
avg age =sum/2
sum = avg age x 2
sum = 54x2 =108
- Their sum is 36x (23x + 13x = 36x), and this equals 108 years.
- So, 36x = 108 years, thus x = 3.
- After 6 years, their ages will be 23(3) + 6 = 75 and 13(3) + 6 = 45.
- The ratio of their ages after 6 years is 75:45, which simplifies to 5:3.
- This simplifies further to 5:3, which is the correct answer (Option B).
- Let the current ages be 23x and 13x.
avg age =sum/2
sum = avg age x 2
sum = 54x2 =108
- Their sum is 36x (23x + 13x = 36x), and this equals 108 years.
- So, 36x = 108 years, thus x = 3.
- After 6 years, their ages will be 23(3) + 6 = 75 and 13(3) + 6 = 45.
- The ratio of their ages after 6 years is 75:45, which simplifies to 5:3.
- This simplifies further to 5:3, which is the correct answer (Option B).
If 6 years are subtracted from the present age of Gagan and the remainder is divided by 18,then the present age of his grandson Anup is obtained. If Anup is 2 years younger to Madan whose age is 5 years,then what is Gagan's present age?- a)48 years
- b)60 years
- c)84 years
- d)96 years
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
If 6 years are subtracted from the present age of Gagan and the remainder is divided by 18,then the present age of his grandson Anup is obtained. If Anup is 2 years younger to Madan whose age is 5 years,then what is Gagan's present age?
a)
48 years
b)
60 years
c)
84 years
d)
96 years
e)
None of these
|
|
Anaya Patel answered |
The correct option is B.
Let gagan's age be "x".
anup's age = (x-6)/18
madan's age=5 therefore anup's age =3
btp,
(x-6)/18=3
so x=60
Let gagan's age be "x".
anup's age = (x-6)/18
madan's age=5 therefore anup's age =3
btp,
(x-6)/18=3
so x=60
The ratio between the present age of Radha and Seema is 5:4. Four years ago Seema’s age was 24 years. What will be the age of Radha after 5 years.- a)39 years
- b)40 years
- c)32 years
- d)35 years
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The ratio between the present age of Radha and Seema is 5:4. Four years ago Seema’s age was 24 years. What will be the age of Radha after 5 years.
a)
39 years
b)
40 years
c)
32 years
d)
35 years
e)
None of these

|
Anannya Reddy answered |
Radha and seema present age =5x, 4x
4years ago seema age =24
so 4x-4=24
4x=28
x=7 so present age of radha=35 seema =28
so 5years after =35+5=40 so B is the answer
4years ago seema age =24
so 4x-4=24
4x=28
x=7 so present age of radha=35 seema =28
so 5years after =35+5=40 so B is the answer
The ratio between the present ages of Radha and Seema is 5:7. After 8 years Radha’s age will be 28 years. What was Seema’s age 5 years ago.- a)21 years
- b)24 years
- c)28 years
- d)22 years
- e)None of these
Correct answer is option 'E'. Can you explain this answer?
The ratio between the present ages of Radha and Seema is 5:7. After 8 years Radha’s age will be 28 years. What was Seema’s age 5 years ago.
a)
21 years
b)
24 years
c)
28 years
d)
22 years
e)
None of these
|
|
Anaya Patel answered |
The correct option is E.
Let the present age of Radha be 5x So 8 yrs back , i.e, at present she is 20.
this means 5x = 20 => x = 4
Then Seema 's age = 7x = 7*4 = 28yrs.
Five yrs ago , her age was 28 - 5 = 23yrs.
Let the present age of Radha be 5x So 8 yrs back , i.e, at present she is 20.
this means 5x = 20 => x = 4
Then Seema 's age = 7x = 7*4 = 28yrs.
Five yrs ago , her age was 28 - 5 = 23yrs.
Two years ago the ratio of ages of A and B was 5:7. Two years hence the ratio of their ages will be 7:9. What is the present age of B.
- a)16 years
- b)14.5 years
- c)12 years
- d)15 years
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
Two years ago the ratio of ages of A and B was 5:7. Two years hence the ratio of their ages will be 7:9. What is the present age of B.
a)
16 years
b)
14.5 years
c)
12 years
d)
15 years
e)
None of these

|
Glance Learning Institute answered |
Let x,y be present ages of A,B.
x-2/y-2=5/7 implies 7x-5y=4 -(1)
x+2/y+2=7/9 implies 9x-7y=-4. (2)
(1) * 7 - (2) * 5 gives x=12
7(12) - 5y = 4
84 - 5y = 4
80 = 5y
16 = y
substitute and get y which would be 16
x-2/y-2=5/7 implies 7x-5y=4 -(1)
x+2/y+2=7/9 implies 9x-7y=-4. (2)
(1) * 7 - (2) * 5 gives x=12
7(12) - 5y = 4
84 - 5y = 4
80 = 5y
16 = y
substitute and get y which would be 16
On Teacher’s Day, 4800 sweets were to be equally distributed among a certain number of children. But on that particular day 100 children were absent. Hence, each child got four sweets extra. How many children were originally supposed to be there?- a)300
- b)400
- c)540
- d) 500
- e)None of these .
Correct answer is option 'B'. Can you explain this answer?
On Teacher’s Day, 4800 sweets were to be equally distributed among a certain number of children. But on that particular day 100 children were absent. Hence, each child got four sweets extra. How many children were originally supposed to be there?
a)
300
b)
400
c)
540
d)
500
e)
None of these .

|
Tanvi Dey answered |
Let the original number of children be x.
∴ 4800/x-100 - 4800/x = 4
=> 4800((x-x+100)/(x(x-100))) = 4
=> x(x-100) = 1200 * 100
=> x(x-100) = 400(400-100)
=> x = 400
The average age of a man and his two twin sons is 30 years. The ratio of the ages of father and one of his sons is 5:2. What is the father’s age- a)50 years
- b)30 years
- c)45 years
- d)20 years
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
The average age of a man and his two twin sons is 30 years. The ratio of the ages of father and one of his sons is 5:2. What is the father’s age
a)
50 years
b)
30 years
c)
45 years
d)
20 years
e)
None of these

|
Aishwarya Rajput answered |
Let father's age be M and age of twins be 2x
(M + 2x)/3 = 30
M + 2x = 90------------(1)
M/x = 5/2
2M = 5x---------------(2)
Multiply (1) with 2
We get, 2M + 4x = 180--------------(3)
Putting (2) in (3)
5x+4x = 180 => 9x = 180x = 20. [his children are twins so 2x = 40]Since M + 2x = 90M = 90 -40 = 50years
(M + 2x)/3 = 30
M + 2x = 90------------(1)
M/x = 5/2
2M = 5x---------------(2)
Multiply (1) with 2
We get, 2M + 4x = 180--------------(3)
Putting (2) in (3)
5x+4x = 180 => 9x = 180x = 20. [his children are twins so 2x = 40]Since M + 2x = 90M = 90 -40 = 50years
A father said to his son, “At the time of your birth, I was as old as you are at present”. If father’s age is 38 years now the sons age 5 years back was- a)14 years
- b)19 years
- c)33 years
- d)38 years
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A father said to his son, “At the time of your birth, I was as old as you are at present”. If father’s age is 38 years now the sons age 5 years back was
a)
14 years
b)
19 years
c)
33 years
d)
38 years
e)
None of these
|
|
Prani Garg answered |
HERE IS YOUR ANSWER.
Let the present age of son= x
At the time of birth of son,father age = x
So after x yrs i.e. at present age of father= 38
38=x+x
x= 38÷2= 19
So the present age of son is 19
Age of son before 5 yrs= 19-5= 14 yrs.
HOPE IT HELPS.
Let the present age of son= x
At the time of birth of son,father age = x
So after x yrs i.e. at present age of father= 38
38=x+x
x= 38÷2= 19
So the present age of son is 19
Age of son before 5 yrs= 19-5= 14 yrs.
HOPE IT HELPS.
Present age of X and Y are in the ratio 5:6 respectively. Seven years hence this ratio will become 6:7 respectively. Wat is X’s present age?- a)35
- b)42
- c)49
- d)Cannot be determined
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
Present age of X and Y are in the ratio 5:6 respectively. Seven years hence this ratio will become 6:7 respectively. Wat is X’s present age?
a)
35
b)
42
c)
49
d)
Cannot be determined
e)
None of these
|
|
Shivu D B answered |
Let
X present age is 5a---(1)
Y present age is 6a
After 7 years
5a+7/6a+7=6/7
cross multiply
So
7(5a+7)=6(6a+7)
35a+49=36a+42
a=7--(2)
substitute (2) in (1)
X present age is 5(7)= 35
X present age is 5a---(1)
Y present age is 6a
After 7 years
5a+7/6a+7=6/7
cross multiply
So
7(5a+7)=6(6a+7)
35a+49=36a+42
a=7--(2)
substitute (2) in (1)
X present age is 5(7)= 35
5 years ago the ratio of the age of A to that of B was 7 : 6. 20 years hence, the ratio of the age of A to that of B will be 22 : 21. What is the sum of their current ages?- a)30 years
- b)31.67 years
- c)33.33 years
- d)36 years
Correct answer is option 'B'. Can you explain this answer?
5 years ago the ratio of the age of A to that of B was 7 : 6. 20 years hence, the ratio of the age of A to that of B will be 22 : 21. What is the sum of their current ages?
a)
30 years
b)
31.67 years
c)
33.33 years
d)
36 years

|
EduRev SSC CGL answered |
Let the age of A 5 years ago = 7x
The age of B 5 years ago = 6x
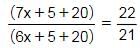
147x + 525 = 132x + 550
15x = 25

So the answer = (7x + 5 + 6x + 5) = 13x + 10
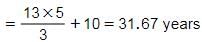
Hence, Option B is correct.
The age of B 5 years ago = 6x
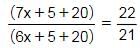
147x + 525 = 132x + 550
15x = 25

So the answer = (7x + 5 + 6x + 5) = 13x + 10
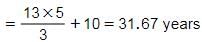
Hence, Option B is correct.
The average age of A, B, C and D is 20 years and their ages are in Arithmetic progression. If the youngest among them is 15 years old, what is the age of the oldest one?- a)15 years
- b)20 years
- c)21 years
- d)25 years
Correct answer is option 'D'. Can you explain this answer?
The average age of A, B, C and D is 20 years and their ages are in Arithmetic progression. If the youngest among them is 15 years old, what is the age of the oldest one?
a)
15 years
b)
20 years
c)
21 years
d)
25 years

|
G.K Academy answered |
Since their ages are in Arithmetic progression, the average age of the youngest and oldest must be 20 years.
15 + The age of the oldest one = 20 × 2
The age of the oldest one = 40 – 15 = 25 years
Hence, Option D is correct.
15 + The age of the oldest one = 20 × 2
The age of the oldest one = 40 – 15 = 25 years
Hence, Option D is correct.
The ratio of the ages of A, B and C is 2 : 3 : 5 respectively. The age of A is what percentage of the difference between the ages of B and C?- a)60
- b)75
- c)80
- d)100
Correct answer is option 'D'. Can you explain this answer?
The ratio of the ages of A, B and C is 2 : 3 : 5 respectively. The age of A is what percentage of the difference between the ages of B and C?
a)
60
b)
75
c)
80
d)
100
|
|
Ishaan Roy answered |
Understanding the Age Ratio
The ages of A, B, and C are in the ratio 2 : 3 : 5. This means we can represent their ages as:
- Age of A = 2x
- Age of B = 3x
- Age of C = 5x
Here, 'x' is a common multiplier for their ages.
Calculating the Difference Between Ages of B and C
To find the difference between the ages of B and C:
- Difference between ages of B and C = Age of C - Age of B
- Difference = 5x - 3x = 2x
Calculating Age of A as a Percentage of the Difference
Next, we need to find what percentage the age of A is of the difference calculated above:
- Age of A = 2x
- Difference = 2x
Now, we can calculate the percentage:
\[
\text{Percentage} = \left( \frac{\text{Age of A}}{\text{Difference}} \right) \times 100
\]
Substituting the values:
\[
\text{Percentage} = \left( \frac{2x}{2x} \right) \times 100 = 1 \times 100 = 100\%
\]
Conclusion
The age of A is 100% of the difference between the ages of B and C. Therefore, the correct answer is option 'D'.
This demonstrates how the ratio of their ages directly correlates to the percentage calculation based on the differences in their ages.
The ages of A, B, and C are in the ratio 2 : 3 : 5. This means we can represent their ages as:
- Age of A = 2x
- Age of B = 3x
- Age of C = 5x
Here, 'x' is a common multiplier for their ages.
Calculating the Difference Between Ages of B and C
To find the difference between the ages of B and C:
- Difference between ages of B and C = Age of C - Age of B
- Difference = 5x - 3x = 2x
Calculating Age of A as a Percentage of the Difference
Next, we need to find what percentage the age of A is of the difference calculated above:
- Age of A = 2x
- Difference = 2x
Now, we can calculate the percentage:
\[
\text{Percentage} = \left( \frac{\text{Age of A}}{\text{Difference}} \right) \times 100
\]
Substituting the values:
\[
\text{Percentage} = \left( \frac{2x}{2x} \right) \times 100 = 1 \times 100 = 100\%
\]
Conclusion
The age of A is 100% of the difference between the ages of B and C. Therefore, the correct answer is option 'D'.
This demonstrates how the ratio of their ages directly correlates to the percentage calculation based on the differences in their ages.
The ratio of the current age of A to that of B is 10 : 9. 16 years hence, the ratio of the age of A to that of B will be 13 : 12. What is the current age of B?- a)32 years
- b)36 years
- c)40 years
- d)48 years
Correct answer is option 'D'. Can you explain this answer?
The ratio of the current age of A to that of B is 10 : 9. 16 years hence, the ratio of the age of A to that of B will be 13 : 12. What is the current age of B?
a)
32 years
b)
36 years
c)
40 years
d)
48 years

|
Bayshore Academy answered |
Let the current age of A = 10x
The current age of B = 9x
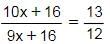
120x + 192 = 117x + 208
3x = 16

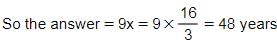
Hence, Option D is correct.
The current age of B = 9x
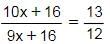
120x + 192 = 117x + 208
3x = 16

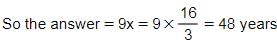
Hence, Option D is correct.
The ratio of the ages of A, B and C is 5 : 3 : 5 respectively. The age of A is what percentage of the combined age of B and C?- a)37.50
- b)40
- c)48
- d)62.50
Correct answer is option 'D'. Can you explain this answer?
The ratio of the ages of A, B and C is 5 : 3 : 5 respectively. The age of A is what percentage of the combined age of B and C?
a)
37.50
b)
40
c)
48
d)
62.50
|
|
Ishaan Roy answered |
Understanding the Age Ratio
The ages of A, B, and C are given in the ratio of 5:3:5. This means:
- A's age = 5x
- B's age = 3x
- C's age = 5x
Here, 'x' is a common multiplier.
Calculating the Combined Age of B and C
To find the combined age of B and C:
- B's age + C's age = 3x + 5x = 8x
Finding the Percentage of A's Age to B and C's Combined Age
Now, we need to find what percentage A's age is of the combined age of B and C:
- A's age = 5x
- Combined age of B and C = 8x
The percentage is calculated using the formula:
\[
\text{Percentage} = \left(\frac{\text{A's age}}{\text{Combined age of B and C}}\right) \times 100
\]
Substituting the values:
\[
\text{Percentage} = \left(\frac{5x}{8x}\right) \times 100
\]
The 'x' cancels out:
\[
\text{Percentage} = \left(\frac{5}{8}\right) \times 100 = 62.5\%
\]
Conclusion
Thus, the age of A is **62.50%** of the combined age of B and C. Therefore, the correct answer is option **D**.
The ages of A, B, and C are given in the ratio of 5:3:5. This means:
- A's age = 5x
- B's age = 3x
- C's age = 5x
Here, 'x' is a common multiplier.
Calculating the Combined Age of B and C
To find the combined age of B and C:
- B's age + C's age = 3x + 5x = 8x
Finding the Percentage of A's Age to B and C's Combined Age
Now, we need to find what percentage A's age is of the combined age of B and C:
- A's age = 5x
- Combined age of B and C = 8x
The percentage is calculated using the formula:
\[
\text{Percentage} = \left(\frac{\text{A's age}}{\text{Combined age of B and C}}\right) \times 100
\]
Substituting the values:
\[
\text{Percentage} = \left(\frac{5x}{8x}\right) \times 100
\]
The 'x' cancels out:
\[
\text{Percentage} = \left(\frac{5}{8}\right) \times 100 = 62.5\%
\]
Conclusion
Thus, the age of A is **62.50%** of the combined age of B and C. Therefore, the correct answer is option **D**.
If the age of Mohit is 250% more than the age of Jeenat and the sum of their ages is 54 years, what is the age of Jeenat?
- a)8 years
- b)10 years
- c)12 years
- d)16 years
Correct answer is option 'C'. Can you explain this answer?
If the age of Mohit is 250% more than the age of Jeenat and the sum of their ages is 54 years, what is the age of Jeenat?
a)
8 years
b)
10 years
c)
12 years
d)
16 years

|
Target Study Academy answered |
Ages → Jeenat : Mohit = 100 : (100 + 250) = 2 : 7
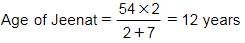
Hence, Option C is correct.
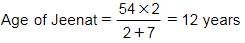
Hence, Option C is correct.
If the average age of A and B is 44 years and the ratio of the age of A to that of B is 5 : 6, what was the ratio of the age of A to that of B 16 years back?- a)1 : 2
- b)2 : 3
- c)3 : 4
- d)4 : 5
Correct answer is option 'C'. Can you explain this answer?
If the average age of A and B is 44 years and the ratio of the age of A to that of B is 5 : 6, what was the ratio of the age of A to that of B 16 years back?
a)
1 : 2
b)
2 : 3
c)
3 : 4
d)
4 : 5

|
Ssc Cgl answered |
Sum of the current ages = 44 × 2 = 88 years
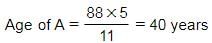
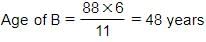
So the answer = 40 – 16 : 48 – 16 = 24 : 32 = 3 : 4
Hence, Option C is correct.
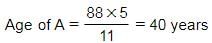
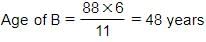
So the answer = 40 – 16 : 48 – 16 = 24 : 32 = 3 : 4
Hence, Option C is correct.
The age of Rohit is 25% more than the age of Sachin. If the sum of their ages is 45 years, what is the difference between their ages?
- a)2 years
- b)3 years
- c)4 years
- d)5 years
Correct answer is option 'D'. Can you explain this answer?
The age of Rohit is 25% more than the age of Sachin. If the sum of their ages is 45 years, what is the difference between their ages?
a)
2 years
b)
3 years
c)
4 years
d)
5 years

|
Target Study Academy answered |
The age of Sachin = 4x
The age of Rohit = 5x
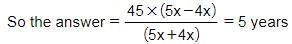
Hence, Option D is correct.
The age of Rohit = 5x
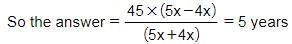
Hence, Option D is correct.
The ratio of the ages of A, B and C is 2 : 3 : 1 respectively. If the sum of their ages is 48 years, what is the age of C?- a)2 years
- b)4 years
- c)6 years
- d)8 years
Correct answer is option 'D'. Can you explain this answer?
The ratio of the ages of A, B and C is 2 : 3 : 1 respectively. If the sum of their ages is 48 years, what is the age of C?
a)
2 years
b)
4 years
c)
6 years
d)
8 years
|
|
Ishaan Roy answered |
Understanding the Problem
To find C's age given the ratio of A, B, and C's ages, we first need to break down the information provided.
Given Ratios
- The ratio of ages of A, B, and C is 2:3:1.
- This means if we let A's age be 2x, B's age be 3x, and C's age be x, where x is a common multiplier.
Sum of Ages
- The problem states that the sum of their ages is 48 years.
- Therefore, we can set up the equation:
- 2x + 3x + x = 48
Simplifying the Equation
- Combine the terms:
- 6x = 48
Solving for x
- Now, divide both sides by 6:
- x = 48 / 6
- x = 8
Finding Individual Ages
- Now that we have x, we can find the ages:
- A's age = 2x = 2 * 8 = 16 years
- B's age = 3x = 3 * 8 = 24 years
- C's age = x = 8 years
Conclusion
- Thus, the age of C is 8 years.
Therefore, the correct answer is option 'D'.
To find C's age given the ratio of A, B, and C's ages, we first need to break down the information provided.
Given Ratios
- The ratio of ages of A, B, and C is 2:3:1.
- This means if we let A's age be 2x, B's age be 3x, and C's age be x, where x is a common multiplier.
Sum of Ages
- The problem states that the sum of their ages is 48 years.
- Therefore, we can set up the equation:
- 2x + 3x + x = 48
Simplifying the Equation
- Combine the terms:
- 6x = 48
Solving for x
- Now, divide both sides by 6:
- x = 48 / 6
- x = 8
Finding Individual Ages
- Now that we have x, we can find the ages:
- A's age = 2x = 2 * 8 = 16 years
- B's age = 3x = 3 * 8 = 24 years
- C's age = x = 8 years
Conclusion
- Thus, the age of C is 8 years.
Therefore, the correct answer is option 'D'.
At present Tarun is twice the age of Vishal and half of Tanvi’s age. After four years Tarun will be 1.5 times Vishal’s age and Tanvi will be 2.5 times Vishal’s age. What is Tanvi’s present age?- a)12 years
- b)8 years
- c)20 years
- d)16 years
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
At present Tarun is twice the age of Vishal and half of Tanvi’s age. After four years Tarun will be 1.5 times Vishal’s age and Tanvi will be 2.5 times Vishal’s age. What is Tanvi’s present age?
a)
12 years
b)
8 years
c)
20 years
d)
16 years
e)
None of these

|
Kavya Sharma answered |
Vishal's present age = x years
Tarun's present age = 2x years
Tanvi's present age = 4x years
After 4 years.
Tarun's age = 1.5 * Vishal's age
=> 2x + 4 = 1.5(x+4)
=> 2x - 1.5x = 2
=>0.5x = 2 => x = 2/0.5 = 4
Tanvi's present age = 16 years.
The difference between the ages of two persons is 10 years. Fifteen years ago, the elder one was twice as old as the younger one. The present age of elder person is?- a)25 years
- b)35 years
- c)45 years
- d)55 years
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The difference between the ages of two persons is 10 years. Fifteen years ago, the elder one was twice as old as the younger one. The present age of elder person is?
a)
25 years
b)
35 years
c)
45 years
d)
55 years
e)
None of these

|
Aishwarya Rajput answered |
Let the elder person be 'A' and younger be 'B'. A - B = 10. A = 10 +B. 15 years ago,A -15 = 2(B-15) 10 + B - 15 = 2(B - 15). B -5 = 2B - 30. B = 25 A = B + 10 Therefore, A = 35
The average age of Manan, Shaket and Dileep is 48 years. If the ratio of the age of Manan to that of Shaket to that of Dileep is 6 : 7 : 5, what is the difference between the ages of Manan and Dileep?- a)4 years
- b)5 years
- c)6 years
- d)8 years
Correct answer is option 'D'. Can you explain this answer?
The average age of Manan, Shaket and Dileep is 48 years. If the ratio of the age of Manan to that of Shaket to that of Dileep is 6 : 7 : 5, what is the difference between the ages of Manan and Dileep?
a)
4 years
b)
5 years
c)
6 years
d)
8 years

|
EduRev SSC CGL answered |
Sum of their ages = 48 × 3 = 144 years

Hence, Option D is correct.

Hence, Option D is correct.
If the age of Rahul is 60% more than the age of Ajay and the sum of their ages is 91 years, what is the difference between their ages?- a)15 years
- b)16 years
- c)18 years
- d)21 years
Correct answer is option 'D'. Can you explain this answer?
If the age of Rahul is 60% more than the age of Ajay and the sum of their ages is 91 years, what is the difference between their ages?
a)
15 years
b)
16 years
c)
18 years
d)
21 years

|
G.K Academy answered |
Ages → Ajay : Rahul = 100 : (100 + 60) = 5 : 8
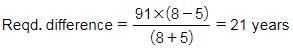
Hence, Option D is correct.
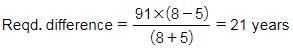
Hence, Option D is correct.
80% of the current age of Vishal is 50% of the current age of Shivam. If the average age of Shivam and Vishal is 39 years, what is the current age of Vishal?- a)30 years
- b)32 years
- c)36 years
- d)40 years
Correct answer is option 'A'. Can you explain this answer?
80% of the current age of Vishal is 50% of the current age of Shivam. If the average age of Shivam and Vishal is 39 years, what is the current age of Vishal?
a)
30 years
b)
32 years
c)
36 years
d)
40 years

|
Malavika Rane answered |
Given Information:
- 80% of Vishal's current age = 50% of Shivam's current age
- Average age of Shivam and Vishal = 39 years
Let's solve the problem step by step:
Step 1: Express the Given Information Mathematically
Let V be the current age of Vishal and S be the current age of Shivam.
- 0.8V = 0.5S (80% of Vishal's age is equal to 50% of Shivam's age)
- (V + S) / 2 = 39 (Average age of Shivam and Vishal is 39)
Step 2: Solve the Equations
From the first equation, we can express S in terms of V:
0.8V = 0.5S
S = 1.6V
Substitute S = 1.6V into the second equation:
(V + 1.6V) / 2 = 39
2.6V / 2 = 39
1.3V = 39
V = 39 / 1.3
V = 30
Step 3: Determine Vishal's Current Age
Therefore, Vishal's current age is 30 years.
Conclusion:
The current age of Vishal is 30 years. Hence, option A (30 years) is the correct answer.
The ratio of the current age of A to that of B is 8 : 5. 14 years hence, the ratio of the age of A to that of B will be 5 : 4. What is the difference between their ages?- a)2 years
- b)4 years
- c)6 years
- d)8 years
Correct answer is option 'C'. Can you explain this answer?
The ratio of the current age of A to that of B is 8 : 5. 14 years hence, the ratio of the age of A to that of B will be 5 : 4. What is the difference between their ages?
a)
2 years
b)
4 years
c)
6 years
d)
8 years

|
Ssc Cgl answered |
Let the current age of A = 8x
The current age of B = 5x
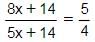
32x + 56 = 25x + 70
7x = 14
x = 2
Reqd. difference = (8x – 5x) = 3x = 3 × 2 = 6 years
Hence, Option C is correct.
The current age of B = 5x
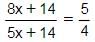
32x + 56 = 25x + 70
7x = 14
x = 2
Reqd. difference = (8x – 5x) = 3x = 3 × 2 = 6 years
Hence, Option C is correct.
The ages of A, B and C are ‘X’ years, ‘X + 50’ years and ‘X – 20’ years respectively, if the average age of all three is 40 years, what is the value of X?- a)20
- b)25
- c)30
- d)33.33
Correct answer is option 'C'. Can you explain this answer?
The ages of A, B and C are ‘X’ years, ‘X + 50’ years and ‘X – 20’ years respectively, if the average age of all three is 40 years, what is the value of X?
a)
20
b)
25
c)
30
d)
33.33

|
Target Study Academy answered |
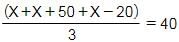
3X + 30 = 120
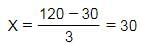
Hence, Option C is correct.
If the ages (in years) of A, B and C are different prime numbers between 40 and 50, what is the age of the second oldest among the three?- a)41 years
- b)43 years
- c)47 years
- d)49 years
Correct answer is option 'B'. Can you explain this answer?
If the ages (in years) of A, B and C are different prime numbers between 40 and 50, what is the age of the second oldest among the three?
a)
41 years
b)
43 years
c)
47 years
d)
49 years

|
EduRev SSC CGL answered |
Prime numbers between 40 and 50 = 41, 43 and 47
So the age of the second oldest among the three = 43 years
Hence, Option B is correct.
So the age of the second oldest among the three = 43 years
Hence, Option B is correct.
Chapter doubts & questions for Age - Quantitative Aptitude for Competitive Examinations 2025 is part of Bank Exams exam preparation. The chapters have been prepared according to the Bank Exams exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Bank Exams 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Age - Quantitative Aptitude for Competitive Examinations in English & Hindi are available as part of Bank Exams exam.
Download more important topics, notes, lectures and mock test series for Bank Exams Exam by signing up for free.
Quantitative Aptitude for Competitive Examinations
166 videos|137 docs|171 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup