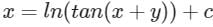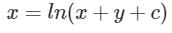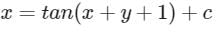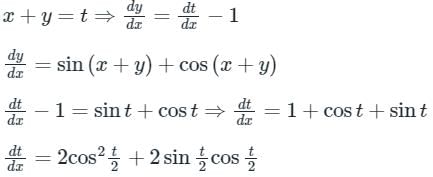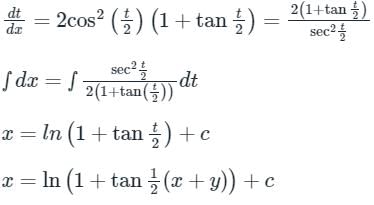All Exams >
Civil Engineering (CE) >
Engineering Mathematics for Civil Engineering >
All Questions
All questions of Partial Differential Equations for Civil Engineering (CE) Exam
Consider the following differential equation: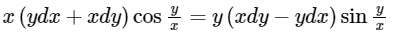
Which of the following is the solution of the above equation (c is an arbitrary constant)?- a)
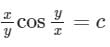
- b)
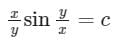
- c)
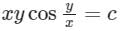
- d)
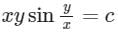
Correct answer is option 'C'. Can you explain this answer?
Consider the following differential equation:
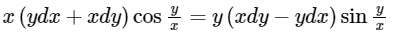
Which of the following is the solution of the above equation (c is an arbitrary constant)?
a)
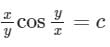
b)
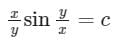
c)
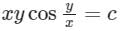
d)
|
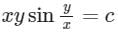
Sanya Agarwal answered |
Given differential eqaution is,
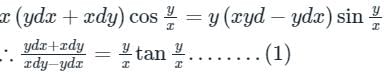
Let, y = v × x
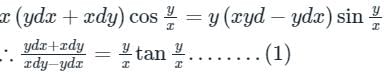
Let, y = v × x
dy = vdx + xdv
By substituting values of Y and dY in equation 1, we get
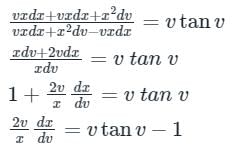
Integrating both sides
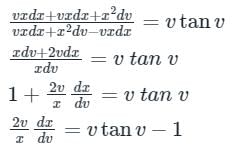
Integrating both sides
2 log x = log |sec v| - log v + log c
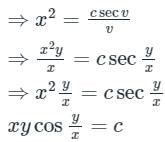
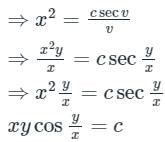
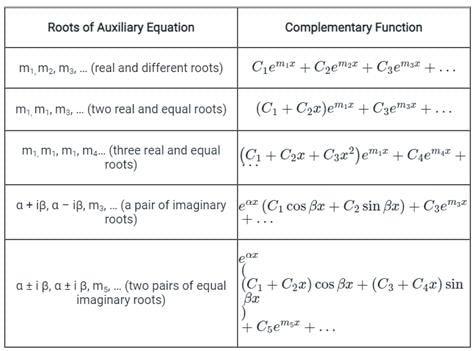
The differential equation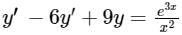
is solving by the method of variation of parameters, where the complementary function is given by- y = c1y1(x) + c2y2(x)- a)The value of y1(x) = e3x
- b)The value of y2(x) = e3x
- c)The value of y2(x) = xe3x
- d)
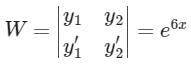
Correct answer is option 'D'. Can you explain this answer?
The differential equation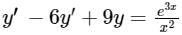is solving by the method of variation of parameters, where the complementary function is given by- y = c1y1(x) + c2y2(x)
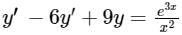is solving by the method of variation of parameters, where the complementary function is given by- y = c1y1(x) + c2y2(x)a)
The value of y1(x) = e3x
b)
The value of y2(x) = e3x
c)
The value of y2(x) = xe3x
d)
|
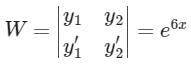
Engineers Adda answered |
Concept:
Calculation:
Calculation:
Given:
(D2 – 6D + 9)y = e3x/x2
Auxiliary equation is
(D2 – 6D + 9) = 0
⇒ (D – 3)2 = 0
C.F. = (C1 + C2x) e3x
C.F = C1(e3x) + C2(xe3x)
Solution of differential equation (D2 + 4)y = cosec 2x- a)
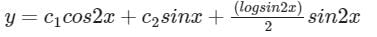
- b)
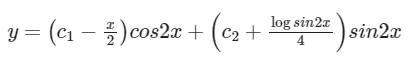
- c)
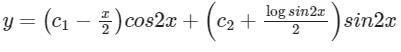
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Solution of differential equation (D2 + 4)y = cosec 2x
a)
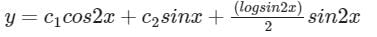
b)
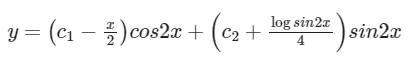
c)
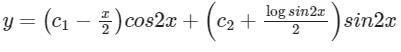
d)
None of these
|
|
Engineers Adda answered |
Auxiliary equation:
m2 + 4 = 0
m = ±2i
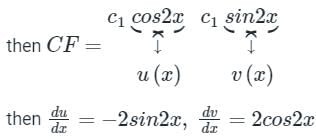
By wrongskion,
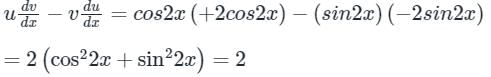
PI = A u(x) + B v(x)
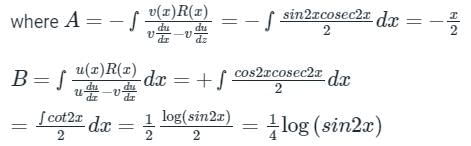
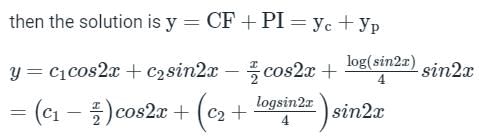
Let \(f\left( x \right) = \;\left\{ {\begin{array}{*{20}{c}} { - π }&{if\;}&{ - π
be a periodic function of period 2π. The coefficient of sin 5x in the Fourier series expansion of f(x) in the interval [-π, π] is- a)4/5
- b)5/4
- c)4/3
- d)3/4
Correct answer is option 'A'. Can you explain this answer?
Let \(f\left( x \right) = \;\left\{ {\begin{array}{*{20}{c}} { - π }&{if\;}&{ - π
be a periodic function of period 2π. The coefficient of sin 5x in the Fourier series expansion of f(x) in the interval [-π, π] is
be a periodic function of period 2π. The coefficient of sin 5x in the Fourier series expansion of f(x) in the interval [-π, π] is
a)
4/5
b)
5/4
c)
4/3
d)
3/4
|
|
Sanvi Kapoor answered |
Concept:
Let f(x) is a periodic function defined in (C, C + 2L) with period 2L, then the Fourier series of f(x) is
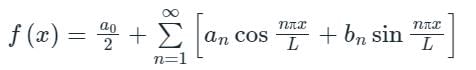
Where the Fourier series coefficients a0, an, and bn are given by
Let f(x) is a periodic function defined in (C, C + 2L) with period 2L, then the Fourier series of f(x) is
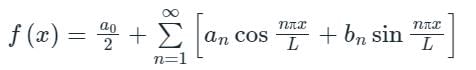
Where the Fourier series coefficients a0, an, and bn are given by
- If f(x) is an odd function, then only bn exists where a0 and bn are zero.
- If f(x) is an even function, then both a0 and an exists where bn is zero.
Calculation:
\(f\left( x \right) = \;\left\{ {\begin{array}{*{20}{c}} { - π }&{if\;}&{ - π
Fundamental period = 2π
The given function is an odd function and hence only bn exists.
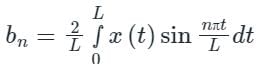
Here L = 2π
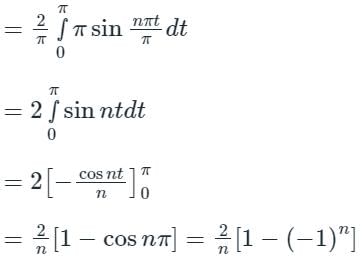
Now, the Fourier series of f(x) is,
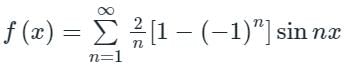
The coefficient of sin 5x = b5
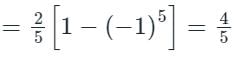
\(f\left( x \right) = \;\left\{ {\begin{array}{*{20}{c}} { - π }&{if\;}&{ - π
Fundamental period = 2π
The given function is an odd function and hence only bn exists.
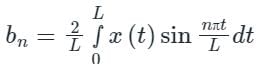
Here L = 2π
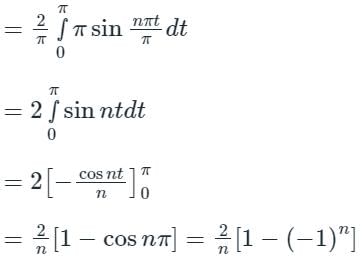
Now, the Fourier series of f(x) is,
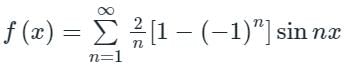
The coefficient of sin 5x = b5
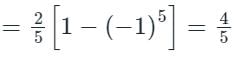
The following partial differential equation is defined for u:u (x, y)
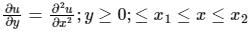
The set auxiliary conditions necessary to solve the equation uniquely, is - a)three initial conditions
- b)three boundary conditions
- c)two initial conditions and one boundary condition
- d)one initial conditions and two boundary conditions
Correct answer is option 'D'. Can you explain this answer?
The following partial differential equation is defined for u:u (x, y)
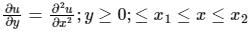
The set auxiliary conditions necessary to solve the equation uniquely, is
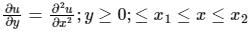
The set auxiliary conditions necessary to solve the equation uniquely, is
a)
three initial conditions
b)
three boundary conditions
c)
two initial conditions and one boundary condition
d)
one initial conditions and two boundary conditions
|
Pioneer Academy answered |
Given:
∵ y ≥ 0 ⇒ It can be replaced with ‘t’.
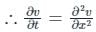
This is a 1-D Heat equation. It measures temperature distribution in a uniform rod.
The general solution is u = f(x, t)
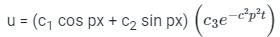
Auxiliary solutions include both initial and boundary conditions.
(1) Number of initial conditions = Highest order of time derivative in partial differential = 1
(2) The number of boundary conditions:
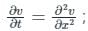To solve this partial differential equation, it needs to be integrated twice that will introduce two arbitrary constants.
Hence 2 boundary conditions and 1 initial condition are required to solve this Partial differential equation.
∵ y ≥ 0 ⇒ It can be replaced with ‘t’.
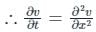
This is a 1-D Heat equation. It measures temperature distribution in a uniform rod.
The general solution is u = f(x, t)
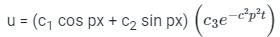
Auxiliary solutions include both initial and boundary conditions.
(1) Number of initial conditions = Highest order of time derivative in partial differential = 1
(2) The number of boundary conditions:
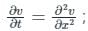To solve this partial differential equation, it needs to be integrated twice that will introduce two arbitrary constants.Hence 2 boundary conditions and 1 initial condition are required to solve this Partial differential equation.
The Fourier series expansion of x3 in the interval −1 ≤ x < 1 with periodic continuation has- a)only sine terms
- b)only cosine terms
- c)both sine and cosine terms
- d)only sine terms and a non-zero constant
Correct answer is option 'A'. Can you explain this answer?
The Fourier series expansion of x3 in the interval −1 ≤ x < 1 with periodic continuation has
a)
only sine terms
b)
only cosine terms
c)
both sine and cosine terms
d)
only sine terms and a non-zero constant
|
|
Sanya Agarwal answered |
f(x) = x3
find f(x) is even or odd
put x = -x
f(-x) = - x3
f(x) = -f(-x) hence it is odd function
for odd function, ao = an = 0
Fourier Series for odd function has only bn term
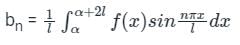
Hence only sine terms are left in Fourier expansion of x3
Additional Information
Fourier Series
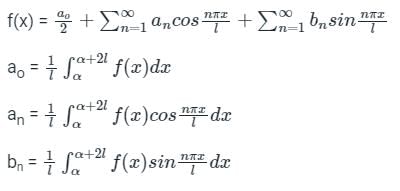
find f(x) is even or odd
put x = -x
f(-x) = - x3
f(x) = -f(-x) hence it is odd function
for odd function, ao = an = 0
Fourier Series for odd function has only bn term
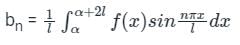
Hence only sine terms are left in Fourier expansion of x3
Additional Information
Fourier Series
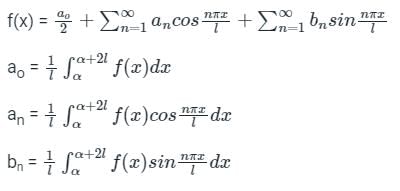
What are the conditions called which are required for a signal to fulfil to be represented as Fourier series?- a)Dirichlet’s conditions
- b)Gibbs phenomenon
- c)Fourier conditions
- d)Fourier phenomenon
Correct answer is option 'A'. Can you explain this answer?
What are the conditions called which are required for a signal to fulfil to be represented as Fourier series?
a)
Dirichlet’s conditions
b)
Gibbs phenomenon
c)
Fourier conditions
d)
Fourier phenomenon
|
|
Sanya Agarwal answered |
When the Dirichlet’s conditions are satisfied, then only for a signal, the fourier series exist. Fourier series is of two types- trigonometric series and exponential series.
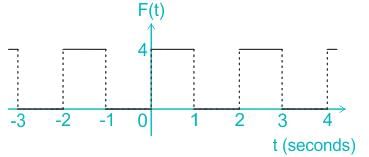
F(t) is a periodic square wave function as shown. It takes only two values, 4 and 0, and stays at each of these values for 1 second before changing. What is the constant term in the Fourier series expansion of F(t)?
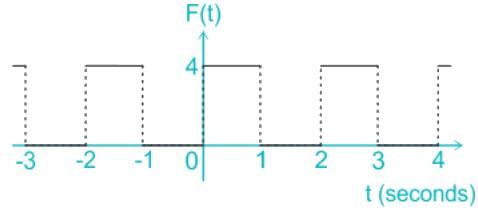
- a)1
- b)2
- c)3
- d)4
Correct answer is option 'B'. Can you explain this answer?
F(t) is a periodic square wave function as shown. It takes only two values, 4 and 0, and stays at each of these values for 1 second before changing. What is the constant term in the Fourier series expansion of F(t)?
a)
1
b)
2
c)
3
d)
4
|
|
Pioneer Academy answered |
Concept:
Fourier Series is defined as
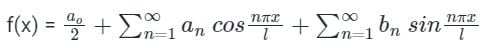
Calculation:
Given:
f(t) is an even periodic function, Since
f(-t) = f(t)
The constant term in the Fourier series is: ao/2
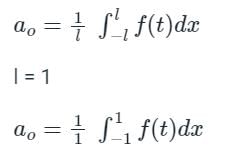
Since the function is not continious, we need to break the integral according to interval
from -1 to 0, f(t) = 0,
from 0 to 1, f(t) = 4
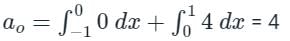
The constant term is:
a0/2 = 4/2 = 2
Mistake Points
Avoid using the integral property of even function because the given function f(t) is not continuous. Though the function given is an even periodic function but it is not continuous
Fourier Series is defined as
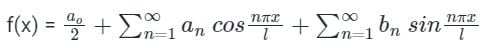
Calculation:
Given:
f(t) is an even periodic function, Since
f(-t) = f(t)
The constant term in the Fourier series is: ao/2
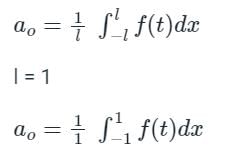
Since the function is not continious, we need to break the integral according to interval
from -1 to 0, f(t) = 0,
from 0 to 1, f(t) = 4
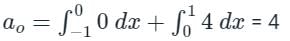
The constant term is:
a0/2 = 4/2 = 2
Mistake Points
Avoid using the integral property of even function because the given function f(t) is not continuous. Though the function given is an even periodic function but it is not continuous
Find the particular solution of the differential equation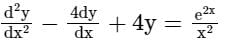
- a)
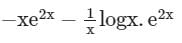
- b)
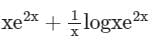
- c)
- d)
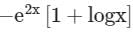
Correct answer is option 'D'. Can you explain this answer?
Find the particular solution of the differential equation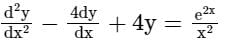
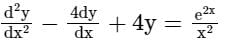
a)
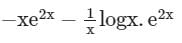
b)
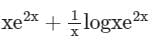
c)
d)
|
|
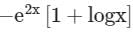
Engineers Adda answered |
Given differential equation is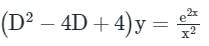
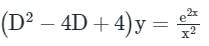
auxiliary equation is (D − 2)2 = 0 ⇒ D = 2, 2
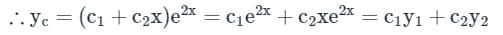
This problem can be solved by using the method of variation of parameters. Then
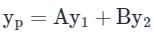
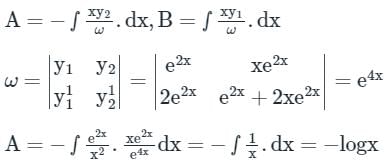
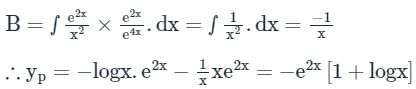
Choose the condition from below that is not a part of Dirichlet’s conditions?- a)If it is continuous then there are a finite number of discontinuities in the period T1
- b)It has a finite average value over the period T
- c)It has a finite number of positive and negative maxima in the period T
- d)It is a periodic signal
Correct answer is option 'D'. Can you explain this answer?
Choose the condition from below that is not a part of Dirichlet’s conditions?
a)
If it is continuous then there are a finite number of discontinuities in the period T1
b)
It has a finite average value over the period T
c)
It has a finite number of positive and negative maxima in the period T
d)
It is a periodic signal
|
Madhurima Banerjee answered |
The condition that is not a part of Dirichlet is:
- The condition that the function is harmonic on the boundary.
- The condition that the function is harmonic on the boundary.
The function f(x, y) satisfies the Laplace equation
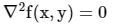
on a circular domain of radius r = 1 with its center at point P with coordinates x = 0, y = 0. The value of this function on the circular boundary of this domain is equal to 3.
The numerical value of f(0, 0) is:- a)0
- b)2
- c)3
- d)1
Correct answer is option 'C'. Can you explain this answer?
The function f(x, y) satisfies the Laplace equation
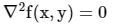
on a circular domain of radius r = 1 with its center at point P with coordinates x = 0, y = 0. The value of this function on the circular boundary of this domain is equal to 3.
The numerical value of f(0, 0) is:
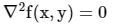
on a circular domain of radius r = 1 with its center at point P with coordinates x = 0, y = 0. The value of this function on the circular boundary of this domain is equal to 3.
The numerical value of f(0, 0) is:
a)
0
b)
2
c)
3
d)
1
|
|
Pioneer Academy answered |
Given that,
The function f(x, y) satisfies the Laplace equation ∇2f(x, y) = 0
on a circular domain of radius r = 1 with its center at point P with coordinates x = 0, y = 0.
The value of this function on the circular boundary of this domain is equal to 3.
Here it is given that the value of the function is 3 for its domain, which signifies that it is a constant function whose value is 3.
So the value of the function at (0, 0) is 3.
The function f(x, y) satisfies the Laplace equation ∇2f(x, y) = 0
on a circular domain of radius r = 1 with its center at point P with coordinates x = 0, y = 0.
The value of this function on the circular boundary of this domain is equal to 3.
Here it is given that the value of the function is 3 for its domain, which signifies that it is a constant function whose value is 3.
So the value of the function at (0, 0) is 3.
What is Fourier series?- a)The representation of periodic signals in a mathematical manner is called a Fourier series
- b)The representation of non periodic signals in a mathematical manner is called a Fourier series
- c)The representation of non periodic signals in terms of complex exponentials or sinusoids is called a Fourier series
- d)The representation of periodic signals in terms of complex exponentials or sinusoids is called a Fourier series
Correct answer is option 'D'. Can you explain this answer?
What is Fourier series?
a)
The representation of periodic signals in a mathematical manner is called a Fourier series
b)
The representation of non periodic signals in a mathematical manner is called a Fourier series
c)
The representation of non periodic signals in terms of complex exponentials or sinusoids is called a Fourier series
d)
The representation of periodic signals in terms of complex exponentials or sinusoids is called a Fourier series
|
|
Sanvi Kapoor answered |
The Fourier series is the representation of non periodic signals in terms of complex exponentials, or equivalently in terms of sine and cosine waveform leads to Fourier series. In other words, Fourier series is a mathematical tool that allows representation of any periodic wave as a sum of harmonically related sinusoids.
If we use the Fourier transform 
to solve the partial differential equation 
in the half-plane {(x, y) : -∞ < x < ∞, 0 < y < ∞} the Fourier modes ϕk(y) depend on y as yα and yβ. The values of α and β are - a)
- b)
- c)
- d)
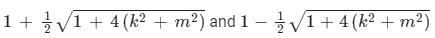
Correct answer is option 'C'. Can you explain this answer?
If we use the Fourier transform to solve the partial differential equation in the half-plane {(x, y) : -∞ < x < ∞, 0 < y < ∞} the Fourier modes ϕk(y) depend on y as yα and yβ. The values of α and β are
to solve the partial differential equation in the half-plane {(x, y) : -∞ < x < ∞, 0 < y < ∞} the Fourier modes ϕk(y) depend on y as yα and yβ. The values of α and β are a)
b)
c)
d)
|
|
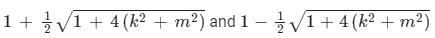
Sanvi Kapoor answered |
The Fourier transform,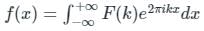 
CALCULATION:
We have;
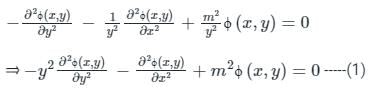
Now take the derivative of ϕ(x, y) we have;
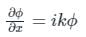
Again derivative we have;
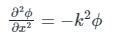
Now putting these values in equation 1) we have;
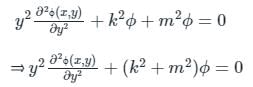
Now, by applying Cauchy's differential equation we have;
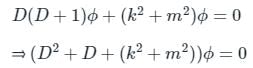
Again solving we have;
The roots are written as;
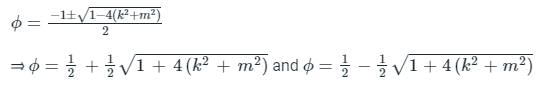
Hence option 3) is the correct answer.
CALCULATION:
We have;
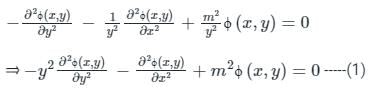
Now take the derivative of ϕ(x, y) we have;
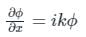
Again derivative we have;
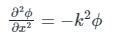
Now putting these values in equation 1) we have;
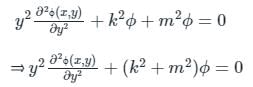
Now, by applying Cauchy's differential equation we have;
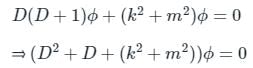
Again solving we have;
The roots are written as;
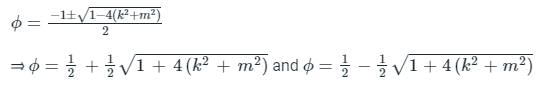
Hence option 3) is the correct answer.
The differential equation
is solving by the method of variation of parameters, the Wronskian will be______- a)-2
- b)-4
- c)4
- d)-8
Correct answer is option 'A'. Can you explain this answer?
The differential equation is solving by the method of variation of parameters, the Wronskian will be______
is solving by the method of variation of parameters, the Wronskian will be______a)
-2
b)
-4
c)
4
d)
-8
|
|
Sanya Agarwal answered |
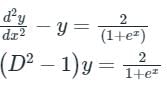
Auxiliary equation, D2 – 1 = 0
⇒ D = ± 1
C.F. = C1ex + C2e−x
Here, y1 = ex
y2 = e-x
y1′ = ex
y2′ = −e−x
y2′ = −e−x
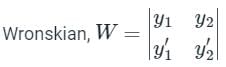
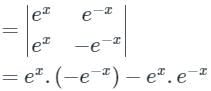
= -1 - 1 = -2
The differential equation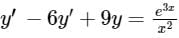
is solving by the method of variation of parameters, then Wronskian will be –Wronskian for solution y = c1y1(t) + c2y2(t) is defined as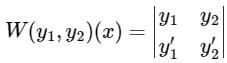
- a)e3x
- b)e6x
- c)e9x
- d)e-3x
Correct answer is option 'B'. Can you explain this answer?
The differential equation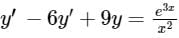is solving by the method of variation of parameters, then Wronskian will be –
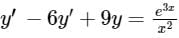is solving by the method of variation of parameters, then Wronskian will be –Wronskian for solution y = c1y1(t) + c2y2(t) is defined as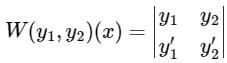
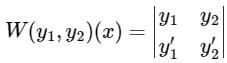
a)
e3x
b)
e6x
c)
e9x
d)
e-3x
|
|
Sanya Agarwal answered |
Give equation is (D2 – 6D + 9)y = e3x/x2
Auxiliary equation is, (D2 – 6D + 9) = 0
⇒ (D – 3)2 = 0
C.F. = (C1 + C2x) e3x
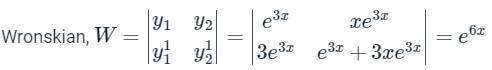
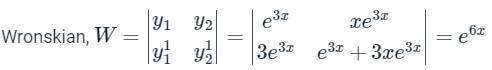
Solve (x2 – y2) dx – xydy = 0- a)x2(x2 + 2y2) = constant
- b)x2(x2 + 3y2) = constant
- c)x2(x2 - 2y2) = constant
- d)x2(2x2 - 2y2) = constant
Correct answer is option 'C'. Can you explain this answer?
Solve (x2 – y2) dx – xydy = 0
a)
x2(x2 + 2y2) = constant
b)
x2(x2 + 3y2) = constant
c)
x2(x2 - 2y2) = constant
d)
x2(2x2 - 2y2) = constant
|
|
Sanya Agarwal answered |
(x2 – y2) dx – xydy = 0
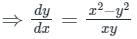
This homogeneous in x & y
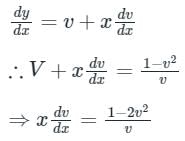
Separating the variables
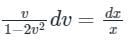
Integrating on both side
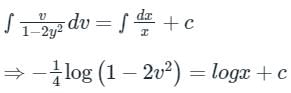
⇒ 4logx + log(1 − 2v2) = −4c
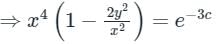
⇒ x2 (x2 – 2y2) = constant
The Wronskian of the differential equation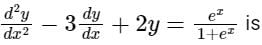
- a)ex
- b)-e3x
- c)e2x
- d)e5x
Correct answer is option 'B'. Can you explain this answer?
The Wronskian of the differential equation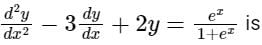
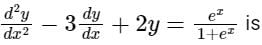
a)
ex
b)
-e3x
c)
e2x
d)
e5x
|
|
Engineers Adda answered |
If the given differential equation is in the form, y'' + py' + qy = x
Where, p, q, x are functions of x.
Then Wronskian is,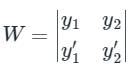
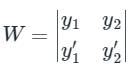
Here, y1 and y2 are the solutions of y'' + py' + qy = 0
Given differential equation is,
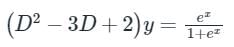
Auxiliary equation is,
D2 – 3D + 2 = 0
⇒ D = 1, 2
C.F. = c1 e2x + c2 ex
y1 = e2x, y2 = ex
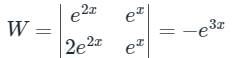
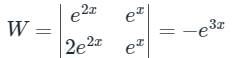
Solutions of Laplace’s equation, which are continuous through the second derivatives are called- a)Bessel functions
- b)odd functions
- c)harmonic functions
- d)fundamental functions
Correct answer is option 'C'. Can you explain this answer?
Solutions of Laplace’s equation, which are continuous through the second derivatives are called
a)
Bessel functions
b)
odd functions
c)
harmonic functions
d)
fundamental functions
|
|
Sanya Agarwal answered |
Solutions of Laplace’s equation having continuous second-order partial derivatives is given by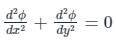 
and it is called a harmonic function (where Φ = any constant).
E.g. Φ = 2xy satisfies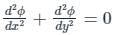
hence it is called a harmonic function.
Conjugate of Harmonic function:
If f(z) = u + iv is an analytic function then imaginary part v is known as conjugate harmonic functions of u (But the converse is not true) and u is conjugate harmonic of (-v).
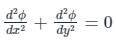and it is called a harmonic function (where Φ = any constant).E.g. Φ = 2xy satisfies
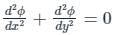hence it is called a harmonic function.Conjugate of Harmonic function:
If f(z) = u + iv is an analytic function then imaginary part v is known as conjugate harmonic functions of u (But the converse is not true) and u is conjugate harmonic of (-v).
Consider the differential equation given below:
The integrating factor of the differential equation is:- a)(1 - x2)-1/4
- b)(1 - x2)-1/2
- c)(1 - x2)-3/4
- d)(1 - x2)-3/2
Correct answer is option 'A'. Can you explain this answer?
Consider the differential equation given below:
The integrating factor of the differential equation is:
The integrating factor of the differential equation is:
a)
(1 - x2)-1/4
b)
(1 - x2)-1/2
c)
(1 - x2)-3/4
d)
(1 - x2)-3/2
|
|
Sanya Agarwal answered |
The solution of a linear differential equation of a general form shown above is:
y(I.F) = ∫Q(x) (IF) dx + C
Where:
IF = Integrating factor calculated as:
I.F = e∫Pdx
Calculation:
Given:
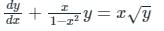
The above differential equation is not in a general form. Converting it first in the general form of a linear differential equation, we divide the equation by √y to get:
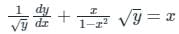
Let √y = u
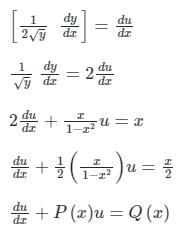
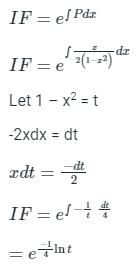
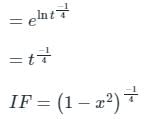
The value of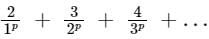 
will be- a)P > 0
- b)P > 1
- c)P > 2
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
The value of 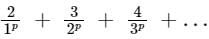will be
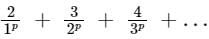will bea)
P > 0
b)
P > 1
c)
P > 2
d)
None of these
|
|
Sanya Agarwal answered |
Concept:
Consider the infinite series ∑un = u1 + u2 + u3 + … ∞
Consider the infinite series ∑un = u1 + u2 + u3 + … ∞
- Convergence test:
- If un tends to a finite or unique limit as n → ∞, the series is said to be convergent.
- If un tends to ± ∞ as n → ∞, the series is said to be divergent.
- If un does not tend to a unique limit as n → ∞, the series is said to be oscillatory or non-convergent.
Calculation:
Given series is
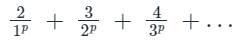
nth term of series is given by
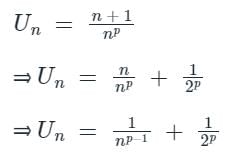
Un will provide definite and unique value if
p - 1 > 1
⇒ p > 2
Given series is
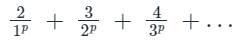
nth term of series is given by
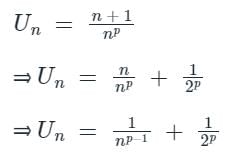
Un will provide definite and unique value if
p - 1 > 1
⇒ p > 2
Which one of the following is a Dirichlet condition?- a)
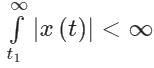
- b)Signal x(t) must have a finite number of maxima and minima in the expansion interval
- c)x(t) can have an infinite number of finite discontinuities in the expansion interval
- d)x2(t) must be absolutely summable
Correct answer is option 'B'. Can you explain this answer?
Which one of the following is a Dirichlet condition?
a)
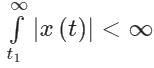
b)
Signal x(t) must have a finite number of maxima and minima in the expansion interval
c)
x(t) can have an infinite number of finite discontinuities in the expansion interval
d)
x2(t) must be absolutely summable
|
|
Sanvi Kapoor answered |
Dirichlet Conditions in Fourier Transformation are as follows:
- f(x) must absolutely integrable over a period, i.e.,
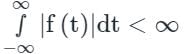
- f(x) must have a finite number of extrema in any given interval, i.e. there must be a finite number of maxima and minima in the interval.
- f(x) must have a finite number of discontinues in any given interval, however, the discontinuity cannot be infinite.
- f(x) must be bounded.
F(t) is a periodic square wave function as shown. It takes only two values, 4 and 0, and stays at each of these values for 1 second before changing. What is the constant term in the Fourier series expansion of F(t)?
- a)1
- b)2
- c)3
- d)4
Correct answer is option 'B'. Can you explain this answer?
F(t) is a periodic square wave function as shown. It takes only two values, 4 and 0, and stays at each of these values for 1 second before changing. What is the constant term in the Fourier series expansion of F(t)?
a)
1
b)
2
c)
3
d)
4
|
|
Sanvi Kapoor answered |
Fourier Series is defined as
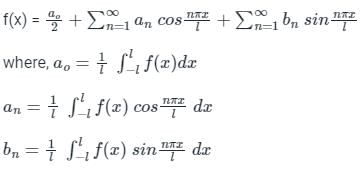
Calculation:
Given:
f(t) is an even periodic function, Since
f(-t) = f(t)
The constant term in the Fourier series is: ao/2
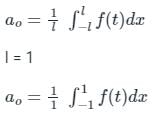
Since the function is not continious, we need to break the integral according to interval
from -1 to 0, f(t) = 0,
from 0 to 1, f(t) = 4
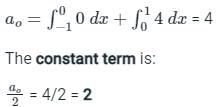
Mistake Points
Avoid using the integral property of even function because the given function f(t) is not continuous. Though the function given is an even periodic function but it is not continuous
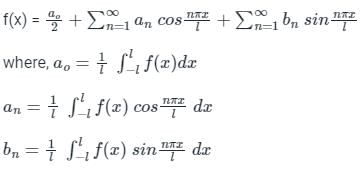
Calculation:
Given:
f(t) is an even periodic function, Since
f(-t) = f(t)
The constant term in the Fourier series is: ao/2
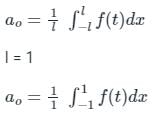
Since the function is not continious, we need to break the integral according to interval
from -1 to 0, f(t) = 0,
from 0 to 1, f(t) = 4
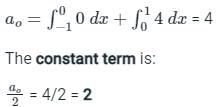
Mistake Points
Avoid using the integral property of even function because the given function f(t) is not continuous. Though the function given is an even periodic function but it is not continuous
The Fourier series expansion of x3 in the interval −1 ≤ x < 1 with periodic continuation has- a)only sine terms
- b)only cosine terms
- c)both sine and cosine terms
- d)only sine terms and a non-zero constant
Correct answer is option 'A'. Can you explain this answer?
The Fourier series expansion of x3 in the interval −1 ≤ x < 1 with periodic continuation has
a)
only sine terms
b)
only cosine terms
c)
both sine and cosine terms
d)
only sine terms and a non-zero constant
|
|
Sanvi Kapoor answered |
f(x) = x3
find f(x) is even or odd
put x = -x
f(-x) = - x3
f(x) = -f(-x) hence it is odd function
for odd function, ao = an = 0
Fourier Series for odd function has only bn term
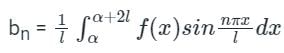
Hence only sine terms are left in Fourier expansion of x3
Additional Information
Fourier Series
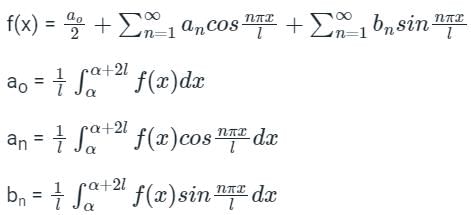
find f(x) is even or odd
put x = -x
f(-x) = - x3
f(x) = -f(-x) hence it is odd function
for odd function, ao = an = 0
Fourier Series for odd function has only bn term
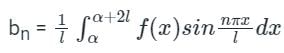
Hence only sine terms are left in Fourier expansion of x3
Additional Information
Fourier Series
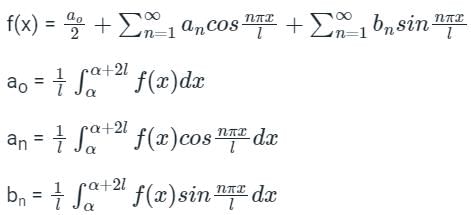
Let x(t) be a periodic signal with time period T, Let y(t) = x(t – to) + x(t + to) for some to. The fourier series coefficients of y(t) are denoted by bk. If bk = 0 for all odd K. Then to can be equal to- a)T/8
- b)T/4
- c)T/2
- d)2T
Correct answer is option 'B'. Can you explain this answer?
Let x(t) be a periodic signal with time period T, Let y(t) = x(t – to) + x(t + to) for some to. The fourier series coefficients of y(t) are denoted by bk. If bk = 0 for all odd K. Then to can be equal to
a)
T/8
b)
T/4
c)
T/2
d)
2T
|
|
Naina Das answered |
Understanding the Problem
The signal y(t) is defined as y(t) = x(t - to) + x(t + to). The Fourier series coefficients of y(t) are denoted by bk, and it is given that bk = 0 for all odd k. This means that y(t) only contains even harmonics.
Significance of bk = 0 for Odd k
- A signal with only even harmonics is symmetric with respect to time.
- This symmetry indicates that y(t) must exhibit an even function property, which is a key condition for having only even Fourier coefficients.
Time Shifts and Periodicity
- The periodic signal x(t) has a period T.
- The shifts of to in y(t) affect the symmetry of the signal.
Determining the Value of to
- The crucial point is that for y(t) to maintain the even symmetry, the shifts (to) must relate to the period T.
- Analyzing the conditions, we find that if to = T/4, then the shifts will ensure that x(t) appears symmetrically around t=0.
Verification of Option B (T/4)
- If to = T/4:
- Then y(t) = x(t - T/4) + x(t + T/4).
- This results in a symmetric configuration around t = 0, ensuring that the contributions to the Fourier coefficients from odd k cancel out.
Concluding the Explanation
- Therefore, the only value of to that maintains the even symmetry in the Fourier series representation of y(t) is T/4.
- This confirms that the correct answer is option 'B'.
This understanding not only illustrates the relationship between periodic signals and their Fourier series but also highlights the importance of symmetry in signal analysis.
The signal y(t) is defined as y(t) = x(t - to) + x(t + to). The Fourier series coefficients of y(t) are denoted by bk, and it is given that bk = 0 for all odd k. This means that y(t) only contains even harmonics.
Significance of bk = 0 for Odd k
- A signal with only even harmonics is symmetric with respect to time.
- This symmetry indicates that y(t) must exhibit an even function property, which is a key condition for having only even Fourier coefficients.
Time Shifts and Periodicity
- The periodic signal x(t) has a period T.
- The shifts of to in y(t) affect the symmetry of the signal.
Determining the Value of to
- The crucial point is that for y(t) to maintain the even symmetry, the shifts (to) must relate to the period T.
- Analyzing the conditions, we find that if to = T/4, then the shifts will ensure that x(t) appears symmetrically around t=0.
Verification of Option B (T/4)
- If to = T/4:
- Then y(t) = x(t - T/4) + x(t + T/4).
- This results in a symmetric configuration around t = 0, ensuring that the contributions to the Fourier coefficients from odd k cancel out.
Concluding the Explanation
- Therefore, the only value of to that maintains the even symmetry in the Fourier series representation of y(t) is T/4.
- This confirms that the correct answer is option 'B'.
This understanding not only illustrates the relationship between periodic signals and their Fourier series but also highlights the importance of symmetry in signal analysis.
If ψ = 2x2y - xz3, then the Laplacian of ψ is- a)4yz - 6xz
- b)4z - 6xy
- c)4y - 6xz
- d)2xy - 6yz
Correct answer is option 'C'. Can you explain this answer?
If ψ = 2x2y - xz3, then the Laplacian of ψ is
a)
4yz - 6xz
b)
4z - 6xy
c)
4y - 6xz
d)
2xy - 6yz
|
|
Sanya Agarwal answered |
Laplacian operator in the Cartesian system is:
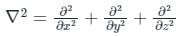
Laplacian operator in Cylindrical system is:
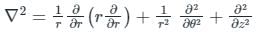
Laplacian operator in Spherical system is:
Calculation:
The Laplacian of a scalar field ψ = 2x2y - xz3
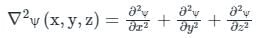
Solving the above we will get option 3 as the correct answer.
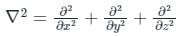
Laplacian operator in Cylindrical system is:
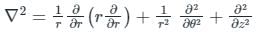
Laplacian operator in Spherical system is:
Calculation:
The Laplacian of a scalar field ψ = 2x2y - xz3
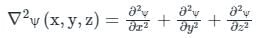
Solving the above we will get option 3 as the correct answer.
Who discovered Fourier series?- a)Jean Baptiste de Fourier
- b)Jean Baptiste Joseph Fourier
- c)Fourier Joseph
- d)Jean Fourier
Correct answer is option 'B'. Can you explain this answer?
Who discovered Fourier series?
a)
Jean Baptiste de Fourier
b)
Jean Baptiste Joseph Fourier
c)
Fourier Joseph
d)
Jean Fourier
|
|
Sanvi Kapoor answered |
The Fourier series is the representation of non periodic signals in terms of complex exponentials or sine or cosine waveform. This was discovered by Jean Baptiste Joseph Fourier in 18th century.
The Fourier series expansion of x3 in the interval −1 ≤ x < 1 with periodic continuation has- a)only sine terms
- b)only cosine terms
- c)both sine and cosine terms
- d)only sine terms and a non-zero constant
Correct answer is option 'A'. Can you explain this answer?
The Fourier series expansion of x3 in the interval −1 ≤ x < 1 with periodic continuation has
a)
only sine terms
b)
only cosine terms
c)
both sine and cosine terms
d)
only sine terms and a non-zero constant
|
|
Sanvi Kapoor answered |
f(x) = x3
find f(x) is even or odd
put x = -x
f(-x) = - x3
f(x) = -f(-x) hence it is odd function
for odd function, ao = an = 0
Fourier Series for odd function has only bn term
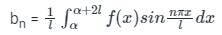
Hence only sine terms are left in Fourier expansion of x3
Additional Information
Fourier Series
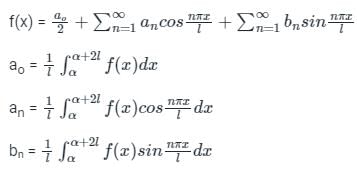
find f(x) is even or odd
put x = -x
f(-x) = - x3
f(x) = -f(-x) hence it is odd function
for odd function, ao = an = 0
Fourier Series for odd function has only bn term
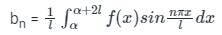
Hence only sine terms are left in Fourier expansion of x3
Additional Information
Fourier Series
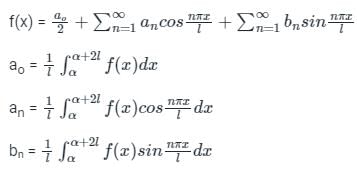
The function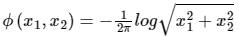 
is the solution of- a)Heat equation
- b)Transport equation
- c)Laplace equation
- d)Wave equation
Correct answer is option 'C'. Can you explain this answer?
The function 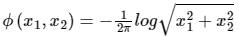is the solution of
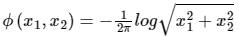is the solution ofa)
Heat equation
b)
Transport equation
c)
Laplace equation
d)
Wave equation
|
|
Sanya Agarwal answered |
If a function ϕ(x1, x2) satisfies the Laplace equation,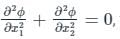 
then the function is the solution of the Laplace equation.
Calculation:
Given function is,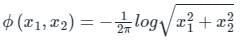
Differentiating ϕ partially with respect to x1
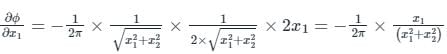
Again differentiating ϕ partially with respect to x1
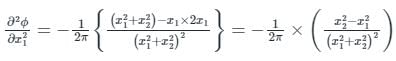
Similarly, differentiating ϕ partially with respect to x2 twice, we will get,
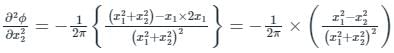
Adding above two equations,
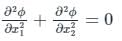
As the given function satisfies the Laplace equation ∇2ϕ = 0, hence it is the solution of Laplace equation.
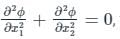then the function is the solution of the Laplace equation.Calculation:
Given function is,
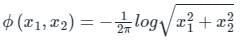
Differentiating ϕ partially with respect to x1
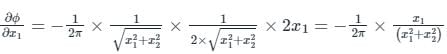
Again differentiating ϕ partially with respect to x1
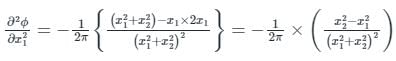
Similarly, differentiating ϕ partially with respect to x2 twice, we will get,
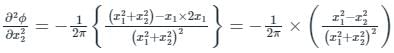
Adding above two equations,
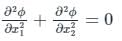
As the given function satisfies the Laplace equation ∇2ϕ = 0, hence it is the solution of Laplace equation.
Consider the differential equation given below:
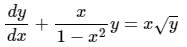
The integrating factor of the differential equation is:- a)(1 - x2)-1/4
- b)(1 - x2)-1/2
- c)(1 - x2)-3/4
- d)(1 - x2)-3/2
Correct answer is option 'A'. Can you explain this answer?
Consider the differential equation given below:
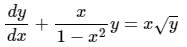
The integrating factor of the differential equation is:
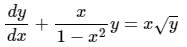
The integrating factor of the differential equation is:
a)
(1 - x2)-1/4
b)
(1 - x2)-1/2
c)
(1 - x2)-3/4
d)
(1 - x2)-3/2
|
|
Sanya Agarwal answered |
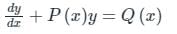
The solution of a linear differential equation of a general form shown above is:
y(I.F) = ∫Q(x) (IF) dx + C
Where:
IF = Integrating factor calculated as:
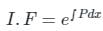
Calculation:
Given:
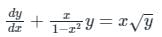
The above differential equation is not in a general form. Converting it first in the general form of a linear differential equation, we divide the equation by √y to get:
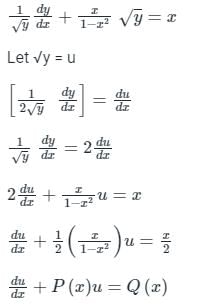
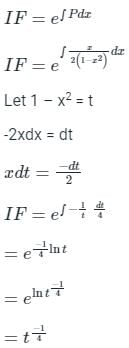
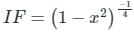
Let g: [0,∞) → [0,∞) be a function defined by g(x) = x – [x], where [x] represents the integer part of x. (i.e., it is the largest integer which is less than or equal to x). The value of the constant term in the Fourier series expansion of g(x) is- a)0.5
- b)1
- c)2
- d)4
Correct answer is option 'A'. Can you explain this answer?
Let g: [0,∞) → [0,∞) be a function defined by g(x) = x – [x], where [x] represents the integer part of x. (i.e., it is the largest integer which is less than or equal to x). The value of the constant term in the Fourier series expansion of g(x) is
a)
0.5
b)
1
c)
2
d)
4
|
Mira Sharma answered |
Understanding the Function g(x)
The function g(x) = x - [x] represents the fractional part of x. It takes any non-negative real number and returns the decimal part. For example:
Periodicity of g(x)
The function g(x) is periodic with a period of 1, meaning:
Fourier Series Expansion
The Fourier series expansion of a periodic function can be expressed as:
Where a0 is the average value of the function over one period.
Calculating a0
To find the constant term a0 for g(x):
Conclusion
The value of the constant term in the Fourier series expansion of g(x) is therefore:
The function g(x) = x - [x] represents the fractional part of x. It takes any non-negative real number and returns the decimal part. For example:
- g(2.3) = 2.3 - 2 = 0.3
- g(5.7) = 5.7 - 5 = 0.7
- g(3.0) = 3.0 - 3 = 0.0
Periodicity of g(x)
The function g(x) is periodic with a period of 1, meaning:
- g(x + 1) = g(x)
- g(x) has the same behavior in each interval [n, n+1) for n = 0, 1, 2, ...
Fourier Series Expansion
The Fourier series expansion of a periodic function can be expressed as:
- f(x) = a0/2 + Σ(an * cos(nωx) + bn * sin(nωx))
Where a0 is the average value of the function over one period.
Calculating a0
To find the constant term a0 for g(x):
- Calculate the average over one period (0 to 1):
- a0 = (1 / T) * ∫ from 0 to T g(x) dx, where T = 1.
- Thus, a0 = ∫ from 0 to 1 (x) dx = [x^2 / 2] from 0 to 1 = 0.5.
Conclusion
The value of the constant term in the Fourier series expansion of g(x) is therefore:
- 0.5, which corresponds to option A.
The Laplace transform of e i5t where i = √−1, is- a)
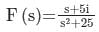
- b)
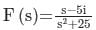
- c)
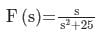
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
The Laplace transform of e i5t where i = √−1, is
a)
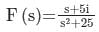
b)
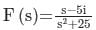
c)
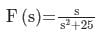
d)
None of these
|
|
Sanya Agarwal answered |
From the basic definition of Laplace transform:
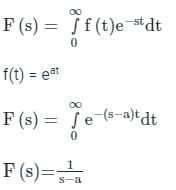
Calculation:
Given:
a = 5i
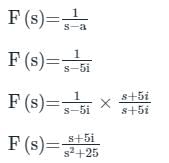
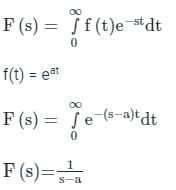
Calculation:
Given:
a = 5i
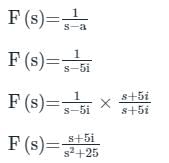
The serie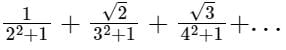s 
is-- a)Convergent
- b)Divergent
- c)Oscillatory
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
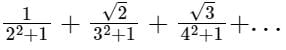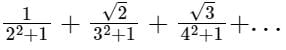The series is-
is-a)
Convergent
b)
Divergent
c)
Oscillatory
d)
None of these
|
|
Sanvi Kapoor answered |
Concept:
If the given is infinite series, find the partial sum (i.e. sum of first nth term )
If the sequence of partial sums is a convergent sequence (i.e. its limit exists and is finite) then the series is also called convergent
Calculations:
Consider the given series is
The nth term of the series is an =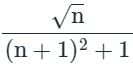
Given is infinite series, find the partial sum (i.e. sum of first nth term)
If the sequence of partial sums is a convergent sequence (i.e. its limit exists and is finite) then the series is also called convergent
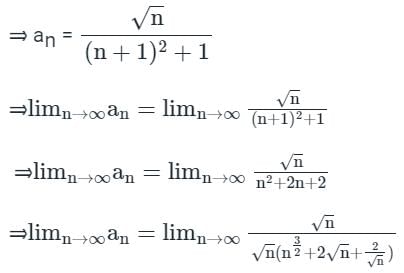
⇒ limn → ∞an = 0, limit exists and is finite
The series
is convergent.
If the given is infinite series, find the partial sum (i.e. sum of first nth term )
If the sequence of partial sums is a convergent sequence (i.e. its limit exists and is finite) then the series is also called convergent
Calculations:
Consider the given series is
The nth term of the series is an =
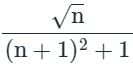
Given is infinite series, find the partial sum (i.e. sum of first nth term)
If the sequence of partial sums is a convergent sequence (i.e. its limit exists and is finite) then the series is also called convergent
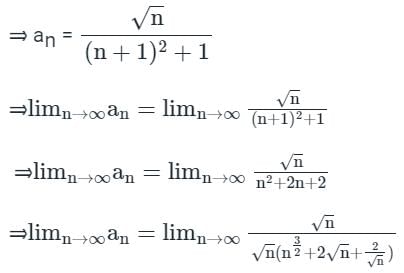
⇒ limn → ∞an = 0, limit exists and is finite
The series
is convergent.Consider the differential equation given below:
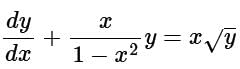
The integrating factor of the differential equation is:- a)(1 - x2)-1/4
- b)(1 - x2)-1/2
- c)(1 - x2)-3/4
- d)(1 - x2)-3/2
Correct answer is option 'A'. Can you explain this answer?
Consider the differential equation given below:
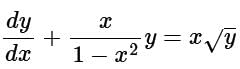
The integrating factor of the differential equation is:
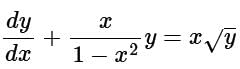
The integrating factor of the differential equation is:
a)
(1 - x2)-1/4
b)
(1 - x2)-1/2
c)
(1 - x2)-3/4
d)
(1 - x2)-3/2
|
|
Engineers Adda answered |
Concept:
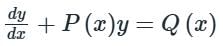
The solution of a linear differential equation of a general form shown above is:
y(I.F) = ∫Q(x) (IF) dx + C
Where:
IF = Integrating factor calculated as:
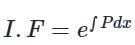
Calculation:
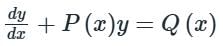
The solution of a linear differential equation of a general form shown above is:
y(I.F) = ∫Q(x) (IF) dx + C
Where:
IF = Integrating factor calculated as:
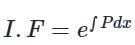
Calculation:
Given:
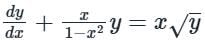
The above differential equation is not in a general form. Converting it first in the general form of a linear differential equation, we divide the equation by √y to get:
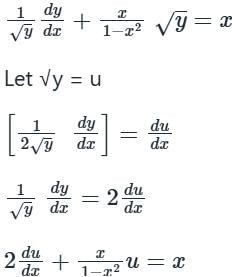
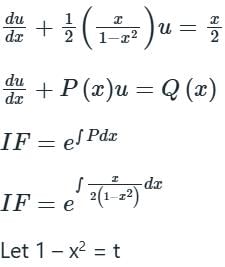
-2xdx = dt
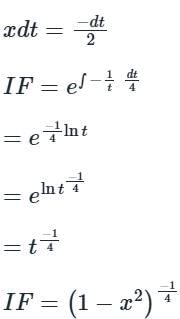
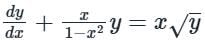
The above differential equation is not in a general form. Converting it first in the general form of a linear differential equation, we divide the equation by √y to get:
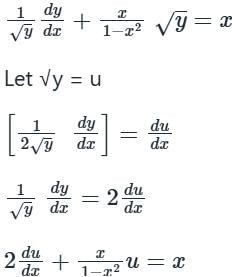
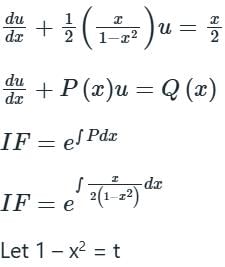
-2xdx = dt
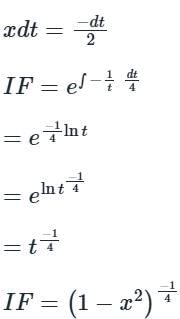
The solution of the differential equation
- a)-xe0.5x
- b)xe0.5x + xe-0.5x
- c)xe0.5x - xe-0.5x
- d)xe0.5x
Correct answer is option 'D'. Can you explain this answer?
The solution of the differential equation
a)
-xe0.5x
b)
xe0.5x + xe-0.5x
c)
xe0.5x - xe-0.5x
d)
xe0.5x
|
|
Sanya Agarwal answered |
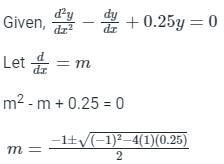
m = 0.5, 0.5
The solution is:
y = (C1 + C2x)e0.5x
For y = 0 at x = 0
0 = (C1 + C2(0))e0.5(0)
0 = C1
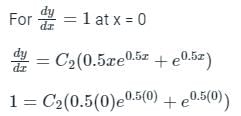
C2 = 1
y = (0 + (1)x)e0.5x
y = xe0.5x
The Fourier series expansion of the saw-toothed waveform f(x) = x in (- π, π) of period 2π gives the series,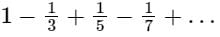 
The sum is equal to- a)π/2
- b)π2/4
- c)π2/16
- d)π/4
Correct answer is option 'D'. Can you explain this answer?
The Fourier series expansion of the saw-toothed waveform f(x) = x in (- π, π) of period 2π gives the series,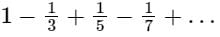
The sum is equal to
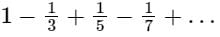
The sum is equal to
a)
π/2
b)
π2/4
c)
π2/16
d)
π/4
|
|
Sanvi Kapoor answered |
Concept:
If f(x) is periodic function of period ‘’T’’ then f(x) can be expressed as below:
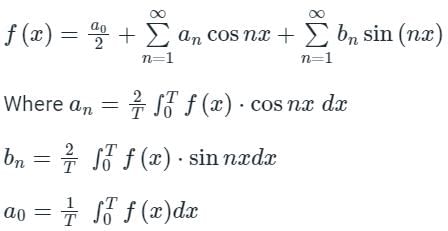
If f(x) is odd function, then only the coefficients of sin nx exists (i.e. an = 0 & a0 = 0).
Calculation:
We are given f(x) = x for x ∈ (-π, π)
sin a f(x) = x is odd So, an = 0, a0 = 0
So, now we have to find bn,
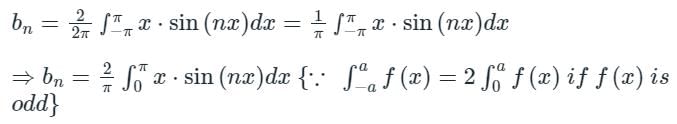
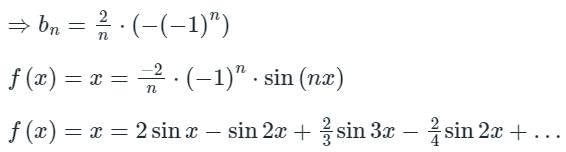
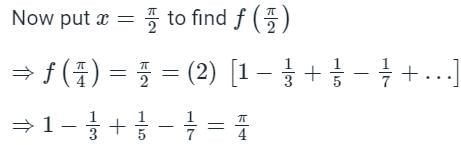
Hence required sum of series is
Alternate Method:
Taylor expansion of tan-1x is expressed in below:
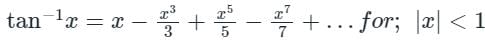
Put x = 9, above expansion series
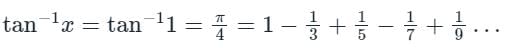
Hence π/4 is required sum of series.
If f(x) is periodic function of period ‘’T’’ then f(x) can be expressed as below:
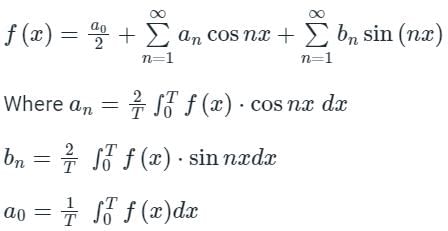
If f(x) is odd function, then only the coefficients of sin nx exists (i.e. an = 0 & a0 = 0).
Calculation:
We are given f(x) = x for x ∈ (-π, π)
sin a f(x) = x is odd So, an = 0, a0 = 0
So, now we have to find bn,
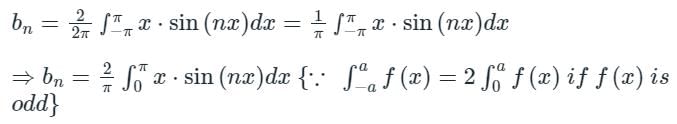
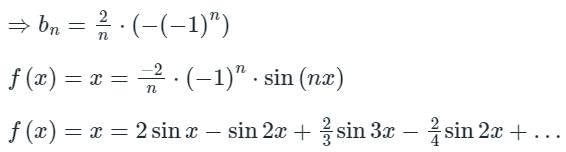
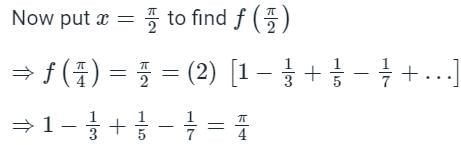
Hence required sum of series is
Alternate Method:
Taylor expansion of tan-1x is expressed in below:
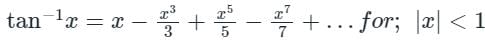
Put x = 9, above expansion series
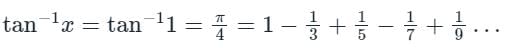
Hence π/4 is required sum of series.
Consider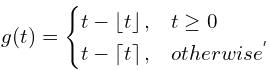 
where t ∈ R. Here [t] represents the largest integer less than or equal to t and [t] denotes the samllest integer greater than or equal to t. The coefficient of the second harmonic component of the fourier series representing g(t) is- a)1
- b)0
- c)-1
- d)2
Correct answer is option 'B'. Can you explain this answer?
Consider 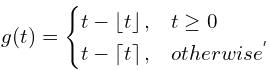where t ∈ R. Here [t] represents the largest integer less than or equal to t and [t] denotes the samllest integer greater than or equal to t. The coefficient of the second harmonic component of the fourier series representing g(t) is
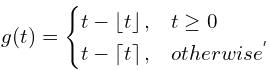where t ∈ R. Here [t] represents the largest integer less than or equal to t and [t] denotes the samllest integer greater than or equal to t. The coefficient of the second harmonic component of the fourier series representing g(t) isa)
1
b)
0
c)
-1
d)
2
|
Pammi Jaiswal answered |
Here [t] denotes, greatest integer function.
so , for positive t and negative t consider.
if t greater value equal to zero.
t -t value equal to 0.
t+t value equal to 0.according to given questions.
so , for positive t and negative t consider.
if t greater value equal to zero.
t -t value equal to 0.
t+t value equal to 0.according to given questions.
Given integral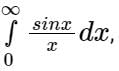 
Then the integral- a)Is not convergent
- b)Converges
- c)Converges absolutely
- d)Converges but not absolutely
Correct answer is option 'C'. Can you explain this answer?
Given integral 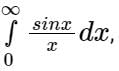Then the integral
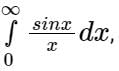Then the integrala)
Is not convergent
b)
Converges
c)
Converges absolutely
d)
Converges but not absolutely
|
|
Sanya Agarwal answered |
Concept:
Improper Integral: If a function f on [a, b] have infinite value then it is called is improper integral
Improper Integral: If a function f on [a, b] have infinite value then it is called is improper integral
- Improper Integral of the First kind:
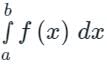is said to be the improper integral of the first kind if a = -∞ or b = ∞ or both. - Improper Integral of the second kind:
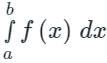is said to be the improper integral of the second kind if a or b is finite but f(x) is infinite for some x ∈ [a, b].
If the integration of the improper integral exists, then it is called as Converges, But if the limit of integration fails to exist, then the improper integral is said to be Diverge.
Calculation:
Given:
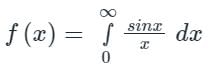
By using the Leibniz rule
Let, a is any parameter then,
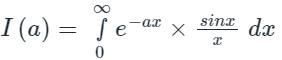...(1)
Differentiating w.r.t.a
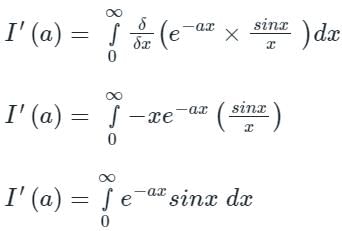
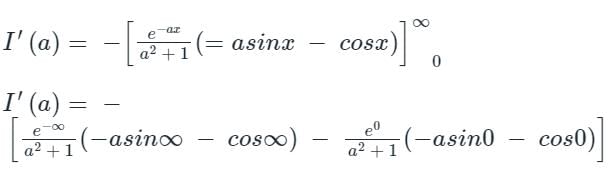
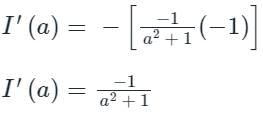
Integrating both side w.r.t a
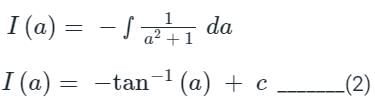
put x = ∞ in both (1) and (2)
From equation (1),
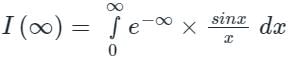
I(∞) = 0
From equation (2),
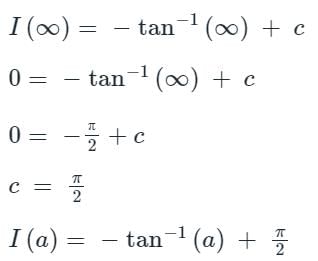
put a = 0, we get
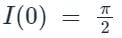
Therefore we can conclude that,
Hence,It is improper integral but having finite value so, It is Converges in [0, ∞].
Calculation:
Given:
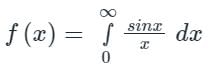
By using the Leibniz rule
Let, a is any parameter then,
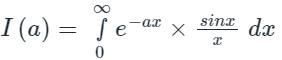...(1)Differentiating w.r.t.a
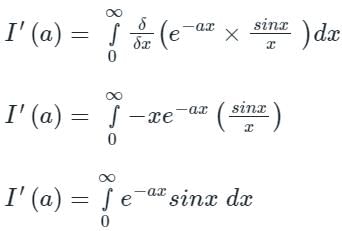
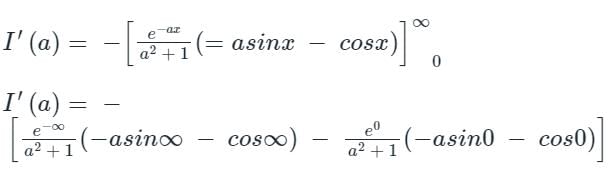
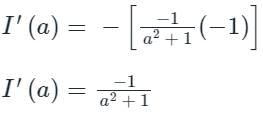
Integrating both side w.r.t a
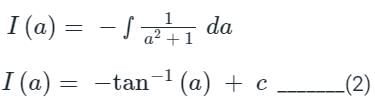
put x = ∞ in both (1) and (2)
From equation (1),
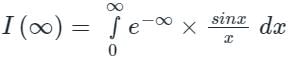
I(∞) = 0
From equation (2),
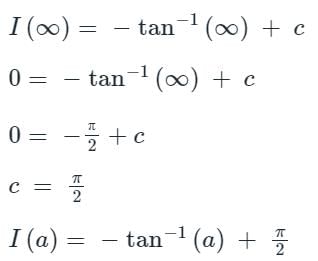
put a = 0, we get
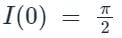
Therefore we can conclude that,
Hence,It is improper integral but having finite value so, It is Converges in [0, ∞].
The Fourier series is given by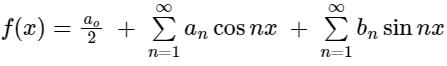 
in the interval -π < x < π.
Which among the following is true?- a)If f(x) = xcosx, the value of a0 = 0
- b)If f(x) = xcosx, the value of an = 0
- c)If f(x) = xsinx, the value of an = 0
- d)If f(x) = xsinx, the value of bn = 0
Correct answer is option 'D'. Can you explain this answer?
The Fourier series is given by 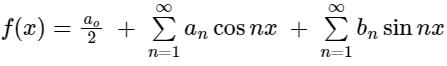in the interval -π < x < π.
Which among the following is true?
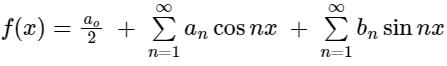in the interval -π < x < π. Which among the following is true?
a)
If f(x) = xcosx, the value of a0 = 0
b)
If f(x) = xcosx, the value of an = 0
c)
If f(x) = xsinx, the value of an = 0
d)
If f(x) = xsinx, the value of bn = 0
|
|
Sanya Agarwal answered |
Concept:
Fourier series:
The Fourier series for the function f(x) in the interval α < x < α + 2π is given by:
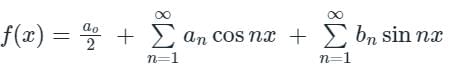
where
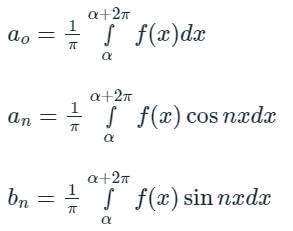
Even and odd function:
Calculation:
Given:
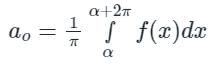
For f(x) = xcosx
f(x) is an odd function
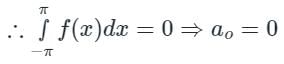[Option 1 is correct].
For f(x) = xcosx is an odd function whereas cosnx is an even function.
The product of odd and even function is an odd function.
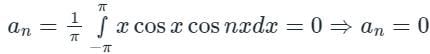[Option 2 is correct].
For f(x) = xsinx is an even function whereas cosnx is an even function.
The product of two even function is an even function.
[Option 3 is incorrect].
For f(x) = xsinx is an even function whereas sinnx is an odd function.
The product of even and odd function is an odd function.
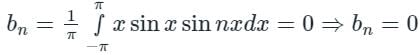[Option 4 is correct].
Fourier series:
The Fourier series for the function f(x) in the interval α < x < α + 2π is given by:
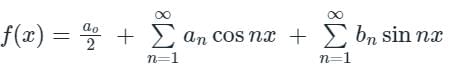
where
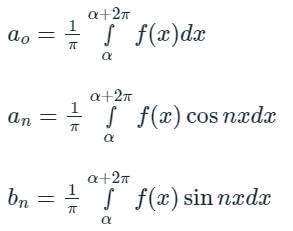
Even and odd function:
Calculation:
Given:
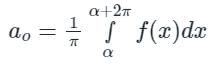
For f(x) = xcosx
f(x) is an odd function
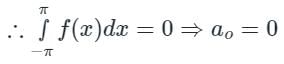[Option 1 is correct].For f(x) = xcosx is an odd function whereas cosnx is an even function.
The product of odd and even function is an odd function.
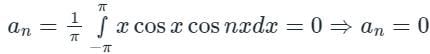[Option 2 is correct].For f(x) = xsinx is an even function whereas cosnx is an even function.
The product of two even function is an even function.
[Option 3 is incorrect].For f(x) = xsinx is an even function whereas sinnx is an odd function.
The product of even and odd function is an odd function.
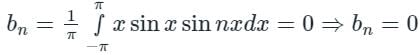[Option 4 is correct].Chapter doubts & questions for Partial Differential Equations - Engineering Mathematics for Civil Engineering 2025 is part of Civil Engineering (CE) exam preparation. The chapters have been prepared according to the Civil Engineering (CE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Civil Engineering (CE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Partial Differential Equations - Engineering Mathematics for Civil Engineering in English & Hindi are available as part of Civil Engineering (CE) exam.
Download more important topics, notes, lectures and mock test series for Civil Engineering (CE) Exam by signing up for free.
Engineering Mathematics for Civil Engineering
62 videos|105 docs|59 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup