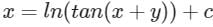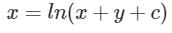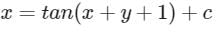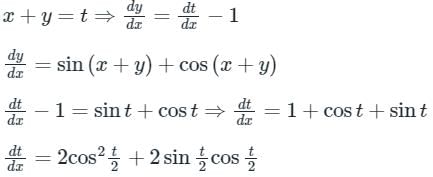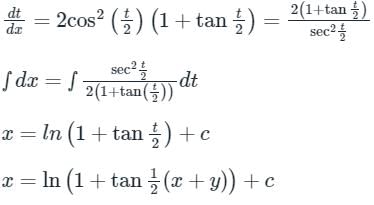All Exams >
Mechanical Engineering >
Engineering Mathematics for Mechanical Engineering >
All Questions
All questions of Differential Equations for Mechanical Engineering Exam
over the triangle is 
The following differential equation has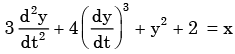 
a)degree = 2, order = 1b)degree = 1, order = 2 c)degree = 4, order = 3 d)degree = 2, order = 3Correct answer is option 'B'. Can you explain this answer?
|
Anmol Basu answered |
Order of highest derivative = 2
Hence, most appropriate answer is (b)
Hence, most appropriate answer is (b)
with the condition that y = 1 at x = 1, is
The general solution of the differential equation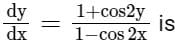
- a)tan y − cot x = c(c is a constant
- b)tan x − cot y = c(c is a constant)
- c)tan y + cot x = c(c is a constant)
- d)tan x + cot Y = c(c is a constant)
Correct answer is option 'C'. Can you explain this answer?
The general solution of the differential equation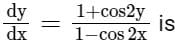
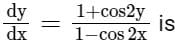
a)
tan y − cot x = c(c is a constant
b)
tan x − cot y = c(c is a constant)
c)
tan y + cot x = c(c is a constant)
d)
tan x + cot Y = c(c is a constant)
|
Pioneer Academy answered |
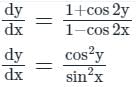
sec2ydy = cosec2x.dx
tan y = −cot x + c
tan y + cot x = c
A function n(x) satisfies the differential equation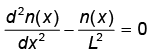 
where L is a constant. The boundary conditions are: n(0)=K and n(∞)= 0. The solution to this equation is - a)n(x) = K exp(x/L)
- b)n(x) = K exp( x / √L )
- c)n(x) = K2 exp(-x/L)
- d)n(x) = K exp( -x/L)
Correct answer is option 'D'. Can you explain this answer?
A function n(x) satisfies the differential equation 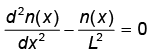where L is a constant. The boundary conditions are: n(0)=K and n(∞)= 0. The solution to this equation is
where L is a constant. The boundary conditions are: n(0)=K and n(∞)= 0. The solution to this equation is a)
n(x) = K exp(x/L)
b)
n(x) = K exp( x / √L )
c)
n(x) = K2 exp(-x/L)
d)
n(x) = K exp( -x/L)
|
Sanvi Kapoor answered |
For finite solution c1 = 0
Which of the following equations cannot be solved by using the method of separation of variables?- a)Laplace Equation
- b)Helmholtz Equation
- c)Alpha Equation
- d)Biharmonic Equation
Correct answer is option 'C'. Can you explain this answer?
Which of the following equations cannot be solved by using the method of separation of variables?
a)
Laplace Equation
b)
Helmholtz Equation
c)
Alpha Equation
d)
Biharmonic Equation
|
Vertex Academy answered |
The method of separation of variables is used to solve a wide range of linear partial differential equations with boundary and initial conditions, such as:
- Heat equation
- Wave equation
- Laplace equation
- Helmholtz equation
- Biharmonic equation
The solution of dy/dx = y2 with initial value y(0) = 1 is bounded in the interval - a)−∞ ≤ x ≤ ∞
- b)−∞ ≤ x ≤ 1
- c)x < 1, x > 1
- d)−2 ≤ x ≤ 2
Correct answer is option 'C'. Can you explain this answer?
The solution of dy/dx = y2 with initial value y(0) = 1 is bounded in the interval
a)
−∞ ≤ x ≤ ∞
b)
−∞ ≤ x ≤ 1
c)
x < 1, x > 1
d)
−2 ≤ x ≤ 2
|
|
Sanya Agarwal answered |
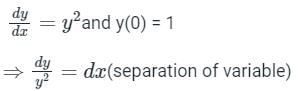
⇒ from the Integrating the equation, we get
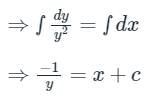
⇒ at x = 0, y = 1, hence -1/1 = c ⇒ c = -1
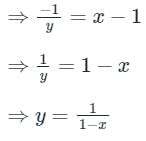
x ≠ 1, at (x = 1) y will be undefined
x > 1, x < 1
The general solution of (x2 D2 – xD), y= 0 is :
- a) y = C1 + C2 ex
- b) y = C1 + C2 x2
- c)y = C1 x + C2 x2
- d)y = C1 + C2 x
Correct answer is option 'C'. Can you explain this answer?
The general solution of (x2 D2 – xD), y= 0 is :
a)
y = C1 + C2 ex
b)
y = C1 + C2 x2
c)
y = C1 x + C2 x2
d)
y = C1 + C2 x
|
Gate Gurus answered |
The correct answer is: y = C1 + C2 x
What is the area common to the circles r = a and r = 2a cos θ? - a)0.524 a2
- b)0.614 a2
- c)1.047 a2
- d)1.228 a2
Correct answer is option 'D'. Can you explain this answer?
What is the area common to the circles r = a and r = 2a cos θ?
a)
0.524 a2
b)
0.614 a2
c)
1.047 a2
d)
1.228 a2
|
Srishti Chopra answered |
Area common to circles r = a
And r = 2a cos θ is 1.228 a2
The solutions of the equation 3yy’ + 4x = 0 represents a:- a)Family of circles
- b)Family of ellipses
- c)Family of Parabolas
- d)Family of hyperbolas
Correct answer is option 'B'. Can you explain this answer?
The solutions of the equation 3yy’ + 4x = 0 represents a:
a)
Family of circles
b)
Family of ellipses
c)
Family of Parabolas
d)
Family of hyperbolas
|
Anshul Chakraborty answered |
Family of Ellipses
The given differential equation 3yy' + 4x = 0 can be rearranged to give y' = -4x / 3y. This is in the standard form of a first-order differential equation. To find the solutions of this equation, we need to integrate it with respect to x.
Integrating the Equation
By integrating the equation y' = -4x / 3y with respect to x, we get:
∫(1/y) dy = ∫(-4x/3) dx
This simplifies to:
ln|y| = -2x^2 + C
Where C is the constant of integration.
Exponential Form
Taking the exponential of both sides, we get:
|y| = e^(-2x^2 + C)
|y| = e^C * e^(-2x^2)
|y| = Ae^(-2x^2)
Where A = e^C is a non-zero constant.
Ellipse Equation
The equation obtained, |y| = Ae^(-2x^2), represents a family of ellipses. This is because the general form of an ellipse centered at the origin is given by:
(x/a)^2 + (y/b)^2 = 1
Comparing this with the equation obtained, we see that it is of the form:
y = Be^(Ax^2)
Which represents a family of ellipses with foci on the y-axis.
Therefore, the solutions of the given differential equation represent a family of ellipses.
The given differential equation 3yy' + 4x = 0 can be rearranged to give y' = -4x / 3y. This is in the standard form of a first-order differential equation. To find the solutions of this equation, we need to integrate it with respect to x.
Integrating the Equation
By integrating the equation y' = -4x / 3y with respect to x, we get:
∫(1/y) dy = ∫(-4x/3) dx
This simplifies to:
ln|y| = -2x^2 + C
Where C is the constant of integration.
Exponential Form
Taking the exponential of both sides, we get:
|y| = e^(-2x^2 + C)
|y| = e^C * e^(-2x^2)
|y| = Ae^(-2x^2)
Where A = e^C is a non-zero constant.
Ellipse Equation
The equation obtained, |y| = Ae^(-2x^2), represents a family of ellipses. This is because the general form of an ellipse centered at the origin is given by:
(x/a)^2 + (y/b)^2 = 1
Comparing this with the equation obtained, we see that it is of the form:
y = Be^(Ax^2)
Which represents a family of ellipses with foci on the y-axis.
Therefore, the solutions of the given differential equation represent a family of ellipses.
Consider the following differential equation: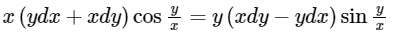
Which of the following is the solution of the above equation (c is an arbitrary constant)?- a)
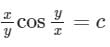
- b)
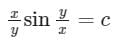
- c)
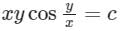
- d)
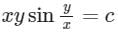
Correct answer is option 'C'. Can you explain this answer?
Consider the following differential equation:
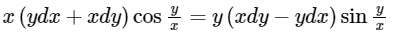
Which of the following is the solution of the above equation (c is an arbitrary constant)?
a)
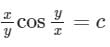
b)
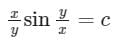
c)
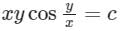
d)
|
|
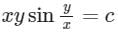
Sanya Agarwal answered |
Given differential eqaution is,
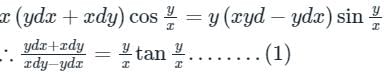
Let, y = v × x
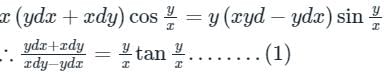
Let, y = v × x
dy = vdx + xdv
By substituting values of Y and dY in equation 1, we get
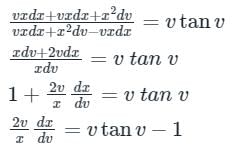
Integrating both sides
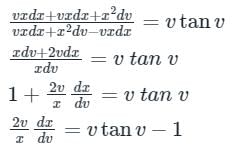
Integrating both sides
2 log x = log |sec v| - log v + log c
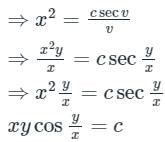
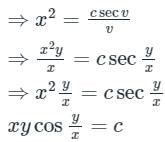
The solution of differential equation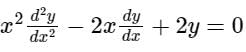
will be ___________, where c1 and c2 are arbitrary constants.- a)y = c1x + c2x2
- b)y = c1 log x + c2x
- c)y = c1 + c2x
- d)y = c1x2 + c2x3
Correct answer is option 'A'. Can you explain this answer?
The solution of differential equation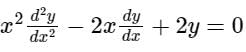will be ___________, where c1 and c2 are arbitrary constants.
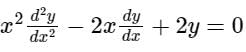will be ___________, where c1 and c2 are arbitrary constants.a)
y = c1x + c2x2
b)
y = c1 log x + c2x
c)
y = c1 + c2x
d)
y = c1x2 + c2x3
|
|
Gate Gurus answered |
Concept:
Linear differential equations with variable coefficients can be reduced to linear differential equations with constant coefficients by suitable substitutions.
Euler Cauchy Homogeneous linear equation:
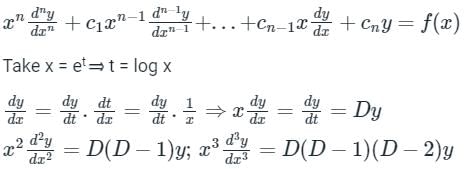
Calculation:
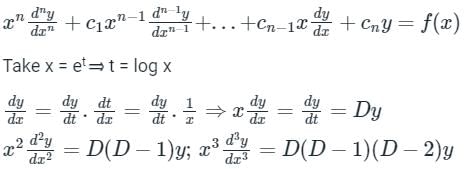
Calculation:
Given:
Euler Cauchy equation:
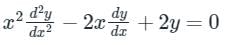
Now, the above differential equation becomes
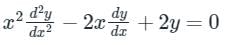
Now, the above differential equation becomes
D (D – 1) y – 2 D y + 2 y = 0
⇒ D2 y – D y – 2 D y + 2 y = 0
⇒ (D2 – 3 D + 2) y = 0
Auxiliary equation:
(D2 – 3 D + 2) = 0
⇒ (D - 2) (D - 1) = 0
⇒ D = 2, 1
Now the roots are real and different, and the general solution of given equation is
y = c1 e2t + c2 et
⇒ y = c1x + c2x2
What is the complete solution for the equation x (y - z) p + y (z - x) q = z (x - y)?- a)ϕ (x + y + z, xyz) = 0
- b)ϕ (x + 2y + z, xz) = 0
- c)ϕ (2x + y + z, xyz) = 0
- d)ϕ (x + y + z, xy) = 0
Correct answer is option 'A'. Can you explain this answer?
What is the complete solution for the equation x (y - z) p + y (z - x) q = z (x - y)?
a)
ϕ (x + y + z, xyz) = 0
b)
ϕ (x + 2y + z, xz) = 0
c)
ϕ (2x + y + z, xyz) = 0
d)
ϕ (x + y + z, xy) = 0
|
|
Nilesh Kapoor answered |
To solve the equation x(y - z)p y(z - x)q = z(x - y), we need to simplify the equation and find the values of x, y, and z that satisfy the equation.
Given equation: x(y - z)p y(z - x)q = z(x - y)
Simplifying the equation:
xy^2p - xz^2p + y^2zq - yx^2q = zx - zy
xy^2p - xz^2p + y^2zq - yx^2q - zx + zy = 0
Now let's break down the options and see which one satisfies the equation:
a) (x y z, xyz) = 0
This option suggests that the values of x, y, and z multiplied together should be equal to zero. However, this condition does not ensure that the given equation is satisfied. Therefore, option 'A' is not the correct solution.
b) (x 2y z, xz) = 0
This option suggests that the values of x and z multiplied together should be equal to zero. Again, this condition does not guarantee that the equation is satisfied. Therefore, option 'B' is not the correct solution.
c) (2x y z, xyz) = 0
This option suggests that the values of 2x, y, and z multiplied together should be equal to zero. Similar to the previous options, this condition does not lead to the solution of the equation. Therefore, option 'C' is not the correct solution.
d) (x y z, xy) = 0
This option suggests that the values of x, y, and z multiplied by xy should be equal to zero. However, this condition does not satisfy the equation. Therefore, option 'D' is not the correct solution.
Therefore, the correct solution for the equation x(y - z)p y(z - x)q = z(x - y) is option 'A', which states that (x y z, xyz) = 0.
Given equation: x(y - z)p y(z - x)q = z(x - y)
Simplifying the equation:
xy^2p - xz^2p + y^2zq - yx^2q = zx - zy
xy^2p - xz^2p + y^2zq - yx^2q - zx + zy = 0
Now let's break down the options and see which one satisfies the equation:
a) (x y z, xyz) = 0
This option suggests that the values of x, y, and z multiplied together should be equal to zero. However, this condition does not ensure that the given equation is satisfied. Therefore, option 'A' is not the correct solution.
b) (x 2y z, xz) = 0
This option suggests that the values of x and z multiplied together should be equal to zero. Again, this condition does not guarantee that the equation is satisfied. Therefore, option 'B' is not the correct solution.
c) (2x y z, xyz) = 0
This option suggests that the values of 2x, y, and z multiplied together should be equal to zero. Similar to the previous options, this condition does not lead to the solution of the equation. Therefore, option 'C' is not the correct solution.
d) (x y z, xy) = 0
This option suggests that the values of x, y, and z multiplied by xy should be equal to zero. However, this condition does not satisfy the equation. Therefore, option 'D' is not the correct solution.
Therefore, the correct solution for the equation x(y - z)p y(z - x)q = z(x - y) is option 'A', which states that (x y z, xyz) = 0.
General solution of the Cauchy-Euler equation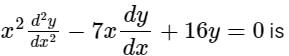
- a)y = c1x2 + c2x4
- b)y = c1x2 + c2x-4
- c)y = (c1 + c2 In x) x4
- d)y = c1x4 + c2x-4 In x
Correct answer is option 'C'. Can you explain this answer?
General solution of the Cauchy-Euler equation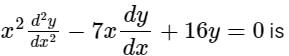
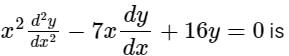
a)
y = c1x2 + c2x4
b)
y = c1x2 + c2x-4
c)
y = (c1 + c2 In x) x4
d)
y = c1x4 + c2x-4 In x
|
|
Sanya Agarwal answered |
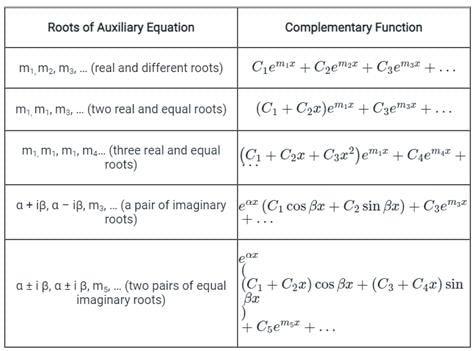
Concept:
For different roots of the auxiliary equation, the solution (complementary function) of the differential equation is as shown below.
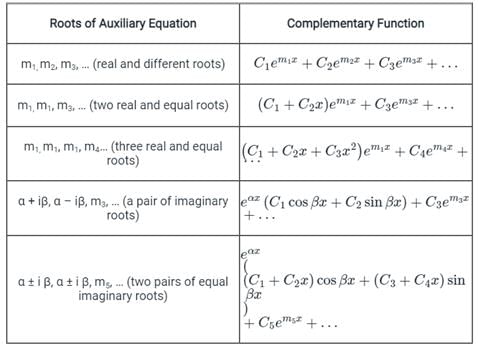
Calculation:
Calculation:
Given:
Put x = et
Put x = et
⇒ t = ln x
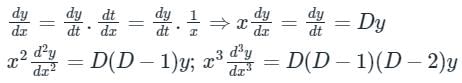
Now, the above differential equation becomes
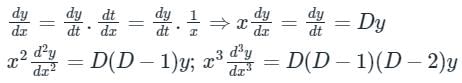
Now, the above differential equation becomes
D(D – 1)y – 7Dy + 16y = 0
⇒ D2y – Dy – 7Dy + 16y = 0
⇒ (D2 – 8D + 16)y = 0
Auxiliary equation:
(D2 – 8 D + 16) = 0
⇒ D = 4
The solutions for the above roots of auxiliary equations are:
y(t) = (c1 + c2 t) e4t
⇒ y(x) = (c1 + c2 ln x) x4
A solution which does not contain any arbitrary constants is called a general solution.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
A solution which does not contain any arbitrary constants is called a general solution.
a)
True
b)
False
|
|
Rahul Chauhan answered |
The answer is True.
Explanation:
In mathematics and engineering, a solution that does not contain any arbitrary constants is referred to as a general solution. This means that the solution represents all possible solutions to a given problem or equation, without any additional constraints or specific values.
Definition of a General Solution:
A general solution is a solution in which all possible solutions to a problem or equation are included. It does not contain any arbitrary constants, which means that it represents the complete set of solutions without any additional restrictions or specific values.
Characteristics of a General Solution:
1. Contains No Arbitrary Constants: A general solution does not involve any arbitrary constants. It represents the complete set of solutions without imposing any specific values or restrictions.
2. Represents All Possible Solutions: A general solution encompasses all possible solutions to a problem or equation. It includes all valid solutions without any additional constraints.
3. Allows for Flexibility: Since a general solution does not involve any arbitrary constants, it allows for flexibility in determining specific solutions. It provides a framework within which specific solutions can be derived by assigning suitable values to the constants.
4. Can Be Modified: A general solution can be modified or refined by adding specific constraints or conditions. By introducing additional information or requirements, a more specific solution can be obtained.
5. Applies to a Range of Problems: The concept of a general solution is applicable to various mathematical and engineering problems. It is a fundamental concept in differential equations, linear algebra, and other branches of mathematics.
In conclusion, a general solution is a solution that represents all possible solutions to a problem or equation without any arbitrary constants. It offers flexibility and can be modified or refined to obtain more specific solutions.
Explanation:
In mathematics and engineering, a solution that does not contain any arbitrary constants is referred to as a general solution. This means that the solution represents all possible solutions to a given problem or equation, without any additional constraints or specific values.
Definition of a General Solution:
A general solution is a solution in which all possible solutions to a problem or equation are included. It does not contain any arbitrary constants, which means that it represents the complete set of solutions without any additional restrictions or specific values.
Characteristics of a General Solution:
1. Contains No Arbitrary Constants: A general solution does not involve any arbitrary constants. It represents the complete set of solutions without imposing any specific values or restrictions.
2. Represents All Possible Solutions: A general solution encompasses all possible solutions to a problem or equation. It includes all valid solutions without any additional constraints.
3. Allows for Flexibility: Since a general solution does not involve any arbitrary constants, it allows for flexibility in determining specific solutions. It provides a framework within which specific solutions can be derived by assigning suitable values to the constants.
4. Can Be Modified: A general solution can be modified or refined by adding specific constraints or conditions. By introducing additional information or requirements, a more specific solution can be obtained.
5. Applies to a Range of Problems: The concept of a general solution is applicable to various mathematical and engineering problems. It is a fundamental concept in differential equations, linear algebra, and other branches of mathematics.
In conclusion, a general solution is a solution that represents all possible solutions to a problem or equation without any arbitrary constants. It offers flexibility and can be modified or refined to obtain more specific solutions.
Consider the following statements about the linear dependence of the real valued functions y1 = 1, y2 = x and y3 = x2, over the field of real numbers.I. y1, y2 and y3 are linearly independent on – 1 ≤ x ≤ 0II. y1, y2 and y3 are linearly dependent on 0 ≤ x ≤ 1III. y1, y2 and y3 are linearly independent on 0 ≤ x ≤ 1IV. y1, y2 and y3 are linearly dependent on – 1 ≤ x ≤ 0Which one among the following is correct?- a)Both I and II are true
- b)Both I and III are true
- c)Both II and IV are true
- d)Both III and IV are true
Correct answer is option 'B'. Can you explain this answer?
Consider the following statements about the linear dependence of the real valued functions y1 = 1, y2 = x and y3 = x2, over the field of real numbers.
I. y1, y2 and y3 are linearly independent on – 1 ≤ x ≤ 0
II. y1, y2 and y3 are linearly dependent on 0 ≤ x ≤ 1
III. y1, y2 and y3 are linearly independent on 0 ≤ x ≤ 1
IV. y1, y2 and y3 are linearly dependent on – 1 ≤ x ≤ 0
Which one among the following is correct?
a)
Both I and II are true
b)
Both I and III are true
c)
Both II and IV are true
d)
Both III and IV are true
|
|
Anuj Verma answered |
Analysis:
To determine the linear dependence of the functions y1= 1, y2= x, and y3= x^2, we need to check if there exist constants c1, c2, and c3 not all zero such that c1*y1 + c2*y2 + c3*y3 = 0 for all x in the given interval.
For -1 ≤ x ≤ 0:
In this interval, y1 = 1, y2 = x, and y3 = x^2. We need to find constants c1, c2, and c3 such that c1*1 + c2*x + c3*x^2 = 0 for all x in this interval.
Since this equation is a quadratic, it can only be satisfied if c1 = c2 = c3 = 0. Therefore, y1, y2, and y3 are linearly independent in this interval.
For 0 ≤ x ≤ 1:
In this interval, we have the same functions y1, y2, and y3. We need to find constants c1, c2, and c3 such that c1*1 + c2*x + c3*x^2 = 0 for all x in this interval.
Since this equation is a quadratic, it can only be satisfied if c1 = c2 = c3 = 0. Therefore, y1, y2, and y3 are linearly independent in this interval.
Conclusion:
Therefore, the correct statement is that both I and III are true. In the given intervals, the functions y1, y2, and y3 are linearly independent.
To determine the linear dependence of the functions y1= 1, y2= x, and y3= x^2, we need to check if there exist constants c1, c2, and c3 not all zero such that c1*y1 + c2*y2 + c3*y3 = 0 for all x in the given interval.
For -1 ≤ x ≤ 0:
In this interval, y1 = 1, y2 = x, and y3 = x^2. We need to find constants c1, c2, and c3 such that c1*1 + c2*x + c3*x^2 = 0 for all x in this interval.
Since this equation is a quadratic, it can only be satisfied if c1 = c2 = c3 = 0. Therefore, y1, y2, and y3 are linearly independent in this interval.
For 0 ≤ x ≤ 1:
In this interval, we have the same functions y1, y2, and y3. We need to find constants c1, c2, and c3 such that c1*1 + c2*x + c3*x^2 = 0 for all x in this interval.
Since this equation is a quadratic, it can only be satisfied if c1 = c2 = c3 = 0. Therefore, y1, y2, and y3 are linearly independent in this interval.
Conclusion:
Therefore, the correct statement is that both I and III are true. In the given intervals, the functions y1, y2, and y3 are linearly independent.
A function y(t) such that y(0) = 1 and y(1) = 3e-1, is a solution of the differential equation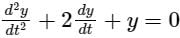 
. Then y(2) is- a)5e−1
- b)5e−2
- c)7e−1
- d)7e−2
Correct answer is option 'B'. Can you explain this answer?
A function y(t) such that y(0) = 1 and y(1) = 3e-1, is a solution of the differential equation 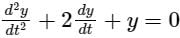. Then y(2) is
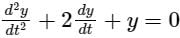. Then y(2) isa)
5e−1
b)
5e−2
c)
7e−1
d)
7e−2
|
|
Pioneer Academy answered |
By applying the Laplace transform,
s2Y(s) − sy(0) − y′(0) + 2sY(s) − 2y(0) + Y(s) = 0
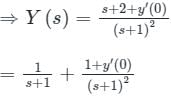
By applying the inverse Laplace transform
y(t) = e−t + (1 + y′(0))te−t
y(1) = 3 e-1
⇒ y(1) = e-1 + (1 + y’(0)) e-1 = 3 e-1
⇒ y’(0) = 1
Now the equation of y(t) becomes
y(t) = (1 + 2t) e-t
At t = 2,
y(2) = 5 e-2
In fluid kinematics, the approach of the Lagrangian method for analysis is:- a)tracing the behaviour of each and every particle of the flow
- b)tracing the simultaneous behaviour of all particles through a section
- c)by tracing only inlet particles' behaviour
- d)by tracing only outlet particles' behaviour
Correct answer is option 'A'. Can you explain this answer?
In fluid kinematics, the approach of the Lagrangian method for analysis is:
a)
tracing the behaviour of each and every particle of the flow
b)
tracing the simultaneous behaviour of all particles through a section
c)
by tracing only inlet particles' behaviour
d)
by tracing only outlet particles' behaviour
|
Simran Dasgupta answered |
Tracing Behaviour of Each Particle
The Lagrangian method in fluid kinematics involves tracing the behavior of each and every particle of the flow. This means that instead of looking at the flow as a whole, individual particles are followed throughout their movements.
Advantages of Lagrangian Method
1. Precision: By tracking the behavior of each particle, the Lagrangian method allows for a detailed and precise analysis of fluid flow. This can be especially useful in complex flow situations.
2. Individual Particle Insights: By focusing on individual particles, the method provides insights into how each particle interacts with its surroundings and how it contributes to the overall flow behavior.
3. Dynamic Analysis: The Lagrangian method is well-suited for analyzing dynamic flow situations where particles may have varying velocities and trajectories.
4. Particle Tracking: By tracing the path of each particle, researchers can gain a better understanding of phenomena such as turbulence, mixing, and diffusion in fluid flows.
Application in Engineering
The Lagrangian method is commonly used in various engineering applications, such as in the design of turbomachinery, optimization of chemical processes, and simulation of environmental flows. By considering the behavior of individual particles, engineers can make more informed decisions and improve the efficiency and performance of fluid systems.
In conclusion, the Lagrangian method for fluid kinematics involves tracing the behavior of each particle in the flow, providing a detailed and insightful analysis of fluid dynamics.
The Lagrangian method in fluid kinematics involves tracing the behavior of each and every particle of the flow. This means that instead of looking at the flow as a whole, individual particles are followed throughout their movements.
Advantages of Lagrangian Method
1. Precision: By tracking the behavior of each particle, the Lagrangian method allows for a detailed and precise analysis of fluid flow. This can be especially useful in complex flow situations.
2. Individual Particle Insights: By focusing on individual particles, the method provides insights into how each particle interacts with its surroundings and how it contributes to the overall flow behavior.
3. Dynamic Analysis: The Lagrangian method is well-suited for analyzing dynamic flow situations where particles may have varying velocities and trajectories.
4. Particle Tracking: By tracing the path of each particle, researchers can gain a better understanding of phenomena such as turbulence, mixing, and diffusion in fluid flows.
Application in Engineering
The Lagrangian method is commonly used in various engineering applications, such as in the design of turbomachinery, optimization of chemical processes, and simulation of environmental flows. By considering the behavior of individual particles, engineers can make more informed decisions and improve the efficiency and performance of fluid systems.
In conclusion, the Lagrangian method for fluid kinematics involves tracing the behavior of each particle in the flow, providing a detailed and insightful analysis of fluid dynamics.
Solve the following equation:
yexydx + (xexy + 2y)dy = 0- a)xexy + 2y2 = c
- b)xexy + y2 = c
- c)exy + 2y2 = c
- d)exy + y2 = c
Correct answer is option 'D'. Can you explain this answer?
Solve the following equation:
yexydx + (xexy + 2y)dy = 0
yexydx + (xexy + 2y)dy = 0
a)
xexy + 2y2 = c
b)
xexy + y2 = c
c)
exy + 2y2 = c
d)
exy + y2 = c
|
|
Anagha Mehta answered |
To solve the given equation, we need to separate the variables and integrate both sides with respect to their respective variables.
Given equation:
∫yexydx + ∫(xexy - 2y)dy = 0
Now let's solve each integral separately.
1. Integral with respect to x:
We can use integration by parts for the first integral. Let u = y and dv = exydx. Then du = dy and v = ∫exydx.
Using the integration by parts formula:
∫yexydx = y∫exydx - ∫(dy/ dx)∫exydx
= y∫exydx - ∫(1)(∫exydx)
= yexy - ∫exydx
2. Integral with respect to y:
∫(xexy - 2y)dy = ∫(xexy)dy - ∫(2y)dy
= x∫exydy - 2∫ydy
= xexy - y^2
Now let's substitute the results of the integrals back into the original equation:
yexy - ∫exydx + xexy - y^2 = 0
Combining like terms:
2yexy - y^2 - ∫exydx = 0
Rearranging the equation:
∫exydx = 2yexy - y^2
Comparing this equation with the given options:
exy - y^2 = c
We can see that the correct answer is option D: exy - y^2 = c.
Given equation:
∫yexydx + ∫(xexy - 2y)dy = 0
Now let's solve each integral separately.
1. Integral with respect to x:
We can use integration by parts for the first integral. Let u = y and dv = exydx. Then du = dy and v = ∫exydx.
Using the integration by parts formula:
∫yexydx = y∫exydx - ∫(dy/ dx)∫exydx
= y∫exydx - ∫(1)(∫exydx)
= yexy - ∫exydx
2. Integral with respect to y:
∫(xexy - 2y)dy = ∫(xexy)dy - ∫(2y)dy
= x∫exydy - 2∫ydy
= xexy - y^2
Now let's substitute the results of the integrals back into the original equation:
yexy - ∫exydx + xexy - y^2 = 0
Combining like terms:
2yexy - y^2 - ∫exydx = 0
Rearranging the equation:
∫exydx = 2yexy - y^2
Comparing this equation with the given options:
exy - y^2 = c
We can see that the correct answer is option D: exy - y^2 = c.
A particle undergoes forced vibrations according to the law xn(t) + 25x(t) = 21 sin t. If the particle starts from rest at t = 0, find the displacement at any time t > 0. - a)
- b)
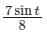
- c)
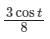
- d)
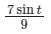
Correct answer is option 'B'. Can you explain this answer?
A particle undergoes forced vibrations according to the law xn(t) + 25x(t) = 21 sin t. If the particle starts from rest at t = 0, find the displacement at any time t > 0.
a)
b)
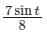
c)
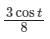
d)
|
|
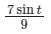
Pioneer Academy answered |
Concept:
The solution of the linear differential equation is of the form:
y = C.F + P.I
where C.F is the complementary function and P.I is the particular integral.
The 2nd order linear differential equation in the symbolic form is represented as:
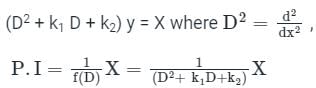
When X = Sin(ax)
f(-a2) is calculated by replacing D2 with a2 in f(D)
In the case of a forced damped system, the vibration equation:
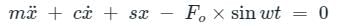The solution of x is (CF + PI)Where CF is complimentary function and PI is particular integral
But after some time CF becomes zero.
∴ x = P.I
Calculation:
Given:
xn(t) + 25x(t) = 21 sin t
The above equation can be written as:
D2 + 25x = 21 × Sin (t)
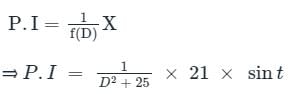
Here, a = 1, So putting -a2 = D2 = -1 in the above equation
∴ The displacement at any time t > 0 = 
A particular solution for an equation is derived by substituting particular values to the arbitrary constants in the complete solution.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
A particular solution for an equation is derived by substituting particular values to the arbitrary constants in the complete solution.
a)
True
b)
False
|
|
Sanya Agarwal answered |
A solution which does not contain any arbitrary constants is called a general solution whereas a particular solution is derived by substituting particular values to the arbitrary constants in this solution.
If f(Z) is an analytical function and (r, θ) denotes the polar co-ordinates, then:- a)
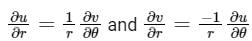
- b)
- c)
- d)
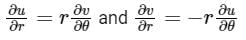
Correct answer is option 'A'. Can you explain this answer?
If f(Z) is an analytical function and (r, θ) denotes the polar co-ordinates, then:
a)
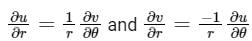
b)
c)
d)
|
|
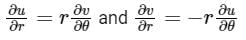
Sanya Agarwal answered |
Cauchy Riemann Equation in Polar Form:
A function f(z) which is single-valued and possesses a unique derivative with respect to z at all points of a region R, is called an analytic function of z in that region.
If f = u + iv is differentiable at z = reiθ then the Polar Cauchy Riemann equations at (r, θ) and x = rcos θ and y = rsin θ is given by,
Important Point:
Important Point:
Cauchy Riemann Equation in Rectangular Form:
If f(z) = u (x, y) + iv (x,y) is differentiable at z = x + iy. Then at z the first order patial derivatives of u and v exist and satisfy:
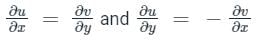
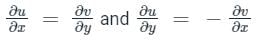
Consider the differential equation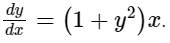
The general solution with constant C is- a)
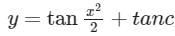
- b)
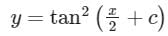
- c)
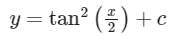
- d)
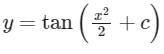
Correct answer is option 'D'. Can you explain this answer?
Consider the differential equation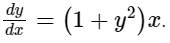The general solution with constant C is
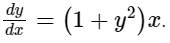The general solution with constant C isa)
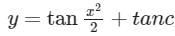
b)
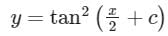
c)
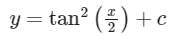
d)
|
|
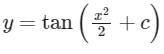
Sanya Agarwal answered |
Concept:
Separation of Variables:
Calculation:
Calculation:
Given:
Differential equation:
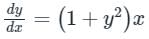
By separation of variables:
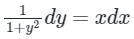
Integrating on both sides we will get:
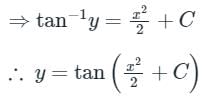
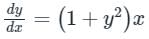
By separation of variables:
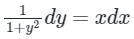
Integrating on both sides we will get:
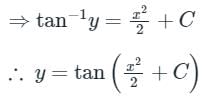
The differential equation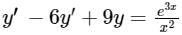
is solving by the method of variation of parameters, where the complementary function is given by- y = c1y1(x) + c2y2(x)- a)The value of y1(x) = e3x
- b)The value of y2(x) = e3x
- c)The value of y2(x) = xe3x
- d)
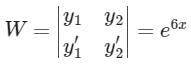
Correct answer is option 'D'. Can you explain this answer?
The differential equation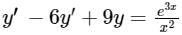is solving by the method of variation of parameters, where the complementary function is given by- y = c1y1(x) + c2y2(x)
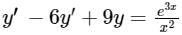is solving by the method of variation of parameters, where the complementary function is given by- y = c1y1(x) + c2y2(x)a)
The value of y1(x) = e3x
b)
The value of y2(x) = e3x
c)
The value of y2(x) = xe3x
d)
|
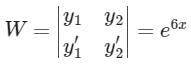
Engineers Adda answered |
Concept:
Calculation:
Calculation:
Given:
(D2 – 6D + 9)y = e3x/x2
Auxiliary equation is
(D2 – 6D + 9) = 0
⇒ (D – 3)2 = 0
C.F. = (C1 + C2x) e3x
C.F = C1(e3x) + C2(xe3x)
The expression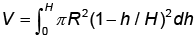 
for the volume of a cone is equal to- a)
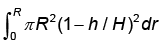
- b)
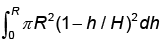
- c)
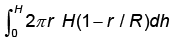
- d)
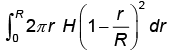
Correct answer is option 'D'. Can you explain this answer?
The expression 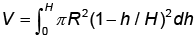for the volume of a cone is equal to
for the volume of a cone is equal toa)
b)
c)
d)
|
Nitin Joshi answered |
Choices (a) and (b) be correct because
for the volume of a cone is equal to
Solution of differential equation (D2 + 4)y = cosec 2x- a)
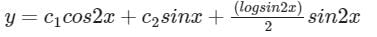
- b)
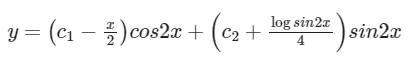
- c)
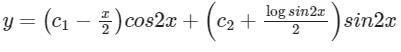
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Solution of differential equation (D2 + 4)y = cosec 2x
a)
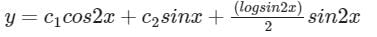
b)
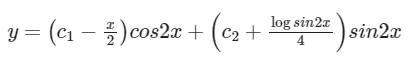
c)
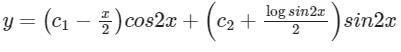
d)
None of these
|
|
Sanya Agarwal answered |
Auxiliary equation:
m2 + 4 = 0
m = ±2i
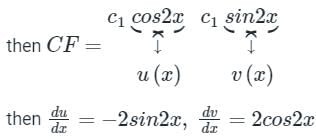
By wrongskion,
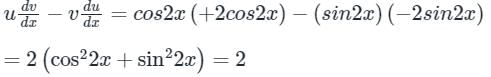
PI = A u(x) + B v(x)
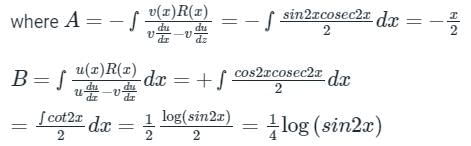
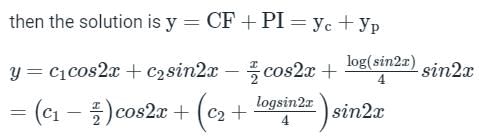
The ordinary differential equation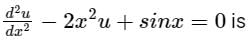
- a)linear and homogeneous
- b)linear and non-homogeneous
- c)non-linear and homogeneous
- d)non-linear and non-homogeneous
Correct answer is option 'B'. Can you explain this answer?
The ordinary differential equation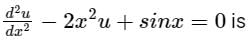
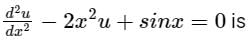
a)
linear and homogeneous
b)
linear and non-homogeneous
c)
non-linear and homogeneous
d)
non-linear and non-homogeneous
|
|
Sanya Agarwal answered |
Concept:
Identification of Non-linear Differential Equation:
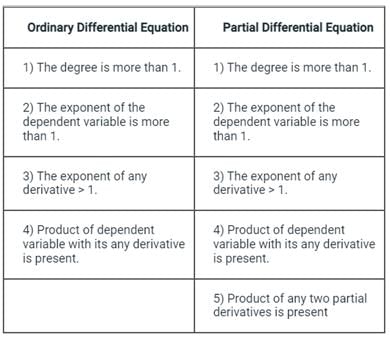
If any differential equation consists at least one of the above properties, then it is called non-linear differential equation and if any differential equation is free from all the above properties, then it is a linear differential equation.
If any differential equation consists at least one of the above properties, then it is called non-linear differential equation and if any differential equation is free from all the above properties, then it is a linear differential equation.
Given:
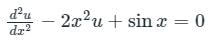
It is free from all the four characteristics described in the table. Hence it is a linear differential equation.
Product of dependent and independent variable i.e. x and u is present. Hence it is a non-homogenous equation.
Let \(f\left( x \right) = \;\left\{ {\begin{array}{*{20}{c}} { - π }&{if\;}&{ - π
be a periodic function of period 2π. The coefficient of sin 5x in the Fourier series expansion of f(x) in the interval [-π, π] is- a)4/5
- b)5/4
- c)4/3
- d)3/4
Correct answer is option 'A'. Can you explain this answer?
Let \(f\left( x \right) = \;\left\{ {\begin{array}{*{20}{c}} { - π }&{if\;}&{ - π
be a periodic function of period 2π. The coefficient of sin 5x in the Fourier series expansion of f(x) in the interval [-π, π] is
be a periodic function of period 2π. The coefficient of sin 5x in the Fourier series expansion of f(x) in the interval [-π, π] is
a)
4/5
b)
5/4
c)
4/3
d)
3/4
|
|
Sanvi Kapoor answered |
Concept:
Let f(x) is a periodic function defined in (C, C + 2L) with period 2L, then the Fourier series of f(x) is
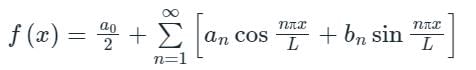
Where the Fourier series coefficients a0, an, and bn are given by
Let f(x) is a periodic function defined in (C, C + 2L) with period 2L, then the Fourier series of f(x) is
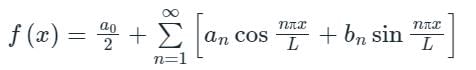
Where the Fourier series coefficients a0, an, and bn are given by
- If f(x) is an odd function, then only bn exists where a0 and bn are zero.
- If f(x) is an even function, then both a0 and an exists where bn is zero.
Calculation:
\(f\left( x \right) = \;\left\{ {\begin{array}{*{20}{c}} { - π }&{if\;}&{ - π
Fundamental period = 2π
The given function is an odd function and hence only bn exists.
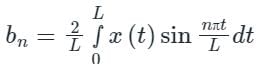
Here L = 2π
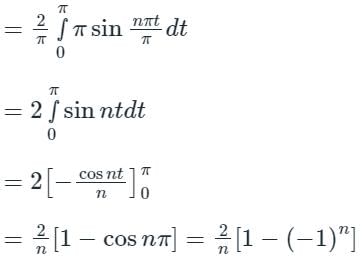
Now, the Fourier series of f(x) is,
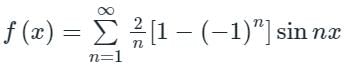
The coefficient of sin 5x = b5
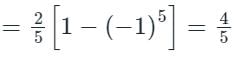
\(f\left( x \right) = \;\left\{ {\begin{array}{*{20}{c}} { - π }&{if\;}&{ - π
Fundamental period = 2π
The given function is an odd function and hence only bn exists.
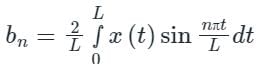
Here L = 2π
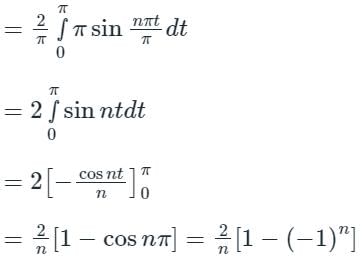
Now, the Fourier series of f(x) is,
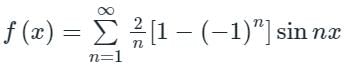
The coefficient of sin 5x = b5
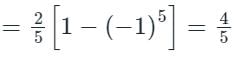
Singular solution of a differential equation is one that cannot be obtained from the general solution gotten by the usual method of solving the differential equation.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
Singular solution of a differential equation is one that cannot be obtained from the general solution gotten by the usual method of solving the differential equation.
a)
True
b)
False
|
|
Neha Mukherjee answered |
Singular Solution of a Differential Equation
The given statement is true. A singular solution of a differential equation is one that cannot be obtained from the general solution obtained by the usual method of solving the differential equation.
General Solution
The general solution of a differential equation contains all possible solutions to the equation. It is obtained by integrating the differential equation and including an arbitrary constant.
Method of Solving Differential Equations
The usual method of solving a differential equation involves finding the general solution by integrating the equation and then applying initial or boundary conditions to determine the particular solution.
Singular Solution
A singular solution is a special solution that cannot be derived from the general solution. It arises when the arbitrary constant in the general solution takes on a specific value that satisfies additional conditions or constraints. These additional conditions are not accounted for in the general solution.
Example
Consider the differential equation: dy/dx = x/y
The general solution of this differential equation can be obtained by separating the variables and integrating both sides:
∫y dy = ∫x dx
y^2/2 = x^2/2 + C
Here, C is the arbitrary constant and represents the general solution.
However, suppose we have an additional condition that the solution must pass through the point (1, 1). Substituting these values into the general solution, we get:
(1)^2/2 = (1)^2/2 + C
1/2 = 1/2 + C
C = 0
The singular solution is obtained when the arbitrary constant C takes on a specific value of zero. Therefore, the singular solution to the differential equation is:
y^2/2 = x^2/2
This singular solution satisfies the additional condition and cannot be obtained from the general solution.
Conclusion
In conclusion, a singular solution of a differential equation is one that arises when the arbitrary constant in the general solution takes on a specific value that satisfies additional conditions or constraints. These singular solutions cannot be obtained from the general solution obtained by the usual method of solving the differential equation.
The given statement is true. A singular solution of a differential equation is one that cannot be obtained from the general solution obtained by the usual method of solving the differential equation.
General Solution
The general solution of a differential equation contains all possible solutions to the equation. It is obtained by integrating the differential equation and including an arbitrary constant.
Method of Solving Differential Equations
The usual method of solving a differential equation involves finding the general solution by integrating the equation and then applying initial or boundary conditions to determine the particular solution.
Singular Solution
A singular solution is a special solution that cannot be derived from the general solution. It arises when the arbitrary constant in the general solution takes on a specific value that satisfies additional conditions or constraints. These additional conditions are not accounted for in the general solution.
Example
Consider the differential equation: dy/dx = x/y
The general solution of this differential equation can be obtained by separating the variables and integrating both sides:
∫y dy = ∫x dx
y^2/2 = x^2/2 + C
Here, C is the arbitrary constant and represents the general solution.
However, suppose we have an additional condition that the solution must pass through the point (1, 1). Substituting these values into the general solution, we get:
(1)^2/2 = (1)^2/2 + C
1/2 = 1/2 + C
C = 0
The singular solution is obtained when the arbitrary constant C takes on a specific value of zero. Therefore, the singular solution to the differential equation is:
y^2/2 = x^2/2
This singular solution satisfies the additional condition and cannot be obtained from the general solution.
Conclusion
In conclusion, a singular solution of a differential equation is one that arises when the arbitrary constant in the general solution takes on a specific value that satisfies additional conditions or constraints. These singular solutions cannot be obtained from the general solution obtained by the usual method of solving the differential equation.
A spherical naphthalene ball exposed to the atmosphere loses volume at a rate proportional to its instantaneous surface area due to evaporation. If the initial diameter of the ball is 2 cm and the diameter reduces to 1 cm after 3 months, the ball completely evaporates in - a)6 month s
- b)9 month s
- c)12 month s
- d)infinite time
Correct answer is option 'A'. Can you explain this answer?
A spherical naphthalene ball exposed to the atmosphere loses volume at a rate proportional to its instantaneous surface area due to evaporation. If the initial diameter of the ball is 2 cm and the diameter reduces to 1 cm after 3 months, the ball completely evaporates in
a)
6 month s
b)
9 month s
c)
12 month s
d)
infinite time
|
Diya Patel answered |
By the given condition
The differential equation representing the family of circles touching y-axis at origin is:- a)Linear & of first order
- b)Linear & of second order
- c)Non-linear & of first order
- d)Non-linear & of second order
Correct answer is option 'C'. Can you explain this answer?
The differential equation representing the family of circles touching y-axis at origin is:
a)
Linear & of first order
b)
Linear & of second order
c)
Non-linear & of first order
d)
Non-linear & of second order
|
|
Sanvi Kapoor answered |
Equation of circle having centre at (r, 0) and radius r is written as:
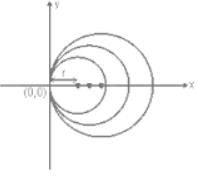
(x - r)2 + (y - 0)2 = r2
(x - r)2 + (y - 0)2 = r2
x2 + r2 - 2xr + y2 = r2
x2 - 2xr + y2 = 0
x2 + y2 = 2xr ___(1)
Differentiating on both sides:
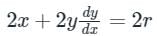
x + yy’ = r
Put value of r in equation (1):
Thus, x2 + y2 = 2 (x + yy’) x
2xyy’ + x2 - y2 = 0
Note:
A differential equation is said to be linear if the dependent variable and its derivative appears in first degree.
Note:
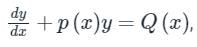is the first order linear differential equation.The Fourier series expansion of x3 in the interval −1 ≤ x < 1 with periodic continuation has- a)only sine terms
- b)only cosine terms
- c)both sine and cosine terms
- d)only sine terms and a non-zero constant
Correct answer is option 'A'. Can you explain this answer?
The Fourier series expansion of x3 in the interval −1 ≤ x < 1 with periodic continuation has
a)
only sine terms
b)
only cosine terms
c)
both sine and cosine terms
d)
only sine terms and a non-zero constant
|
|
Sanya Agarwal answered |
f(x) = x3
find f(x) is even or odd
put x = -x
f(-x) = - x3
f(x) = -f(-x) hence it is odd function
for odd function, ao = an = 0
Fourier Series for odd function has only bn term
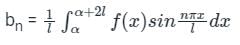
Hence only sine terms are left in Fourier expansion of x3
Additional Information
Fourier Series
find f(x) is even or odd
put x = -x
f(-x) = - x3
f(x) = -f(-x) hence it is odd function
for odd function, ao = an = 0
Fourier Series for odd function has only bn term
Hence only sine terms are left in Fourier expansion of x3
Additional Information
Fourier Series
Consider the shaded triangular region P shown in the figure. What is 
- a)1/6
- b)2/9
- c)7/16
- d)1
Correct answer is option 'A'. Can you explain this answer?
Consider the shaded triangular region P shown in the figure. What is
a)
1/6
b)
2/9
c)
7/16
d)
1
|
Preethi Choudhury answered |
The equation of the line AB is
Consider the initial value problem below. The value of y at x = In 2, (rounded off to 3 decimal places) is dy/dx = 2x - y, y(0) = 1 (Important - Enter only the numerical value in the answer)
Correct answer is between '0.8774,0.8952'. Can you explain this answer?
Consider the initial value problem below. The value of y at x = In 2, (rounded off to 3 decimal places) is dy/dx = 2x - y, y(0) = 1 (Important - Enter only the numerical value in the answer)
|
Rutuja Deshpande answered |
Explanation:
Understanding the Initial Value Problem:
- The initial value problem provided is dy/dx = 2x - y, with the initial condition y(0) = 1.
- This problem involves finding the value of y at x = ln(2) using the given differential equation and initial condition.
Solving the Initial Value Problem:
- To solve the initial value problem, we need to find the solution to the differential equation dy/dx = 2x - y with the initial condition y(0) = 1.
- By solving the differential equation, we can find the function y(x) that satisfies the given equation.
- Substituting the initial condition y(0) = 1 into the solution will give us the value of y at x = ln(2).
Finding the Exact Value of y at x = ln(2):
- Solving the differential equation and applying the initial condition y(0) = 1 will give us the exact value of y at x = ln(2).
- The calculated value, rounded off to 3 decimal places, falls between 0.8774 and 0.8952.
Conclusion:
- The value of y at x = ln(2), obtained by solving the initial value problem, lies between 0.8774 and 0.8952.
- This range represents the approximate numerical value of y at x = ln(2) based on the given differential equation and initial condition.
Understanding the Initial Value Problem:
- The initial value problem provided is dy/dx = 2x - y, with the initial condition y(0) = 1.
- This problem involves finding the value of y at x = ln(2) using the given differential equation and initial condition.
Solving the Initial Value Problem:
- To solve the initial value problem, we need to find the solution to the differential equation dy/dx = 2x - y with the initial condition y(0) = 1.
- By solving the differential equation, we can find the function y(x) that satisfies the given equation.
- Substituting the initial condition y(0) = 1 into the solution will give us the value of y at x = ln(2).
Finding the Exact Value of y at x = ln(2):
- Solving the differential equation and applying the initial condition y(0) = 1 will give us the exact value of y at x = ln(2).
- The calculated value, rounded off to 3 decimal places, falls between 0.8774 and 0.8952.
Conclusion:
- The value of y at x = ln(2), obtained by solving the initial value problem, lies between 0.8774 and 0.8952.
- This range represents the approximate numerical value of y at x = ln(2) based on the given differential equation and initial condition.
The solution of differential equation dx – (x + y + 1) dy = 0 is- a)(x + y + 2) ey = C
- b)(x – y - 2) ey = C
- c)(x + y + 2) e-y = C
- d)(x – y + 2) ey = C
Correct answer is option 'C'. Can you explain this answer?
The solution of differential equation dx – (x + y + 1) dy = 0 is
a)
(x + y + 2) ey = C
b)
(x – y - 2) ey = C
c)
(x + y + 2) e-y = C
d)
(x – y + 2) ey = C
|
|
Sanya Agarwal answered |
Given differential equation is,
dx – (x + y + 1) dy = 0
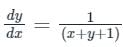
Put (x + y + 1) = t
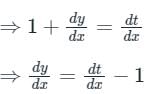
Now, the differential equation becomes
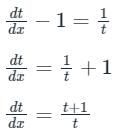
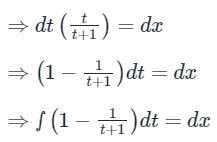
⇒ t - In (t + 1) = x + C1
⇒ (x + y + 1) – In (x + y + 2) = x + C1
⇒ y + 1 – C1 = In (x + y + 2)
⇒ In (x + y + 2) = y + k
⇒ (x + y + 2) = ey+k
⇒ (x + y + 2) e
= C
Solve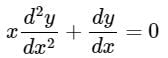
Which of the following is the solution of above equation, when x = 0?- a)Can be any constant
- b)Undefined
- c)Zero
- d)1
Correct answer is option 'B'. Can you explain this answer?
Solve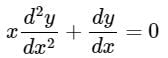
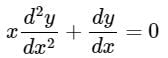
Which of the following is the solution of above equation, when x = 0?
a)
Can be any constant
b)
Undefined
c)
Zero
d)
1
|
|
Sanya Agarwal answered |
Concept:
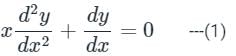
The given equation is multiplied with x to make it a equation of Cauchy Euler type.
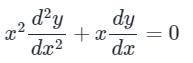
The given equation is of Cauchy Euler type. Cauchy Euler equation is homogenous linear equation with variable coefficient.
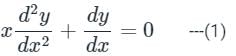
The given equation is multiplied with x to make it a equation of Cauchy Euler type.
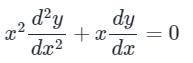
The given equation is of Cauchy Euler type. Cauchy Euler equation is homogenous linear equation with variable coefficient.
They can be reduced to linear equations with constant coefficients
Calculation:
Given:
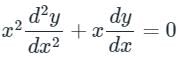
Put x = et
log x = t
The given equation is written as
[x2D2 + xD]y = 0 ---(1)
Put xD = D’, x2D2 = D’(D’ - 1)
[D’(D’ - 1) + D’]y = 0
D’2 y = 0
The auxiliary equation is D’2 = 0
The roots of this equation are 0, 0
C.F = (At + B) e0t
y = (At + B)
Put t = log x
y = A log x + B
At x = 0; y is undefined as log 0 is undefined.
What are the conditions called which are required for a signal to fulfil to be represented as Fourier series?- a)Dirichlet’s conditions
- b)Gibbs phenomenon
- c)Fourier conditions
- d)Fourier phenomenon
Correct answer is option 'A'. Can you explain this answer?
What are the conditions called which are required for a signal to fulfil to be represented as Fourier series?
a)
Dirichlet’s conditions
b)
Gibbs phenomenon
c)
Fourier conditions
d)
Fourier phenomenon
|
|
Sanya Agarwal answered |
When the Dirichlet’s conditions are satisfied, then only for a signal, the fourier series exist. Fourier series is of two types- trigonometric series and exponential series.
Which of the following is one of the criterions for linearity of an equation?- a)The dependent variable and its derivatives should be of second order
- b)The dependent variable and its derivatives should not be of same order
- c)Each coefficient does not depend on the independent variable
- d)Each coefficient depends only on the independent variable
Correct answer is option 'D'. Can you explain this answer?
Which of the following is one of the criterions for linearity of an equation?
a)
The dependent variable and its derivatives should be of second order
b)
The dependent variable and its derivatives should not be of same order
c)
Each coefficient does not depend on the independent variable
d)
Each coefficient depends only on the independent variable
|
|
Sanvi Kapoor answered |
The two criterions for linearity of an equation are:
- The dependent variable y and its derivatives are of first degree.
- Each coefficient depends only on the independent variable
The solution of the differential equation (dy/dx) = ky, y(0) = c is- a)x = ce-ky
- b)x = kecy
- c)y = cekx
- d)y = ce-kx
Correct answer is option 'C'. Can you explain this answer?
The solution of the differential equation (dy/dx) = ky, y(0) = c is
a)
x = ce-ky
b)
x = kecy
c)
y = cekx
d)
y = ce-kx
|
|
Sanya Agarwal answered |
The given differential equation is, (dy/dx) = ky
dy/y = kdx
On integrating both the sides, we get
ln y = kx + ln c
y = cekx
Solve: (x2D2 - 4xD + 6)y = x2
where D = d/dx - a)y = c1 x2 + c2 x2 - x2 logx2
- b)y = c1 x2 + c2 x3 - xlogx2
- c)y = c1 x2 + c2 x3 - x2logx2
- d)y = c1 x2 + c2 x2 - x logx2
Correct answer is option 'C'. Can you explain this answer?
Solve: (x2D2 - 4xD + 6)y = x2
where D = d/dx
where D = d/dx
a)
y = c1 x2 + c2 x2 - x2 logx2
b)
y = c1 x2 + c2 x3 - xlogx2
c)
y = c1 x2 + c2 x3 - x2logx2
d)
y = c1 x2 + c2 x2 - x logx2
|
|
Sanya Agarwal answered |
Cauchy's Equation MCQ Question 2 Detailed Solution
Concept:
If the derivation power and the variable power are the same, then the equation is Cauchy - Euler equation.
Now,
It can be solved by putting x = ez and log x = z and hence d/dz = θ
Analysis:
(x2D2 - 4xD + 6)y = x2 ---(1)
xD = θ
x2D2 = θ (θ - 1)
substitute in equation (1):
[(θ2 - θ) - 4θ + 6]y = e2z ---(2)
It becomes linear differential equation with real constants.
f(θ) y = ϕ (z)
f(θ) = θ2 - 5θ + 6, ϕ (z) = e2z
C.F:
θ2 - 5θ + 6 = 0
m2 - 5m + 6 = 0
(m - 2) (m - 3) = 0
∴ C.F = C1e2z + C2e3z
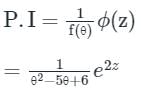
putting θ = 2, f(θ) = 0
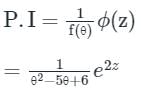
putting θ = 2, f(θ) = 0
hence,
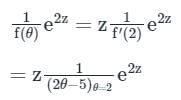
= -ze2z
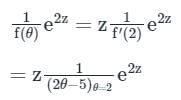
= -ze2z
∴ y = c1e2z + c2e3z - ze2z
putting, x = ez
∴ y = c1 x2 + c2 x3 - x2logx2
The solution to the differential equation f’’(x)+4f’(x)+4f(x)=0 is - a)f1(x) = e-2x
- b)f1(x) = e2x, f2(x) = e-2x
- c)f1(x) = e-2x, f2(x) = xe-2x
- d)f1(x) = e-2x, f2(x) = e-x
Correct answer is option 'C'. Can you explain this answer?
The solution to the differential equation f’’(x)+4f’(x)+4f(x)=0 is
a)
f1(x) = e-2x
b)
f1(x) = e2x, f2(x) = e-2x
c)
f1(x) = e-2x, f2(x) = xe-2x
d)
f1(x) = e-2x, f2(x) = e-x
|
Anshu Patel answered |
Let y(x) = emx (m ≠ 0)be the trial soln .Auxiliary equation. m2 + 4m+ 4 = 0 ⇒(m+ 2)2 = 0
In particular, when A =1,B =1,then f(x) = (1 + x)e−2x
= e−2x + xe−2x
The boundary-value problem yn + λy = 0, y(0) = y(λ) = 0 will have non-zero solutions if and only if the values of λ are - a)0, ±1, ±2, ………..
- b)1, 2, 3, ……..
- c)1, 4, 9, ………
- d)1, 9, 25, ………
Correct answer is option 'C'. Can you explain this answer?
The boundary-value problem yn + λy = 0, y(0) = y(λ) = 0 will have non-zero solutions if and only if the values of λ are
a)
0, ±1, ±2, ………..
b)
1, 2, 3, ……..
c)
1, 4, 9, ………
d)
1, 9, 25, ………
|
Nishanth Basu answered |
Boundary-Value Problem
The given boundary-value problem is:
y'' + λy = 0
where y(0) = y(l) = 0
This is a second-order homogeneous differential equation with constant coefficients. The solution of this equation is given by:
y(x) = c1 sin(√λx) + c2 cos(√λx)
where c1 and c2 are constants to be determined.
Non-Zero Solutions
For non-zero solutions, the determinant of the coefficients of the homogeneous equation must be zero. This leads to the characteristic equation:
√λ tan(√λ) = 0
The roots of this equation give the values of λ. The roots are given by:
√λn = nπ
where n = 1, 2, 3, ...
Therefore, the values of λ are:
λn = n^2π^2
Thus, the boundary-value problem has non-zero solutions if and only if λn = n^2π^2, where n = 1, 2, 3, ...
Options
a) 0, 1, 2, ...
This option is incorrect because λ cannot be zero.
b) 1, 2, 3, ...
This option is incorrect because λ is not equal to n.
c) 1, 4, 9, ...
This option is correct because λn = n^2π^2, where n = 1, 2, 3, ...
d) 1, 9, 25, ...
This option is incorrect because the values of λ are the squares of odd integers multiplied by π^2.
Conclusion
Therefore, the correct option is c) 1, 4, 9, ... The boundary-value problem has non-zero solutions only for the values of λn = n^2π^2, where n = 1, 2, 3, ... These values are 1, 4, 9, ...
The given boundary-value problem is:
y'' + λy = 0
where y(0) = y(l) = 0
This is a second-order homogeneous differential equation with constant coefficients. The solution of this equation is given by:
y(x) = c1 sin(√λx) + c2 cos(√λx)
where c1 and c2 are constants to be determined.
Non-Zero Solutions
For non-zero solutions, the determinant of the coefficients of the homogeneous equation must be zero. This leads to the characteristic equation:
√λ tan(√λ) = 0
The roots of this equation give the values of λ. The roots are given by:
√λn = nπ
where n = 1, 2, 3, ...
Therefore, the values of λ are:
λn = n^2π^2
Thus, the boundary-value problem has non-zero solutions if and only if λn = n^2π^2, where n = 1, 2, 3, ...
Options
a) 0, 1, 2, ...
This option is incorrect because λ cannot be zero.
b) 1, 2, 3, ...
This option is incorrect because λ is not equal to n.
c) 1, 4, 9, ...
This option is correct because λn = n^2π^2, where n = 1, 2, 3, ...
d) 1, 9, 25, ...
This option is incorrect because the values of λ are the squares of odd integers multiplied by π^2.
Conclusion
Therefore, the correct option is c) 1, 4, 9, ... The boundary-value problem has non-zero solutions only for the values of λn = n^2π^2, where n = 1, 2, 3, ... These values are 1, 4, 9, ...
It is given that y" + 2y' + y = 0, y(0) = 0, y(1)=0. What is y (0.5)? - a)0
- b)0.37
- c)0.62
- d)1.13
Correct answer is option 'A'. Can you explain this answer?
It is given that y" + 2y' + y = 0, y(0) = 0, y(1)=0. What is y (0.5)?
a)
0
b)
0.37
c)
0.62
d)
1.13
|
|
Nitin Joshi answered |
Auxiliary equation is m2 + 2m +1 = 0⇒m = −1,−1
Using boundary condition y(0) = 0 and y(1) = 0
we get y = 0
we get y = 0
Chapter doubts & questions for Differential Equations - Engineering Mathematics for Mechanical Engineering 2025 is part of Mechanical Engineering exam preparation. The chapters have been prepared according to the Mechanical Engineering exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Mechanical Engineering 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Differential Equations - Engineering Mathematics for Mechanical Engineering in English & Hindi are available as part of Mechanical Engineering exam.
Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free.
Engineering Mathematics for Mechanical Engineering
53 videos|124 docs|63 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup