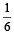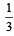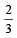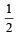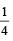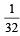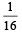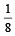All Exams >
JEE >
35 Years Chapter wise Previous Year Solved Papers for JEE >
All Questions
All questions of Probability for JEE Exam
PASSAGE - 6
Let n1 and n2 be the number of red and black balls, respectively, in box I. Let n3 and n4 be the number of red and black balls, respectively, in box II. (JEE Adv. 2015) Q. One of the two boxes, box I and box II, was selected at random and a ball was drawn randomly out of this box. The ball was found to be red. If the probability that this red ball was drawn from box II is 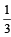 , then the correct option(s) with the possible values of n1, n2, n3 and n4 is(are)
, then the correct option(s) with the possible values of n1, n2, n3 and n4 is(are) - a)n1 = 3, n2 = 3, n3 = 5, n4 = 15
- b)n1 = 3, n2 = 6, n3 = 10, n4 = 50
- c)n1 = 8, n2 = 6, n3 = 5, n4 = 20
- d)n1 = 6, n2 = 12, n3 = 5, n4 = 20
Correct answer is option 'A,B'. Can you explain this answer?
PASSAGE - 6
Let n1 and n2 be the number of red and black balls, respectively, in box I. Let n3 and n4 be the number of red and black balls, respectively, in box II. (JEE Adv. 2015)
Let n1 and n2 be the number of red and black balls, respectively, in box I. Let n3 and n4 be the number of red and black balls, respectively, in box II. (JEE Adv. 2015)
Q. One of the two boxes, box I and box II, was selected at random and a ball was drawn randomly out of this box. The ball was found to be red. If the probability that this red ball was drawn from box II is 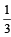 , then the correct option(s) with the possible values of n1, n2, n3 and n4 is(are)
, then the correct option(s) with the possible values of n1, n2, n3 and n4 is(are)
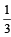 , then the correct option(s) with the possible values of n1, n2, n3 and n4 is(are)
, then the correct option(s) with the possible values of n1, n2, n3 and n4 is(are) a)
n1 = 3, n2 = 3, n3 = 5, n4 = 15
b)
n1 = 3, n2 = 6, n3 = 10, n4 = 50
c)
n1 = 8, n2 = 6, n3 = 5, n4 = 20
d)
n1 = 6, n2 = 12, n3 = 5, n4 = 20
|
|
Krishna Iyer answered |
Let E1 ≡ box I is selected
E2 ≡ box II is selected
E ≡ ball drawn is red
E2 ≡ box II is selected
E ≡ ball drawn is red
P(E2/E) = 

or 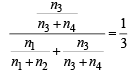
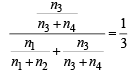
On checking the options we find (a) and (b) are the correct options.
PASSAGE - 3
Let U1 and U2 be two urns such that U1 contains 3 white and 2 red balls, and U2 contains only 1 white ball. A fair coin is tossed. If head appears then 1 ball is drawn at random from U1 and put into U2.
However, if tail appears then 2 balls are drawn at random from U1 and put into U2 . Now 1 ball is drawn at random from U2. (2011) Q. The probability of the drawn ball from U2 being white is- a)
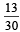
- b)
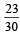
- c)
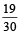
- d)
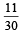
Correct answer is option 'B'. Can you explain this answer?
PASSAGE - 3
Let U1 and U2 be two urns such that U1 contains 3 white and 2 red balls, and U2 contains only 1 white ball. A fair coin is tossed. If head appears then 1 ball is drawn at random from U1 and put into U2.
However, if tail appears then 2 balls are drawn at random from U1 and put into U2 . Now 1 ball is drawn at random from U2. (2011)
Let U1 and U2 be two urns such that U1 contains 3 white and 2 red balls, and U2 contains only 1 white ball. A fair coin is tossed. If head appears then 1 ball is drawn at random from U1 and put into U2.
However, if tail appears then 2 balls are drawn at random from U1 and put into U2 . Now 1 ball is drawn at random from U2. (2011)
Q. The probability of the drawn ball from U2 being white is
a)
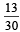
b)
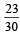
c)
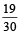
d)
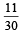

|
Om Rana answered |

A six faced fair dice is thrown until 1 comes, then the probability that 1 comes in even no. of trials is (2005S)- a)5/11
- b)5/6
- c)6/11
- d)1/6
Correct answer is option 'A'. Can you explain this answer?
A six faced fair dice is thrown until 1 comes, then the probability that 1 comes in even no. of trials is (2005S)
a)
5/11
b)
5/6
c)
6/11
d)
1/6
|
|
Krishna Iyer answered |
In single throw of a dice, probability of getting 1 is = 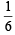 and prob. of not getting 1 is
and prob. of not getting 1 is 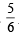
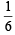 and prob. of not getting 1 is
and prob. of not getting 1 is 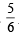
Then getting 1 in even no. of chances = getting 1 in 2nd chance or in 4th chance or in 6th chance and so on
∴ Req. Prob 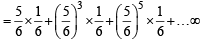
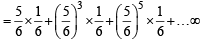
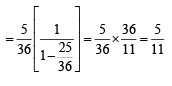
PASSAGE - 4
A box B1 contains 1 white ball, 3 red balls and 2 black balls. Another box B2 contains 2 white balls, 3 red balls and 4 black balls. A third box B3 contains 3 white balls, 4 red balls and 5 black balls. Q. If 1 ball is drawn from each of the boxes B1, B2 and B3, the probability that all 3 drawn balls are of the same colour is (JEE Adv. 2013)- a)
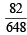
- b)
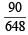
- c)

- d)
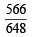
Correct answer is option 'A'. Can you explain this answer?
PASSAGE - 4
A box B1 contains 1 white ball, 3 red balls and 2 black balls. Another box B2 contains 2 white balls, 3 red balls and 4 black balls. A third box B3 contains 3 white balls, 4 red balls and 5 black balls.
A box B1 contains 1 white ball, 3 red balls and 2 black balls. Another box B2 contains 2 white balls, 3 red balls and 4 black balls. A third box B3 contains 3 white balls, 4 red balls and 5 black balls.
Q. If 1 ball is drawn from each of the boxes B1, B2 and B3, the probability that all 3 drawn balls are of the same colour is (JEE Adv. 2013)
a)
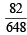
b)
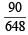
c)

d)
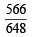
|
|
Geetika Shah answered |
Probability that all balls are of same colour = P (all red) + P (all white) + P (all black)
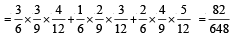
An unbiased die with faces marked 1, 2, 3, 4, 5 and 6 is rolled four times. Out of four face values obtained, the probability that the minimum face value is not less than 2 and the maximum face value is not greater than 5, is then: (1993 - 1 Mark)- a)16 / 81
- b)1 / 81
- c)80 / 81
- d)65 / 81
Correct answer is option 'A'. Can you explain this answer?
An unbiased die with faces marked 1, 2, 3, 4, 5 and 6 is rolled four times. Out of four face values obtained, the probability that the minimum face value is not less than 2 and the maximum face value is not greater than 5, is then: (1993 - 1 Mark)
a)
16 / 81
b)
1 / 81
c)
80 / 81
d)
65 / 81

|
Ankita Das answered |
Option a is correct
A pair of fair dice is thrown independently three times. The probability of getting a score of exactly 9 twice is [2007]- a)8/729
- b)8/243
- c)1/729
- d)8/9.
Correct answer is option 'B'. Can you explain this answer?
A pair of fair dice is thrown independently three times. The probability of getting a score of exactly 9 twice is [2007]
a)
8/729
b)
8/243
c)
1/729
d)
8/9.
|
|
Utkarsh Pandey answered |
Probability of getting score 9 in a single throw
=4/36
=1/9
Probability of getting score 9 exactly twice
=3C2.(1/9)^2.8/9
=8/243
Three houses are available in a locality. Three persons apply for the houses. Each applies for one house without consulting others. The probability that all the three apply for the same house is [2005]- a)
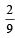
- b)
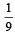
- c)
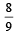
- d)
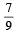
Correct answer is option 'B'. Can you explain this answer?
Three houses are available in a locality. Three persons apply for the houses. Each applies for one house without consulting others. The probability that all the three apply for the same house is [2005]
a)
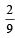
b)
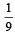
c)
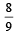
d)
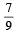
|
|
Anaya Patel answered |
For a particular house being selected Probability = 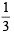
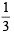
P (all the persons apply for the same house)
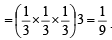
Three identical dice are rolled. The probability that the same number will appear on each of them is (1984 - 2 Marks)- a)1/6
- b)1/36
- c)1/18
- d)3/28
Correct answer is option 'B'. Can you explain this answer?
Three identical dice are rolled. The probability that the same number will appear on each of them is (1984 - 2 Marks)
a)
1/6
b)
1/36
c)
1/18
d)
3/28
|
|
Ananya Das answered |
Favourable cases = 6; {(1, 1, 1), (2, 2, 2),…(6, 6, 6)}
Total cases = 6 × 6 × 6 = 216
∴Req. prob. =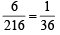
∴Req. prob. =
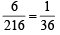
Let E and F be two independent events. The probability that exactly one of them occurs is 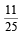 and the probability of none of them occurring is
and the probability of none of them occurring is 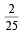 . If P(T) denotes the probability of occurrence of the event T, then (2011)
. If P(T) denotes the probability of occurrence of the event T, then (2011)- a)
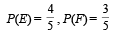
- b)
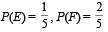
- c)
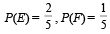
- d)

Correct answer is option 'A,D'. Can you explain this answer?
Let E and F be two independent events. The probability that exactly one of them occurs is 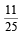 and the probability of none of them occurring is
and the probability of none of them occurring is 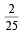 . If P(T) denotes the probability of occurrence of the event T, then (2011)
. If P(T) denotes the probability of occurrence of the event T, then (2011)
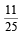 and the probability of none of them occurring is
and the probability of none of them occurring is 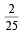 . If P(T) denotes the probability of occurrence of the event T, then (2011)
. If P(T) denotes the probability of occurrence of the event T, then (2011)a)
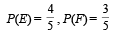
b)
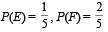
c)
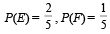
d)

|
|
Khaja Moinuddin answered |

Two aeroplanes I and II bomb a target in succession. The probabilities of I and II scoring a hit correctly are 0.3 and 0.2, respectively. The second plane will bomb only if the first misses the target. The probability that the target is hit by the second plane is [2007]- a)0.2
- b)0.7
- c)0.06
- d)0.14.
Correct answer is option 'D'. Can you explain this answer?
Two aeroplanes I and II bomb a target in succession. The probabilities of I and II scoring a hit correctly are 0.3 and 0.2, respectively. The second plane will bomb only if the first misses the target. The probability that the target is hit by the second plane is [2007]
a)
0.2
b)
0.7
c)
0.06
d)
0.14.
|
|
Athul Goyal answered |
Given : Probability of aeroplane I, scoring a target correctly i.e., P(I) = 0.3 probability of scoring a target correctly by aeroplane II, i.e. P(II) = 0.2
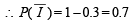 ∴ The required probability
∴ The required probability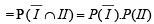 = 0.7 × 0.2 = 0.14
= 0.7 × 0.2 = 0.14 Four fair dice D1, D2, D3 and D4 ; each having six faces numbered 1, 2, 3, 4, 5 and 6 are rolled simultaneously.
The probability that D4 shows a number appearing on one of D1, D2 and D3 is (2012)- a)
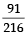
- b)
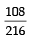
- c)
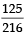
- d)
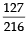
Correct answer is option 'A'. Can you explain this answer?
Four fair dice D1, D2, D3 and D4 ; each having six faces numbered 1, 2, 3, 4, 5 and 6 are rolled simultaneously.
The probability that D4 shows a number appearing on one of D1, D2 and D3 is (2012)
The probability that D4 shows a number appearing on one of D1, D2 and D3 is (2012)
a)
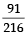
b)
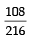
c)
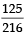
d)
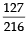
|
|
Harsh Singhal answered |
(3*6*5*5+3*6*5+6*1)/6*6*6*6
Let Ec denote the complement of an event E. Let E, F, G be pairwise independent events with P(G) > 0 and P(E∩F∩G) = 0. Then P(Ec∩ Fc| G) equals (2007 -3 marks)- a)P(Ec) + P(Fc)
- b)P(Ec) – P(Fc)
- c)P(Ec) – P(F)
- d)P(E) – P(Fc)
Correct answer is option 'C'. Can you explain this answer?
Let Ec denote the complement of an event E. Let E, F, G be pairwise independent events with P(G) > 0 and P(E∩F∩G) = 0. Then P(Ec∩ Fc| G) equals (2007 -3 marks)
a)
P(Ec) + P(Fc)
b)
P(Ec) – P(Fc)
c)
P(Ec) – P(F)
d)
P(E) – P(Fc)
|
|
Siddharth Rane answered |
P( Ec ∩ Fc /G) = P( E ∪ F )c /G) 1 - P(E∪ F /G)
= 1 - P(E / G) - P(F/ G) + P(E∩ F / G)
= 1 - P(E ) -P(F)+O
(∵ E, F, G are pairwise independent and
P(E ∩F ∩G)=0
⇒ P(E ).P(F )=0 as P(G) >0 ) = P(Ec )- P(F)
= 1 - P(E / G) - P(F/ G) + P(E∩ F / G)
= 1 - P(E ) -P(F)+O
(∵ E, F, G are pairwise independent and
P(E ∩F ∩G)=0
⇒ P(E ).P(F )=0 as P(G) >0 ) = P(Ec )- P(F)
The probability of India winning a test match against west Indies is 1/2. Assuming independence from match to match the probability that in a 5 match series India’s second win occurs at third test is (1995S)- a)1/8
- b)1/4
- c)1/2
- d)2/3
Correct answer is option 'B'. Can you explain this answer?
The probability of India winning a test match against west Indies is 1/2. Assuming independence from match to match the probability that in a 5 match series India’s second win occurs at third test is (1995S)
a)
1/8
b)
1/4
c)
1/2
d)
2/3
|
|
Kirti Datta answered |
Wins at least 3 matches can be calculated using the binomial distribution.
The binomial distribution calculates the probability of getting a certain number of successes (India winning a match) in a fixed number of independent Bernoulli trials (5 matches).
To find the probability that India wins at least 3 matches in a 5-match series, we need to calculate the probabilities of winning 3, 4, and 5 matches and then sum them up.
P(India wins at least 3 matches) = P(India wins 3 matches) + P(India wins 4 matches) + P(India wins 5 matches)
P(India wins k matches) = (5Ck) * (1/2)^k * (1/2)^(5-k)
Where (5Ck) is the binomial coefficient that represents the number of ways to choose k successes from 5 trials.
Calculating each term separately:
P(India wins 3 matches) = (5C3) * (1/2)^3 * (1/2)^(5-3) = 10 * (1/8) * (1/8) = 10/64 = 5/32
P(India wins 4 matches) = (5C4) * (1/2)^4 * (1/2)^(5-4) = 5 * (1/16) * (1/2) = 5/32
P(India wins 5 matches) = (5C5) * (1/2)^5 * (1/2)^(5-5) = 1 * (1/32) * (1/1) = 1/32
Now, summing up the probabilities:
P(India wins at least 3 matches) = 5/32 + 5/32 + 1/32 = 11/32
Therefore, the probability that India wins at least 3 matches in a 5-match series against West Indies is 11/32.
The binomial distribution calculates the probability of getting a certain number of successes (India winning a match) in a fixed number of independent Bernoulli trials (5 matches).
To find the probability that India wins at least 3 matches in a 5-match series, we need to calculate the probabilities of winning 3, 4, and 5 matches and then sum them up.
P(India wins at least 3 matches) = P(India wins 3 matches) + P(India wins 4 matches) + P(India wins 5 matches)
P(India wins k matches) = (5Ck) * (1/2)^k * (1/2)^(5-k)
Where (5Ck) is the binomial coefficient that represents the number of ways to choose k successes from 5 trials.
Calculating each term separately:
P(India wins 3 matches) = (5C3) * (1/2)^3 * (1/2)^(5-3) = 10 * (1/8) * (1/8) = 10/64 = 5/32
P(India wins 4 matches) = (5C4) * (1/2)^4 * (1/2)^(5-4) = 5 * (1/16) * (1/2) = 5/32
P(India wins 5 matches) = (5C5) * (1/2)^5 * (1/2)^(5-5) = 1 * (1/32) * (1/1) = 1/32
Now, summing up the probabilities:
P(India wins at least 3 matches) = 5/32 + 5/32 + 1/32 = 11/32
Therefore, the probability that India wins at least 3 matches in a 5-match series against West Indies is 11/32.
An experiment has 10 equally likely outcomes. Let A and B be non-empty events of the experiment. If A consists of 4 outcomes, the number of outcomes that B must have so that A and B are independent, is (2008)- a)2, 4 or 8
- b)3, 6 or 9
- c)4 or 8
- d)5 or 10
Correct answer is option 'D'. Can you explain this answer?
An experiment has 10 equally likely outcomes. Let A and B be non-empty events of the experiment. If A consists of 4 outcomes, the number of outcomes that B must have so that A and B are independent, is (2008)
a)
2, 4 or 8
b)
3, 6 or 9
c)
4 or 8
d)
5 or 10
|
|
Shreya Dasgupta answered |
We have n (S) = 10, n(A) = 4
Let n(B) = x and n(A ∩ B) = y
Then for A and B to be independent events P(A ∩ B) = P(A) P(B)
Let n(B) = x and n(A ∩ B) = y
Then for A and B to be independent events P(A ∩ B) = P(A) P(B)
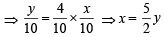
⇒ y can be 2 or 4 so that x = 5 or 10
∴ n (B) = 5 or 10
∴ n (B) = 5 or 10
The probabilities that a student passes in Mathematics, Physics and Chemistry are m, p and c, respectively. Of these subjects, the student has a 75% chance of passing in at least one, a 50% chance of passing in at least two, and a 40% chance of passing in exactly two. Which of the following relations are true? (1999 - 3 Marks)- a)p + m + c = 19/20
- b)p + m + c = 27/20
- c)pmc = 1/10
- d)pmc = 1/4
Correct answer is option 'B,C'. Can you explain this answer?
The probabilities that a student passes in Mathematics, Physics and Chemistry are m, p and c, respectively. Of these subjects, the student has a 75% chance of passing in at least one, a 50% chance of passing in at least two, and a 40% chance of passing in exactly two. Which of the following relations are true? (1999 - 3 Marks)
a)
p + m + c = 19/20
b)
p + m + c = 27/20
c)
pmc = 1/10
d)
pmc = 1/4
|
|
Arka Yadav answered |
According to the problem, m + p + c – mp – mc – pc + mpc = 3/4 …(1)
mp (1– c) + mc (1– p) + pc (1– m) = 2/5 or mp + mc + pc – 3mpc = 2/5 … (2)
Also mp + pc + mc – 2mpc = 1/2 … (3)
mp (1– c) + mc (1– p) + pc (1– m) = 2/5 or mp + mc + pc – 3mpc = 2/5 … (2)
Also mp + pc + mc – 2mpc = 1/2 … (3)
(2) and (3) ⇒ 
∴ mp + mc + pc = 

∴ m + p + c =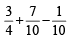
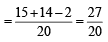
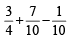
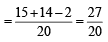
Two fair dice are tossed. Let x be the event that the first die shows an even number and y be the event that the second die shows an odd number. The two events x and y are :- a)Mutually exclusive (1979)
- b)Independent and mutually exclusive
- c)Dependent
- d)None of these.
Correct answer is option 'D'. Can you explain this answer?
Two fair dice are tossed. Let x be the event that the first die shows an even number and y be the event that the second die shows an odd number. The two events x and y are :
a)
Mutually exclusive (1979)
b)
Independent and mutually exclusive
c)
Dependent
d)
None of these.
|
|
Shalini Yadav answered |
Explanation:
Mutually Exclusive Events:
- Two events are mutually exclusive if they cannot occur at the same time.
- In this case, event x (the first die showing an even number) and event y (the second die showing an odd number) can both occur simultaneously.
- Therefore, x and y are not mutually exclusive.
Independent Events:
- Two events are independent if the occurrence of one event does not affect the occurrence of the other event.
- In this case, the outcome of the first die does not affect the outcome of the second die, so x and y are independent events.
Dependent Events:
- Two events are dependent if the occurrence of one event affects the occurrence of the other event.
- In this case, the outcome of the first die could potentially influence the outcome of the second die (for example, if the first die shows a 6, the probability of the second die being odd changes).
- Therefore, x and y are dependent events.
Conclusion:
- Since the events x and y are not mutually exclusive and are dependent on each other, the correct answer is option 'D' - None of these.
Mutually Exclusive Events:
- Two events are mutually exclusive if they cannot occur at the same time.
- In this case, event x (the first die showing an even number) and event y (the second die showing an odd number) can both occur simultaneously.
- Therefore, x and y are not mutually exclusive.
Independent Events:
- Two events are independent if the occurrence of one event does not affect the occurrence of the other event.
- In this case, the outcome of the first die does not affect the outcome of the second die, so x and y are independent events.
Dependent Events:
- Two events are dependent if the occurrence of one event affects the occurrence of the other event.
- In this case, the outcome of the first die could potentially influence the outcome of the second die (for example, if the first die shows a 6, the probability of the second die being odd changes).
- Therefore, x and y are dependent events.
Conclusion:
- Since the events x and y are not mutually exclusive and are dependent on each other, the correct answer is option 'D' - None of these.
A dice is tossed 5 times. Getting an odd number is considered a success. Then the variance of distribution of success is [2002]- a)8/3
- b)3/8
- c)4/5
- d)5/4
Correct answer is option 'D'. Can you explain this answer?
A dice is tossed 5 times. Getting an odd number is considered a success. Then the variance of distribution of success is [2002]
a)
8/3
b)
3/8
c)
4/5
d)
5/4
|
|
Pragati Saha answered |
The event follows binomial distribution with
n = 5, p = 3/6 = 1/2. q = 1 – p = 1/2.;
∴ Variance = npq = 5/4.
n = 5, p = 3/6 = 1/2. q = 1 – p = 1/2.;
∴ Variance = npq = 5/4.
Let ω be a complex cube root of unity with ω ≠ 1. A fair die is thrown three times. If r1, r2 and r3 are the numbers obtained on the die, then the probability that ωr1 + ωr2 + ωr3 = 0 is (2010)- a)
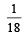
- b)
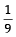
- c)
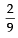
- d)
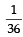
Correct answer is option 'C'. Can you explain this answer?
Let ω be a complex cube root of unity with ω ≠ 1. A fair die is thrown three times. If r1, r2 and r3 are the numbers obtained on the die, then the probability that ωr1 + ωr2 + ωr3 = 0 is (2010)
a)
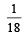
b)
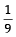
c)
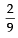
d)
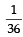
|
|
Chirag Verma answered |
If ω is a complex cube root of unity then, we know that ω3m +ω3n+1 +ω3p +2 = 0 where m, n, p are integers.
∴ r1, r2, r3 should be of the form 3m, 3n + 1 and 3p + 2 taken in any or d er. As r1 ,r2 ,r3 are the numbers obtained on die, these can take any value from 1 to 6.
∴ m can take values 1 or 2, n can take values 0 or 1p can take values 0 or 1
∴ Number of ways of selecting r1, r2, r3
= 2C1 x 2C1 x 2C1 x 3!.
Also the total number of ways of getting r1, r2, r3 on die = 6 × 6 × 6
∴ r1, r2, r3 should be of the form 3m, 3n + 1 and 3p + 2 taken in any or d er. As r1 ,r2 ,r3 are the numbers obtained on die, these can take any value from 1 to 6.
∴ m can take values 1 or 2, n can take values 0 or 1p can take values 0 or 1
∴ Number of ways of selecting r1, r2, r3
= 2C1 x 2C1 x 2C1 x 3!.
Also the total number of ways of getting r1, r2, r3 on die = 6 × 6 × 6
∴ Required probability=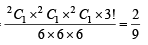
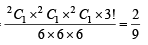
The probability that an event A happens in one trial of an experiment is 0.4. Three independent trials of the experiment are performed. The probability that the event A happens at least once is (1980)- a)0.936
- b)0.784
- c)0.904
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
The probability that an event A happens in one trial of an experiment is 0.4. Three independent trials of the experiment are performed. The probability that the event A happens at least once is (1980)
a)
0.936
b)
0.784
c)
0.904
d)
none of these
|
|
Rishika Roy answered |
p = 0.4, n = 3, P (X ≥ 1) = ? ⇒ q = 0.6
∴ P (X ≥ 1) = 1– P (X = 0)
= 1– 3C0(0.4)0 (0.6)3 = 1 – 0.216 = 0.784
∴ P (X ≥ 1) = 1– P (X = 0)
= 1– 3C0(0.4)0 (0.6)3 = 1 – 0.216 = 0.784
Two numbers are selected randomly from the set S = {1, 2, 3, 4, 5, 6} without replacement one by one. The probability that minimum of the two numbers is less than 4 is (2003S)- a)1/15
- b)14/15
- c)1/5
- d)4/5
Correct answer is option 'D'. Can you explain this answer?
Two numbers are selected randomly from the set S = {1, 2, 3, 4, 5, 6} without replacement one by one. The probability that minimum of the two numbers is less than 4 is (2003S)
a)
1/15
b)
14/15
c)
1/5
d)
4/5
|
|
Akash Das answered |
The minimum of two numbers will be less than 4 if at least one of the numbers is less than 4.
∴ P (at least one no. is < 4), = 1– P (both the no’s are ≥ 4)
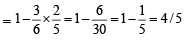
One hundred identical coins, each with probability, p, of showing up heads are tossed once. If 0 < p < 1 and the probabilitity of heads showing on 50 coins is equal to that of heads showing on 51 coins, then the value of p is (1988 - 2 Marks)- a)1/2
- b)49/101
- c)50/101
- d)51/101.
Correct answer is option 'D'. Can you explain this answer?
One hundred identical coins, each with probability, p, of showing up heads are tossed once. If 0 < p < 1 and the probabilitity of heads showing on 50 coins is equal to that of heads showing on 51 coins, then the value of p is (1988 - 2 Marks)
a)
1/2
b)
49/101
c)
50/101
d)
51/101.
|
|
Ameya Das answered |
Understanding the Problem
We are tossing 100 identical coins, each with a head probability of p. We need to find p such that the probability of getting 50 heads is equal to the probability of getting 51 heads.
Probability Formulation
The probability of getting k heads in n tosses of coins is given by:
P(k) = C(n, k) * p^k * (1-p)^(n-k)
Where C(n, k) is the combination of n items taken k at a time.
For our problem, we have:
- P(50) = C(100, 50) * p^50 * (1-p)^50
- P(51) = C(100, 51) * p^51 * (1-p)^49
Setting Up the Equation
To find p, we set P(50) = P(51):
C(100, 50) * p^50 * (1-p)^50 = C(100, 51) * p^51 * (1-p)^49
Simplifying the Equation
We can simplify this equation:
C(100, 51) = C(100, 50) * (100 - 51) / (51)
This gives us:
p / (1-p) = 49/51
Solving for p
Rearranging the equation, we find:
p = (49/51) * (1 - p)
This leads to:
p + (49/51)p = 49/51
Now, we can calculate p:
(100/51)p = 49/51
Thus, we find:
p = 49/100 + 2/100 = 51/101
Conclusion
The value of p that satisfies the condition is:
Hence, the correct answer is option 'D'.
We are tossing 100 identical coins, each with a head probability of p. We need to find p such that the probability of getting 50 heads is equal to the probability of getting 51 heads.
Probability Formulation
The probability of getting k heads in n tosses of coins is given by:
P(k) = C(n, k) * p^k * (1-p)^(n-k)
Where C(n, k) is the combination of n items taken k at a time.
For our problem, we have:
- P(50) = C(100, 50) * p^50 * (1-p)^50
- P(51) = C(100, 51) * p^51 * (1-p)^49
Setting Up the Equation
To find p, we set P(50) = P(51):
C(100, 50) * p^50 * (1-p)^50 = C(100, 51) * p^51 * (1-p)^49
Simplifying the Equation
We can simplify this equation:
C(100, 51) = C(100, 50) * (100 - 51) / (51)
This gives us:
p / (1-p) = 49/51
Solving for p
Rearranging the equation, we find:
p = (49/51) * (1 - p)
This leads to:
p + (49/51)p = 49/51
Now, we can calculate p:
(100/51)p = 49/51
Thus, we find:
p = 49/100 + 2/100 = 51/101
Conclusion
The value of p that satisfies the condition is:
p = 51/101
Hence, the correct answer is option 'D'.
If from each of the three boxes containing 3 white and 1 black, 2 white and 2 black, 1 white and 3 black balls, one ball is drawn at random, then the probability that 2 white and 1 black ball will be drawn is (1998 - 2 Marks)- a)13/32
- b)1/4
- c)1/32
- d)3/16
Correct answer is option 'A'. Can you explain this answer?
If from each of the three boxes containing 3 white and 1 black, 2 white and 2 black, 1 white and 3 black balls, one ball is drawn at random, then the probability that 2 white and 1 black ball will be drawn is (1998 - 2 Marks)
a)
13/32
b)
1/4
c)
1/32
d)
3/16
|
|
Ritika Sen answered |
P (2 white and 1 black) = P (W1 W2 B3 or W1 B2 W3 or B1 W2 W3)
= P (W1 W2 B3) + P (W1 B2 W3) + P (B1 W2 W3)
= P (W1) P(W2) P (B3) + P (W1) P(B2) P (W3)
+ P (B1) P (W2) P (W3)
= P (W1 W2 B3) + P (W1 B2 W3) + P (B1 W2 W3)
= P (W1) P(W2) P (B3) + P (W1) P(B2) P (W3)
+ P (B1) P (W2) P (W3)
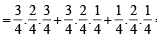
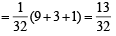
PASSAGE - 1There are n urns, each of these contain n + 1 balls. The ith urn contains i white balls and (n + 1 – i) red balls. Let ui be the event of selecting ith urn, i = 1, 2, 3 .........., n and w the event of getting a white ball.Q. If P(ui) ∝ i, where i = 1, 2, 3,......., n, then  P(w) =(2006 - 5M, –2)
P(w) =(2006 - 5M, –2)- a)1
- b)2/3
- c)3/4
- d)1/4
Correct answer is option 'B'. Can you explain this answer?
PASSAGE - 1
There are n urns, each of these contain n + 1 balls. The ith urn contains i white balls and (n + 1 – i) red balls. Let ui be the event of selecting ith urn, i = 1, 2, 3 .........., n and w the event of getting a white ball.
Q. If P(ui) ∝ i, where i = 1, 2, 3,......., n, then 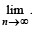 P(w) =(2006 - 5M, –2)
P(w) =(2006 - 5M, –2)
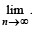 P(w) =(2006 - 5M, –2)
P(w) =(2006 - 5M, –2)a)
1
b)
2/3
c)
3/4
d)
1/4
|
|
Vandana Roy answered |
P(ui) ∝ i ⇒ P(ui)= ki, But ∑ P(ui)=1
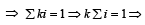
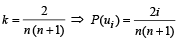
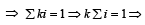
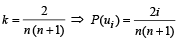
By total prob. theorem
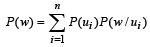
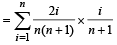
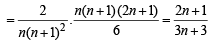
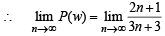
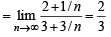
If 12 identical balls are to be placed in 3 identical boxes, then the probability that one of the boxes contains exactly 3 balls is : [JEE M 2015]- a)
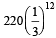
- b)
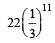
- c)
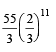
- d)
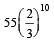
Correct answer is option 'C'. Can you explain this answer?
If 12 identical balls are to be placed in 3 identical boxes, then the probability that one of the boxes contains exactly 3 balls is : [JEE M 2015]
a)
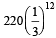
b)
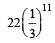
c)
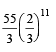
d)
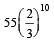
|
|
Palak Gupta answered |
Note:- The question should state ‘3 different’ boxes instead of ‘3 identical boxes’ and one particular box has 3 balls. Then the solution would be:
Required probability =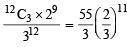
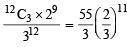
If the integers m and n are chosen at random from 1 to 100, then the probability that a number of the form 7m + 7n is divisible by 5 equals (1999 - 2 Marks)- a)1/4
- b)1/7
- c)1/8
- d)1/49
Correct answer is option 'A'. Can you explain this answer?
If the integers m and n are chosen at random from 1 to 100, then the probability that a number of the form 7m + 7n is divisible by 5 equals (1999 - 2 Marks)
a)
1/4
b)
1/7
c)
1/8
d)
1/49
|
|
Janani Pillai answered |
We know that, 71= 7, 72 = 49, 73 = 343, 74 = 2401, 75 = 16807
∴ 7k (where k ∈ Z), results in a number whose unit’ss digit is 7 or 9 or 3 or 1.
Now, 7m + 7n will be divisible by 5 if unit’s place digit of resulting number is 5 or 0 clearly it can never be 5.
But it can be 0 if we consider values of m and n such that the sum of unit’s place digits become 0. And this can be done by choosing
∴ 7k (where k ∈ Z), results in a number whose unit’ss digit is 7 or 9 or 3 or 1.
Now, 7m + 7n will be divisible by 5 if unit’s place digit of resulting number is 5 or 0 clearly it can never be 5.
But it can be 0 if we consider values of m and n such that the sum of unit’s place digits become 0. And this can be done by choosing
 (25 options each) [7 + 3 = 10]
(25 options each) [7 + 3 = 10] (25 options each) [9 + 1= 10]
(25 options each) [9 + 1= 10]Case I : Thus m can be chosen in 25 ways and n can be chosen in 25 ways
Case II : m can be chosen in 25 ways and n can be chosen in 25 ways
∴ Total no. of selections of m, n so that 7m + 7n is divisible by 5 = (25 × 25 + 25 × 25 ) × 2
Note we can interchange values of m and n.
Also no. of total possible selections of m and n out of 100 = 100 × 100
Also no. of total possible selections of m and n out of 100 = 100 × 100
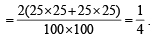
For the three events A, B, and C, P (exactly one of the events A or B occurs) = P (exactly one of the two events B or C occurs) = P(exactly one of the events C or A occurs) = p and P (all the three events occur simultaneously) = p2, where 0 < p < 1/2. Then the probability of at least one of the three events A, B and C occurring is (1996 - 2 Marks)- a)
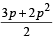
- b)
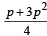
- c)
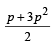
- d)
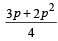
Correct answer is option 'A'. Can you explain this answer?
For the three events A, B, and C, P (exactly one of the events A or B occurs) = P (exactly one of the two events B or C occurs) = P(exactly one of the events C or A occurs) = p and P (all the three events occur simultaneously) = p2, where 0 < p < 1/2. Then the probability of at least one of the three events A, B and C occurring is (1996 - 2 Marks)
a)
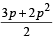
b)
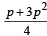
c)
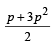
d)
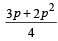
|
|
Disha Kaur answered |
We know that P (exactly one of A or B occurs) = P (A) + P (B) – 2P (A ∩ B).
Therefore, P (A) + P (B) – 2P (A ∩ B) = p … (1)
Similarly, P (B) + P (C) – 2P (B ∩ C) = p … (2)
and P (C) + P (A) – 2P (C ∩ A) = p …(3)
Adding (1), (2) and (3) we get 2 [P (A) + P (B) + P (C) – P (A ∩ B)
– P (B ∩ C) – P (C ∩ A)] = 3p ⇒ P (A) + P (B) + P (C) – P (A ∩ B)
– P (B ∩ C) – P (C ∩ A) = 3p/2 … (4)
We are also given that, P (A ∩ B ∩ C) = p2 … (5)
Now, P (at least one of A, B and C) = P (A) + P (B) + P (C) – P (A ∩ B) – P (B ∩ C)
– P (C ∩ A) + P (A ∩ B ∩ C)
Therefore, P (A) + P (B) – 2P (A ∩ B) = p … (1)
Similarly, P (B) + P (C) – 2P (B ∩ C) = p … (2)
and P (C) + P (A) – 2P (C ∩ A) = p …(3)
Adding (1), (2) and (3) we get 2 [P (A) + P (B) + P (C) – P (A ∩ B)
– P (B ∩ C) – P (C ∩ A)] = 3p ⇒ P (A) + P (B) + P (C) – P (A ∩ B)
– P (B ∩ C) – P (C ∩ A) = 3p/2 … (4)
We are also given that, P (A ∩ B ∩ C) = p2 … (5)
Now, P (at least one of A, B and C) = P (A) + P (B) + P (C) – P (A ∩ B) – P (B ∩ C)
– P (C ∩ A) + P (A ∩ B ∩ C)
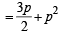 [using (4) and (5)]
[using (4) and (5)] 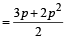
In dia plays two matches each with West In dies and Australia. In any match the probabilities of India getting, points 0, 1 and 2 are 0.45, 0.05 and 0.50 respectively.Assuming that the outcomes are independent, the probability of India getting at least 7 points is (1992 - 2 Marks)- a)0.8750
- b)0.0875
- c)0.0625
- d)0.0250
Correct answer is option 'B'. Can you explain this answer?
In dia plays two matches each with West In dies and Australia. In any match the probabilities of India getting, points 0, 1 and 2 are 0.45, 0.05 and 0.50 respectively.Assuming that the outcomes are independent, the probability of India getting at least 7 points is (1992 - 2 Marks)
a)
0.8750
b)
0.0875
c)
0.0625
d)
0.0250
|
|
Pallabi Basak answered |
P (at least 7 pts) = P (7pts) + P (8 pts) [∵ At most 8 pts can be scored.]
Now 7 pts can be scored by scoring 2 pts in 3 matches and 1 pt. in one match, similarly 8 pts can be scored by scoring 2 pts in each of the 4 matches.
∴ Req. prob. = 4C1 × [P (2 pts)]3 P (1pt) + [P (2 pts)]4 = 4 (0.5)3 × 0.05 + (0.50)4 = 0.0250 + 0.0625 = 0.0875
Now 7 pts can be scored by scoring 2 pts in 3 matches and 1 pt. in one match, similarly 8 pts can be scored by scoring 2 pts in each of the 4 matches.
∴ Req. prob. = 4C1 × [P (2 pts)]3 P (1pt) + [P (2 pts)]4 = 4 (0.5)3 × 0.05 + (0.50)4 = 0.0250 + 0.0625 = 0.0875
If E and F are independent events such that 0 < P(E) <1 and 0 < P(F) < 1, then (1989 - 2 Marks)- a)E and F are mutually exclusive
- b)E and Fc ( the complement of the event F) are independent
- c)Ec and Fc are independent
- d)P(E | F) + P(Ec | F) = 1.
Correct answer is option 'B,C,D'. Can you explain this answer?
If E and F are independent events such that 0 < P(E) <1 and 0 < P(F) < 1, then (1989 - 2 Marks)
a)
E and F are mutually exclusive
b)
E and Fc ( the complement of the event F) are independent
c)
Ec and Fc are independent
d)
P(E | F) + P(Ec | F) = 1.
|
|
Sanchita Chavan answered |
Since E and F are independent
∴ P (E ∩ F) = P (E) . P ( F) ...(1)
Now, P (E ∩ Fc) = P (E) – P (E ∩ F) = P (E) – P(E) P(F) [Using (1)]
= P (E) [1 – P (F)] = P (E) P (Fc)
∴ E and Fc are independent.
Again P (Ec ∩ Fc) = P (E ∪ F)c = 1 – P (E ∪ F) = 1– P (E) – P (F) + P (E ∩ F)
= 1 – P (E) – P (F) + P (E) P (F)
= ((1– P (E) (1 – P (F)) = P (Ec) P (Fc)
∴ Ec and Fc are independent.
Also P (E/ F) + P (Ec/F)
∴ P (E ∩ F) = P (E) . P ( F) ...(1)
Now, P (E ∩ Fc) = P (E) – P (E ∩ F) = P (E) – P(E) P(F) [Using (1)]
= P (E) [1 – P (F)] = P (E) P (Fc)
∴ E and Fc are independent.
Again P (Ec ∩ Fc) = P (E ∪ F)c = 1 – P (E ∪ F) = 1– P (E) – P (F) + P (E ∩ F)
= 1 – P (E) – P (F) + P (E) P (F)
= ((1– P (E) (1 – P (F)) = P (Ec) P (Fc)
∴ Ec and Fc are independent.
Also P (E/ F) + P (Ec/F)
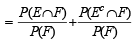
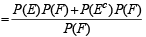
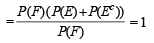
If 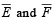 are the complementary events of events E and F respectively and if 0 < P(F) < 1, then (1998 - 2 Marks)
are the complementary events of events E and F respectively and if 0 < P(F) < 1, then (1998 - 2 Marks)- a)
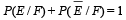
- b)
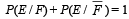
- c)
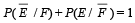
- d)
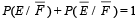
Correct answer is option 'A,D'. Can you explain this answer?
If 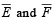 are the complementary events of events E and F respectively and if 0 < P(F) < 1, then (1998 - 2 Marks)
are the complementary events of events E and F respectively and if 0 < P(F) < 1, then (1998 - 2 Marks)
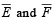 are the complementary events of events E and F respectively and if 0 < P(F) < 1, then (1998 - 2 Marks)
are the complementary events of events E and F respectively and if 0 < P(F) < 1, then (1998 - 2 Marks)a)
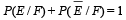
b)
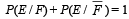
c)
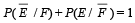
d)
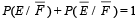
|
|
Siddharth Basak answered |
We have,
(a) 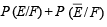
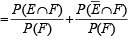
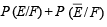
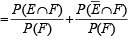
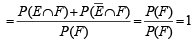
∴ (a) holds.
Also
Also
(b) 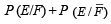
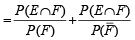
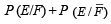
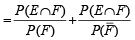
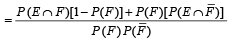
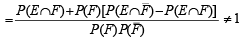
∴ (b) does not hold. Similarly we can show that (c) does not hold but (d) holds.
A fair coin is tossed repeatedly. If the tail appears on first four tosses, then the probability of the head appearing on the fifth toss equals (1998 - 2 Marks)- a)1/2
- b)1/32
- c)31/32
- d)1/5
Correct answer is option 'A'. Can you explain this answer?
A fair coin is tossed repeatedly. If the tail appears on first four tosses, then the probability of the head appearing on the fifth toss equals (1998 - 2 Marks)
a)
1/2
b)
1/32
c)
31/32
d)
1/5
|
|
Nandita Sharma answered |
Th e even t that th e fifth toss r esults in a h ead is independent of the event that the first four tosses result in tails.
∴ Probability of the required event = 1/2.
∴ Probability of the required event = 1/2.
A random variable X has Poisson distribution with mean 2.
Then P (X > 1.5) equals [2005]- a)
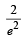
- b)0
- c)
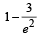
- d)
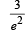
Correct answer is option 'C'. Can you explain this answer?
A random variable X has Poisson distribution with mean 2.
Then P (X > 1.5) equals [2005]
Then P (X > 1.5) equals [2005]
a)
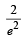
b)
0
c)
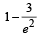
d)
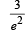
|
|
Devanshi Bajaj answered |
According to Poission distribution, prob. of getting k successes is
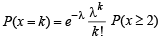 =1- P(x = 0) - P(x=1)
=1- P(x = 0) - P(x=1)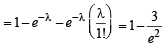
PASSAGE - 5
Box 1 contains three cards bearing numbers 1, 2, 3; box 2 contains five cards bearing numbers 1, 2, 3, 4, 5; and box 3 contains seven cards bearing numbers 1, 2, 3, 4, 5, 6, 7. A card is drawn from each of the boxes. Let xi be number on the card drawn from the ith box, i = 1, 2, 3. (JEE Adv. 2014) Q. The probability that x1 + x2 + x3 is odd, is- a)
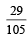
- b)
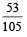
- c)
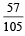
- d)
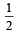
Correct answer is option 'B'. Can you explain this answer?
PASSAGE - 5
Box 1 contains three cards bearing numbers 1, 2, 3; box 2 contains five cards bearing numbers 1, 2, 3, 4, 5; and box 3 contains seven cards bearing numbers 1, 2, 3, 4, 5, 6, 7. A card is drawn from each of the boxes. Let xi be number on the card drawn from the ith box, i = 1, 2, 3. (JEE Adv. 2014)
Box 1 contains three cards bearing numbers 1, 2, 3; box 2 contains five cards bearing numbers 1, 2, 3, 4, 5; and box 3 contains seven cards bearing numbers 1, 2, 3, 4, 5, 6, 7. A card is drawn from each of the boxes. Let xi be number on the card drawn from the ith box, i = 1, 2, 3. (JEE Adv. 2014)
Q. The probability that x1 + x2 + x3 is odd, is
a)
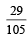
b)
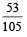
c)
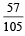
d)
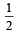
|
|
Sparsh Roy answered |
x1 + x2 + x3 will be odd If two are even and one is odd or all three are odd.
∴ Required probability = P (EEO) + P(EOE) + P(OEE) + P(OQO)
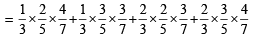
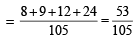
Four numbers are chosen at random (without replacement) from the set {1, 2, 3, ...20}. [2010]Statement -1: The probability that the chosen numbers when arranged in some order will form an AP is 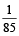 Statement -2 : If the four chosen numbers form an AP, then the set of all possible values of common difference is (±1, ±2, ±3, ±4,±5) .
Statement -2 : If the four chosen numbers form an AP, then the set of all possible values of common difference is (±1, ±2, ±3, ±4,±5) . - a)Statement -1 is true, Statement -2 is true ; Statement -2 is not a correct explanation for Statement -1
- b)Statement -1 is true, Statment -2 is false
- c)Statement -1 is false, Statment -2 is true.
- d)Statement -1 is true, Statement -2 is true ; Statement -2 is a correct explanation for Statement -1.
Correct answer is option 'B'. Can you explain this answer?
Four numbers are chosen at random (without replacement) from the set {1, 2, 3, ...20}. [2010]
Statement -1: The probability that the chosen numbers when arranged in some order will form an AP is 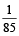
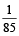
Statement -2 : If the four chosen numbers form an AP, then the set of all possible values of common difference is (±1, ±2, ±3, ±4,±5) .
a)
Statement -1 is true, Statement -2 is true ; Statement -2 is not a correct explanation for Statement -1
b)
Statement -1 is true, Statment -2 is false
c)
Statement -1 is false, Statment -2 is true.
d)
Statement -1 is true, Statement -2 is true ; Statement -2 is a correct explanation for Statement -1.
|
|
Bibek Joshi answered |
n(S) = 20C4 Statement-1:
common difference is 1; total number of cases = 17
common difference is 2; total number of cases = 14
common difference is 3; total number of cases = 11
common difference is 4; total number of cases = 8
common difference is 5; total number of cases = 5
common difference is 6; total number of cases = 2
common difference is 1; total number of cases = 17
common difference is 2; total number of cases = 14
common difference is 3; total number of cases = 11
common difference is 4; total number of cases = 8
common difference is 5; total number of cases = 5
common difference is 6; total number of cases = 2
Prob. = 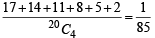
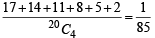
Statement -2 is false, because common difference can be 6 also.
PASSAGE - 1There are n urns, each of these contain n + 1 balls. The ith urn contains i white balls and (n + 1 – i) red balls. Let ui be the event of selecting ith urn, i = 1, 2, 3 .........., n and w the event of getting a white ball.Q. If P(ui) = c, (a constant) then P(un/w) = (2006 - 5M, –2)- a)
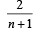
- b)
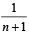
- c)
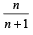
- d)
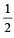
Correct answer is option 'A'. Can you explain this answer?
PASSAGE - 1
There are n urns, each of these contain n + 1 balls. The ith urn contains i white balls and (n + 1 – i) red balls. Let ui be the event of selecting ith urn, i = 1, 2, 3 .........., n and w the event of getting a white ball.
Q. If P(ui) = c, (a constant) then P(un/w) = (2006 - 5M, –2)
a)
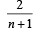
b)
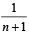
c)
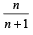
d)
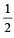
|
|
Mahi Reddy answered |
P(ui) = c
Using Baye’s theorem,
Using Baye’s theorem,
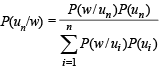
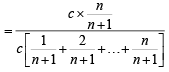
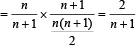
PASSAGE - 3
Let U1 and U2 be two urns such that U1 contains 3 white and 2 red balls, and U2 contains only 1 white ball. A fair coin is tossed. If head appears then 1 ball is drawn at random from U1 and put into U2.
However, if tail appears then 2 balls are drawn at random from U1 and put into U2 . Now 1 ball is drawn at random from U2. (2011) Q. Given that the drawn ball from U2 is white, the probability that head appeared on the coin is- a)
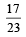
- b)
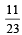
- c)
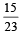
- d)
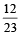
Correct answer is option 'D'. Can you explain this answer?
PASSAGE - 3
Let U1 and U2 be two urns such that U1 contains 3 white and 2 red balls, and U2 contains only 1 white ball. A fair coin is tossed. If head appears then 1 ball is drawn at random from U1 and put into U2.
However, if tail appears then 2 balls are drawn at random from U1 and put into U2 . Now 1 ball is drawn at random from U2. (2011)
Let U1 and U2 be two urns such that U1 contains 3 white and 2 red balls, and U2 contains only 1 white ball. A fair coin is tossed. If head appears then 1 ball is drawn at random from U1 and put into U2.
However, if tail appears then 2 balls are drawn at random from U1 and put into U2 . Now 1 ball is drawn at random from U2. (2011)
Q. Given that the drawn ball from U2 is white, the probability that head appeared on the coin is
a)
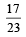
b)
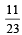
c)
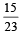
d)
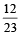
|
|
Gaurav Rane answered |
P(H/white) =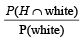
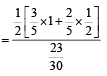
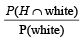
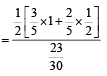
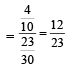
Con sid er 5 in dependen t Ber n oull i’s tr i als each wi th probability of success p. If the probability of at least one failure is greater than or equal to 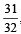 then p lies in the interval [2011]
then p lies in the interval [2011]- a)
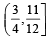
- b)
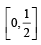
- c)
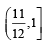
- d)
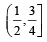
Correct answer is option 'B'. Can you explain this answer?
Con sid er 5 in dependen t Ber n oull i’s tr i als each wi th probability of success p. If the probability of at least one failure is greater than or equal to 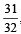 then p lies in the interval [2011]
then p lies in the interval [2011]
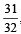 then p lies in the interval [2011]
then p lies in the interval [2011]a)
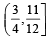
b)
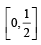
c)
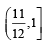
d)
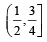
|
|
Bhavya Tiwari answered |
p (at least one failure) 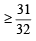
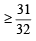
⇒ 1 – p (no failure) 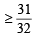
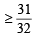
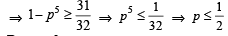
But p ≥ 0,
Hence p lies in the interval 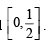
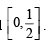
The probability that A speaks truth is , 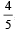 while the probability for B is .
while the probability for B is . 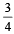
The probability that they contradicteach oth er when asked to speak on a fact is [2004]- a)
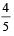
- b)
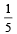
- c)
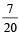
- d)
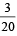
Correct answer is option 'C'. Can you explain this answer?
The probability that A speaks truth is , 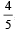 while the probability for B is .
while the probability for B is . 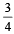
The probability that they contradicteach oth er when asked to speak on a fact is [2004]
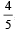 while the probability for B is .
while the probability for B is . 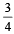
The probability that they contradicteach oth er when asked to speak on a fact is [2004]
a)
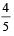
b)
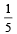
c)
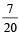
d)
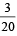
|
|
Shreya Sengupta answered |
A an d B will contradict each other if one speaks truth and other false . So , the required
Probability = 

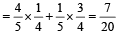
A and B are events such that P(A ∪ B)=3/4, P(A ∩ B)=1/4,  is [2002]
is [2002]- a)5/12
- b)3/8
- c)5/8
- d)1/4
Correct answer is option 'A'. Can you explain this answer?
A and B are events such that P(A ∪ B)=3/4, P(A ∩ B)=1/4,  is [2002]
is [2002]
 is [2002]
is [2002]a)
5/12
b)
3/8
c)
5/8
d)
1/4
|
|
Palak Banerjee answered |
P (A ∪ B) = P (A) + P (B) – P (A ∩ B);
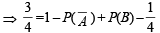
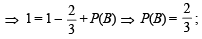
Now, 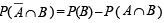
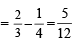
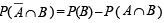
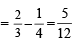
Let A and B be two events such that 
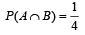 and
and 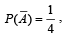 where
where 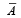 stands forcomplement of event A. Then events A and B are
stands forcomplement of event A. Then events A and B are- a)equally likely and mutually exclusive [2005]
- b)equally likely but not independent
- c)independent but not equally likely
- d)mutually exclusive and independent
Correct answer is option 'C'. Can you explain this answer?
Let A and B be two events such that 
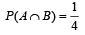 and
and 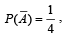 where
where 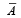 stands forcomplement of event A. Then events A and B are
stands forcomplement of event A. Then events A and B are

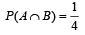 and
and 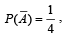 where
where 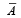 stands forcomplement of event A. Then events A and B are
stands forcomplement of event A. Then events A and B area)
equally likely and mutually exclusive [2005]
b)
equally likely but not independent
c)
independent but not equally likely
d)
mutually exclusive and independent
|
|
Hrishikesh Gupta answered |
 and
and 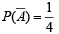
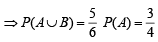
Also ⇒ P(A ∪ B) = P(A) + P(B) - P(A∩ B)
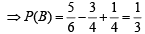
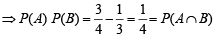
Hence A and B are independent but not equally likely.
Chapter doubts & questions for Probability - 35 Years Chapter wise Previous Year Solved Papers for JEE 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Probability - 35 Years Chapter wise Previous Year Solved Papers for JEE in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily


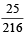
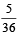
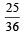
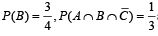 and
and 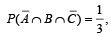 then P (B∩C) is (2003S)
then P (B∩C) is (2003S)
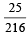
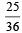
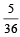
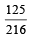
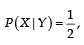
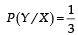 and
and 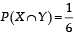 Which of the following is (are) correct ? (2012)
Which of the following is (are) correct ? (2012)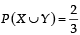
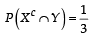
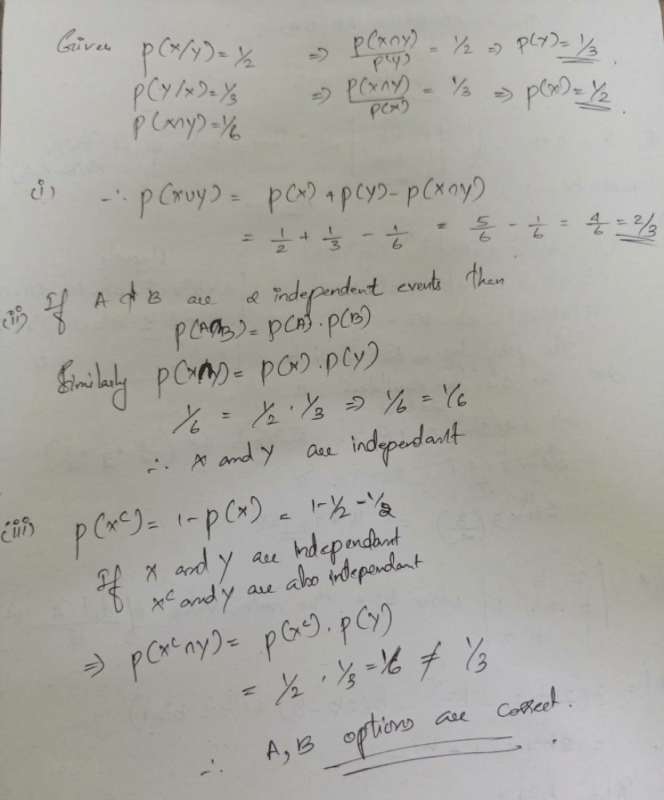
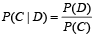

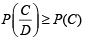
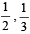 and
and 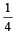 . Probability that the problem is solved is [2002]
. Probability that the problem is solved is [2002]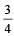

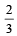
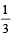
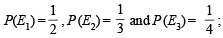
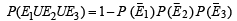
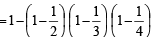
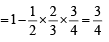
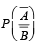 is equal to (Here
is equal to (Here 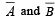 are complements of A and B respectively). (1982 - 2 Marks)
are complements of A and B respectively). (1982 - 2 Marks) 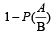
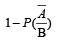
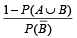
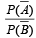
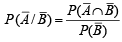
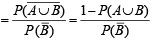

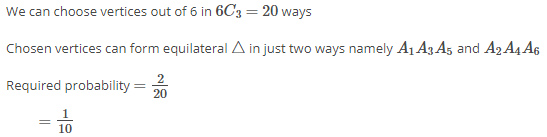
 and
and 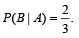 Then P(B) is [2008]
Then P(B) is [2008]