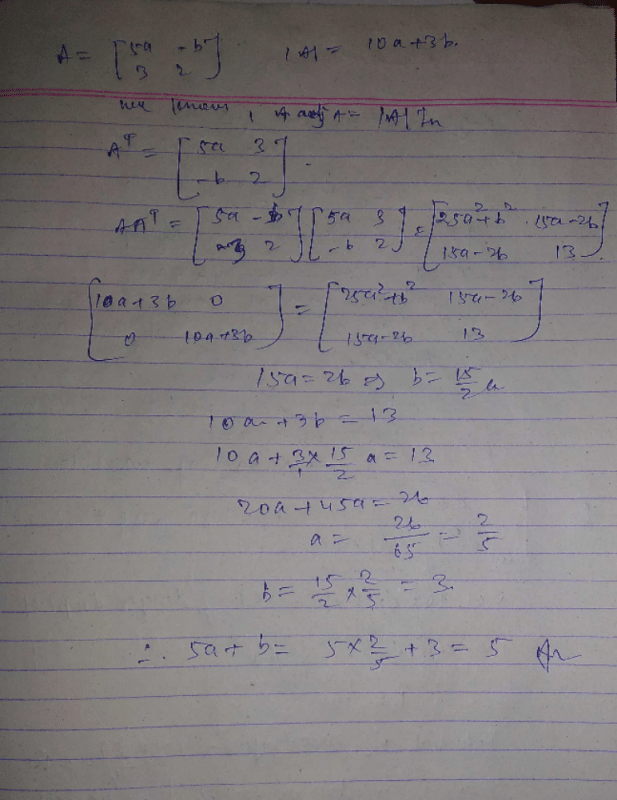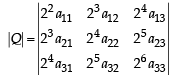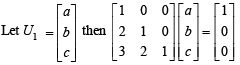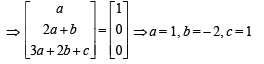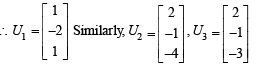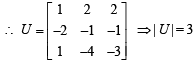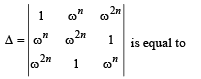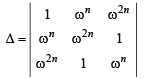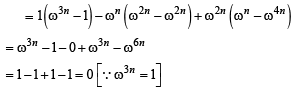All Exams >
JEE >
35 Years Chapter wise Previous Year Solved Papers for JEE >
All Questions
All questions of Matrices and Determinants for JEE Exam
A square matrix in which all the elements except at least the one element in the diagonal are zeros is said to be a- a)identical matrix
- b)null/zero matrix
- c)column matrix
- d)diagonal matrix
Correct answer is option 'D'. Can you explain this answer?
A square matrix in which all the elements except at least the one element in the diagonal are zeros is said to be a
a)
identical matrix
b)
null/zero matrix
c)
column matrix
d)
diagonal matrix
|
|
Krishna Iyer answered |
A diagonal matrix is a matrix in which all of the elements not on the diagonal of a square matrix are 0.
Consider the set A of all determinants of order 3 with entries 0 or 1 only. Let B be the subset of A consisting of all determinants with value 1. Let C be the subset of A consisting of all determinants with value –1. Then
- a)C is empty
- b)B has as many elements as C
- c)A = B∪C
- d)B has twice as many elements as elements as C
Correct answer is option 'B'. Can you explain this answer?
Consider the set A of all determinants of order 3 with entries 0 or 1 only. Let B be the subset of A consisting of all determinants with value 1. Let C be the subset of A consisting of all determinants with value –1. Then
a)
C is empty
b)
B has as many elements as C
c)
A = B∪C
d)
B has twice as many elements as elements as C
|
|
Lekshmi Choudhury answered |

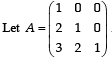 If u1 and u2 are column matrices such that
If u1 and u2 are column matrices such that 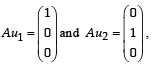 then u1 + u2 is equal to :
then u1 + u2 is equal to :- a)
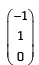
- b)
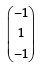
- c)
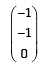
- d)
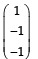
Correct answer is option 'D'. Can you explain this answer?
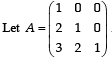 If u1 and u2 are column matrices such that
If u1 and u2 are column matrices such that 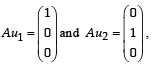 then u1 + u2 is equal to :
then u1 + u2 is equal to :a)
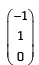
b)
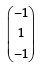
c)
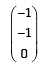
d)
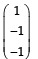
|
|
Chirag Verma answered |
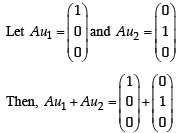
 ..(1)
..(1)
We know,
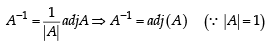
Now, from equation (1), we have
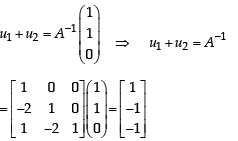
For 3 × 3 matrices M and N, which of the following statement(s) is (are) NOT correct?- a)NTMN is symmetric or skew symmetric, according as M is symmetric or skew symmetric
- b)MN – NM is skew symmetric for all symmetric matrices M and N
- c)MN is symmetric for all symmetric matrices M and N
- d)(adj M) (adj N) = adj (MN) for all invertible matrices M and N
Correct answer is option 'C,D'. Can you explain this answer?
For 3 × 3 matrices M and N, which of the following statement(s) is (are) NOT correct?
a)
NTMN is symmetric or skew symmetric, according as M is symmetric or skew symmetric
b)
MN – NM is skew symmetric for all symmetric matrices M and N
c)
MN is symmetric for all symmetric matrices M and N
d)
(adj M) (adj N) = adj (MN) for all invertible matrices M and N

|
Om Rana answered |

Given 2x – y + 2z = 2, x – 2y + z = – 4, x + y + λz = 4 then the value of λ such that the given system of equation has NO solution, is- a)3
- b)1
- c)0
- d)– 3
Correct answer is option 'B'. Can you explain this answer?
Given 2x – y + 2z = 2, x – 2y + z = – 4, x + y + λz = 4 then the value of λ such that the given system of equation has NO solution, is
a)
3
b)
1
c)
0
d)
– 3
|
|
Harsh Singhal answered |
On taking zero determinant made by their eq.cofficient
we get one value which equal to 1
we get one value which equal to 1
PASSAGE - 1 and U1, U2 and U3 are columns of a 3 × 3 matrix U. If column matrices U1, U2 and U3 satisfying
and U1, U2 and U3 are columns of a 3 × 3 matrix U. If column matrices U1, U2 and U3 satisfying 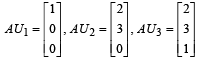 evaluate as directed in the following questionsQ. The sum of the elements of the matrix U–1 is
evaluate as directed in the following questionsQ. The sum of the elements of the matrix U–1 is- a)-1
- b)0
- c)1
- d)3
Correct answer is option 'B'. Can you explain this answer?
PASSAGE - 1
 and U1, U2 and U3 are columns of a 3 × 3 matrix U. If column matrices U1, U2 and U3 satisfying
and U1, U2 and U3 are columns of a 3 × 3 matrix U. If column matrices U1, U2 and U3 satisfying 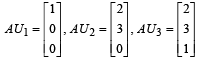 evaluate as directed in the following questions
evaluate as directed in the following questionsQ. The sum of the elements of the matrix U–1 is
a)
-1
b)
0
c)
1
d)
3
|
|
Tejas Verma answered |
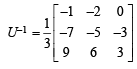
⇒ Sum of elements of
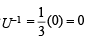
If P is a 3 x 3 matrix such that PT = 2P + I, where PT is the transpose of P and I is the 3 x 3 identity matrix, then there
exists a column matrix 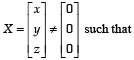
- a)
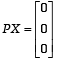
- b)PX = X
- c)PX = 2X
- d)PX = –X
Correct answer is option 'D'. Can you explain this answer?
If P is a 3 x 3 matrix such that PT = 2P + I, where PT is the transpose of P and I is the 3 x 3 identity matrix, then there
exists a column matrix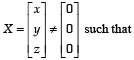
exists a column matrix
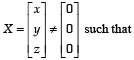
a)
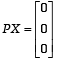
b)
PX = X
c)
PX = 2X
d)
PX = –X
|
|
Rohit Jain answered |
We have PT = 2P + I
⇒ P = 2PT + I ⇒ P = 2(2P + I) + I
⇒ P = 4P + 3I ⇒ P + I = 0
⇒ PX + X = 0 ⇒ PX = – X
⇒ P = 2PT + I ⇒ P = 2(2P + I) + I
⇒ P = 4P + 3I ⇒ P + I = 0
⇒ PX + X = 0 ⇒ PX = – X
Consider the system of linear equations ;x1 + 2x2 + x3 = 3
2x1 + 3x2 + x3 = 3
3x1 + 5x2 + 2x3 = 1The system has- a)exactly 3 solutions
- b)a unique solution
- c)no solution
- d)infinite number of solutions
Correct answer is option 'C'. Can you explain this answer?
Consider the system of linear equations ;
x1 + 2x2 + x3 = 3
2x1 + 3x2 + x3 = 3
3x1 + 5x2 + 2x3 = 1
2x1 + 3x2 + x3 = 3
3x1 + 5x2 + 2x3 = 1
The system has
a)
exactly 3 solutions
b)
a unique solution
c)
no solution
d)
infinite number of solutions

|
Veda Institute answered |
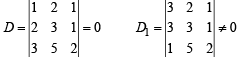
⇒ Given system, does not have any solution.
⇒ No solution
⇒ No solution
The number of values of k for which the system of equations (k + 1)x + 8y = 4k; kx + (k + 3) y = 3k – 1 has infinitely many solutions is- a)0
- b)1
- c)2
- d)infinite
Correct answer is option 'B'. Can you explain this answer?
The number of values of k for which the system of equations (k + 1)x + 8y = 4k; kx + (k + 3) y = 3k – 1 has infinitely many solutions is
a)
0
b)
1
c)
2
d)
infinite
|
|
Shraddha Patel answered |
To solve this system of equations, we can start by multiplying the first equation by k and the second equation by (k - 3):
(k)(k + 1)x + 8ky = 4k^2
kx + (k - 3)y = 3k(k - 3)
Now we can simplify both equations:
k^2x + kx + 8ky = 4k^2
kx + ky - 3y = 3k^2 - 9k
Next, we can subtract the second equation from the first equation:
k^2x - kx + 8ky - ky + 3y = 4k^2 - 3k^2 + 9k - (-9k)
k^2x - kx + 7ky + 4y = k^2 + 18k
Now we can factor out the common terms:
x(k^2 - k) + y(7k + 4) = k(k + 18)
Since the left-hand side is a linear combination of x and y, and the right-hand side is a product of k and (k + 18), we have two cases to consider:
Case 1: k^2 - k = 0
This equation factors as k(k - 1) = 0, which gives us two solutions: k = 0 and k = 1.
Case 2: 7k + 4 = k + 18
This equation simplifies to 6k = 14, which gives us a single solution: k = 7/3.
Therefore, there are three values of k for which the system of equations is satisfied: k = 0, k = 1, and k = 7/3.
(k)(k + 1)x + 8ky = 4k^2
kx + (k - 3)y = 3k(k - 3)
Now we can simplify both equations:
k^2x + kx + 8ky = 4k^2
kx + ky - 3y = 3k^2 - 9k
Next, we can subtract the second equation from the first equation:
k^2x - kx + 8ky - ky + 3y = 4k^2 - 3k^2 + 9k - (-9k)
k^2x - kx + 7ky + 4y = k^2 + 18k
Now we can factor out the common terms:
x(k^2 - k) + y(7k + 4) = k(k + 18)
Since the left-hand side is a linear combination of x and y, and the right-hand side is a product of k and (k + 18), we have two cases to consider:
Case 1: k^2 - k = 0
This equation factors as k(k - 1) = 0, which gives us two solutions: k = 0 and k = 1.
Case 2: 7k + 4 = k + 18
This equation simplifies to 6k = 14, which gives us a single solution: k = 7/3.
Therefore, there are three values of k for which the system of equations is satisfied: k = 0, k = 1, and k = 7/3.
PASSAGE - 2Let  be the set of all 3× 3 symmetric matrices all of whose entries are either 0 or 1. Five of these entries are 1 and four of them are 0.Q. The number of matrices A in
be the set of all 3× 3 symmetric matrices all of whose entries are either 0 or 1. Five of these entries are 1 and four of them are 0.Q. The number of matrices A in 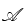 for which the system of linear equations
for which the system of linear equations 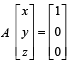
- a)0
- b)more than 2
- c)2
- d)1
Correct answer is option 'B'. Can you explain this answer?
PASSAGE - 2
Let 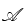 be the set of all 3× 3 symmetric matrices all of whose entries are either 0 or 1. Five of these entries are 1 and four of them are 0.
be the set of all 3× 3 symmetric matrices all of whose entries are either 0 or 1. Five of these entries are 1 and four of them are 0.
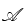 be the set of all 3× 3 symmetric matrices all of whose entries are either 0 or 1. Five of these entries are 1 and four of them are 0.
be the set of all 3× 3 symmetric matrices all of whose entries are either 0 or 1. Five of these entries are 1 and four of them are 0.Q. The number of matrices A in  for which the system of linear equations
for which the system of linear equations
 for which the system of linear equations
for which the system of linear equations 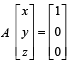
a)
0
b)
more than 2
c)
2
d)
1
|
|
Aman Chauhan answered |
For the given system to be inconsistent |A| = 0. The matrices for which | A | = 0 are
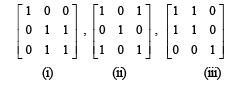
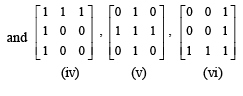
We find for A = (i)
By Cramer’s rule D1 = 0 = D2=D3
∴ infinite many solution
For A = (ii)
By Cramer ’s rule D1 ≠ 0
⇒ no solution i.e. inconsistent.
Similarly we find the system as inconsistent in cases (iii), (v) and (vi).
Hence for four cases system is inconsistent.
The system of equationsα x + y + z = α – 1
x + α y + z = α – 1
x + y + α z = α – 1has infinite solutions, if α is- a)– 2
- b)either – 2 or 1
- c)not – 2
- d)1
Correct answer is option 'A'. Can you explain this answer?
The system of equations
α x + y + z = α – 1
x + α y + z = α – 1
x + y + α z = α – 1
x + α y + z = α – 1
x + y + α z = α – 1
has infinite solutions, if α is
a)
– 2
b)
either – 2 or 1
c)
not – 2
d)
1
|
|
Madhurima Mehta answered |
α x + y + z = α -1
x + α y + z = α – 1;
x + y + z α = α – 1
x + α y + z = α – 1;
x + y + z α = α – 1
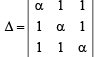
= α(α2 - 1) - 1(α - 1) + 1(1 - α)
= α (α-1)(α+1) - 1(α-1) - 1(α-1)
For infinite solutions, Δ = 0
⇒ (α - 1)[α2 + α - 1 - 1] = 0
= α (α-1)(α+1) - 1(α-1) - 1(α-1)
For infinite solutions, Δ = 0
⇒ (α - 1)[α2 + α - 1 - 1] = 0
⇒ (α - 1)[α2 + α - 2] = 0 ⇒ α = – 2,1;
But a ≠ 1 . ∴ α = – 2
Let P and Q be 3 x 3 matrices P ≠ Q. If P3 = Q3 and P2Q = Q2P then determinant of (P2 + Q2) is equal to :- a)–2
- b)1
- c)0
- d)–1
Correct answer is option 'C'. Can you explain this answer?
Let P and Q be 3 x 3 matrices P ≠ Q. If P3 = Q3 and P2Q = Q2P then determinant of (P2 + Q2) is equal to :
a)
–2
b)
1
c)
0
d)
–1
|
|
Harshitha Saha answered |
Given P3 = Q3 ...(1)
and P2Q = Q2P ...(2)
Subtracting (1) and (2), we get
P3 – P2Q = Q3 – Q2P
⇒ P2 (P–Q) + Q2 (P – Q) = 0
⇒ (P2 + Q2) (P–Q) = 0 ⇒ |P2 + Q2| = 0 as P ≠ Q
and P2Q = Q2P ...(2)
Subtracting (1) and (2), we get
P3 – P2Q = Q3 – Q2P
⇒ P2 (P–Q) + Q2 (P – Q) = 0
⇒ (P2 + Q2) (P–Q) = 0 ⇒ |P2 + Q2| = 0 as P ≠ Q
Let X and Y be two arbitrary, 3 × 3, non-zero, skew-symmetric matrices and Z be an arbitrary 3 × 3, non zero, symmetric matrix. Then which of the following matrices is (are) skew symmetric?- a)Y3Z4 – Z4Y3
- b)X44 + Y44
- c)X4Z3 – Z3X4
- d)X23 + Y23
Correct answer is option 'C,D'. Can you explain this answer?
Let X and Y be two arbitrary, 3 × 3, non-zero, skew-symmetric matrices and Z be an arbitrary 3 × 3, non zero, symmetric matrix. Then which of the following matrices is (are) skew symmetric?
a)
Y3Z4 – Z4Y3
b)
X44 + Y44
c)
X4Z3 – Z3X4
d)
X23 + Y23
|
|
Devika Choudhury answered |
X ' = –X, Y ' = –Y, Z ' = Z
(Y3Z4 – Z4Y3)' = (Z4)'(Y3)' – (Y3)'(Z4)'
= (Z')4(Y')3 – (Y')3(Z')4
= –Z4Y3 + Y3Z4 = Y3Z4 – Z4Y3
(Y3Z4 – Z4Y3)' = (Z4)'(Y3)' – (Y3)'(Z4)'
= (Z')4(Y')3 – (Y')3(Z')4
= –Z4Y3 + Y3Z4 = Y3Z4 – Z4Y3
∴ Symmetric matrix.
Similarly X44 + Y44 is symmetric matrix and X4Z3 – Z3X4 and X23 + Y23 are skew symmetric matrices.
Similarly X44 + Y44 is symmetric matrix and X4Z3 – Z3X4 and X23 + Y23 are skew symmetric matrices.
Let ω be a complex cube root of unity with ω ≠ 1 and P = [pij] be a n × n matrix with pij = ωi+j. Then p2 ≠ 0, when n =- a)57
- b)55
- c)58
- d)56
Correct answer is option 'B,C,D'. Can you explain this answer?
Let ω be a complex cube root of unity with ω ≠ 1 and P = [pij] be a n × n matrix with pij = ωi+j. Then p2 ≠ 0, when n =
a)
57
b)
55
c)
58
d)
56
|
|
Sharmila Choudhury answered |
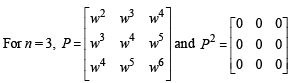
It shows P2 = 0 if n is a multiple of 3.
So for P2 ≠ 0, n should not be a multiple of 3 i.e. n can take values 55, 58, 56
So for P2 ≠ 0, n should not be a multiple of 3 i.e. n can take values 55, 58, 56
Let M and N be two 3 × 3 matrices such that MN = NM. Further, if M ≠ N2 and M2 = N4, then- a)determinant of (M2 + MN2) is 0
- b)there is 3 × 3 non-zero matrix U such that (M2 + MN2)U is the zero matrix
- c)determinant of (M2 + MN2) > 1
- d)for a 3 × 3 matrix U, if (M2 + MN2)U equals the zero matrix then U is the zero matrix
Correct answer is option 'A,B'. Can you explain this answer?
Let M and N be two 3 × 3 matrices such that MN = NM. Further, if M ≠ N2 and M2 = N4, then
a)
determinant of (M2 + MN2) is 0
b)
there is 3 × 3 non-zero matrix U such that (M2 + MN2)U is the zero matrix
c)
determinant of (M2 + MN2) > 1
d)
for a 3 × 3 matrix U, if (M2 + MN2)U equals the zero matrix then U is the zero matrix
|
|
Kajal Dey answered |
Given MN = NM, M ≠ N2 and M2 = N4.
Then M2 = N4 ⇒ (M + N2) (M – N 2) = 0
⇒ (i) M + N2 = 0 and M – N2 ≠ 0
(ii) |M + N2| = 0 and |M – N2| = 0
In each case |M + N2| = 0
∴ |M2 + MN2| = |M| |M + N2| = 0
∴ (a) is correct and (c) is not correct.
Also we know if |A| = 0, then there can be many matrices U, such that AU = 0
∴ (M2 + MN2)U = 0 will be true for many values of U.
Hence (b) is correct.
Again if AX = 0 and |A| = 0, then X can be non-zero.
∴ (d) is not correct.
Then M2 = N4 ⇒ (M + N2) (M – N 2) = 0
⇒ (i) M + N2 = 0 and M – N2 ≠ 0
(ii) |M + N2| = 0 and |M – N2| = 0
In each case |M + N2| = 0
∴ |M2 + MN2| = |M| |M + N2| = 0
∴ (a) is correct and (c) is not correct.
Also we know if |A| = 0, then there can be many matrices U, such that AU = 0
∴ (M2 + MN2)U = 0 will be true for many values of U.
Hence (b) is correct.
Again if AX = 0 and |A| = 0, then X can be non-zero.
∴ (d) is not correct.
Let A and B be two symmetric matrices of order 3.Statement-1: A(BA) and (AB)A are symmetric matrices.
Statement-2: AB is symmetric matrix if matrix multiplication of A with B is commutative.- a)Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1.
- b)Statement-1 is true, Statement-2 is false.
- c)Statement-1 is false, Statement-2 is true.
- d)Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1.
Correct answer is option 'A'. Can you explain this answer?
Let A and B be two symmetric matrices of order 3.
Statement-1: A(BA) and (AB)A are symmetric matrices.
Statement-2: AB is symmetric matrix if matrix multiplication of A with B is commutative.
Statement-2: AB is symmetric matrix if matrix multiplication of A with B is commutative.
a)
Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1.
b)
Statement-1 is true, Statement-2 is false.
c)
Statement-1 is false, Statement-2 is true.
d)
Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1.
|
|
Ishan Chatterjee answered |
Explanation:
Statement-1: A(BA) and (AB)A are symmetric matrices.
Let C = AB. Then, (AB)A = CAB and A(BA) = CBA. Now, we have to prove that C^T = C.
Since A and B are symmetric matrices, we have:
A^T = A and B^T = B
Now, we can write:
C^T = (AB)^T = B^T A^T = BA = C
Therefore, C^T = C, which implies that (AB)A and A(BA) are symmetric matrices.
Statement-2: AB is a symmetric matrix if matrix multiplication of A with B is commutative.
If AB is a symmetric matrix then AB = (AB)^T = B^T A^T = BA. Hence, the matrix multiplication of A with B is commutative. However, the converse is not true. That is, just because A and B commute, it does not necessarily imply that AB is symmetric.
Option A: Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1.
From the above explanation, we can see that both statements are true. However, Statement-2 does not explain why Statement-1 is true. Therefore, option A is the correct answer.
Statement-1: A(BA) and (AB)A are symmetric matrices.
Let C = AB. Then, (AB)A = CAB and A(BA) = CBA. Now, we have to prove that C^T = C.
Since A and B are symmetric matrices, we have:
A^T = A and B^T = B
Now, we can write:
C^T = (AB)^T = B^T A^T = BA = C
Therefore, C^T = C, which implies that (AB)A and A(BA) are symmetric matrices.
Statement-2: AB is a symmetric matrix if matrix multiplication of A with B is commutative.
If AB is a symmetric matrix then AB = (AB)^T = B^T A^T = BA. Hence, the matrix multiplication of A with B is commutative. However, the converse is not true. That is, just because A and B commute, it does not necessarily imply that AB is symmetric.
Option A: Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1.
From the above explanation, we can see that both statements are true. However, Statement-2 does not explain why Statement-1 is true. Therefore, option A is the correct answer.
Let M be a 2 × 2 symmetric matrix with integer entries. Then M is invertible if- a)The first column of M is the transpose of the second row of M
- b)The second row of M is the transpose of the first column of M
- c)M is a diagonal matrix with non-zero entries in the main diagonal
- d)The product of entries in the main diagonal of M is not the square of an integer
Correct answer is option 'C,D'. Can you explain this answer?
Let M be a 2 × 2 symmetric matrix with integer entries. Then M is invertible if
a)
The first column of M is the transpose of the second row of M
b)
The second row of M is the transpose of the first column of M
c)
M is a diagonal matrix with non-zero entries in the main diagonal
d)
The product of entries in the main diagonal of M is not the square of an integer
|
|
Upasana Singh answered |
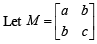 where a, b, c are integers.
where a, b, c are integers.M is invertible if 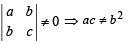
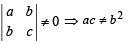
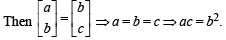
∴ (a) is not correct.
If [bc] = [ab] ⇒ b = a = c ⇒ ac = b2
∴ (b) is not correct.

∴ M is invertible.
(c) is correct
As ac ≠ (integer)2 ⇒ ac ≠ b2
∴ (d) is correct.
(c) is correct
As ac ≠ (integer)2 ⇒ ac ≠ b2
∴ (d) is correct.
If A and B are square matrices of equal degree, then which one is correct among the followings?- a)A + B = B + A
- b)A + B = A – B
- c)A – B = B – A
- d)AB = BA
Correct answer is option 'A'. Can you explain this answer?
If A and B are square matrices of equal degree, then which one is correct among the followings?
a)
A + B = B + A
b)
A + B = A – B
c)
A – B = B – A
d)
AB = BA
|
|
Lavanya Menon answered |
If A and B are square matrices of same degree then matrices A and B can be added or subtracted or multiplied. By algebra of matrices the only correct option is A + B = B + A
The number of 3 × 3 non-singular matrices, with four entries as 1 and all other entries as 0, is- a)5
- b)6
- c)at least 7
- d)less than 4
Correct answer is option 'C'. Can you explain this answer?
The number of 3 × 3 non-singular matrices, with four entries as 1 and all other entries as 0, is
a)
5
b)
6
c)
at least 7
d)
less than 4
|
|
Siddharth Roy answered |
 are 6 non-singular matrices because 6 blanks will be filled by 5 zeros and 1 one.
are 6 non-singular matrices because 6 blanks will be filled by 5 zeros and 1 one. Similarly,
 are 6 non-singular matrices.
are 6 non-singular matrices.So, required cases are more than 7, non-singular 3 × 3 matrices.
If the system of equations x + ay = 0, az + y = 0 and ax + z = 0 has infinite solutions, then the value of a is- a)–1
- b)1
- c)0
- d)no real values
Correct answer is option 'A'. Can you explain this answer?
If the system of equations x + ay = 0, az + y = 0 and ax + z = 0 has infinite solutions, then the value of a is
a)
–1
b)
1
c)
0
d)
no real values
|
|
Hridoy Shah answered |
We can see that the system of equations has infinite solutions if and only if at least one of the variables x, y, z is equal to 0.
If x = 0, then the first equation becomes 0 = 0, which is always true. The second equation becomes az = 0, which means that either a = 0 or z = 0. The third equation becomes 0 = 0, which is always true. If a = 0, then the second equation becomes 0y = 0, which is always true. If z = 0, then the third equation becomes 0 = 0, which is always true. Therefore, if x = 0, then the system has infinite solutions for any value of a.
If y = 0, then the first equation becomes ax = 0, which means that either a = 0 or x = 0. The second equation becomes 0 = 0, which is always true. The third equation becomes az = 0, which means that either a = 0 or z = 0. If a = 0, then the first equation becomes 0 = 0, which is always true. If x = 0 and z = 0, then the system has infinite solutions for any value of a. If x = 0 and z ≠ 0, or x ≠ 0 and z = 0, then the system has no solutions. Therefore, if y = 0, then the system has infinite solutions if and only if either a = 0 or x = 0 and z = 0.
If z = 0, then the first equation becomes ax = 0, which means that either a = 0 or x = 0. The second equation becomes 0y = 0, which is always true. The third equation becomes ax = 0, which means that either a = 0 or x = 0. If a = 0, then the first and third equations become 0 = 0, which is always true. If x = 0 and y = 0, then the system has infinite solutions for any value of a. If x = 0 and y ≠ 0, or x ≠ 0 and y = 0, then the system has no solutions. Therefore, if z = 0, then the system has infinite solutions if and only if either a = 0 or x = 0 and y = 0.
From the above analysis, we can see that the system has infinite solutions if and only if at least one of the variables x, y, z is equal to 0, and either a = 0 or x = 0 and y = 0 or x = 0 and z = 0. Therefore, the value of a can be any real number except 0.
If x = 0, then the first equation becomes 0 = 0, which is always true. The second equation becomes az = 0, which means that either a = 0 or z = 0. The third equation becomes 0 = 0, which is always true. If a = 0, then the second equation becomes 0y = 0, which is always true. If z = 0, then the third equation becomes 0 = 0, which is always true. Therefore, if x = 0, then the system has infinite solutions for any value of a.
If y = 0, then the first equation becomes ax = 0, which means that either a = 0 or x = 0. The second equation becomes 0 = 0, which is always true. The third equation becomes az = 0, which means that either a = 0 or z = 0. If a = 0, then the first equation becomes 0 = 0, which is always true. If x = 0 and z = 0, then the system has infinite solutions for any value of a. If x = 0 and z ≠ 0, or x ≠ 0 and z = 0, then the system has no solutions. Therefore, if y = 0, then the system has infinite solutions if and only if either a = 0 or x = 0 and z = 0.
If z = 0, then the first equation becomes ax = 0, which means that either a = 0 or x = 0. The second equation becomes 0y = 0, which is always true. The third equation becomes ax = 0, which means that either a = 0 or x = 0. If a = 0, then the first and third equations become 0 = 0, which is always true. If x = 0 and y = 0, then the system has infinite solutions for any value of a. If x = 0 and y ≠ 0, or x ≠ 0 and y = 0, then the system has no solutions. Therefore, if z = 0, then the system has infinite solutions if and only if either a = 0 or x = 0 and y = 0.
From the above analysis, we can see that the system has infinite solutions if and only if at least one of the variables x, y, z is equal to 0, and either a = 0 or x = 0 and y = 0 or x = 0 and z = 0. Therefore, the value of a can be any real number except 0.
Let A be a square matrix all of whose entries are integers. Then which one of the following is true?- a)If det A = ± 1, then A–1 exists but all its entries are not necessarily integers
- b)If det A ≠ ± 1, then A–1 exists and all its entries are non integers
- c)If det A = ± 1, then A–1 exists but all its entries are integers
- d)If det A = ± 1, then A–1 need not exists
Correct answer is option 'C'. Can you explain this answer?
Let A be a square matrix all of whose entries are integers. Then which one of the following is true?
a)
If det A = ± 1, then A–1 exists but all its entries are not necessarily integers
b)
If det A ≠ ± 1, then A–1 exists and all its entries are non integers
c)
If det A = ± 1, then A–1 exists but all its entries are integers
d)
If det A = ± 1, then A–1 need not exists
|
|
Maitri Das answered |
Explanation:
Given:
- A is a square matrix with all integer entries
- det(A) = ±1
Explanation:
If det A = ±1:
- If the determinant of matrix A is ±1, then A is invertible.
- This means that A has an inverse denoted by A^-1.
- Since A is a square matrix with all integer entries, the inverse A^-1 also exists.
- Therefore, if det A = ±1, then A^-1 exists.
But all its entries are not necessarily integers:
- While A^-1 exists when det A = ±1, it does not necessarily mean that all the entries of A^-1 will be integers.
- The entries of A^-1 can be fractions or decimals, even if the entries of A are integers.
Conclusion:
- Option (c) is true: If det A = ±1, then A^-1 exists but all its entries are not necessarily integers.
Given:
- A is a square matrix with all integer entries
- det(A) = ±1
Explanation:
If det A = ±1:
- If the determinant of matrix A is ±1, then A is invertible.
- This means that A has an inverse denoted by A^-1.
- Since A is a square matrix with all integer entries, the inverse A^-1 also exists.
- Therefore, if det A = ±1, then A^-1 exists.
But all its entries are not necessarily integers:
- While A^-1 exists when det A = ±1, it does not necessarily mean that all the entries of A^-1 will be integers.
- The entries of A^-1 can be fractions or decimals, even if the entries of A are integers.
Conclusion:
- Option (c) is true: If det A = ±1, then A^-1 exists but all its entries are not necessarily integers.
Let A be a 2 × 2 matrix with real entries. Let I be the 2 × 2 identity matrix. Denote by tr(A), the sum of diagonal entries of a. Assume that A2 = I.Statement-1 : If A ≠ I and A ≠ –I, then det(A) = –1Statement-2 : If A ≠ I and A ≠ –I, then tr (A) ≠ 0.- a)Statement -1 is false, Statement-2 is true
- b)Statement -1 is true, Statement-2 is true; Statement -2 is a correct explanation for Statement-1
- c)Statement -1 is true, Statement-2 is true; Statement -2 is not a correct explanation for Statement-1
- d)Statement -1 is true, Statement-2 is false
Correct answer is option 'D'. Can you explain this answer?
Let A be a 2 × 2 matrix with real entries. Let I be the 2 × 2 identity matrix. Denote by tr(A), the sum of diagonal entries of a. Assume that A2 = I.
Statement-1 : If A ≠ I and A ≠ –I, then det(A) = –1
Statement-2 : If A ≠ I and A ≠ –I, then tr (A) ≠ 0.
a)
Statement -1 is false, Statement-2 is true
b)
Statement -1 is true, Statement-2 is true; Statement -2 is a correct explanation for Statement-1
c)
Statement -1 is true, Statement-2 is true; Statement -2 is not a correct explanation for Statement-1
d)
Statement -1 is true, Statement-2 is false
|
|
Anand Kumar answered |
Let, A11=a, A12=a, A21=a, A22=-a form the required matrix using these entries and then check the condition given you will see Option D is correct.
If A and B are square matrices of size n × n such that A2 - B2 = (A -B)(A+B), then which of the following will be always true?- a)A = B
- b)AB = BA
- c)either of A or B is a zero matrix
- d)either of A or B is identity matrix
Correct answer is option 'B'. Can you explain this answer?
If A and B are square matrices of size n × n such that A2 - B2 = (A -B)(A+B), then which of the following will be always true?
a)
A = B
b)
AB = BA
c)
either of A or B is a zero matrix
d)
either of A or B is identity matrix
|
|
Ruchi Tiwari answered |
A2 - B2 = (A -B)(A+B)
A2 - B2 = A2 + AB - BA-B2 ⇒ AB = BA
A2 - B2 = A2 + AB - BA-B2 ⇒ AB = BA
If A is a 3 × 3 non-singular matrix such that AA' = A'A and B = A–1A', then BB' equals:- a)B –1
- b)(B -1)'
- c)I +B
- d)I
Correct answer is option 'D'. Can you explain this answer?
If A is a 3 × 3 non-singular matrix such that AA' = A'A and B = A–1A', then BB' equals:
a)
B –1
b)
(B -1)'
c)
I +B
d)
I
|
|
Sparsh Majumdar answered |
BB' = B(A-1 A')' = B(A ')'(A-1)' = BA (A–1)'
= (A -1 A')(A(A-1)')
= A–1A .A'.(A–1)' {as AA' = A'A}
= I(A–1A)'
= I.I = I2 = I
= (A -1 A')(A(A-1)')
= A–1A .A'.(A–1)' {as AA' = A'A}
= I(A–1A)'
= I.I = I2 = I
Let a, b, c be any real numbers. Suppose that there are real numbers x, y, z not all zero such that x = cy + bz, y = az + cx, and z = bx + ay. Then a2 + b2 + c2 + 2abc is equal to- a)2
- b)–1
- c)0
- d)1
Correct answer is option 'D'. Can you explain this answer?
Let a, b, c be any real numbers. Suppose that there are real numbers x, y, z not all zero such that x = cy + bz, y = az + cx, and z = bx + ay. Then a2 + b2 + c2 + 2abc is equal to
a)
2
b)
–1
c)
0
d)
1
|
|
Abhishek Majumdar answered |
The given equations are
–x + cy + bz = 0
cx –y + az = 0
bx + ay – z = 0
∵ x, y, z are not all zero
–x + cy + bz = 0
cx –y + az = 0
bx + ay – z = 0
∵ x, y, z are not all zero
∴ The above system should not have unique (zero) solution
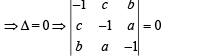
⇒ –1(1– a2) – c(– c – ab) + b(ac + b) = 0
⇒–1 + a2 + b2 + c2 + 2abc = 0
⇒ a2 + b2 + c2 + 2abc = 1
⇒–1 + a2 + b2 + c2 + 2abc = 0
⇒ a2 + b2 + c2 + 2abc = 1
If the system of linear equations x + 2ay +az = 0 ; x +3by+bz = 0 ; x +4cy+cz = 0 ; has a non - zero solution, then a, b, c.- a) satisfy a + 2b + 3c = 0
- b)are in A.P
- c) are in G..P
- d)are in H.P.
Correct answer is option 'D'. Can you explain this answer?
If the system of linear equations
x + 2ay +az = 0 ; x +3by+bz = 0 ; x +4cy+cz = 0 ; has a non - zero solution, then a, b, c.
a)
satisfy a + 2b + 3c = 0
b)
are in A.P
c)
are in G..P
d)
are in H.P.
|
|
Nidhi Singh answered |
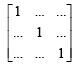
For homogeneous system of equations to have non zero solution, Δ = 0
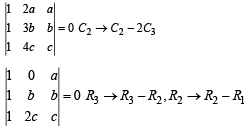
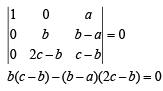
On simplification, 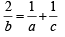
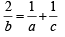
∴ a,b,c are in Harmonic Progression.
If ω (≠1) is a cube root of unity, then
- a)0
- b)1
- c)i
- d)ω
Correct answer is option 'A'. Can you explain this answer?
If ω (≠1) is a cube root of unity, then

a)
0
b)
1
c)
i
d)
ω

|
Roshni Chavan answered |
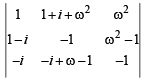
Operating R1→ R1 – R2 + R3
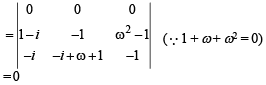
If the adjoint of a 3 x 3 matrix P is  then the possible value(s) of the determinant of P is (are)
then the possible value(s) of the determinant of P is (are) - a)–2
- b)–1
- c)1
- d)2
Correct answer is option 'A,D'. Can you explain this answer?
If the adjoint of a 3 x 3 matrix P is  then the possible value(s) of the determinant of P is (are)
then the possible value(s) of the determinant of P is (are)
 then the possible value(s) of the determinant of P is (are)
then the possible value(s) of the determinant of P is (are) a)
–2
b)
–1
c)
1
d)
2
|
|
Mahi Sarkar answered |
ANSWER :- a,d
Solution :- |adj P| = |P|^2 as (adj(P)| = |P|^(n-1))
|adj P| = 1(3-7) -4(6-7) +4(2-1) = 4
Hence, |P| = 2 or -2
PASSAGE - 2Let  be the set of all 3× 3 symmetric matrices all of whose entries are either 0 or 1. Five of these entries are 1 and four of them are 0.Q. The number of matrices in
be the set of all 3× 3 symmetric matrices all of whose entries are either 0 or 1. Five of these entries are 1 and four of them are 0.Q. The number of matrices in  is
is- a)12
- b)6
- c)9
- d)3
Correct answer is option 'A'. Can you explain this answer?
PASSAGE - 2
Let  be the set of all 3× 3 symmetric matrices all of whose entries are either 0 or 1. Five of these entries are 1 and four of them are 0.
be the set of all 3× 3 symmetric matrices all of whose entries are either 0 or 1. Five of these entries are 1 and four of them are 0.
 be the set of all 3× 3 symmetric matrices all of whose entries are either 0 or 1. Five of these entries are 1 and four of them are 0.
be the set of all 3× 3 symmetric matrices all of whose entries are either 0 or 1. Five of these entries are 1 and four of them are 0.Q. The number of matrices in  is
is
 is
isa)
12
b)
6
c)
9
d)
3
|
|
Soumya Nambiar answered |
Each element of set A is 3 × 3 symmetric matrix with five of its entries as 1 and four of its entries as 0, we can keep in diagonal either 2 zero and one 1 or no zero and three 1 so that the left over zeros and one’s are even in number.
Hence taking 2 zeros and one 1 in diagonal the possible cases are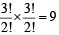
and taking 3 ones in diagonal the possible cases are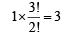
∴ Total elements A can have = 9 + 3 = 12
Hence taking 2 zeros and one 1 in diagonal the possible cases are
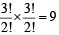
and taking 3 ones in diagonal the possible cases are
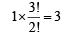
∴ Total elements A can have = 9 + 3 = 12
The number of 3 × 3 matrices A whose entries are either 0 or1 and for which the system 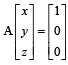 has exactly twodistinct solutions, is
has exactly twodistinct solutions, is- a)0
- b)29–1
- c)168
- d)2
Correct answer is option 'A'. Can you explain this answer?
The number of 3 × 3 matrices A whose entries are either 0 or1 and for which the system 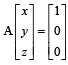 has exactly twodistinct solutions, is
has exactly twodistinct solutions, is
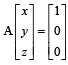 has exactly twodistinct solutions, is
has exactly twodistinct solutions, isa)
0
b)
29–1
c)
168
d)
2
|
|
Arpita Shah answered |
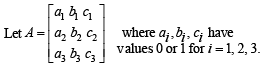
Then the given system is equivalent to
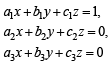
Which represents three distinct planes. But three planes can not intersect at two distinct points, therefore no such system exists.
If a2 + b2 + c2 = – 2 and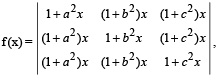 then f (x) is a polynomial of degree
then f (x) is a polynomial of degree- a)1
- b)0
- c)3
- d)2
Correct answer is option 'D'. Can you explain this answer?
If a2 + b2 + c2 = – 2 and
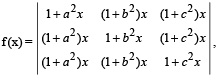
then f (x) is a polynomial of degree
a)
1
b)
0
c)
3
d)
2
|
|
Srestha Basak answered |
Applying, C1 → C1 + C2 + C3 we get
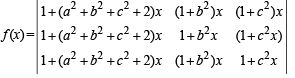

[As given that a2 + b2 + c2 = –2]
∴ a2 +b2+c2 + 2 = 0
Applying R1 → R1-R2 , R2 → R2-R3
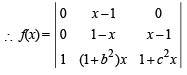
f (x) = ( x - 1)2 Hence degree = 2.
Let 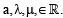 Consider th e system of lin ear equationsax + 2y = λ
Consider th e system of lin ear equationsax + 2y = λ
3x – 2y = μWhich of the following statement(s) is (are) correct?- a)If a = –3, then the system has infinitely many solutions for all values of λ and μ .
- b)If a ≠ –3, then the system has a unique solution for all values of λ and μ .
- c)If λ + μ = 0, then the system has infinitely man y solutions for a = –3.
- d)If λ + μ ≠ 0, then the system has no solution for a = –3.
Correct answer is option 'B,C,D'. Can you explain this answer?
Let 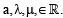 Consider th e system of lin ear equations
Consider th e system of lin ear equations
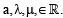 Consider th e system of lin ear equations
Consider th e system of lin ear equationsax + 2y = λ
3x – 2y = μ
3x – 2y = μ
Which of the following statement(s) is (are) correct?
a)
If a = –3, then the system has infinitely many solutions for all values of λ and μ .
b)
If a ≠ –3, then the system has a unique solution for all values of λ and μ .
c)
If λ + μ = 0, then the system has infinitely man y solutions for a = –3.
d)
If λ + μ ≠ 0, then the system has no solution for a = –3.
|
|
Prisha Das answered |
ax + 2y = λ
3x – 2y = μ
3x – 2y = μ
For unique solution, 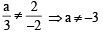
∴ (b) is the correct option.
For infinite many solutions and a = – 3
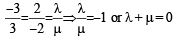
∴ (c) is the correct option.
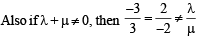
⇒ system has no solution.
⇒ (d) is the correct option.
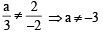
∴ (b) is the correct option.
For infinite many solutions and a = – 3
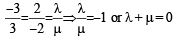
∴ (c) is the correct option.
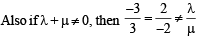
⇒ system has no solution.
⇒ (d) is the correct option.
Let 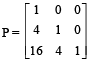 and I be the identity matrix of order 3. If Q = [qij] is a m atrix such that P50 – Q = I, then
and I be the identity matrix of order 3. If Q = [qij] is a m atrix such that P50 – Q = I, then 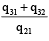 equals
equals- a)52
- b)103
- c)201
- d)205
Correct answer is option 'B'. Can you explain this answer?
Let 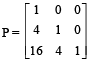 and I be the identity matrix of order 3. If Q = [qij] is a m atrix such that P50 – Q = I, then
and I be the identity matrix of order 3. If Q = [qij] is a m atrix such that P50 – Q = I, then 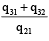 equals
equals
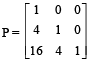 and I be the identity matrix of order 3. If Q = [qij] is a m atrix such that P50 – Q = I, then
and I be the identity matrix of order 3. If Q = [qij] is a m atrix such that P50 – Q = I, then 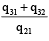 equals
equalsa)
52
b)
103
c)
201
d)
205
|
|
Preethi Nambiar answered |
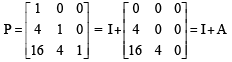
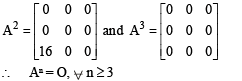
Now P50 = (I + A)50 = 50C0 I50 + 50C1 I49 A + 50C2 I48 A2 + O
= I + 50A + 25 × 49 A2.
∴ Q = P50 – I = 50A + 25 × 49 A2.
⇒ q21 = 50 × 4 = 200
⇒ q31 = 50 × 16 + 25 × 49 × 16 = 20400
⇒ q32 = 50 × 4 = 200
= I + 50A + 25 × 49 A2.
∴ Q = P50 – I = 50A + 25 × 49 A2.
⇒ q21 = 50 × 4 = 200
⇒ q31 = 50 × 16 + 25 × 49 × 16 = 20400
⇒ q32 = 50 × 4 = 200
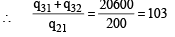
Consider the system of equationsx – 2y + 3z = –1
–x + y – 2z = k
x – 3y + 4z = 1STATEMENT - 1 : The system of equations has no solution for k ¹ 3 andSTATEMENT-2 : The determinant 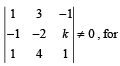 k ≠ 3 .
k ≠ 3 .- a)STATEMENT - 1 is True, STATEMENT - 2 is True; STATEMENT - 2 is a correct explanation for STATEMENT - 1
- b)STATEMENT - 1 is True, STATEMENT - 2 is True; STATEMENT - 2 is NOT a correct explaination for STATEMENT - 1
- c)STATEMENT - 1 is True, STATEMENT - 2 is False
- d)STATEMENT - 1 is False, STATEMENT - 2 is True
Correct answer is option 'A'. Can you explain this answer?
Consider the system of equations
x – 2y + 3z = –1
–x + y – 2z = k
x – 3y + 4z = 1
–x + y – 2z = k
x – 3y + 4z = 1
STATEMENT - 1 : The system of equations has no solution for k ¹ 3 and
STATEMENT-2 : The determinant 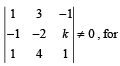 k ≠ 3 .
k ≠ 3 .
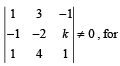 k ≠ 3 .
k ≠ 3 .a)
STATEMENT - 1 is True, STATEMENT - 2 is True; STATEMENT - 2 is a correct explanation for STATEMENT - 1
b)
STATEMENT - 1 is True, STATEMENT - 2 is True; STATEMENT - 2 is NOT a correct explaination for STATEMENT - 1
c)
STATEMENT - 1 is True, STATEMENT - 2 is False
d)
STATEMENT - 1 is False, STATEMENT - 2 is True
|
|
Niharika Gupta answered |
The given equations are
x – 2y + 3z = – 1
– x + y – 2z = k
x – 3y + 4z =1
x – 2y + 3z = – 1
– x + y – 2z = k
x – 3y + 4z =1
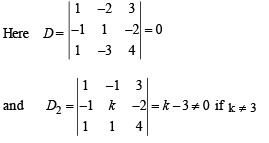
∴ If k ≠ 3 , the system has no solutions.
Hence statement-1 is true and statement-2 is a correct explanation for statement - 1.
Hence statement-1 is true and statement-2 is a correct explanation for statement - 1.
Chapter doubts & questions for Matrices and Determinants - 35 Years Chapter wise Previous Year Solved Papers for JEE 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Matrices and Determinants - 35 Years Chapter wise Previous Year Solved Papers for JEE in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup
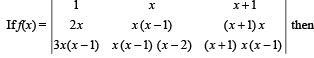




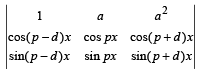 does not depend upon is
does not depend upon is


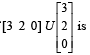

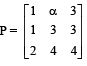 is the adjoint of a 3 × 3 matrix A and |A| = 4, then α is equal to :
is the adjoint of a 3 × 3 matrix A and |A| = 4, then α is equal to :
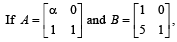 hen value of α for which A2 = B, is
hen value of α for which A2 = B, is

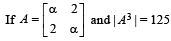 then the value of α is
then the value of α is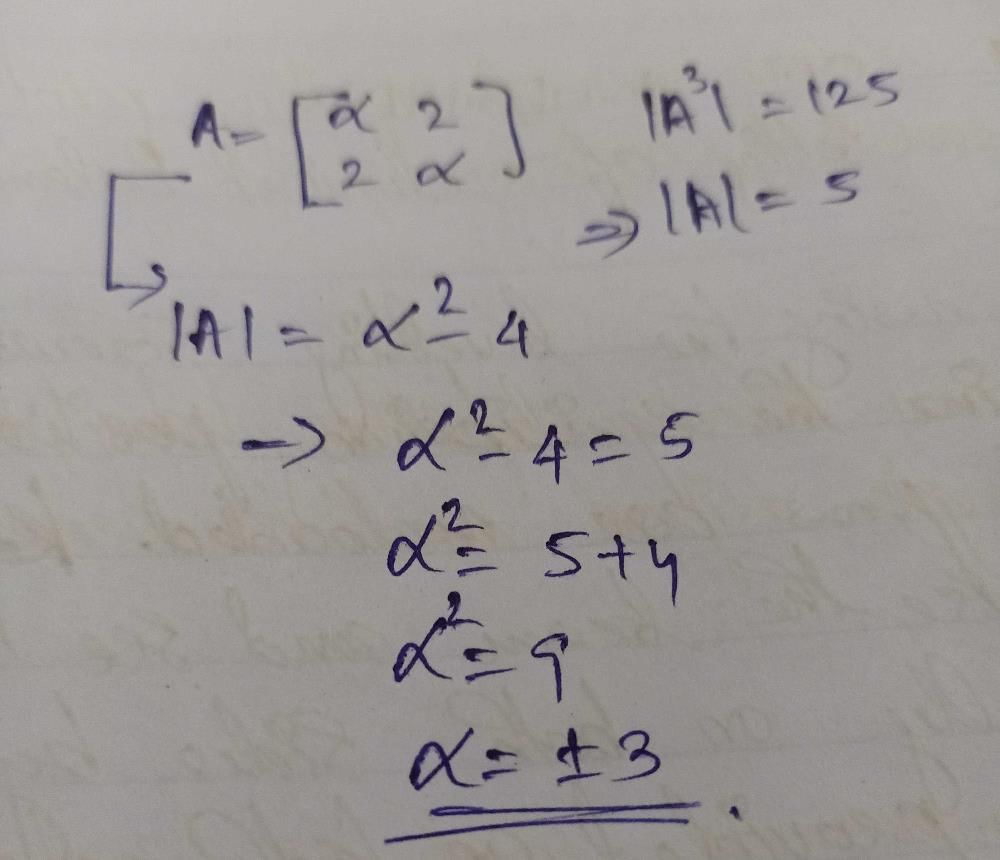
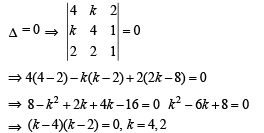
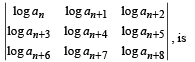

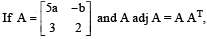 then 5a + b is equalto :
then 5a + b is equalto :