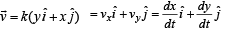All Exams >
JEE >
35 Years Chapter wise Previous Year Solved Papers for JEE >
All Questions
All questions of Motion for JEE Exam
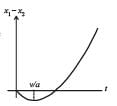
A body is at rest at x = 0. At t = 0, it starts moving in the positive x-direction with a constant acceleration. At the same instant another body passes through x = 0 moving in the positive x-direction with a constant speed. The position of the first body is given by x1(t) after time ‘t’; and that of the second body by x2(t) after the same time interval. Which of the following graphs correctly describes (x1 – x2) as a function of time ‘t’?- a)
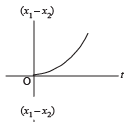
- b)
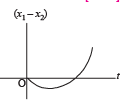
- c)
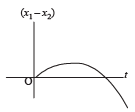
- d)
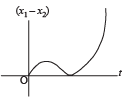
Correct answer is option 'B'. Can you explain this answer?
A body is at rest at x = 0. At t = 0, it starts moving in the positive x-direction with a constant acceleration. At the same instant another body passes through x = 0 moving in the positive x-direction with a constant speed. The position of the first body is given by x1(t) after time ‘t’; and that of the second body by x2(t) after the same time interval. Which of the following graphs correctly describes (x1 – x2) as a function of time ‘t’?
a)
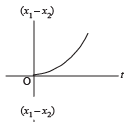
b)

c)

d)

|
|
Krishna Iyer answered |
For the body starting from rest
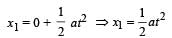
For the body moving with constant speed
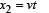
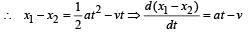

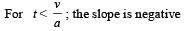
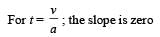
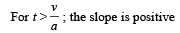
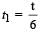
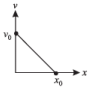
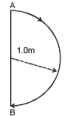
A boy playing on the roof of a 10 m high building throws a ball with a speed of 10m/s at an angle of 30º with the horizontal. How far from the throwing point will the ball be at the height of 10 m from the ground ?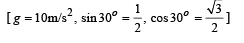
- a)5.20m
- b)4.33m
- c)2.60m
- d)8.66m
Correct answer is option 'D'. Can you explain this answer?
A boy playing on the roof of a 10 m high building throws a ball with a speed of 10m/s at an angle of 30º with the horizontal. How far from the throwing point will the ball be at the height of 10 m from the ground ?
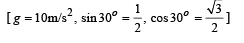
a)
5.20m
b)
4.33m
c)
2.60m
d)
8.66m

|
Ishanya Singh answered |

Two cars of mass m1 and m2 are moving in circles of radii r1 and r2, respectively. Their speeds are such that they make complete circles in the same time t. The ratio of their centripetal acceleration is :- a)m1r1 : m2r2
- b)m1 : m2
- c)r1 : r2
- d)1 : 1
Correct answer is option 'C'. Can you explain this answer?
Two cars of mass m1 and m2 are moving in circles of radii r1 and r2, respectively. Their speeds are such that they make complete circles in the same time t. The ratio of their centripetal acceleration is :
a)
m1r1 : m2r2
b)
m1 : m2
c)
r1 : r2
d)
1 : 1
|
|
Ankit Singh answered |

A car, moving with a speed of 50 km/hr, can be stopped by brakes after at least 6 m. If the same car is moving at a speed of 100 km/hr, the minimum stopping distance is- a)12 m
- b)18 m
- c)24 m
- d)6 m
Correct answer is option 'C'. Can you explain this answer?
A car, moving with a speed of 50 km/hr, can be stopped by brakes after at least 6 m. If the same car is moving at a speed of 100 km/hr, the minimum stopping distance is
a)
12 m
b)
18 m
c)
24 m
d)
6 m

|
Sinjini Datta answered |
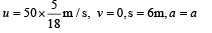
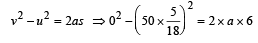
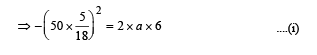
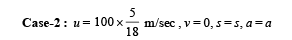
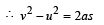
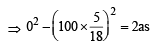
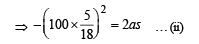
Dividing (i) and (ii) we get
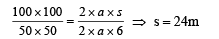
A car, starting from rest, accelerates at the rate f through a distance S, then continues at constant speed for time t and then decelerates at the rate f/2 to come to rest. If the total distance traversed is 15 S , then- a)
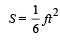
- b)
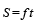
- c)

- d)
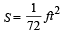
Correct answer is option 'D'. Can you explain this answer?
A car, starting from rest, accelerates at the rate f through a distance S, then continues at constant speed for time t and then decelerates at the rate f/2 to come to rest. If the total distance traversed is 15 S , then
a)
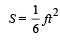
b)
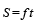
c)

d)
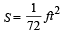
|
|
Yash Patel answered |
Distance from A to B = S = 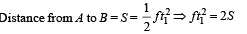
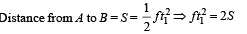

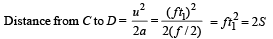

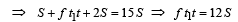

On dividing the above two equations, we get 
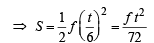

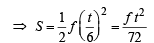
The coordinates of a particle moving in a plane are given by x(t) = a cos (pt) and y (t) = b sin (pt) where a, b (< a) and p are positive constants of appropriate dimensions. Then- a)the path of the particle is an ellipse
- b)the velocity and acceleration of the particle are normal to each other at t =π/(2p)
- c) the acceler ation of the particle is always directed towards a focus
- d)the distance travelled by the particle in time interval t = 0 tot =π/(2p) is a
Correct answer is option 'A,B,C'. Can you explain this answer?
The coordinates of a particle moving in a plane are given by x(t) = a cos (pt) and y (t) = b sin (pt) where a, b (< a) and p are positive constants of appropriate dimensions. Then
a)
the path of the particle is an ellipse
b)
the velocity and acceleration of the particle are normal to each other at t =π/(2p)
c)
the acceler ation of the particle is always directed towards a focus
d)
the distance travelled by the particle in time interval t = 0 tot =π/(2p) is a
|
|
Rounak Verma answered |
>0) and p (>0) are constants.
To find the velocity of the particle, we need to take the derivatives of x(t) and y(t) with respect to time t:
dx/dt = -a p sin (pt)
dy/dt = b p cos (pt)
The velocity of the particle is the vector (dx/dt, dy/dt), which can be written as:
v(t) = (-a p sin (pt), b p cos (pt))
To find the speed of the particle, we need to find the magnitude of the velocity vector:
|v(t)| = sqrt((-a p sin (pt))^2 + (b p cos (pt))^2)
= sqrt(a^2 p^2 sin^2 (pt) + b^2 p^2 cos^2 (pt))
= p sqrt(a^2 sin^2 (pt) + b^2 cos^2 (pt))
Since p, a, and b are constants, the speed of the particle depends only on t and the values of a and b:
speed = |v(t)| = p sqrt(a^2 sin^2 (pt) + b^2 cos^2 (pt))
To find the velocity of the particle, we need to take the derivatives of x(t) and y(t) with respect to time t:
dx/dt = -a p sin (pt)
dy/dt = b p cos (pt)
The velocity of the particle is the vector (dx/dt, dy/dt), which can be written as:
v(t) = (-a p sin (pt), b p cos (pt))
To find the speed of the particle, we need to find the magnitude of the velocity vector:
|v(t)| = sqrt((-a p sin (pt))^2 + (b p cos (pt))^2)
= sqrt(a^2 p^2 sin^2 (pt) + b^2 p^2 cos^2 (pt))
= p sqrt(a^2 sin^2 (pt) + b^2 cos^2 (pt))
Since p, a, and b are constants, the speed of the particle depends only on t and the values of a and b:
speed = |v(t)| = p sqrt(a^2 sin^2 (pt) + b^2 cos^2 (pt))
A ball whose kinetic energy is E, is projected at an angle of 45° to the horizontal. The kinetic energy of the ball at the highest point of its flight will be- a)E
- b)E /√2
- c)E/2
- d)zero.
Correct answer is option 'C'. Can you explain this answer?
A ball whose kinetic energy is E, is projected at an angle of 45° to the horizontal. The kinetic energy of the ball at the highest point of its flight will be
a)
E
b)
E /√2
c)
E/2
d)
zero.

|
Avi Chawla answered |
Let u be the speed with which the ball of mass m is projected. Then the kinetic energy (E) at the point of projection is

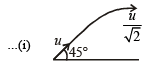

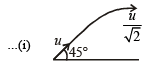
When the ball is at the highest point of its flight, the speed of the ball is 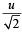 (Remember that the horizontal component of velocity does not change during a projectile motion).
(Remember that the horizontal component of velocity does not change during a projectile motion).
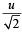 (Remember that the horizontal component of velocity does not change during a projectile motion).
(Remember that the horizontal component of velocity does not change during a projectile motion).∴ The kinetic energy at the highest point
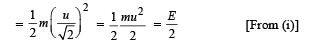
A ball is released from the top of a tower of height h meters.
It takes T seconds to reach the ground. What is the position of the ball at t/3
second- a)8h/9 meters from the ground
- b)7h/9 meters from the ground
- c)h/9 meters from the ground
- d)17h/18 meters from the ground
Correct answer is option 'A'. Can you explain this answer?
A ball is released from the top of a tower of height h meters.
It takes T seconds to reach the ground. What is the position of the ball at t/3
second
It takes T seconds to reach the ground. What is the position of the ball at t/3
second
a)
8h/9 meters from the ground
b)
7h/9 meters from the ground
c)
h/9 meters from the ground
d)
17h/18 meters from the ground

|
Akash Shah answered |
We know that now for T/3 second, vertical  distance moved is given by
distance moved is given by
 distance moved is given by
distance moved is given by
∴ position of ball from ground 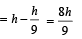
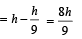
From a tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle, to hit the ground, is n times that taken by it to reach the highest point of its path. The relation between H, u and n is:- a)2gH = n 2 u2
- b)gH = ( n- 2 )2u 2
- c)2gH = nu 2 n- 2
- d)gH = ( n- 2)u 2
Correct answer is option 'C'. Can you explain this answer?
From a tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle, to hit the ground, is n times that taken by it to reach the highest point of its path. The relation between H, u and n is:
a)
2gH = n 2 u2
b)
gH = ( n- 2 )2u 2
c)
2gH = nu 2 n- 2
d)
gH = ( n- 2)u 2

|
Sanchita Iyer answered |
Ans.
Option (c)
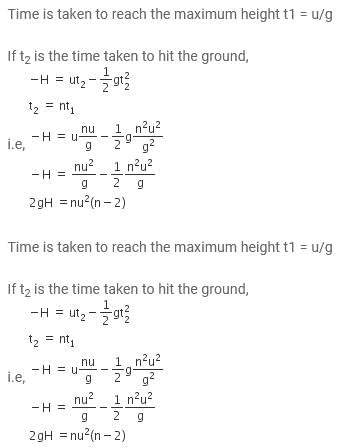
A projectile can have the same range ‘R’ for two angles of projection. If ‘T1’ and ‘T2’ to be time of flights in the two cases, then the product of the two time of flights is directly proportional to.- a)R
- b)1/R
- c) 1/R2
- d)R 2
Correct answer is option 'A'. Can you explain this answer?
A projectile can have the same range ‘R’ for two angles of projection. If ‘T1’ and ‘T2’ to be time of flights in the two cases, then the product of the two time of flights is directly proportional to.
a)
R
b)
1/R
c)
1/R2
d)
R 2
|
|
Palak Joshi answered |
A projectile can have the same range if launched at different angles but with the same initial speed. This is because the range of a projectile is determined by the horizontal component of its initial velocity, while the vertical component only affects the time of flight and the maximum height reached.
For example, if a projectile is launched at an angle of 30 degrees with an initial speed of 10 m/s, it will have a certain range. If the projectile is then launched at an angle of 60 degrees but with the same initial speed of 10 m/s, it will also have the same range. This is because the horizontal components of the initial velocities are the same in both cases, resulting in the same range.
However, it's important to note that the trajectories of the projectiles will be different. The projectile launched at a steeper angle will have a higher maximum height and a longer time of flight compared to the projectile launched at a shallower angle.
For example, if a projectile is launched at an angle of 30 degrees with an initial speed of 10 m/s, it will have a certain range. If the projectile is then launched at an angle of 60 degrees but with the same initial speed of 10 m/s, it will also have the same range. This is because the horizontal components of the initial velocities are the same in both cases, resulting in the same range.
However, it's important to note that the trajectories of the projectiles will be different. The projectile launched at a steeper angle will have a higher maximum height and a longer time of flight compared to the projectile launched at a shallower angle.
The relation between time t and distance x is t = ax 2 + bx where a and b are constants. The acceleration is - a)2bv 3
- b)-2abv2
- c)2av2
- d)-2av3
Correct answer is option 'D'. Can you explain this answer?
The relation between time t and distance x is t = ax 2 + bx where a and b are constants. The acceleration is
a)
2bv 3
b)
-2abv2
c)
2av2
d)
-2av3
|
|
Gowri Tiwari answered |
The relation between time t and distance x is given by the equation t = ax^2 + bx, where a and b are constants. We are asked to find the acceleration.
To find the acceleration, we need to differentiate the equation of motion with respect to time. Let's differentiate both sides of the equation:
d/dt (t) = d/dt (ax^2 + bx)
On the left-hand side, the derivative of t with respect to t is simply 1. On the right-hand side, we need to apply the chain rule. The derivative of ax^2 with respect to t is 2ax * dx/dt, and the derivative of bx with respect to t is b * dx/dt.
So, we have:
1 = 2ax * dx/dt + b * dx/dt
Now, let's solve for dx/dt, which represents the velocity v:
dx/dt = 1 / (2ax + b)
To find the acceleration, we need to differentiate the velocity equation with respect to time:
d/dt (dx/dt) = d/dt (1 / (2ax + b))
Using the chain rule, the derivative of 1 / (2ax + b) with respect to t is:
-2a / (2ax + b)^2 * dx/dt
Substituting the value of dx/dt from the velocity equation, we get:
-2a / (2ax + b)^2 * (1 / (2ax + b))
Simplifying this expression, we have:
-2a / (2ax + b)^3
Thus, the acceleration is given by -2a / (2ax + b)^3.
Comparing this with the given answer options, we can see that the correct answer is option 'D': -2av^3.
To find the acceleration, we need to differentiate the equation of motion with respect to time. Let's differentiate both sides of the equation:
d/dt (t) = d/dt (ax^2 + bx)
On the left-hand side, the derivative of t with respect to t is simply 1. On the right-hand side, we need to apply the chain rule. The derivative of ax^2 with respect to t is 2ax * dx/dt, and the derivative of bx with respect to t is b * dx/dt.
So, we have:
1 = 2ax * dx/dt + b * dx/dt
Now, let's solve for dx/dt, which represents the velocity v:
dx/dt = 1 / (2ax + b)
To find the acceleration, we need to differentiate the velocity equation with respect to time:
d/dt (dx/dt) = d/dt (1 / (2ax + b))
Using the chain rule, the derivative of 1 / (2ax + b) with respect to t is:
-2a / (2ax + b)^2 * dx/dt
Substituting the value of dx/dt from the velocity equation, we get:
-2a / (2ax + b)^2 * (1 / (2ax + b))
Simplifying this expression, we have:
-2a / (2ax + b)^3
Thus, the acceleration is given by -2a / (2ax + b)^3.
Comparing this with the given answer options, we can see that the correct answer is option 'D': -2av^3.
From a building two balls A and B are thrown such that A is thrown upwards and B downwards (both vertically with the same speed). If vA and vB are their respective velocities on reaching the ground, then- a)vB > vA
- b) vA = vB
- c)vA > vB
- d)(d) their velocities depend on their masses.
Correct answer is option 'B'. Can you explain this answer?
From a building two balls A and B are thrown such that A is thrown upwards and B downwards (both vertically with the same speed). If vA and vB are their respective velocities on reaching the ground, then
a)
vB > vA
b)
vA = vB
c)
vA > vB
d)
(d) their velocities depend on their masses.

|
Akash Shah answered |
Ball A is thrown upwards from the building. During its downward journey when it comes back to the point of throw, its speed is equal to the speed of throw. So, for the journey of both the balls from point A to B .

We can apply v2 – u2 = 2gh.
As u, g, h are same for both the balls, vA = vB
An object, moving with a speed of 6.25 m/s, is decelerated at a rate given by: dv/dt =-2.5√v
where v is the instantaneous speed. The timetaken by the object, to come to rest, would be:- a)2 s
- b)4 s
- c)8 s
- d)1 s
Correct answer is option 'A'. Can you explain this answer?
An object, moving with a speed of 6.25 m/s, is decelerated at a rate given by: dv/dt =-2.5√v
where v is the instantaneous speed. The timetaken by the object, to come to rest, would be:
where v is the instantaneous speed. The timetaken by the object, to come to rest, would be:
a)
2 s
b)
4 s
c)
8 s
d)
1 s
|
|
Pranavi Singh answered |
The object is decelerated at a rate of -2.5 m/s^2.
This means that the velocity of the object is decreasing by 2.5 m/s every second.
This means that the velocity of the object is decreasing by 2.5 m/s every second.
A river is flowing from west to east at a speed of 5 metres per minute. A man on the south bank of the river, capable of swimming at 10 metres per minute in still water, wants to swim across the river in the shortest time. He should swim in a direction- a)due north
- b)30° east of north
- c)30° west of north
- d)60° east of north
Correct answer is option 'A'. Can you explain this answer?
A river is flowing from west to east at a speed of 5 metres per minute. A man on the south bank of the river, capable of swimming at 10 metres per minute in still water, wants to swim across the river in the shortest time. He should swim in a direction
a)
due north
b)
30° east of north
c)
30° west of north
d)
60° east of north

|
Lekshmi Basu answered |
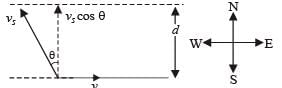
Time taken to cross the river t = d/v5cosθ
NOTE : For time to be minimum, cosθ = maximum⇒θ= 0°
The swimmer should swim due north.
A particle is projected at 60o to the horizontal with a kinetic energy K. The kinetic energy at the highest point is - a)K/2
- b)K
- c)Zero
- d)K/4
Correct answer is option 'D'. Can you explain this answer?
A particle is projected at 60o to the horizontal with a kinetic energy K. The kinetic energy at the highest point is
a)
K/2
b)
K
c)
Zero
d)
K/4

|
Sanchita Patel answered |
Let u be the velocity with which the particle is thrown and m be the mass of the particle. Then
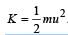
At the highest point the velocity is u cos 60° (only the horizontal component remains, the vertical component being zero at the top-most point). Therefore kinetic energy at the highest point.
A projectile is given an initial velocity of (iˆ + 2ˆj) m/s, where iˆ is along the ground and ˆj is along the vertical. If g = 10 m/s2 , the equation of its trajectory is : - a)y = x- 5x2
- b)y = 2 x-5x2
- c)4 y = 2 x-5x2
- d)4 y = 2 x- 25x2
Correct answer is option 'B'. Can you explain this answer?
A projectile is given an initial velocity of (iˆ + 2ˆj) m/s, where iˆ is along the ground and ˆj is along the vertical. If g = 10 m/s2 , the equation of its trajectory is :
a)
y = x- 5x2
b)
y = 2 x-5x2
c)
4 y = 2 x-5x2
d)
4 y = 2 x- 25x2

|
Pragati Nair answered |
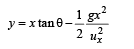
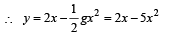
Two stones are thrown up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graph best represents the time variation of relative position of the second stone with respect to the first ? (Assume stones do not rebound after hitting the ground and neglect air resistance, take g = 10 m/ s2) (The figures are schematic and not drawn to scale)- a)
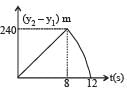
- b)
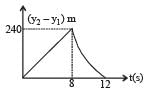
- c)
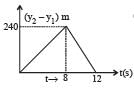
- d)
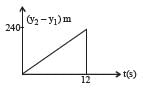
Correct answer is option 'B'. Can you explain this answer?
Two stones are thrown up simultaneously from the edge of a cliff 240 m high with initial speed of 10 m/s and 40 m/s respectively. Which of the following graph best represents the time variation of relative position of the second stone with respect to the first ? (Assume stones do not rebound after hitting the ground and neglect air resistance, take g = 10 m/ s2) (The figures are schematic and not drawn to scale)
a)

b)

c)

d)


|
Siddharth Chaudhary answered |

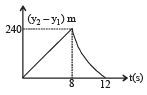
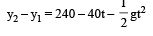
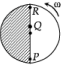
Consider a disc rotating in the horizontal plane with a constant angular speed w about its centre O. The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection is in the y-z plane and is same for both pebbles with respect to the disc. Assume that (i) they land back on the disc before the disc has completed 1/8 rotation, (ii) their range is less than half the disc radius, and (iii) w remains constant throughout. Then .
- a)P lands in the shaded region and Q in the unshaded region.
- b) P lands in the unshaded region and Q in the shaded region.
- c)Both P and Q land in the unshaded region.
- d)Both P and Q land in the shaded region.
Correct answer is option 'C'. Can you explain this answer?
Consider a disc rotating in the horizontal plane with a constant angular speed w about its centre O. The disc has a shaded region on one side of the diameter and an unshaded region on the other side as shown in the figure. When the disc is in the orientation as shown, two pebbles P and Q are simultaneously projected at an angle towards R. The velocity of projection is in the y-z plane and is same for both pebbles with respect to the disc. Assume that (i) they land back on the disc before the disc has completed 1/8 rotation, (ii) their range is less than half the disc radius, and (iii) w remains constant throughout. Then .

a)
P lands in the shaded region and Q in the unshaded region.
b)
P lands in the unshaded region and Q in the shaded region.
c)
Both P and Q land in the unshaded region.
d)
Both P and Q land in the shaded region.

|
Roshni Chavan answered |
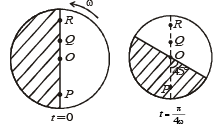
The x-coordinate of 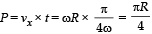
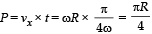
This horizontal distance travelled will be greater than any point on the disc between O and P. Therefore the landing will be in unshaded area. In the same way, the horizontal distance travelled by Q is always less than that of any point between O and R. Therefore the landing will be in unshaded area.
STATEMENT-1 : For an observer looking out through the window of a fast moving train, the nearby objects appear to move in the opposite direction to the train, while the distant objects appear to be stationary.
STATEMENT-2 : If the observer and the object are moving at velocities 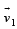 and
and 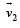 respectively with reference to a laboratory frame, the velocity of the object with respect to the observer is
respectively with reference to a laboratory frame, the velocity of the object with respect to the observer is 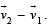 .
.
- a)Statement-1 is True, Statement-2 is True; Statement-2 is a correct explanation for Statement-1
- b)Statement1 is True, Statement-2 is True; Statement-2 is NOT a correct explanation for Statement-1
- c)Statement -1 is True, Statement-2 is False
- d)Statement -1 is False, Statement-2 is True
Correct answer is option 'B'. Can you explain this answer?
STATEMENT-1 : For an observer looking out through the window of a fast moving train, the nearby objects appear to move in the opposite direction to the train, while the distant objects appear to be stationary.
STATEMENT-2 : If the observer and the object are moving at velocities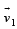 and
and 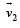 respectively with reference to a laboratory frame, the velocity of the object with respect to the observer is
respectively with reference to a laboratory frame, the velocity of the object with respect to the observer is 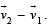 .
.
STATEMENT-2 : If the observer and the object are moving at velocities
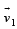 and
and 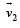 respectively with reference to a laboratory frame, the velocity of the object with respect to the observer is
respectively with reference to a laboratory frame, the velocity of the object with respect to the observer is 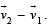 .
.a)
Statement-1 is True, Statement-2 is True; Statement-2 is a correct explanation for Statement-1
b)
Statement1 is True, Statement-2 is True; Statement-2 is NOT a correct explanation for Statement-1
c)
Statement -1 is True, Statement-2 is False
d)
Statement -1 is False, Statement-2 is True

|
Siddharth Chaudhary answered |
Statement-1 is true. For a moving observer, the near by objects appear to move in the opposite direction at a large speed. This is because the angular speed of the near by object w.r.t observer is large. As the object moves away the angular velocity decreases and therefore its speed seems to be less. The distant object almost remains stationary.
Statement-2 is the concept of relative velocity which states that.
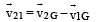
where G is the laboratory frame.
Thus both the statement are true but statement-2 is not the correct explanation of statement-1.
Thus both the statement are true but statement-2 is not the correct explanation of statement-1.
Which of the following statements is FALSE for a particle moving in a circle with a constant angular speed ?- a)The acceleration vector points to the centre of the circle
- b)The acceleration vector is tangent to the circle
- c)The velocity vector is tangent to the circle
- d) The velocity and acceleration vectors are perpendicular to each other.
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements is FALSE for a particle moving in a circle with a constant angular speed ?
a)
The acceleration vector points to the centre of the circle
b)
The acceleration vector is tangent to the circle
c)
The velocity vector is tangent to the circle
d)
The velocity and acceleration vectors are perpendicular to each other.

|
Avi Chawla answered |
Only option (b) is false since acceleration vector is always radial (i.e . towards the center) for uniform circular motion.
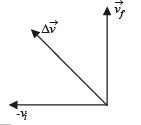
A particle is moving eastwards with a velocity of 5 m/s. In 10s the velocity changes to 5 m/s northwards. The average acceleration in this time is- a)zero
- b)1√2 m/s2 towards north-west
- c)1 /√2m/s2 towards north-east
- d)1 / 2m/s2 towards north-west
- e)1 / 2m/s2 towards north
Correct answer is option 'B'. Can you explain this answer?
A particle is moving eastwards with a velocity of 5 m/s. In 10s the velocity changes to 5 m/s northwards. The average acceleration in this time is
a)
zero
b)
1√2 m/s2 towards north-west
c)
1 /√2m/s2 towards north-east
d)
1 / 2m/s2 towards north-west
e)
1 / 2m/s2 towards north

|
Roshni Chavan answered |
Average acceleration
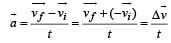
To find the resultant of  and
and  , we draw a diagram
, we draw a diagram
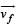 and
and 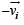 , we draw a diagram
, we draw a diagram 
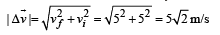
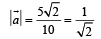
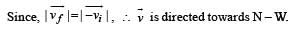
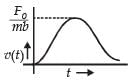
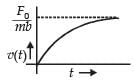
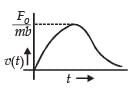
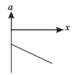
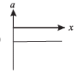
A body starts from rest at time t = 0, the acceleration time graph is shown in the figure. The maximum velocity attained by the body will be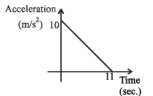
- a)110 m/s
- b) 55 m/s
- c) 650 m/s
- d)550 m/s
Correct answer is option 'B'. Can you explain this answer?
A body starts from rest at time t = 0, the acceleration time graph is shown in the figure. The maximum velocity attained by the body will be

a)
110 m/s
b)
55 m/s
c)
650 m/s
d)
550 m/s

|
Aryan Sen answered |
Change in velocity = area under the graph
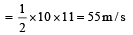
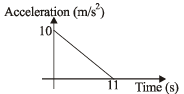
Since, initial velocity is zero, final velocity is 55 m/s.
A boat which has a speed of 5 km/hr in still water crosses a river of width 1 km along the shortest possible path in 15 minutes. The velocity of the river water in km/hr is- a)1
- b)3
- c)4
- d)
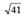
Correct answer is option 'B'. Can you explain this answer?
A boat which has a speed of 5 km/hr in still water crosses a river of width 1 km along the shortest possible path in 15 minutes. The velocity of the river water in km/hr is
a)
1
b)
3
c)
4
d)
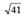

|
Nilesh Saini answered |
Shortest route corresponds to vrb perpendicular to river flow
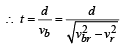
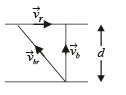
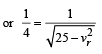
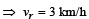
A particle of mass m moves on the x-axis as follows : it starts from rest at t = 0 from the point x = 0, and comes to rest at t = 1 at the point x = 1. NO other information is available about its motion at intermediate times (0 < t< 1). If a denotes the instantaneous acceleration of the particle, then:- a)a cann ot rem ai n posit ive for al l t in the interval
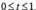
- b)|α| cannot exceed 2 at any point in its path.
- c)|α| must be
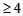 at some point or points in its path.
at some point or points in its path. - d)α must change sign during the motion, but no other assertion can be made with the information given.
Correct answer is option 'A,C,D'. Can you explain this answer?
A particle of mass m moves on the x-axis as follows : it starts from rest at t = 0 from the point x = 0, and comes to rest at t = 1 at the point x = 1. NO other information is available about its motion at intermediate times (0 < t< 1). If a denotes the instantaneous acceleration of the particle, then:
a)
a cann ot rem ai n posit ive for al l t in the interval 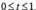
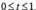
b)
|α| cannot exceed 2 at any point in its path.
c)
|α| must be 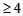 at some point or points in its path.
at some point or points in its path.
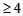 at some point or points in its path.
at some point or points in its path.d)
α must change sign during the motion, but no other assertion can be made with the information given.

|
Aryan Sen answered |
Note : a cannot remain positive for all t in the interval 0 < t < 1. This is because since the body starts from rest, it will first accelerate. Finally it stops therefore a will become negative. Therefore a will change its direction. Options (a) and (d) are correct.
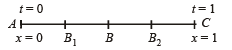
Let the particle accelerate uniformly till half the distance (A to B) and then retard uniformly in the remaining half distance (B to C).
The total time is 1 sec. Therefore the time taken from A to B is 0.5 sec.
For A to B
The total time is 1 sec. Therefore the time taken from A to B is 0.5 sec.
For A to B
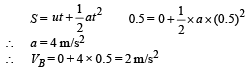
Note : Now, if the particle accelerates till B2 then for covering the same total distance in same time, acceleration should be less than 4 m/s2 but |deceleration| should be greater than 4 m/s2. And if the particle accelerates till B1, then for covering the same total distance in the same time, the acceleration should be greater than 4 m/s2 and | deceleration | < 4 m/s2.
The same is depicted by the graph.
The same is depicted by the graph.
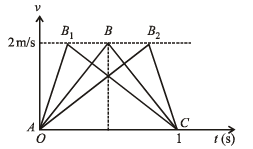
So, the | acceleration | must be greater than or equal to 4 m/s2 at some point or points in the path.
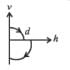
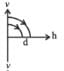
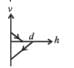
A ball is dropped vertically from a height d above the ground.
It hits the ground and bounces up vertically to a height d/2.
Neglecting subsequent motion and air resistance, its velocity v varies with the height h above the ground as - a)
- b)
- c)
- d)
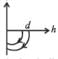
Correct answer is option 'A'. Can you explain this answer?
A ball is dropped vertically from a height d above the ground.
It hits the ground and bounces up vertically to a height d/2.
Neglecting subsequent motion and air resistance, its velocity v varies with the height h above the ground as
It hits the ground and bounces up vertically to a height d/2.
Neglecting subsequent motion and air resistance, its velocity v varies with the height h above the ground as
a)

b)

c)

d)


|
Roshni Chavan answered |
(a) KEY CONCEPT Before hitting the ground, the velocity v is given by v2 = 2 gd (quadratic equation and hence parabolic path) Downwards direction means negative velocity. After collision, the direction become positive and velocity decreases.
Further,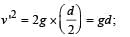
Further,
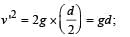
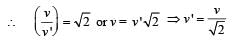
Consider a rubber ball freely falling from a height h = 4.9 m onto a horizontal elastic plate. Assume that the duration of collision is negligible and the collision with the plate is totally elastic.
Then the velocity as a function of time and the height as a function of time will be : - a)
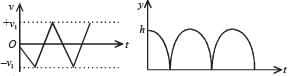
- b)

- c)

- d)
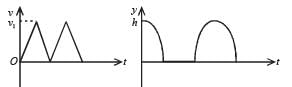
Correct answer is option 'B'. Can you explain this answer?
Consider a rubber ball freely falling from a height h = 4.9 m onto a horizontal elastic plate. Assume that the duration of collision is negligible and the collision with the plate is totally elastic.
Then the velocity as a function of time and the height as a function of time will be :
Then the velocity as a function of time and the height as a function of time will be :
a)

b)

c)

d)

|
|
Gowri Tiwari answered |
For downward motion v = –gt The velocity of the rubber ball increases in downward direction and we get a straight line between v and t with a negative slope.

The graph between y and t is a parabola with y = h at t = 0. As time increases y decreases.
For upward motion.
The ball suffer elastic collision with the horizontal elastic plate therefore the direction of velocity is reversed and the magnitude remains the same.
Here v = u – gt where u is the velocity just after collision.
As t increases, v decreases. We get a straight line between v and t with negative slope.
The ball suffer elastic collision with the horizontal elastic plate therefore the direction of velocity is reversed and the magnitude remains the same.
Here v = u – gt where u is the velocity just after collision.
As t increases, v decreases. We get a straight line between v and t with negative slope.
All these characteristics are represented by graph (b).
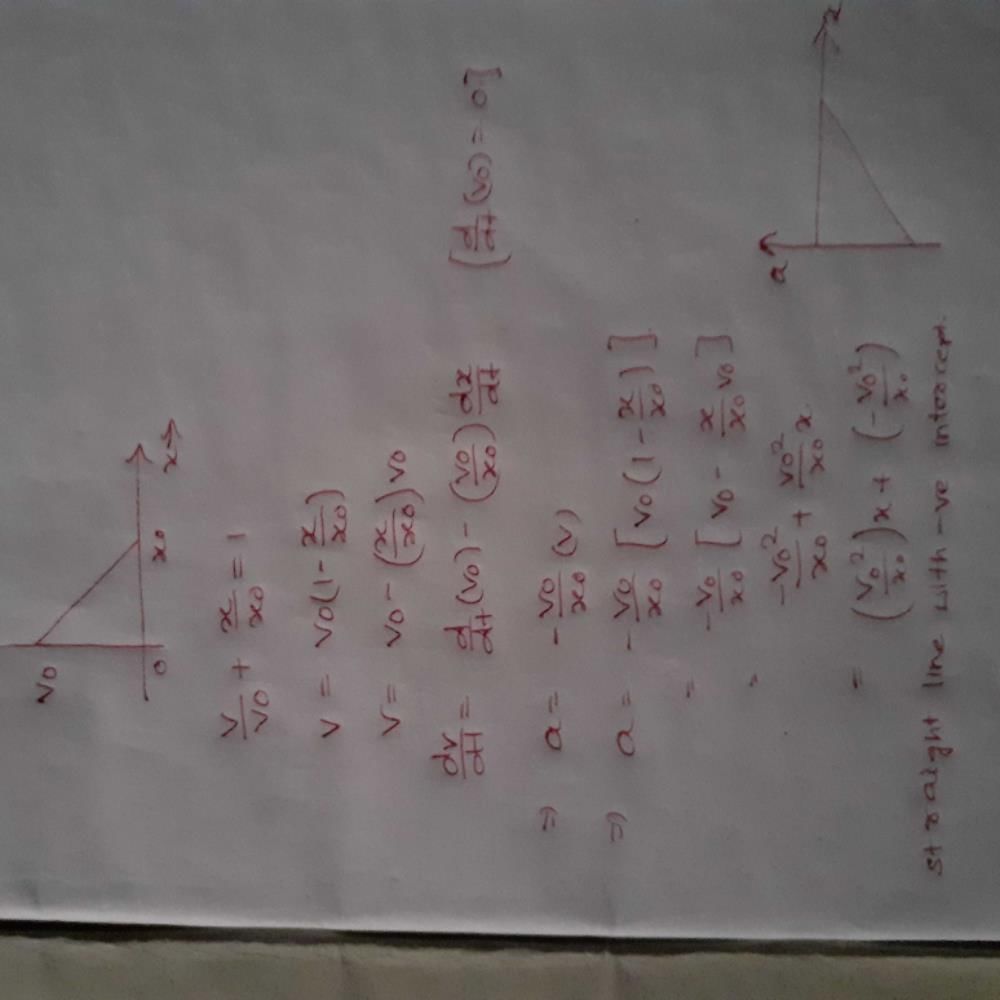
A ball is thrown from a point with a speed ' v0' at an elevation angle of q. From the same point and at the same instant, a person starts running with a constant speed ' 
to catch the ball. Will the person be able to catch the ball? If yes, what should be the angle of projection θ?- a)No
- b)Yes, 30°
- c)Yes, 60°
- d)Yes, 45°
Correct answer is option 'C'. Can you explain this answer?
A ball is thrown from a point with a speed ' v0' at an elevation angle of q. From the same point and at the same instant, a person starts running with a constant speed ' 
to catch the ball. Will the person be able to catch the ball? If yes, what should be the angle of projection θ?

to catch the ball. Will the person be able to catch the ball? If yes, what should be the angle of projection θ?
a)
No
b)
Yes, 30°
c)
Yes, 60°
d)
Yes, 45°

|
Pragati Nair answered |
Yes, the person can catch the ball when horizontal velocity is equal to the horizontal component of ball’s velocity, the motion of ball will be only in vertical direction with respect to person for that,
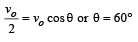
A point P moves in counter-clockwise direction on a circular path as shown in the figure. The movement of 'P' is such that it sweeps out a length s = t3 + 5, where s is in metres and t is in seconds. The radius of the path is 20 m. The acceleration of 'P' when t = 2 s is nearly.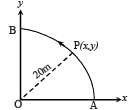
- a) 13m/s2
- b)12 m/s2
- c)7.2 ms2
- d)14m/s2
Correct answer is option 'D'. Can you explain this answer?
A point P moves in counter-clockwise direction on a circular path as shown in the figure. The movement of 'P' is such that it sweeps out a length s = t3 + 5, where s is in metres and t is in seconds. The radius of the path is 20 m. The acceleration of 'P' when t = 2 s is nearly.

a)
13m/s2
b)
12 m/s2
c)
7.2 ms2
d)
14m/s2

|
Sinjini Datta answered |
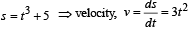
Tangential acceleration 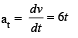
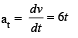
Radial acceleration 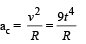
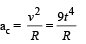
At t = 2s, at = 6 ´ 2= 12 m/s2
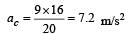
∴ Resultant acceleration

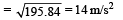
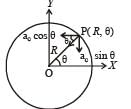
A small particle of mass m is projected at an angle q with the x-axis with an initial velocity v0 in the x-y plane as shown in the figure. At a time 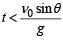 the angular momentum of the particle is
the angular momentum of the particle is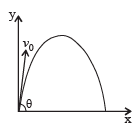 where iˆ,ˆj and kˆ are unit vectors along x, y and z-axis respectively.
where iˆ,ˆj and kˆ are unit vectors along x, y and z-axis respectively. - a)

- b)
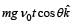
- c)
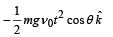
- d)
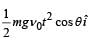
Correct answer is option 'C'. Can you explain this answer?
A small particle of mass m is projected at an angle q with the x-axis with an initial velocity v0 in the x-y plane as shown in the figure. At a time 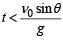 the angular momentum of the particle is
the angular momentum of the particle is
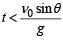 the angular momentum of the particle is
the angular momentum of the particle is
where iˆ,ˆj and kˆ are unit vectors along x, y and z-axis respectively.
a)

b)
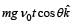
c)
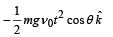
d)
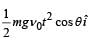

|
Akash Shah answered |
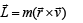
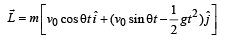
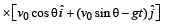
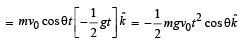
A particle is moving eastwards with a velocity of 5 ms -1 . In 10 seconds the velocity changes to 5 ms-1 northwards.
The average acceleration in this time is- a)
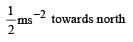
- b)
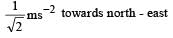
- c)

- d)zero
Correct answer is option 'C'. Can you explain this answer?
A particle is moving eastwards with a velocity of 5 ms -1 . In 10 seconds the velocity changes to 5 ms-1 northwards.
The average acceleration in this time is
The average acceleration in this time is
a)
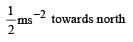
b)
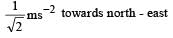
c)

d)
zero

|
Aryan Dasgupta answered |
Average acceleration 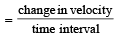
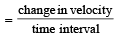
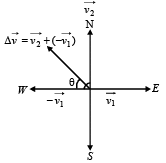
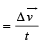

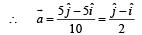
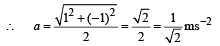
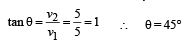
Therefore the directon is North-west.
Two identical discs of same radius R are rotating about their axes in opposite directions with the same constant angular speed w. The discs are in the same horizontal plane. At time t = 0, the points P and Q are facing each other as shown in the figure. The relative speed between the two points P and Q is vr. In one time period (T) of rotation of the discs, vr as a function of time is best represented by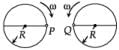
- a)

- b)
- c)

- d)
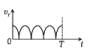
Correct answer is option 'A'. Can you explain this answer?
Two identical discs of same radius R are rotating about their axes in opposite directions with the same constant angular speed w. The discs are in the same horizontal plane. At time t = 0, the points P and Q are facing each other as shown in the figure. The relative speed between the two points P and Q is vr. In one time period (T) of rotation of the discs, vr as a function of time is best represented by

a)

b)
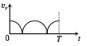
c)

d)


|
Pragati Dey answered |
At t = 0, the relative velocity will be zero.
At 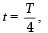 , the relative velocity will be maximum in magnitude.
, the relative velocity will be maximum in magnitude.
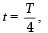 , the relative velocity will be maximum in magnitude.
, the relative velocity will be maximum in magnitude.At 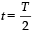 , the relative velocity will be zero.
, the relative velocity will be zero.
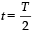 , the relative velocity will be zero.
, the relative velocity will be zero.At  , the relative velocity will be maximum in magnitude
, the relative velocity will be maximum in magnitude
 , the relative velocity will be maximum in magnitude
, the relative velocity will be maximum in magnitudeAt t = T, the relative velocity again becomes zero.
Chapter doubts & questions for Motion - 35 Years Chapter wise Previous Year Solved Papers for JEE 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Motion - 35 Years Chapter wise Previous Year Solved Papers for JEE in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup





 .
.
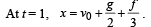



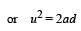
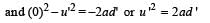
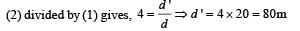
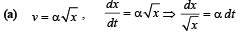
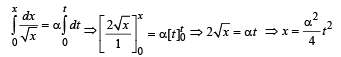
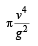
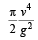
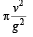
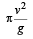
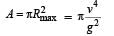
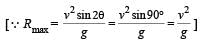
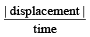
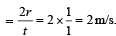
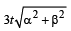

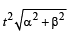
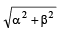
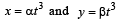
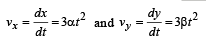
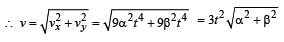
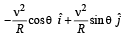

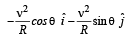

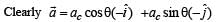
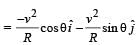
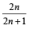
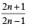

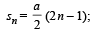
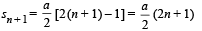
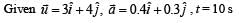


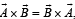 then the angle between A and B is
then the angle between A and B is
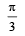

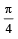
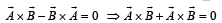


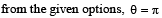
 , where k is a constant. The general equation for its path is
, where k is a constant. The general equation for its path is