All Exams >
SSC CGL >
SSC CGL Previous Year Papers >
All Questions
All questions of Average for SSC CGL Exam
Average of first five prime numbers is (SSC Multitasking 2013)- a)3.6
- b)5.3
- c)5.6
- d)5
Correct answer is option 'C'. Can you explain this answer?
Average of first five prime numbers is (SSC Multitasking 2013)
a)
3.6
b)
5.3
c)
5.6
d)
5
|
Ssc Cgl answered |
First five prime numbers are 2, 3, 5, 7, 11
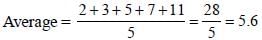
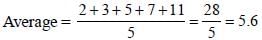
The average marks obtained by a class of 60 students is 65. The average marks of half of the students is found to be 85.The average marks of the remaining students is (SSC CGL 2nd Sit. 2016)- a)35
- b)45
- c)55
- d)65
Correct answer is option 'B'. Can you explain this answer?
The average marks obtained by a class of 60 students is 65. The average marks of half of the students is found to be 85.The average marks of the remaining students is (SSC CGL 2nd Sit. 2016)
a)
35
b)
45
c)
55
d)
65
|
Mira Sharma answered |
Total students = 60
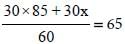
30x = 65 × 60 – 30 × 85
30x = 30[65 × 2 – 85]
x = 30/30[130-85] = 45
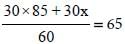
30x = 65 × 60 – 30 × 85
30x = 30[65 × 2 – 85]
x = 30/30[130-85] = 45
The average of 17 results is 60. If the average of first 9 results is 57 and that of the last 9 results is 65, then what will be the value of 9th result? (SSC CGL 2017)- a)39
- b)78
- c)117
- d)156
Correct answer is option 'B'. Can you explain this answer?
The average of 17 results is 60. If the average of first 9 results is 57 and that of the last 9 results is 65, then what will be the value of 9th result? (SSC CGL 2017)
a)
39
b)
78
c)
117
d)
156
|
Iq Funda answered |
Value of 9th result = (9×57+9×65) – (17×60)
= 1098 – 1020
= 78
= 1098 – 1020
= 78
Out of 10 teachers of a school, one teacher retires and in his place, a new teacher of age 25 years joins. As a result, average age of teachers is reduced by 3 years. The age (in years) of the retired teacher is : (SSC CGL 1st Sit. 2013)- a)50
- b)58
- c)60
- d)55
Correct answer is option 'D'. Can you explain this answer?
Out of 10 teachers of a school, one teacher retires and in his place, a new teacher of age 25 years joins. As a result, average age of teachers is reduced by 3 years. The age (in years) of the retired teacher is : (SSC CGL 1st Sit. 2013)
a)
50
b)
58
c)
60
d)
55
|
EduRev SSC CGL answered |
Age of retired teacher = 25 + 3 × 10 = 55 years
The average of 18 numbers is 52. The average of the first 8 numbers is 62 and the average of the next 7 numbers is 45. If the 16th number is 6 less than the 17th number and the 17th number is one more than the 18th nmber, then what is the average of the 16th and 18th numbers? (SSC Sub. Ins. 2018 )- a)40.5
- b)40
- c)39
- d)39.5
Correct answer is option 'A'. Can you explain this answer?
The average of 18 numbers is 52. The average of the first 8 numbers is 62 and the average of the next 7 numbers is 45. If the 16th number is 6 less than the 17th number and the 17th number is one more than the 18th nmber, then what is the average of the 16th and 18th numbers? (SSC Sub. Ins. 2018 )
a)
40.5
b)
40
c)
39
d)
39.5
|
Abhiram Mehra answered |
Given Information:
- Average of 18 numbers = 52
- Average of the first 8 numbers = 62
- Average of the next 7 numbers = 45
- 16th number = 17th number - 6
- 17th number = 18th number + 1
Solution:
- Total sum of 18 numbers = 18 * 52 = 936
- Total sum of first 8 numbers = 8 * 62 = 496
- Total sum of next 7 numbers = 7 * 45 = 315
- Total sum of the first 15 numbers = 496 + 315 = 811
Calculations:
- Sum of the 16th, 17th, and 18th numbers = 936 - 811 = 125
- Since 17th number = 18th number + 1, let's assume the 18th number = x
- So, 17th number = x + 1 and 16th number = x + 1 - 6 = x - 5
- Sum of 16th, 17th, and 18th numbers = (x - 5) + (x + 1) + x = 3x - 4
- Therefore, x = 41, so the 18th number = 41, 17th number = 42, and 16th number = 36
Find Average:
- Average of 16th and 18th numbers = (36 + 41) / 2 = 77 / 2 = 38.5
Hence, the average of the 16th and 18th numbers is 38.5.
- Average of 18 numbers = 52
- Average of the first 8 numbers = 62
- Average of the next 7 numbers = 45
- 16th number = 17th number - 6
- 17th number = 18th number + 1
Solution:
- Total sum of 18 numbers = 18 * 52 = 936
- Total sum of first 8 numbers = 8 * 62 = 496
- Total sum of next 7 numbers = 7 * 45 = 315
- Total sum of the first 15 numbers = 496 + 315 = 811
Calculations:
- Sum of the 16th, 17th, and 18th numbers = 936 - 811 = 125
- Since 17th number = 18th number + 1, let's assume the 18th number = x
- So, 17th number = x + 1 and 16th number = x + 1 - 6 = x - 5
- Sum of 16th, 17th, and 18th numbers = (x - 5) + (x + 1) + x = 3x - 4
- Therefore, x = 41, so the 18th number = 41, 17th number = 42, and 16th number = 36
Find Average:
- Average of 16th and 18th numbers = (36 + 41) / 2 = 77 / 2 = 38.5
Hence, the average of the 16th and 18th numbers is 38.5.
The mean of 50 numbers is 30. Later it was discovered that two entries were wrongly entered as 82 and 13 instead of 28 and 31. Find the correct mean. (SSC CGL 1st Sit. 2011)- a)36.12
- b)30.66
- c)29.28
- d)38.21
Correct answer is option 'C'. Can you explain this answer?
The mean of 50 numbers is 30. Later it was discovered that two entries were wrongly entered as 82 and 13 instead of 28 and 31. Find the correct mean. (SSC CGL 1st Sit. 2011)
a)
36.12
b)
30.66
c)
29.28
d)
38.21
|
Malavika Rane answered |
< b="" />Given Information:< />
- The mean of 50 numbers is 30.
- Two entries were wrongly entered as 82 and 13 instead of 28 and 31.
< b="" />To Find:< />
- The correct mean of the numbers.
< b="" />Solution:< />
To find the correct mean, we need to calculate the sum of all the numbers and then divide it by the total number of entries.
Let's denote the sum of the 50 numbers as S.
< b="" />Step 1:< />
Calculate the sum of the 50 numbers using the given mean.
Mean = Sum of numbers / Total number of entries
30 = S / 50
S = 30 * 50
S = 1500
< b="" />Step 2:< />
Adjust the sum by replacing the wrongly entered numbers with the correct ones.
Since the numbers 82 and 13 were wrongly entered as 28 and 31 respectively, we need to subtract the incorrect values and add the correct values to the sum.
S' = S - 82 - 13 + 28 + 31
S' = 1500 - 82 - 13 + 28 + 31
S' = 1500 - 82 - 13 + 59
S' = 1500 - 36 + 59
S' = 1500 + 23
S' = 1523
< b="" />Step 3:< />
Calculate the correct mean using the adjusted sum.
Mean' = S' / 50
Mean' = 1523 / 50
Mean' = 30.46
< b="" />Answer:< />
Therefore, the correct mean of the 50 numbers is 30.46, which is approximately equal to 29.28 (option C).
- The mean of 50 numbers is 30.
- Two entries were wrongly entered as 82 and 13 instead of 28 and 31.
< b="" />To Find:< />
- The correct mean of the numbers.
< b="" />Solution:< />
To find the correct mean, we need to calculate the sum of all the numbers and then divide it by the total number of entries.
Let's denote the sum of the 50 numbers as S.
< b="" />Step 1:< />
Calculate the sum of the 50 numbers using the given mean.
Mean = Sum of numbers / Total number of entries
30 = S / 50
S = 30 * 50
S = 1500
< b="" />Step 2:< />
Adjust the sum by replacing the wrongly entered numbers with the correct ones.
Since the numbers 82 and 13 were wrongly entered as 28 and 31 respectively, we need to subtract the incorrect values and add the correct values to the sum.
S' = S - 82 - 13 + 28 + 31
S' = 1500 - 82 - 13 + 28 + 31
S' = 1500 - 82 - 13 + 59
S' = 1500 - 36 + 59
S' = 1500 + 23
S' = 1523
< b="" />Step 3:< />
Calculate the correct mean using the adjusted sum.
Mean' = S' / 50
Mean' = 1523 / 50
Mean' = 30.46
< b="" />Answer:< />
Therefore, the correct mean of the 50 numbers is 30.46, which is approximately equal to 29.28 (option C).
The average of 5 members of a family is 24 years. If the youngest member is 8 years old, then what was the average age (in years) of the family at the time of the birth of the youngest member? (SSC CGL 2017)- a)16
- b)20
- c)24
- d)32
Correct answer is option 'B'. Can you explain this answer?
The average of 5 members of a family is 24 years. If the youngest member is 8 years old, then what was the average age (in years) of the family at the time of the birth of the youngest member? (SSC CGL 2017)
a)
16
b)
20
c)
24
d)
32
|
Vinod Mehta answered |
Required average age 
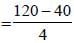= 80/4 = 20 years.
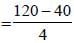= 80/4 = 20 years.The average monthly income of A and B is ₹15,050, the average monthly income of B and C is ₹15,350 and the average income of A and C is ₹15, 200. The monthly income of A is (SSC Sub. Ins. 2016)- a)₹15, 900
- b)₹15, 200
- c)₹14,900
- d)₹15,500
Correct answer is option 'C'. Can you explain this answer?
The average monthly income of A and B is ₹15,050, the average monthly income of B and C is ₹15,350 and the average income of A and C is ₹15, 200. The monthly income of A is (SSC Sub. Ins. 2016)
a)
₹15, 900
b)
₹15, 200
c)
₹14,900
d)
₹15,500
|
|
Iq Funda answered |
Sum of monthly income of A + B = 30100 ...(i)
Sum of monthly income of B + C = 30700 ...(ii)
Sum of monthly income of A + C = 30400 ...(iii)
Subtracting eqn. (i) from (ii)
B + C – A – B = 30700 – 30100
C – A = 600 ...(iv)
C + A = 30400 ...(v)
Subtracting eqn. (v) from (iv)
C – A – C – A = 600 – 30400 – 2A = – 29800
A = ₹14900
Sum of monthly income of B + C = 30700 ...(ii)
Sum of monthly income of A + C = 30400 ...(iii)
Subtracting eqn. (i) from (ii)
B + C – A – B = 30700 – 30100
C – A = 600 ...(iv)
C + A = 30400 ...(v)
Subtracting eqn. (v) from (iv)
C – A – C – A = 600 – 30400 – 2A = – 29800
A = ₹14900
Visitors to a show were charged ₹ 15 each on the first day, ₹ 7.50 on the second day, ₹ 2.50 on the third day and total attendance on three days were in the ratio 2:5:13 respectively. The average charge per person for the entire three days is (SSC CGL 2nd Sit. 2016)- a)₹ 5
- b)₹ 5.50
- c)₹ 6
- d)₹ 7
Correct answer is option 'A'. Can you explain this answer?
Visitors to a show were charged ₹ 15 each on the first day, ₹ 7.50 on the second day, ₹ 2.50 on the third day and total attendance on three days were in the ratio 2:5:13 respectively. The average charge per person for the entire three days is (SSC CGL 2nd Sit. 2016)
a)
₹ 5
b)
₹ 5.50
c)
₹ 6
d)
₹ 7
|
|
Abhiram Mehra answered |
Calculation of the average charge per person for the entire three days:
1. Calculate the total amount collected each day:
- On the first day: 15 * 2 = 30
- On the second day: 7.50 * 5 = 37.50
- On the third day: 2.50 * 13 = 32.50
2. Calculate the total attendance each day:
- Total attendance for three days = 2 + 5 + 13 = 20
3. Calculate the total amount collected over three days:
- Total amount collected = 30 + 37.50 + 32.50 = 100
4. Calculate the average charge per person for the entire three days:
- Average charge per person = Total amount collected / Total attendance
- Average charge per person = 100 / 20 = 5
Therefore, the average charge per person for the entire three days is 5.
1. Calculate the total amount collected each day:
- On the first day: 15 * 2 = 30
- On the second day: 7.50 * 5 = 37.50
- On the third day: 2.50 * 13 = 32.50
2. Calculate the total attendance each day:
- Total attendance for three days = 2 + 5 + 13 = 20
3. Calculate the total amount collected over three days:
- Total amount collected = 30 + 37.50 + 32.50 = 100
4. Calculate the average charge per person for the entire three days:
- Average charge per person = Total amount collected / Total attendance
- Average charge per person = 100 / 20 = 5
Therefore, the average charge per person for the entire three days is 5.
What is the average of first 15 odd numbers among the natural numbers? (SSC MTS 2018)- a)18
- b)15
- c)16
- d)17
Correct answer is option 'B'. Can you explain this answer?
What is the average of first 15 odd numbers among the natural numbers? (SSC MTS 2018)
a)
18
b)
15
c)
16
d)
17
|
|
Ssc Cgl answered |
Here the first 15 odd natural number are
1 , 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23,25, 27, 29
Sum of first 15 odd numbers are 1 + 3 + 5 ....... + 29 = 225
Hence the average is = 225/15 = 15
1 , 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23,25, 27, 29
Sum of first 15 odd numbers are 1 + 3 + 5 ....... + 29 = 225
Hence the average is = 225/15 = 15
What is the arithmetic mean of first 20 odd natural numbers? (SSC CGL 1st Sit. 2015)- a)17
- b)19
- c)22
- d)20
Correct answer is option 'D'. Can you explain this answer?
What is the arithmetic mean of first 20 odd natural numbers? (SSC CGL 1st Sit. 2015)
a)
17
b)
19
c)
22
d)
20
|
Ishaan Roy answered |
Understanding Odd Natural Numbers
The first 20 odd natural numbers are a sequence starting from 1 and increasing by 2 each time. They are:
- 1, 3, 5, 7, 9, 11, 13, 15, 17, 19,
- 21, 23, 25, 27, 29, 31, 33, 35, 37, 39
Finding the Sum of the Numbers
To calculate the arithmetic mean, we first need the sum of these numbers. The sum of the first n odd natural numbers is given by the formula:
- Sum = n^2
For n = 20 (the count of the first 20 odd natural numbers):
- Sum = 20^2 = 400
Calculating the Arithmetic Mean
The arithmetic mean (average) is calculated by dividing the sum by the number of terms:
- Mean = Sum / Number of Terms
- Mean = 400 / 20 = 20
Conclusion
Thus, the arithmetic mean of the first 20 odd natural numbers is:
- 20
The correct answer is option 'D'.
The first 20 odd natural numbers are a sequence starting from 1 and increasing by 2 each time. They are:
- 1, 3, 5, 7, 9, 11, 13, 15, 17, 19,
- 21, 23, 25, 27, 29, 31, 33, 35, 37, 39
Finding the Sum of the Numbers
To calculate the arithmetic mean, we first need the sum of these numbers. The sum of the first n odd natural numbers is given by the formula:
- Sum = n^2
For n = 20 (the count of the first 20 odd natural numbers):
- Sum = 20^2 = 400
Calculating the Arithmetic Mean
The arithmetic mean (average) is calculated by dividing the sum by the number of terms:
- Mean = Sum / Number of Terms
- Mean = 400 / 20 = 20
Conclusion
Thus, the arithmetic mean of the first 20 odd natural numbers is:
- 20
The correct answer is option 'D'.
The present age of a Manoj is twice the sum of the ages of his two children. After 20 years, the age of Manoj will become equal to the sum of the ages of his two children. What is the present age of Manoj? (SSC MTS 2018)- a)40 years
- b)30 years
- c)36 years
- d)35 years
Correct answer is option 'A'. Can you explain this answer?
The present age of a Manoj is twice the sum of the ages of his two children. After 20 years, the age of Manoj will become equal to the sum of the ages of his two children. What is the present age of Manoj? (SSC MTS 2018)
a)
40 years
b)
30 years
c)
36 years
d)
35 years
|
|
Ssc Cgl answered |
Let present age of Manoj is x years.
and their two sons present age are y and z years.
According to the question,
x = 2(y + z) ...(i)
Their ages after 20 years.
x + 20 = (y + 20) + (z + 20)
x = y + z + 20
From equation (1),
x = (x/2) + 20
x - (x/2) = 20
x/2 = 20
⇒ x = 40
Hence, present age of father = 40 years.
and their two sons present age are y and z years.
According to the question,
x = 2(y + z) ...(i)
Their ages after 20 years.
x + 20 = (y + 20) + (z + 20)
x = y + z + 20
From equation (1),
x = (x/2) + 20
x - (x/2) = 20
x/2 = 20
⇒ x = 40
Hence, present age of father = 40 years.
What is the Arithmetic mean of the first 'n' natural numbers? (SSC CGL 1st Sit. 2015)- a)(n+1)/2
- b)
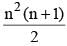
- c)2 (n + 1)
- d)
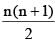
Correct answer is option 'A'. Can you explain this answer?
What is the Arithmetic mean of the first 'n' natural numbers? (SSC CGL 1st Sit. 2015)
a)
(n+1)/2
b)
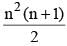
c)
2 (n + 1)
d)
|
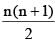
Kiran Reddy answered |
Arithmetic mean of first ‘n’ natural number
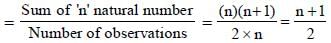
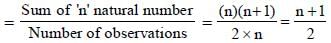
Chapter doubts & questions for Average - SSC CGL Previous Year Papers 2025 is part of SSC CGL exam preparation. The chapters have been prepared according to the SSC CGL exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for SSC CGL 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Average - SSC CGL Previous Year Papers in English & Hindi are available as part of SSC CGL exam.
Download more important topics, notes, lectures and mock test series for SSC CGL Exam by signing up for free.
SSC CGL Previous Year Papers
319 docs|337 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup