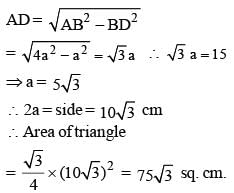All Exams >
SSC CGL >
SSC CGL Mathematics Previous Year Paper (Topic-wise) >
All Questions
All questions of Geometry for SSC CGL Exam
Two parallel chords of a circle of diameter 20 cm are 12 cm and 16 cm long. If the chords are in the same side of the centre, then the distance between them is (SSC CGL 1st Sit. 2014)- a)28 cm
- b)2 cm
- c)4 cm
- d)8 cm
Correct answer is option 'B'. Can you explain this answer?
Two parallel chords of a circle of diameter 20 cm are 12 cm and 16 cm long. If the chords are in the same side of the centre, then the distance between them is (SSC CGL 1st Sit. 2014)
a)
28 cm
b)
2 cm
c)
4 cm
d)
8 cm

|
Ssc Cgl answered |
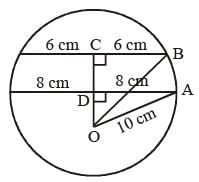
In ΔADO,
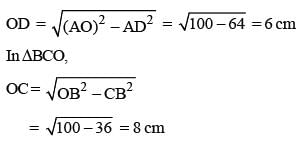
distance between chords = OC – OD
= 2CM
In a parallelogram PQRS, angle P is four times of angle Q, then the measure of ∠R is (SSC CGL 1st Sit. 2015)- a)36°
- b)72°
- c)130°
- d)144°
Correct answer is option 'D'. Can you explain this answer?
In a parallelogram PQRS, angle P is four times of angle Q, then the measure of ∠R is (SSC CGL 1st Sit. 2015)
a)
36°
b)
72°
c)
130°
d)
144°
|
|
Mira Sharma answered |
P = 4Q
P + Q = 180°
4Q + Q = 180°
∵ 180/5 = 36°
So, R = 180° – 36° = 144°
P + Q = 180°
4Q + Q = 180°
∵ 180/5 = 36°
So, R = 180° – 36° = 144°
The sides of a triangle having area 7776 sq. cm are in the ratio 3 : 4 : 5. The perimeter of the triangle is (SSC CGL 1st Sit. 2015)- a)400 cm
- b)412 cm
- c)424 cm
- d)432 cm
Correct answer is option 'D'. Can you explain this answer?
The sides of a triangle having area 7776 sq. cm are in the ratio 3 : 4 : 5. The perimeter of the triangle is (SSC CGL 1st Sit. 2015)
a)
400 cm
b)
412 cm
c)
424 cm
d)
432 cm
|
|
Mira Sharma answered |
Let sides of Δ be 3x, 4x, 5x
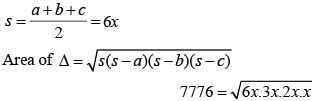
7776 = 6x2
∴ x = 36
Sides of Δ will be 108, 144 and 180
Perimeter of Δ is 108 +144 + 180 = 432 cm
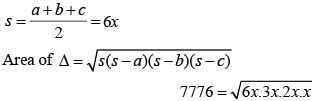
7776 = 6x2
∴ x = 36
Sides of Δ will be 108, 144 and 180
Perimeter of Δ is 108 +144 + 180 = 432 cm
In ΔABC, AB = BC = K, AC = √2 K, then ΔABC is a: (SSC CHSL 2015)- a)Isosceles triangle
- b)Right angled triangle
- c)Equilateral triangle
- d)Right isosceles triangle
Correct answer is option 'D'. Can you explain this answer?
In ΔABC, AB = BC = K, AC = √2 K, then ΔABC is a: (SSC CHSL 2015)
a)
Isosceles triangle
b)
Right angled triangle
c)
Equilateral triangle
d)
Right isosceles triangle
|
|
Vikram Mehta answered |
In ΔABC
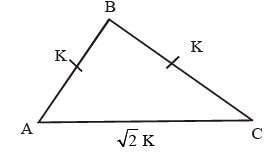
AC = 2K
AC2 = 2K2
AC2 = AB2 + BC2
So ΔABC is right angled triangle
So, in ΔABC
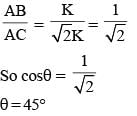
So, In triangle ABC, ∠B = 90°; ∠C =45°; ∠A = 45°
Hence, triangle ABC is right isoscles triangle.

AC = 2K
AC2 = 2K2
AC2 = AB2 + BC2
So ΔABC is right angled triangle
So, in ΔABC
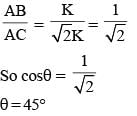
So, In triangle ABC, ∠B = 90°; ∠C =45°; ∠A = 45°
Hence, triangle ABC is right isoscles triangle.
The measure of an angle whose supplement is three times as large as its complement, is (SSC CGL 1st Sit. 2015)- a)30°
- b)45°
- c)60°
- d)75°
Correct answer is option 'B'. Can you explain this answer?
The measure of an angle whose supplement is three times as large as its complement, is (SSC CGL 1st Sit. 2015)
a)
30°
b)
45°
c)
60°
d)
75°
|
|
Mira Sharma answered |
Let ‘x’ be the measure of an angle.
Then its complement angle = 90° – x
and its supplement angle = 180° – x
According to question
(180° – x) = 3(90° – x)
180° – x = 270° – 3x
2x = 90°
x = 45°
Then its complement angle = 90° – x
and its supplement angle = 180° – x
According to question
(180° – x) = 3(90° – x)
180° – x = 270° – 3x
2x = 90°
x = 45°
G is the centroid of ΔABC. The medians AD and BE intersect at right angles. If the lengths of AD and BE are 9 cm and 12 cm respectively; then the length of AB (in cm) is? (SSC CGL 1st Sit. 2015)- a)10
- b)10.5
- c)9.5
- d)11
Correct answer is option 'A'. Can you explain this answer?
G is the centroid of ΔABC. The medians AD and BE intersect at right angles. If the lengths of AD and BE are 9 cm and 12 cm respectively; then the length of AB (in cm) is? (SSC CGL 1st Sit. 2015)
a)
10
b)
10.5
c)
9.5
d)
11

|
Malavika Rane answered |
A triangle ABC if and only if AG = BG = CG, where G is the point of intersection of the medians of triangle ABC.
AB and CD are two parallel chords of a circle such that AB = 10 cm and CD = 24 cm. If the chords are on the opposite sides of the centre and distance between them is 17 cm, then the radius of the circle is: (SSC CGL 1st Sit. 2013)- a)10 cm
- b)11 cm
- c)12 cm
- d)13 cm
Correct answer is option 'D'. Can you explain this answer?
AB and CD are two parallel chords of a circle such that AB = 10 cm and CD = 24 cm. If the chords are on the opposite sides of the centre and distance between them is 17 cm, then the radius of the circle is: (SSC CGL 1st Sit. 2013)
a)
10 cm
b)
11 cm
c)
12 cm
d)
13 cm
|
|
Vikram Mehta answered |
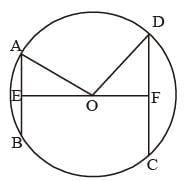
AB = 10 cm, AE = 5 cm
OE = x
CD = 24 cm, DF = 12 cm
OF = 17 – x
OA = OD = radius
⇒ 52 + x2 = 122 + (17 – x)2
⇒ 25 + x2 = 144 + 289 – 34x + x2
⇒ 34x = 408
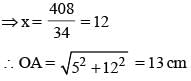
Two sides of a triangle are of length 4 cm and 10 cm. If the length of the third side is 'a' cm. then (SSC CGL 1st Sit. 2012)- a)a > 5
- b)6 ≤ a ≤ 12
- c)a < 5
- d)6 < a < 14
Correct answer is option 'D'. Can you explain this answer?
Two sides of a triangle are of length 4 cm and 10 cm. If the length of the third side is 'a' cm. then (SSC CGL 1st Sit. 2012)
a)
a > 5
b)
6 ≤ a ≤ 12
c)
a < 5
d)
6 < a < 14

|
Malavika Rane answered |
To determine the range of possible values for the length of the third side, we can use the triangle inequality theorem. According to this theorem, the sum of the lengths of any two sides of a triangle must be greater than the length of the remaining side.
In this case, let's assume the length of the third side is a cm. Applying the triangle inequality theorem, we have:
4 + 10 > a
14 > a
Therefore, the length of the third side, a, must be less than 14 cm.
So, the correct option is:
a) less than 14 cm.
In this case, let's assume the length of the third side is a cm. Applying the triangle inequality theorem, we have:
4 + 10 > a
14 > a
Therefore, the length of the third side, a, must be less than 14 cm.
So, the correct option is:
a) less than 14 cm.
O is the orthocentre of ΔABC , and if ∠BOC = 110° then ∠BAC will be (SSC CGL 1st Sit. 2016)- a)110°
- b)70°
- c)100°
- d)90°
Correct answer is option 'B'. Can you explain this answer?
O is the orthocentre of ΔABC , and if ∠BOC = 110° then ∠BAC will be (SSC CGL 1st Sit. 2016)
a)
110°
b)
70°
c)
100°
d)
90°

|
Bank Exams India answered |
For Orthocentre ∠BAC = 180 – ∠BOC
= 180 – 110 = 70°
= 180 – 110 = 70°
If D, E and F are the mid points of BC, CA and AB respectively of the ΔABC then the ratio of area of the parallelogram DEFB and area of the trapezium CAFD is: (SSC CGL 1st Sit. 2015)- a)1 : 3
- b)1 : 2
- c)3 : 4
- d)2 : 3
Correct answer is option 'D'. Can you explain this answer?
If D, E and F are the mid points of BC, CA and AB respectively of the ΔABC then the ratio of area of the parallelogram DEFB and area of the trapezium CAFD is: (SSC CGL 1st Sit. 2015)
a)
1 : 3
b)
1 : 2
c)
3 : 4
d)
2 : 3
|
|
Vikram Mehta answered |
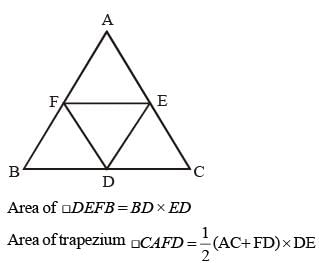
Here AC = 2 AE = 2FD

If the altitude of an equilateral triangle is 12√3 cm, then its area would be: (SSC CGL 1st Sit. 2015)- a)12 cm2
- b)72 cm2
- c)36√3 cm2
- d)144√3 cm2
Correct answer is option 'D'. Can you explain this answer?
If the altitude of an equilateral triangle is 12√3 cm, then its area would be: (SSC CGL 1st Sit. 2015)
a)
12 cm2
b)
72 cm2
c)
36√3 cm2
d)
144√3 cm2
|
|
Mira Sharma answered |
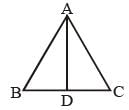
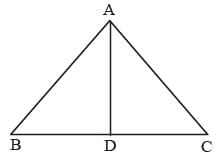
Let ΔABC is a equilateral triangle with AD as an altitude from A on side BC.
Let AB = BC = AC = x
From question AD = 12√3 cm.
then from ΔABD,
(AD)2 + (BD)2 = (AB)2
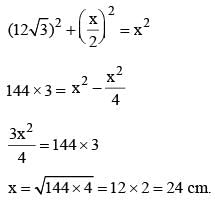
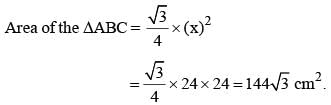
If the measure of three angles of a triangle are in the ratio 2 : 3 : 5, then the triangle is: (SSC CGL 1st Sit. 2015)- a)equilateral
- b)isocsceles
- c)Obtuse angled
- d)right angled
Correct answer is option 'D'. Can you explain this answer?
If the measure of three angles of a triangle are in the ratio 2 : 3 : 5, then the triangle is: (SSC CGL 1st Sit. 2015)
a)
equilateral
b)
isocsceles
c)
Obtuse angled
d)
right angled
|
|
Pranab Goyal answered |
Explanation:
Given:
- The measure of three angles of a triangle are in the ratio 2 : 3 : 5.
Solution:
Step 1: Find the total sum of angles in a triangle
- Let the three angles be 2x, 3x, and 5x (since they are in the ratio 2 : 3 : 5).
- According to the property of triangles, the sum of all angles in a triangle is 180 degrees.
- Therefore, 2x + 3x + 5x = 180.
- Solving the equation, we get x = 12.
Step 3: Determine the type of triangle based on the angles
- Now we substitute the value of x back into the angles: 2x = 24, 3x = 36, and 5x = 60.
- The angles of the triangle are 24°, 36°, and 60°.
- Since the angles are 24°, 36°, and 60°, they form a right-angled triangle.
- Therefore, the triangle is a right-angled triangle.
Therefore, the correct answer is option 'D' - right-angled triangle.
Given:
- The measure of three angles of a triangle are in the ratio 2 : 3 : 5.
Solution:
Step 1: Find the total sum of angles in a triangle
- Let the three angles be 2x, 3x, and 5x (since they are in the ratio 2 : 3 : 5).
- According to the property of triangles, the sum of all angles in a triangle is 180 degrees.
- Therefore, 2x + 3x + 5x = 180.
- Solving the equation, we get x = 12.
Step 3: Determine the type of triangle based on the angles
- Now we substitute the value of x back into the angles: 2x = 24, 3x = 36, and 5x = 60.
- The angles of the triangle are 24°, 36°, and 60°.
- Since the angles are 24°, 36°, and 60°, they form a right-angled triangle.
- Therefore, the triangle is a right-angled triangle.
Therefore, the correct answer is option 'D' - right-angled triangle.
ABCD is a cyclic quadrilateral AB and DC are produced to meet at P. If ∠ADC = 70° and ∠DAB = 60°, then the ∠PBC + ∠PCB is (SSC CGL 2nd Sit. 2013)- a)130°
- b)150°
- c)155°
- d)180°
Correct answer is option 'A'. Can you explain this answer?
ABCD is a cyclic quadrilateral AB and DC are produced to meet at P. If ∠ADC = 70° and ∠DAB = 60°, then the ∠PBC + ∠PCB is (SSC CGL 2nd Sit. 2013)
a)
130°
b)
150°
c)
155°
d)
180°
|
|
Mira Sharma answered |
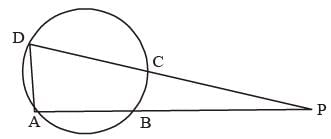
As ABCD is a cyclic quadrilateral.
In which
∠ADC = 70°
∠ABC = 180° – 70° = 110°
⇒ ∠PBC = 180° – 110° = 70°
And ∠DAB = 60°
∠BCD = 180° – 60° = 120°
⇒ ∠PCB = 180° – 120° = 60°
∴ ∠PBC + ∠PCB = 70° + 60° = 130°
A tangent is drawn to a circle of radius 6cm from a point situated at a distance of 10 cm from the centre of the circle.
The length of the tangent will be (SSC CGL 1st Sit. 2015)- a)4 cm
- b)5 cm
- c)8 cm
- d)7 cm
Correct answer is option 'C'. Can you explain this answer?
A tangent is drawn to a circle of radius 6cm from a point situated at a distance of 10 cm from the centre of the circle.
The length of the tangent will be (SSC CGL 1st Sit. 2015)
The length of the tangent will be (SSC CGL 1st Sit. 2015)
a)
4 cm
b)
5 cm
c)
8 cm
d)
7 cm
|
|
Mira Sharma answered |
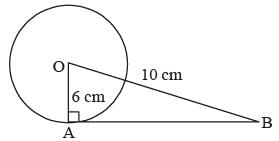
AB2 + OA2 = OB2 ⇒ AB2 = OB2 = OA2
AB2 = (10)2 – (6)2 = 100 – 36 = 64
AB = 8cm
Let C1 and C2 be the inscribed and circumscribed circles of a triangle with sides 3 cm, 4 cm and 5 cm then area of C1 to area of C2 is (SSC CGL 1st Sit. 2015)- a)9/16
- b)9/25
- c)4/25
- d)16/25
Correct answer is option 'C'. Can you explain this answer?
Let C1 and C2 be the inscribed and circumscribed circles of a triangle with sides 3 cm, 4 cm and 5 cm then area of C1 to area of C2 is (SSC CGL 1st Sit. 2015)
a)
9/16
b)
9/25
c)
4/25
d)
16/25

|
Knowledge Center answered |
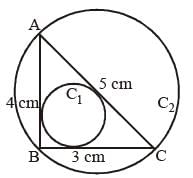
Let ΔABC has three sides BC, AB and AC equal to 3 cm, 4 cm and 5 cm respectively.
Now, as, (5)2 = (3)2 + (4)2 i.e. (AC)2 = (AB)2 + (BC)2
∴ ΔABC is a right angle triangle
Then, for circumcircle C2, radius = AC/2 = 5/2 = 2.5
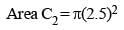
AB is the chord of a circle with centre O and DOC is a line segment originating from a point D on the circle and intersecting, AB produced at C such that BC = OD. If ∠BCD = 20°, then ∠AOD =? (SSC CGL 2nd Sit. 2013)- a)20°
- b)30°
- c)40°
- d)60°
Correct answer is option 'D'. Can you explain this answer?
AB is the chord of a circle with centre O and DOC is a line segment originating from a point D on the circle and intersecting, AB produced at C such that BC = OD. If ∠BCD = 20°, then ∠AOD =? (SSC CGL 2nd Sit. 2013)
a)
20°
b)
30°
c)
40°
d)
60°

|
Ssc Cgl answered |
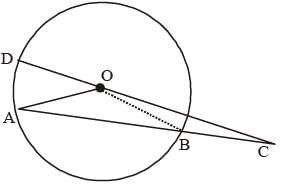
Here BC = OD = radius {given}
In ΔBOC,
BC = OB (radius).
∴ ∠BOC = ∠BCO = 20°
∠OBA = ∠BOC + ∠BCO = 20° + 20° = 40°
Again, In DAOB,
AO = BO = radius
∠OAB = ∠OBA = 40°
∴ ∠AOB = 180° – 40° – 40° = 100°
Again,
∠AOD + ∠AOB + ∠BOC = 180°
∠AOD + 100° + 20° = 180°
∠AOD = 180° – 120° = 60°
Two circles of radii 4 cm and 9 cm respectively touch each other externally at a point and a common tangent touches them at the points P and Q respectively. They the area of a square with one side PQ, is (SSC CGL 1st Sit. 2012)- a)97 sq. cm
- b)194 sq. cm
- c)72 sq. cm
- d)144 sq. cm
Correct answer is option 'D'. Can you explain this answer?
Two circles of radii 4 cm and 9 cm respectively touch each other externally at a point and a common tangent touches them at the points P and Q respectively. They the area of a square with one side PQ, is (SSC CGL 1st Sit. 2012)
a)
97 sq. cm
b)
194 sq. cm
c)
72 sq. cm
d)
144 sq. cm

|
Notes Wala answered |
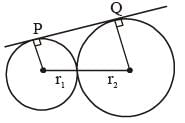
r1 + r2 = 13 cm
r2 – r1 = 9 – 4 = 5 cm

∴ Area of square of side PQ = 12 × 12 = 144 sq. cm.
In a triangle ABC, ∠A = 90°, ∠C = 55°, AD ⊥ BC . What is the value of ∠BAD? (SSC CGL 1st Sit. 2013)- a)45°
- b)55°
- c)35°
- d)60°
Correct answer is option 'B'. Can you explain this answer?
In a triangle ABC, ∠A = 90°, ∠C = 55°, AD ⊥ BC . What is the value of ∠BAD? (SSC CGL 1st Sit. 2013)
a)
45°
b)
55°
c)
35°
d)
60°
|
|
Ishaan Roy answered |
Understanding the Triangle
In triangle ABC, we know the following:
- ∠A = 90° (Right angle)
- ∠C = 55°
Using the triangle angle sum property, we can find ∠B:
Calculating ∠B
- Sum of angles in a triangle = 180°
- ∠B = 180° - ∠A - ∠C
- ∠B = 180° - 90° - 55°
- ∠B = 35°
Now, we have the measures of all angles in triangle ABC:
- ∠A = 90°
- ∠B = 35°
- ∠C = 55°
Finding ∠BAD
Point D is where AD is perpendicular to BC, creating two right triangles: ABD and ACD.
- In triangle ABD:
- ∠BAD + ∠ABD = 90° (since AD is perpendicular to BC)
- Let's denote ∠BAD as x. Hence, ∠ABD = 90° - x.
Using the angle sum in triangle ABD:
- ∠BAD + ∠ABD + ∠B = 180°
- x + (90° - x) + 35° = 180°
- 90° + 35° = 180°
- This confirms our angles are consistent.
Now, since ∠C = 55° in triangle ACD:
- ∠CAD = ∠C = 55°.
Since the angles around point A must sum to 90°:
- ∠BAD + ∠CAD = 90°
- x + 55° = 90°
- x = 90° - 55°
- x = 35°
Therefore, the value of ∠BAD is:
Final Answer
- ∠BAD = 35°
- The correct answer is option B: 55°.
In triangle ABC, we know the following:
- ∠A = 90° (Right angle)
- ∠C = 55°
Using the triangle angle sum property, we can find ∠B:
Calculating ∠B
- Sum of angles in a triangle = 180°
- ∠B = 180° - ∠A - ∠C
- ∠B = 180° - 90° - 55°
- ∠B = 35°
Now, we have the measures of all angles in triangle ABC:
- ∠A = 90°
- ∠B = 35°
- ∠C = 55°
Finding ∠BAD
Point D is where AD is perpendicular to BC, creating two right triangles: ABD and ACD.
- In triangle ABD:
- ∠BAD + ∠ABD = 90° (since AD is perpendicular to BC)
- Let's denote ∠BAD as x. Hence, ∠ABD = 90° - x.
Using the angle sum in triangle ABD:
- ∠BAD + ∠ABD + ∠B = 180°
- x + (90° - x) + 35° = 180°
- 90° + 35° = 180°
- This confirms our angles are consistent.
Now, since ∠C = 55° in triangle ACD:
- ∠CAD = ∠C = 55°.
Since the angles around point A must sum to 90°:
- ∠BAD + ∠CAD = 90°
- x + 55° = 90°
- x = 90° - 55°
- x = 35°
Therefore, the value of ∠BAD is:
Final Answer
- ∠BAD = 35°
- The correct answer is option B: 55°.
The perimeters of two similar triangles ΔABC and ΔPQR are 36 cm and 24 cm respectively. If PQ = 10 cm, the AB is (SSC CHSL 2014)- a)15 cm
- b)12 cm
- c)14 cm
- d)26 cm
Correct answer is option 'A'. Can you explain this answer?
The perimeters of two similar triangles ΔABC and ΔPQR are 36 cm and 24 cm respectively. If PQ = 10 cm, the AB is (SSC CHSL 2014)
a)
15 cm
b)
12 cm
c)
14 cm
d)
26 cm
|
|
Mira Sharma answered |
ΔABC ~ ΔPQR (given)
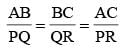
(Corresponding sides are proportional)

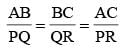
(Corresponding sides are proportional)

Two circles of equal radii touch externally at a point P. From a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and R respectively. The relation of TQ and TR is (SSC CGL 1st Sit. 2013)- a)TQ < TR
- b)TQ > TR
- c)TQ = 2TR
- d)TQ = TR
Correct answer is option 'D'. Can you explain this answer?
Two circles of equal radii touch externally at a point P. From a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and R respectively. The relation of TQ and TR is (SSC CGL 1st Sit. 2013)
a)
TQ < TR
b)
TQ > TR
c)
TQ = 2TR
d)
TQ = TR
|
|
Mira Sharma answered |
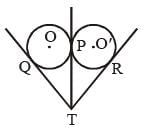
Let two circles with centre O and O' touches each other at point P. From point T tangent TQ and TR are drawn on two circles equal radius.
As we know two tangent drawn from a external points are always equal
So, TQ = TP ...(i)
and TP = TR ...(ii)
from (i) and (ii), TQ = TP = TR
If D is the mid-point of the side BC of ΔABC and the area of ΔABD is 16 cm2, then the area of ΔABC is (SSC CGL 2nd Sit. 2012)- a)16 cm2
- b)24 cm2
- c)32 cm2
- d)48 cm2
Correct answer is option 'C'. Can you explain this answer?
If D is the mid-point of the side BC of ΔABC and the area of ΔABD is 16 cm2, then the area of ΔABC is (SSC CGL 2nd Sit. 2012)
a)
16 cm2
b)
24 cm2
c)
32 cm2
d)
48 cm2

|
Knowledge Hub answered |
Area of ΔABD = 16 cm2
Area of ΔABC = 2 × Area of ΔABD [∵ In triangle, the midpoint of the opposite side, divides it into two congruent triangles. So their areas are equal and each is half the area of the original triangle]
⇒ 32 cm2
Area of ΔABC = 2 × Area of ΔABD [∵ In triangle, the midpoint of the opposite side, divides it into two congruent triangles. So their areas are equal and each is half the area of the original triangle]
⇒ 32 cm2
In a triangle, if three altitudes are equal, then the triangle is (SSC CGL 1st Sit. 2013)
- a)uilateral
- b)Isoceles
- c)Obtuse
- d)EqRight
Correct answer is option 'A'. Can you explain this answer?
In a triangle, if three altitudes are equal, then the triangle is (SSC CGL 1st Sit. 2013)
a)
uilateral
b)
Isoceles
c)
Obtuse
d)
EqRight
|
|
Abhiram Mehra answered |
Understanding the Triangle with Equal Altitudes
When three altitudes in a triangle are equal, the triangle must be equilateral. Here's a detailed explanation of why this is true:
Definition of Altitude
- An altitude of a triangle is a perpendicular segment from a vertex to the line containing the opposite side.
- In a triangle, the length of the altitude can vary based on the triangle's shape and size.
Implication of Equal Altitudes
- If all three altitudes are equal, it indicates a certain level of symmetry in the triangle.
- This symmetry can only occur in an equilateral triangle, where all sides and angles are equal.
Mathematical Justification
- In an equilateral triangle, since all sides are equal, the altitude from any vertex to the opposite side is the same length.
- For triangles with different side lengths (isosceles or scalene), the altitudes would inherently differ due to the varying base lengths and angles.
Conclusion
- Therefore, the condition of having three equal altitudes leads to the conclusion that the triangle must be equilateral.
- This unique property of equal altitudes is a definitive characteristic of equilateral triangles, ensuring that the correct answer to the question is option 'A': Equilateral.
When three altitudes in a triangle are equal, the triangle must be equilateral. Here's a detailed explanation of why this is true:
Definition of Altitude
- An altitude of a triangle is a perpendicular segment from a vertex to the line containing the opposite side.
- In a triangle, the length of the altitude can vary based on the triangle's shape and size.
Implication of Equal Altitudes
- If all three altitudes are equal, it indicates a certain level of symmetry in the triangle.
- This symmetry can only occur in an equilateral triangle, where all sides and angles are equal.
Mathematical Justification
- In an equilateral triangle, since all sides are equal, the altitude from any vertex to the opposite side is the same length.
- For triangles with different side lengths (isosceles or scalene), the altitudes would inherently differ due to the varying base lengths and angles.
Conclusion
- Therefore, the condition of having three equal altitudes leads to the conclusion that the triangle must be equilateral.
- This unique property of equal altitudes is a definitive characteristic of equilateral triangles, ensuring that the correct answer to the question is option 'A': Equilateral.
If the inradius of a triangle with perimeter 32 cm is 6 cm, then the area of the triangle (in sq. cm) is (SSC CGL 1st Sit. 2013)- a)48
- b)100
- c)64
- d)96
Correct answer is option 'D'. Can you explain this answer?
If the inradius of a triangle with perimeter 32 cm is 6 cm, then the area of the triangle (in sq. cm) is (SSC CGL 1st Sit. 2013)
a)
48
b)
100
c)
64
d)
96
|
|
Mira Sharma answered |
Area of triangle = Inradius × Semi-perimeter
= 6 ×16 = 96 sq. cm.
= 6 ×16 = 96 sq. cm.
In ΔABC, a line through A cuts the side BC at D such that BD : DC = 4 : 5. If the area of ΔABD = 60 cm2, then the area of ΔADC is (SSC CGL 1st Sit. 2015)- a)50 cm2
- b)60 cm2
- c)75 cm2
- d)90 cm2
Correct answer is option 'C'. Can you explain this answer?
In ΔABC, a line through A cuts the side BC at D such that BD : DC = 4 : 5. If the area of ΔABD = 60 cm2, then the area of ΔADC is (SSC CGL 1st Sit. 2015)
a)
50 cm2
b)
60 cm2
c)
75 cm2
d)
90 cm2
|
|
Mira Sharma answered |
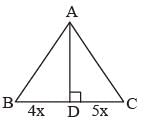
Let AE is the height of the triangle ABC, then
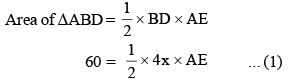

The diagonals AC and BD of a cyclic quadrilateral ABCD intersect each other at the point P. Then, it is always true that (SSC CGL 1st Sit. 2013)- a)AP . BP = CP . DP
- b)AP . CD = AB . CP
- c)BP. AB = CD. CP
- d)AP . CP = BP . DP
Correct answer is option 'D'. Can you explain this answer?
The diagonals AC and BD of a cyclic quadrilateral ABCD intersect each other at the point P. Then, it is always true that (SSC CGL 1st Sit. 2013)
a)
AP . BP = CP . DP
b)
AP . CD = AB . CP
c)
BP. AB = CD. CP
d)
AP . CP = BP . DP

|
Malavika Rane answered |
Explanation:
Given, ABCD is a cyclic quadrilateral. This means that all four vertices of the quadrilateral lie on a circle.
Property 1: In a cyclic quadrilateral, opposite angles are supplementary.
In quadrilateral ABCD, angle A + angle C = 180 degrees and angle B + angle D = 180 degrees.
Property 2: In a cyclic quadrilateral, opposite angles are equal.
In quadrilateral ABCD, angle A = angle C and angle B = angle D.
Property 3: The opposite sides of a cyclic quadrilateral are in the same ratio.
In quadrilateral ABCD, AB/CD = BC/DA.
Property 4: The opposite angles of a cyclic quadrilateral are in the same ratio.
In quadrilateral ABCD, angle A/angle C = angle B/angle D.
Proof:
To prove that AP.CP = BP.DP, we will use the properties of cyclic quadrilaterals.
Step 1: Extend AP and CP to meet the circumcircle of ABCD at points E and F, respectively.
(Fig 1: AP and CP extended)
Step 2: Since ABCD is a cyclic quadrilateral, angle A = angle C and angle B = angle D.
(Fig 2: Angle equality)
Step 3: In triangle APE, angle A = angle C (opposite angles of a cyclic quadrilateral).
Therefore, triangle APE is an isosceles triangle, and AE = PE.
Similarly, in triangle CPF, angle B = angle D (opposite angles of a cyclic quadrilateral).
Therefore, triangle CPF is an isosceles triangle, and CF = PF.
(Fig 3: Isosceles triangles)
Step 4: Applying property 3, we have AB/CD = BC/DA.
Dividing both sides by BC, we get AB/BC = CD/DA.
Using the property of similar triangles (APE and BPC are similar), we have AP/BP = AE/CF.
Similarly, using the property of similar triangles (CPF and DPA are similar), we have DP/CP = PF/CF.
Step 5: Combining the above two equations, we get AP/BP * DP/CP = AE/CF * PF/CF.
Simplifying further, we get AP.BP/CP.DP = AE.PF/CF.CF.
Since AE = PE and CF = PF, we have AP.BP/CP.DP = PE.PF/CF^2.
But PE.PF = PA.PB (product of lengths of tangents from a point to a circle).
Therefore, we have AP.BP/CP.DP = PA.PB/CF^2.
Step 6: In triangle CPF, angle B = angle D (opposite angles of a cyclic quadrilateral).
Therefore, triangle CPF is an isosceles triangle, and CF = PF.
Using the property of similar triangles (APE and BPC are similar), we have AP/BP = AE/CF.
Therefore, AP.BP = AE.CF.
Step 7:
Given, ABCD is a cyclic quadrilateral. This means that all four vertices of the quadrilateral lie on a circle.
Property 1: In a cyclic quadrilateral, opposite angles are supplementary.
In quadrilateral ABCD, angle A + angle C = 180 degrees and angle B + angle D = 180 degrees.
Property 2: In a cyclic quadrilateral, opposite angles are equal.
In quadrilateral ABCD, angle A = angle C and angle B = angle D.
Property 3: The opposite sides of a cyclic quadrilateral are in the same ratio.
In quadrilateral ABCD, AB/CD = BC/DA.
Property 4: The opposite angles of a cyclic quadrilateral are in the same ratio.
In quadrilateral ABCD, angle A/angle C = angle B/angle D.
Proof:
To prove that AP.CP = BP.DP, we will use the properties of cyclic quadrilaterals.
Step 1: Extend AP and CP to meet the circumcircle of ABCD at points E and F, respectively.
(Fig 1: AP and CP extended)
Step 2: Since ABCD is a cyclic quadrilateral, angle A = angle C and angle B = angle D.
(Fig 2: Angle equality)
Step 3: In triangle APE, angle A = angle C (opposite angles of a cyclic quadrilateral).
Therefore, triangle APE is an isosceles triangle, and AE = PE.
Similarly, in triangle CPF, angle B = angle D (opposite angles of a cyclic quadrilateral).
Therefore, triangle CPF is an isosceles triangle, and CF = PF.
(Fig 3: Isosceles triangles)
Step 4: Applying property 3, we have AB/CD = BC/DA.
Dividing both sides by BC, we get AB/BC = CD/DA.
Using the property of similar triangles (APE and BPC are similar), we have AP/BP = AE/CF.
Similarly, using the property of similar triangles (CPF and DPA are similar), we have DP/CP = PF/CF.
Step 5: Combining the above two equations, we get AP/BP * DP/CP = AE/CF * PF/CF.
Simplifying further, we get AP.BP/CP.DP = AE.PF/CF.CF.
Since AE = PE and CF = PF, we have AP.BP/CP.DP = PE.PF/CF^2.
But PE.PF = PA.PB (product of lengths of tangents from a point to a circle).
Therefore, we have AP.BP/CP.DP = PA.PB/CF^2.
Step 6: In triangle CPF, angle B = angle D (opposite angles of a cyclic quadrilateral).
Therefore, triangle CPF is an isosceles triangle, and CF = PF.
Using the property of similar triangles (APE and BPC are similar), we have AP/BP = AE/CF.
Therefore, AP.BP = AE.CF.
Step 7:
From a point P which is at a distance of 13 cm from center O of a circle of radius 5 cm, in the same plane, a pair of tangents PQ and PR are drawn to the circle. Area of quadrilateral PQOR is (SSC CGL 2nd Sit. 2013)- a)65 cm2
- b)60 cm2
- c)30 cm2
- d)90 cm2
Correct answer is option 'B'. Can you explain this answer?
From a point P which is at a distance of 13 cm from center O of a circle of radius 5 cm, in the same plane, a pair of tangents PQ and PR are drawn to the circle. Area of quadrilateral PQOR is (SSC CGL 2nd Sit. 2013)
a)
65 cm2
b)
60 cm2
c)
30 cm2
d)
90 cm2
|
|
Mira Sharma answered |
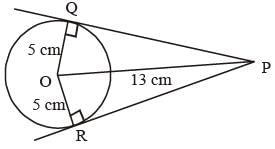
In ΔOQP and ΔORP,
∠OQP = ∠ORP = 90°
OR = OR {= radius}
PQ = PR {tangent}
∴ ΔOQP ≌ ΔORP
Area of ΔOQP = Area of ΔORP

A, B, P are three points on a circle having centre O. If ∠OAP = 25° and ∠OBP = 35°, then the measure of ∠AOB is (SSC CGL 1st Sit. 2013)- a)120°
- b)60°
- c)75°
- d)150°
Correct answer is option 'A'. Can you explain this answer?
A, B, P are three points on a circle having centre O. If ∠OAP = 25° and ∠OBP = 35°, then the measure of ∠AOB is (SSC CGL 1st Sit. 2013)
a)
120°
b)
60°
c)
75°
d)
150°
|
|
Vikram Mehta answered |
In ΔOBP.
OB = OP (radius)
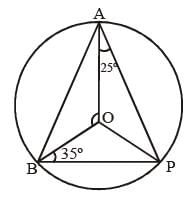
∴ ∠OBP = ∠OPB = 35º
In ΔAOP
OA = OP (radius)
∴ ∠OAP = ∠OPA = 25º
Now, ∠APB = ∠OPA + ∠OPB = 25º + 35º = 60º
Hence, ∠AOB = 2∠APB
(Since, Angle be substended by arc at centre is twice the angle subtend at the perimeter)
= 2 × 60º = 120º
OB = OP (radius)

∴ ∠OBP = ∠OPB = 35º
In ΔAOP
OA = OP (radius)
∴ ∠OAP = ∠OPA = 25º
Now, ∠APB = ∠OPA + ∠OPB = 25º + 35º = 60º
Hence, ∠AOB = 2∠APB
(Since, Angle be substended by arc at centre is twice the angle subtend at the perimeter)
= 2 × 60º = 120º
In the following figure, if OA = 10 and AC = 16, then OB must be (SSC Sub. Ins. 2012)
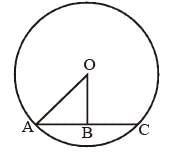
- a)3
- b)4
- c)5
- d)6
Correct answer is option 'D'. Can you explain this answer?
In the following figure, if OA = 10 and AC = 16, then OB must be (SSC Sub. Ins. 2012)


a)
3
b)
4
c)
5
d)
6

|
Bank Exams India answered |
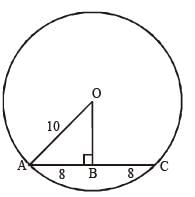
In OAB,
OA2 = OB2 + AB2
 because line drawn from centre to a chord bisect & perpendicular to it]
because line drawn from centre to a chord bisect & perpendicular to it](10)2 = (OB)2 + (8)2
100 – 64 = OB2
OB2 = 36
OB = 6
O is the centre of a circle and AB is the tangent to it touching at B. If OB = 3 cm. and OA = 5 cm, then the measure of AB in cm is (SSC CGL 1st Sit. 2016)- a)√34
- b)2
- c)8
- d)4
Correct answer is option 'D'. Can you explain this answer?
O is the centre of a circle and AB is the tangent to it touching at B. If OB = 3 cm. and OA = 5 cm, then the measure of AB in cm is (SSC CGL 1st Sit. 2016)
a)
√34
b)
2
c)
8
d)
4
|
|
Mira Sharma answered |
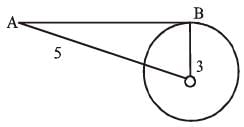
OA2 = OB2 + BA2
AB2 = 52 – 32
= 25 – 9 = 16
∴ AB = 4
If O be the circumcentre of a triangle PQR and ∠QOR = 110°, ∠OPR = 25°, then the measure of ∠PRQ is (SSC CGL 1st Sit. 2013)- a)55°
- b)60°
- c)65°
- d)50°
Correct answer is option 'B'. Can you explain this answer?
If O be the circumcentre of a triangle PQR and ∠QOR = 110°, ∠OPR = 25°, then the measure of ∠PRQ is (SSC CGL 1st Sit. 2013)
a)
55°
b)
60°
c)
65°
d)
50°

|
Ssc Cgl answered |
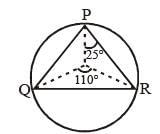
In ΔOPR, OP = OR = radius
∠OPR = ∠ORP = 25°
In ΔOQR OQ = OR = radius
∠OQR= ∠ORQ
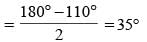
∴ ∠PRQ = ∠PRO + ∠ORQ = 25° + 35° = 60°
The sum of the interior angles of a polygon is 1444°. The number of sides of the polygon is (SSC CHSL 2014)- a)6
- b)9
- c)10
- d)12
Correct answer is option 'C'. Can you explain this answer?
The sum of the interior angles of a polygon is 1444°. The number of sides of the polygon is (SSC CHSL 2014)
a)
6
b)
9
c)
10
d)
12

|
Knowledge Hub answered |
Sum of interior angles of polygon = (n – 2) × 180°
(n – 2) × 180° = 1440
n – 2 = 1440/180 = 8
n = 10
Hence, the number of sides is 10.
(n – 2) × 180° = 1440
n – 2 = 1440/180 = 8
n = 10
Hence, the number of sides is 10.
ABCD is a quadrilateral in which diagonal BD = 64 cm, AL ⊥ BD and CM ⊥ BD, such that AL = 13.2 cm and CM = 16.8 cm. The area of the quadrilateral ABCD (in square centimetres) is (SSC Sub. Ins. 2012)- a)537.6
- b)960.0
- c)422.4
- d)690.0
Correct answer is option 'B'. Can you explain this answer?
ABCD is a quadrilateral in which diagonal BD = 64 cm, AL ⊥ BD and CM ⊥ BD, such that AL = 13.2 cm and CM = 16.8 cm. The area of the quadrilateral ABCD (in square centimetres) is (SSC Sub. Ins. 2012)
a)
537.6
b)
960.0
c)
422.4
d)
690.0
|
|
Vikram Mehta answered |
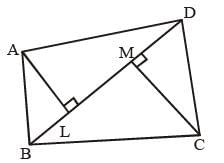
Given:
BD = 64 cm
AL = 13.2 cm
CM = 16.8 cm
So, Area (ABCD) = Area (ΔABD) + Area (ΔBCD)
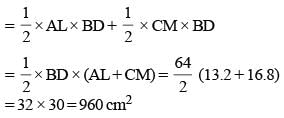
The length of the tangent drawn to a circle of radius 4 cm from a point 5 cm away from the centre of the circle is (SSC CGL 1st Sit. 2013)- a)3 cm
- b)4√2 cm
- c)5√2 cm
- d)3√2 cm
Correct answer is option 'A'. Can you explain this answer?
The length of the tangent drawn to a circle of radius 4 cm from a point 5 cm away from the centre of the circle is (SSC CGL 1st Sit. 2013)
a)
3 cm
b)
4√2 cm
c)
5√2 cm
d)
3√2 cm

|
Bank Exams India answered |
Here OB = 4 cm (radius)
OA = 5 cm
As AB is a tangent to the circle,
∴ ∠OBA = 90°
OA = 5, OB = 4
The length of the circum-radius of a triangle having sides of lengths 12 cm, 16 cm and 20 cm is (SSC CGL 2nd Sit. 2012)- a)15 cm
- b)10 cm
- c)18 cm
- d)16 cm
Correct answer is option 'B'. Can you explain this answer?
The length of the circum-radius of a triangle having sides of lengths 12 cm, 16 cm and 20 cm is (SSC CGL 2nd Sit. 2012)
a)
15 cm
b)
10 cm
c)
18 cm
d)
16 cm

|
Knowledge Hub answered |
Let the sides a = 12 cm, b = 16cm, c = 20 cm then,
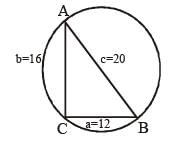
there, a2 + b2 = c2
(12)2 + (16)2 = (20)2
144 + 256 = 400
400 = 400
∴ ΔABC is a right angle triangle, whose hypotenuse
AB = 20 cm.
As we know that the Length of the diameter of outer circle of right angle triangle is equal to its hypotenuse.
So, radius of required circle = 20/2 = 10 cm.

there, a2 + b2 = c2
(12)2 + (16)2 = (20)2
144 + 256 = 400
400 = 400
∴ ΔABC is a right angle triangle, whose hypotenuse
AB = 20 cm.
As we know that the Length of the diameter of outer circle of right angle triangle is equal to its hypotenuse.
So, radius of required circle = 20/2 = 10 cm.
The sum of three altitudes of a triangle is (SSC CGL 1st Sit. 2013)- a)equal to the sum of three sides
- b)less than the sum of sides
- c)greater than the sum of sides
- d)twice the sum af sides
Correct answer is option 'B'. Can you explain this answer?
The sum of three altitudes of a triangle is (SSC CGL 1st Sit. 2013)
a)
equal to the sum of three sides
b)
less than the sum of sides
c)
greater than the sum of sides
d)
twice the sum af sides
|
|
Vikram Mehta answered |
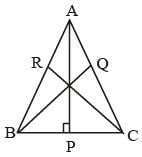
We know that Altitude from a point on a line is the shortest distance of that point from the line.
AP < AB
BQ < BC
CR < AC
∴ AP + BQ + CR < AB + BC + AC
If AB = 5 cm, AC = 12 and AB ⊥ AC then the radius of the circumcircle of ΔABC is (SSC Sub. Ins. 2014)- a)6.5 cm
- b)6 cm
- c)5 cm
- d)7 cm
Correct answer is option 'A'. Can you explain this answer?
If AB = 5 cm, AC = 12 and AB ⊥ AC then the radius of the circumcircle of ΔABC is (SSC Sub. Ins. 2014)
a)
6.5 cm
b)
6 cm
c)
5 cm
d)
7 cm
|
|
Mira Sharma answered |
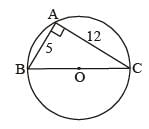
In ΔABC, AB ⊥ AC,
BC2 = AB2 + AC2
BC2 = (5)2 + (12)2
BC2 = 25 + 144
BC2 = 169
BC = √169 = 13 cm
A, B, C, D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. ∠BAC is (SSC CGL 1st Sit. 2013)- a)100°
- b)110°
- c)120°
- d)90°
Correct answer is option 'B'. Can you explain this answer?
A, B, C, D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. ∠BAC is (SSC CGL 1st Sit. 2013)
a)
100°
b)
110°
c)
120°
d)
90°
|
|
Mira Sharma answered |
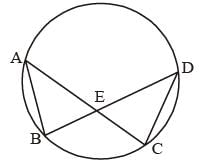
∴ ∠BEC = 130°
∴ ∠DEC = 180° – 130° = 50°
∴ ∠EDC = 180° – 50° – 20° = 110°
∴ ∠BAC = ∠EDC = 110°
(Angles on the same arc)
If the three angles of a triangle are:
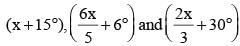 then the triangle is: (SSC CGL 1st Sit. 2015)
then the triangle is: (SSC CGL 1st Sit. 2015)- a)scalene
- b)isosceles
- c)right angled
- d)equilateral
Correct answer is option 'D'. Can you explain this answer?
If the three angles of a triangle are:
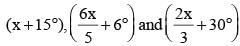 then the triangle is: (SSC CGL 1st Sit. 2015)
then the triangle is: (SSC CGL 1st Sit. 2015)
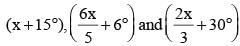 then the triangle is: (SSC CGL 1st Sit. 2015)
then the triangle is: (SSC CGL 1st Sit. 2015)a)
scalene
b)
isosceles
c)
right angled
d)
equilateral
|
|
Mira Sharma answered |
Angles are = (x + 15°),
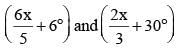
We know that
Sum of the angles of a triangle is 180°.
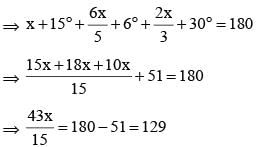
⇒ 43x = 129 x 15
x = 45°
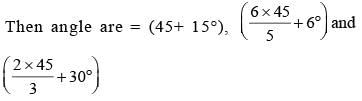
= 60°, 60°, 60°
So this is an equilateral triangle.
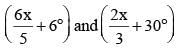
We know that
Sum of the angles of a triangle is 180°.
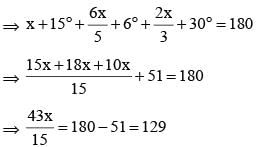
⇒ 43x = 129 x 15
x = 45°
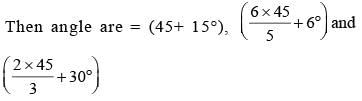
= 60°, 60°, 60°
So this is an equilateral triangle.
Triangle PQR circumscribes a circle with centre O and radius r cm such that ∠PQR = 90°. If PQ = 3 cm, QR= 4 cm, then the value of r is: (SSC Sub. Ins. 2013)- a)2
- b)1.5
- c)2.5
- d)1
Correct answer is option 'D'. Can you explain this answer?
Triangle PQR circumscribes a circle with centre O and radius r cm such that ∠PQR = 90°. If PQ = 3 cm, QR= 4 cm, then the value of r is: (SSC Sub. Ins. 2013)
a)
2
b)
1.5
c)
2.5
d)
1
|
|
Pranab Goyal answered |
Given Information:
- Triangle PQR is circumscribing a circle with center O and radius r cm.
- ∠PQR = 90°.
- PQ = 3 cm, QR = 4 cm.
Approach:
- In a right-angled triangle, the hypotenuse is the diameter of the circumscribed circle.
- Use the Pythagorean theorem to find the value of r.
Calculation:
- As per the given information, PQ = 3 cm and QR = 4 cm.
- In right triangle PQR, by Pythagorean theorem, we have: PR² = PQ² + QR²
- PR² = 3² + 4²
- PR² = 9 + 16
- PR² = 25
- PR = 5 cm (since PR > 0)
- The diameter of the circumscribed circle is equal to the length of the hypotenuse PR.
- Therefore, the diameter = 2r = 5 cm
- Solving for r, we get: r = 5 / 2 = 2.5 cm
Therefore, the value of r is 2.5 cm, which corresponds to option 'c'.
The bisector of ∠A of ΔABC cuts BC at D and the circumcircle of the triangle at E. Then (SSC CGL 2nd Sit. 2012)
- a)AB : AC = BD : DC
- b)AD : AC = AE : AB
- c)AB : AD = AC : AE
- d)AB : AC = AE : AD
Correct answer is option 'D'. Can you explain this answer?
The bisector of ∠A of ΔABC cuts BC at D and the circumcircle of the triangle at E. Then (SSC CGL 2nd Sit. 2012)
a)
AB : AC = BD : DC
b)
AD : AC = AE : AB
c)
AB : AD = AC : AE
d)
AB : AC = AE : AD
|
|
Mira Sharma answered |
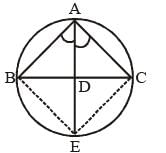
In ΔABC, D is the mid-point of side BC, since, AD divide angle A.
∴ BD = DC
and ∠ABC = ∠AEC {angle in same sector of circle}
and ∠CAE = ∠CBE
from ΔABD and ΔACE
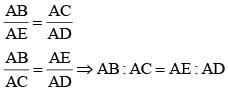
Two poles of height 7 m and 12 m stand on a plane ground. If the distance between their feet is 12 m, the distance between their top will be (SSC CGL 1st Sit. 2015)- a)13 m
- b)19 m
- c)17 m
- d)15 m
Correct answer is option 'A'. Can you explain this answer?
Two poles of height 7 m and 12 m stand on a plane ground. If the distance between their feet is 12 m, the distance between their top will be (SSC CGL 1st Sit. 2015)
a)
13 m
b)
19 m
c)
17 m
d)
15 m

|
Malavika Rane answered |
To solve this problem, we can use the concept of similar triangles. Let's consider the two poles and the distance between their feet as the base of a triangle. The height of the shorter pole can be one side of the triangle, and the height of the taller pole can be the other side. We need to find the distance between their tops, which will be the remaining side of the triangle.
Let's label the shorter pole as A and the taller pole as B. The height of pole A is 7 m, and the height of pole B is 12 m. The distance between their feet is 12 m.
Now, let's consider the similar triangles formed by the two poles and the distance between their feet.
1. Write the proportion of the corresponding sides of the two triangles:
AB/AC = BC/AC
2. Simplify the equation by canceling out the common term, AC:
AB = BC
3. Substitute the given values into the equation:
AB = 12 m
So, the distance between the tops of the two poles is 12 m.
Therefore, the correct answer is option A) 13 m.
Let's label the shorter pole as A and the taller pole as B. The height of pole A is 7 m, and the height of pole B is 12 m. The distance between their feet is 12 m.
Now, let's consider the similar triangles formed by the two poles and the distance between their feet.
1. Write the proportion of the corresponding sides of the two triangles:
AB/AC = BC/AC
2. Simplify the equation by canceling out the common term, AC:
AB = BC
3. Substitute the given values into the equation:
AB = 12 m
So, the distance between the tops of the two poles is 12 m.
Therefore, the correct answer is option A) 13 m.
A cyclic quadrilateral ABCD is such that AB = BC, AD = DC, AC ⊥ BD, ∠CAD = θ. Then the angle ∠ABC = (SSC CGL 1st Sit. 2013)- a)θ
- b)2/θ
- c)2θ
- d)3θ
Correct answer is option 'C'. Can you explain this answer?
A cyclic quadrilateral ABCD is such that AB = BC, AD = DC, AC ⊥ BD, ∠CAD = θ. Then the angle ∠ABC = (SSC CGL 1st Sit. 2013)
a)
θ
b)
2/θ
c)
2θ
d)
3θ
|
|
Nilesh Banerjee answered |
In a cyclic quadrilateral, the opposite angles are supplementary, so ∠ABC + ∠ADC = 180°.
Since AB = BC, we can conclude that ∠ABC = ∠BCA.
Similarly, since AD = DC, we can conclude that ∠ADC = ∠ACD.
Therefore, we have ∠ABC + ∠ADC = ∠BCA + ∠ACD = 180°.
Since ∠BCA + ∠ACD = 180°, we can conclude that ∠BCA = ∠ACD = 90°.
Thus, we have proven that the diagonals of the cyclic quadrilateral are perpendicular to each other.
Since AB = BC, we can conclude that ∠ABC = ∠BCA.
Similarly, since AD = DC, we can conclude that ∠ADC = ∠ACD.
Therefore, we have ∠ABC + ∠ADC = ∠BCA + ∠ACD = 180°.
Since ∠BCA + ∠ACD = 180°, we can conclude that ∠BCA = ∠ACD = 90°.
Thus, we have proven that the diagonals of the cyclic quadrilateral are perpendicular to each other.
A, O, B are three points on a line segment and C is a point not lying on AOB. If ∠AOC = 40° and OX, OY are the internal and external bisectors of ∠AOC respectively, then ∠BOY is (SSC CGL 1st Sit. 2012)- a)70°
- b)80°
- c)72°
- d)68°
Correct answer is option 'A'. Can you explain this answer?
A, O, B are three points on a line segment and C is a point not lying on AOB. If ∠AOC = 40° and OX, OY are the internal and external bisectors of ∠AOC respectively, then ∠BOY is (SSC CGL 1st Sit. 2012)
a)
70°
b)
80°
c)
72°
d)
68°
|
|
Vikram Mehta answered |
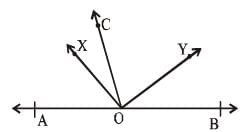
OX is the bisector of ∠AOC.
∴ ∠AOC = 2 ∠COX
OY is the bisector of ∠BOC.
∴ ∠BOC = 2 ∠COY
∴ ∠AOC + ∠BOC
= 2∠COY + 2∠COX = 180°
⇒ 2 (∠COX + ∠YOC) = 180°
⇒ ∠XOY = 90°
∴ ∠AOX + ∠XOY + ∠BOY = 180°
∴ ∠BOY = 180° – 90° – 20° = 70°
In a quadrilateral ABCD, the bisectors of ∠A and ∠B meet at O. If ∠C = 70° and ∠D = 130°, then measure of ∠AOB is (SSC CGL 1st Sit. 2014)- a)40°
- b)60°
- c)80°
- d)100°
Correct answer is option 'D'. Can you explain this answer?
In a quadrilateral ABCD, the bisectors of ∠A and ∠B meet at O. If ∠C = 70° and ∠D = 130°, then measure of ∠AOB is (SSC CGL 1st Sit. 2014)
a)
40°
b)
60°
c)
80°
d)
100°
|
|
Mira Sharma answered |
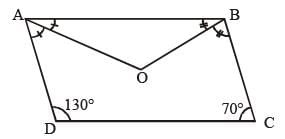
A + B + C + D = 360
A + B = 360 – (130 + 70) = 160°
∠ AOB = 180° – 80° = 100°
A and B are two points on a circle with centre O. AT is a tangent, such that ∠BAT = 45º. N is a point on OA, such that BN = 10 cm. The length of the median OM of the Δ NOB is : (SSC CHSL-2018)- a)10√2 cm
- b)5√2 cm
- c)5√3 cm
- d)5 cm
Correct answer is option 'D'. Can you explain this answer?
A and B are two points on a circle with centre O. AT is a tangent, such that ∠BAT = 45º. N is a point on OA, such that BN = 10 cm. The length of the median OM of the Δ NOB is : (SSC CHSL-2018)
a)
10√2 cm
b)
5√2 cm
c)
5√3 cm
d)
5 cm

|
EduRev SSC CGL answered |
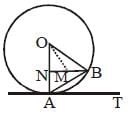
As AT is a tangent ∴∠ OAT = 90°
Again ∠ BAT = 45°
∴ ∠ OAB = 90° – 45° = 45°
In Δ AOB, OA = OB,
∴ ∠ OAB = ∠ OBA = 45° then ∠ NOB= 180° – 45° – 45° = 90° and Δ BON is also a right angle triangle.
Now, OM is a median of ΔBON,
∴ OM divide BN in two equal part
∴ BM = OM = 5 cm
If in a triangle ABC, BE and CF are two medians perpendicular to each other and if AB = 19cm and AC = 22cm then the length of BC is: (SSC Sub. Ins. 2015)- a)20.5cm
- b)19.5cm
- c)13cm
- d)26cm
Correct answer is option 'C'. Can you explain this answer?
If in a triangle ABC, BE and CF are two medians perpendicular to each other and if AB = 19cm and AC = 22cm then the length of BC is: (SSC Sub. Ins. 2015)
a)
20.5cm
b)
19.5cm
c)
13cm
d)
26cm
|
|
Mira Sharma answered |

From question, median BE ⊥ CF.
In this case we know that
(AB)2 + (AC)2 = 5 (BC)2
(19)2 + (22)2 = 5 (BC)2
361 + 484 = 5 (BC)2
845 = 5 (BC)2
BC = √169 = 13 cm
Chapter doubts & questions for Geometry - SSC CGL Mathematics Previous Year Paper (Topic-wise) 2025 is part of SSC CGL exam preparation. The chapters have been prepared according to the SSC CGL exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for SSC CGL 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Geometry - SSC CGL Mathematics Previous Year Paper (Topic-wise) in English & Hindi are available as part of SSC CGL exam.
Download more important topics, notes, lectures and mock test series for SSC CGL Exam by signing up for free.
SSC CGL Mathematics Previous Year Paper (Topic-wise)
21 docs|55 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily