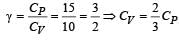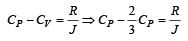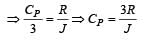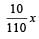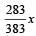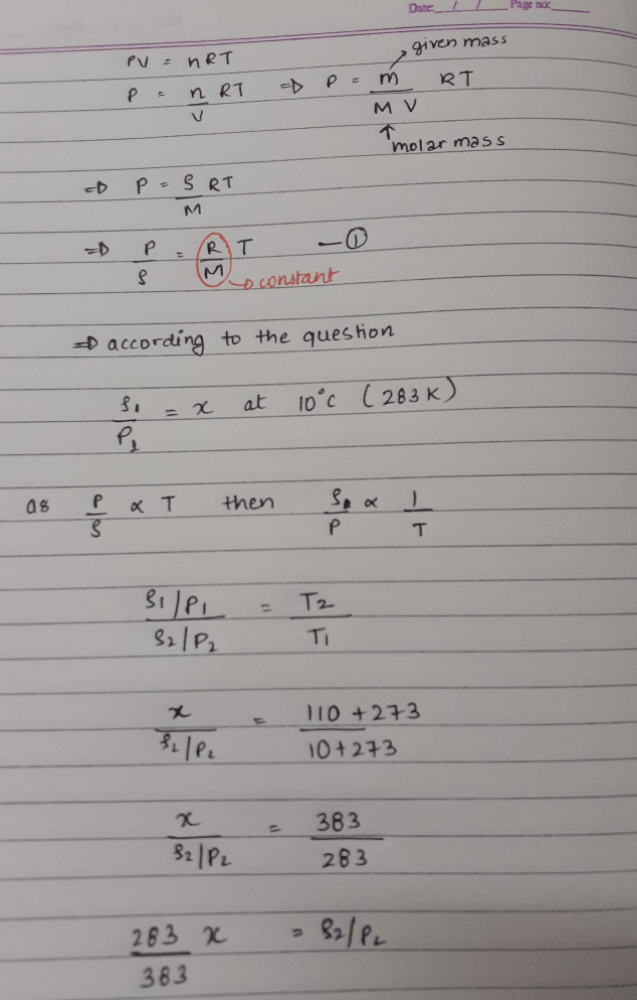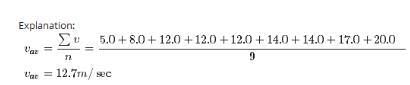All Exams >
NEET >
Physics Class 11 >
All Questions
All questions of Kinetic Theory for NEET Exam
Value of gas constant, R for one mole of a gas is independent of the- a)Atomicity of the gas
- b)Mass of gas
- c)Distance between two molecules of gas at 273 K
- d)Volume of gas
Correct answer is option 'A'. Can you explain this answer?
Value of gas constant, R for one mole of a gas is independent of the
a)
Atomicity of the gas
b)
Mass of gas
c)
Distance between two molecules of gas at 273 K
d)
Volume of gas

|
Trisha Vashisht answered |
We know that PV=nRT also PM=dRT
So in the equation The value of R depends on P , V , n , T , d , M
except atomicity
so the ans is A
So in the equation The value of R depends on P , V , n , T , d , M
except atomicity
so the ans is A
The kinetic energy of one mole of an ideal gas is E=3/2 RT. Then Cρ will be- a)0.5 R
- b)1.5 R
- c)2.5 R
- d)2.2 R
Correct answer is option 'C'. Can you explain this answer?
The kinetic energy of one mole of an ideal gas is E=3/2 RT. Then Cρ will be
a)
0.5 R
b)
1.5 R
c)
2.5 R
d)
2.2 R
|
|
Naina Sharma answered |
We know that,
Cp=cv+R
E=3Rt/2
also,
E=Cv
cp=R+3RT/2
=5/2 RT
=2.5R
Cp=cv+R
E=3Rt/2
also,
E=Cv
cp=R+3RT/2
=5/2 RT
=2.5R
A region of the earth’s atmosphere contains n molecules (treated as ideal gas molecules) per unit volume. The temperature of air in the region is T. If k represents Boltzmann’s constant and R represents universal gas constant, the pressure of air in the region is- a)RT/n
- b)nRkT
- c)nkT
- d)nT/k
Correct answer is option 'C'. Can you explain this answer?
A region of the earth’s atmosphere contains n molecules (treated as ideal gas molecules) per unit volume. The temperature of air in the region is T. If k represents Boltzmann’s constant and R represents universal gas constant, the pressure of air in the region is
a)
RT/n
b)
nRkT
c)
nkT
d)
nT/k
|
|
Lavanya Menon answered |
PV = nRT
Where n = number of moles = m/NA
So, P = (m/V)(R/NA)T
Also, we know that R/NA = k
So, P = nkT
Where n = number of moles = m/NA
So, P = (m/V)(R/NA)T
Also, we know that R/NA = k
So, P = nkT
In the case of real gases, the equation of state, PV = RT (where P, V and T are respectively the pressure, volume and absolute temperature), is strictly satisfied only if corrections are applied to the measured pressure P and the measured volume V. The corrections for P and V arise respectively due to- a)kinetic energy of molecules and collision of molecules
- b)size of molecules and expansion of the container
- c)expansion of the container and intermolecular attraction
- d)intermolecular attraction and the size of molecules
Correct answer is 'D'. Can you explain this answer?
In the case of real gases, the equation of state, PV = RT (where P, V and T are respectively the pressure, volume and absolute temperature), is strictly satisfied only if corrections are applied to the measured pressure P and the measured volume V. The corrections for P and V arise respectively due to
a)
kinetic energy of molecules and collision of molecules
b)
size of molecules and expansion of the container
c)
expansion of the container and intermolecular attraction
d)
intermolecular attraction and the size of molecules

|
Ashish Mishra answered |
D is correct
Oxygen and nitrogen in two enclosures have the same mass, volume and pressure. The ratio of the temperature of oxygen to that of nitrogen is:- a)8/7
- b)49/64
- c)1
- d)7/8
Correct answer is option 'A'. Can you explain this answer?
Oxygen and nitrogen in two enclosures have the same mass, volume and pressure. The ratio of the temperature of oxygen to that of nitrogen is:
a)
8/7
b)
49/64
c)
1
d)
7/8
|
|
Neha Joshi answered |
For same mass the ratio of moles of oxygen to that of nitrogen is 14:16 = 7:8
And we know that PV = nRT
Hence as V and P are also same, ratio of temperature of oxygen to that of nitrogen is inverse of the ratio of moles that is 8:7
And we know that PV = nRT
Hence as V and P are also same, ratio of temperature of oxygen to that of nitrogen is inverse of the ratio of moles that is 8:7
Three moles of an ideal monoatomic gas is initially in the state A shown in the adjoining pressure-temperature graph. It is taken to state B without changing its pressure. If R is the universal gas constant, the work done by the gas in this process is
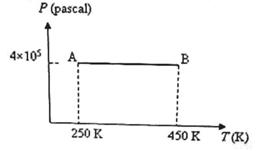
- a)600 R
- b)400 R
- c)300 R
- d)200 R
Correct answer is option 'A'. Can you explain this answer?
Three moles of an ideal monoatomic gas is initially in the state A shown in the adjoining pressure-temperature graph. It is taken to state B without changing its pressure. If R is the universal gas constant, the work done by the gas in this process is


a)
600 R
b)
400 R
c)
300 R
d)
200 R

|
Infinity Academy answered |
The work done by the gas in taking it from state A to state B = PΔV where ΔW is the increase in volume at constant pressure P.
We have PV = μRT where p is the number of moles in the sample of the gas and R is the universal gas constant.
Therefore we have PΔV = μR ΔT = 3 xR(450 - 250) = 600R
Which one of the following quantities can be zero on an average for the molecules of an ideal gas in equilibrium?- a)Speed
- b)Momentum
- c)Kinetic Energy
- d)Density
Correct answer is 'B'. Can you explain this answer?
Which one of the following quantities can be zero on an average for the molecules of an ideal gas in equilibrium?
a)
Speed
b)
Momentum
c)
Kinetic Energy
d)
Density
|
|
Riya Banerjee answered |
In case of ideal gases the average velocity is always zero. Hence the average momentum is zero.
Whereas average speed is non- zero so the kinetic energy is also non-zero, as these two are scalar quantities.
Whereas average speed is non- zero so the kinetic energy is also non-zero, as these two are scalar quantities.
The number of translational degrees of freedom for a diatomic gas is [1993]- a)2
- b)3
- c)5
- d)6
Correct answer is option 'B'. Can you explain this answer?
The number of translational degrees of freedom for a diatomic gas is [1993]
a)
2
b)
3
c)
5
d)
6

|
Prisha Singh answered |
Number of translational degrees of freedom are same for all types of gases.
The degree of freedom of a molecule of a triatomic ga s is[1999]- a)2
- b)4
- c)6
- d)8
Correct answer is option 'C'. Can you explain this answer?
The degree of freedom of a molecule of a triatomic ga s is[1999]
a)
2
b)
4
c)
6
d)
8

|
Krish Khanna answered |
No. of degree of freedom = 3 K – N where K is no. of atom and N is the number of relations between atoms. For triatomic gas, K = 3, N = 3C2 = 3
No. of degree of freedom = 3 (3) – 3 = 6
No. of degree of freedom = 3 (3) – 3 = 6
How many degrees of freedom do non linear triatomic gas molecules has?- a)two
- b)six
- c)three
- d)five
Correct answer is option 'B'. Can you explain this answer?
How many degrees of freedom do non linear triatomic gas molecules has?
a)
two
b)
six
c)
three
d)
five
|
|
Hansa Sharma answered |
A triatomic nonlinear gaseous atom has 6 degrees of freedom, that are 3 in all transrational directions and three rotational barriers in all the three axises.
The number of degrees of freedom a diatomic molecule is- a)6
- b)5.0
- c)3
- d)5.3
Correct answer is option 'D'. Can you explain this answer?
The number of degrees of freedom a diatomic molecule is
a)
6
b)
5.0
c)
3
d)
5.3

|
Akshara Chopra answered |
Explanation:Degrees of freedom of a system refers to the possible independent motions a system can have.the total degrees of freedom describing the motion of a diatomic molecule is 5.3 for translation and 2 for rotation
Four moles of an ideal diatomic gas is heated at constant volume from 20° C to 30° C. The molar specific heat of the gas at constant pressure (Cp) is 30.3 Jmol-1K-1 and the universal gas constant (R) is 8.3 Jmol-1K-1. The increase in internal energy of the gas is- a)332 J
- b)80.3 J
- c)303 J
- d)880 J
Correct answer is 'D'. Can you explain this answer?
Four moles of an ideal diatomic gas is heated at constant volume from 20° C to 30° C. The molar specific heat of the gas at constant pressure (Cp) is 30.3 Jmol-1K-1 and the universal gas constant (R) is 8.3 Jmol-1K-1. The increase in internal energy of the gas is
a)
332 J
b)
80.3 J
c)
303 J
d)
880 J
|
|
Raghav Bansal answered |
The value of Cp is 30.3
and as Cp-Cv = R(8.3)
hence Cv = 30.3-8.3
Cv is 22
change in internal energy = no of moles × Cv × change in temperature
hence
change in internal energy = 22 × 4 × 10
= 880j
Hence Option D is correct.
and as Cp-Cv = R(8.3)
hence Cv = 30.3-8.3
Cv is 22
change in internal energy = no of moles × Cv × change in temperature
hence
change in internal energy = 22 × 4 × 10
= 880j
Hence Option D is correct.
Kinetic theory explains the behavior- a)of liquids based on the idea that the liquids consist of rapidly moving atoms or molecules
- b)of gases based on the idea that the gas consists of rapidly moving atoms or molecules
- c)of solids based on the idea that the solid consists of rapidly vibrating atoms or molecules
- d)of solids and liquids based on the idea that they gas consist of rapidly vibrating atoms or molecules
Correct answer is option 'B'. Can you explain this answer?
Kinetic theory explains the behavior
a)
of liquids based on the idea that the liquids consist of rapidly moving atoms or molecules
b)
of gases based on the idea that the gas consists of rapidly moving atoms or molecules
c)
of solids based on the idea that the solid consists of rapidly vibrating atoms or molecules
d)
of solids and liquids based on the idea that they gas consist of rapidly vibrating atoms or molecules
|
|
Shreya Gupta answered |
Kinetic theory explains the behaviour of gases based on the idea that the gas consists of rapidly moving atoms or molecules. This is possible as the inter-atomic forces, which are short range forces that are important for solids and liquids, can be neglected for gases.
Mean free path is the- a)maximum distance between collisions
- b)minimum distance between collisions
- c)average distance between collisions
- d)(maximum distance + minimum distance )/ 2 between collisions
Correct answer is option 'C'. Can you explain this answer?
Mean free path is the
a)
maximum distance between collisions
b)
minimum distance between collisions
c)
average distance between collisions
d)
(maximum distance + minimum distance )/ 2 between collisions

|
Kaavya Mukherjee answered |
Explanation:the mean free path is the average distance traveled by a moving particle (such as an atom, a molecule, a photon) between successive impacts (collisions), which modify its direction or energy or other particle properties.
According to kinetic theory of gases, 0K is that temperature at which for an ideal gas- a)pressure is not zero
- b)internal energy is zero
- c)nearly all molecular motion becomes very rapid
- d)volume is not zero
Correct answer is option 'B'. Can you explain this answer?
According to kinetic theory of gases, 0K is that temperature at which for an ideal gas
a)
pressure is not zero
b)
internal energy is zero
c)
nearly all molecular motion becomes very rapid
d)
volume is not zero

|
Sara Saldi answered |
Because at temperature 0K nearly all molecular motion happen to stop. insisting the internal energy to be simple.
I hope it helped
I hope it helped
At absolute zero temperature may be defined as that temperature at which- a)Volume is maximum
- b)Root mean square velocity of the gas molecule reduces to zero
- c)Temperature is 273 K
- d)Mass of molecules of gas is zero
Correct answer is option 'B'. Can you explain this answer?
At absolute zero temperature may be defined as that temperature at which
a)
Volume is maximum
b)
Root mean square velocity of the gas molecule reduces to zero
c)
Temperature is 273 K
d)
Mass of molecules of gas is zero
|
|
Gaurav Kumar answered |
At 0K temperature we know that there is no molecular motion, that is the KE of the particles gets 0. Thus we can say the combined KE of a gaseous system is zero, but as there combined mass cant be zero thus the combined of the square of velocities of the particles is zero, which means that the root mean square velocity of the gas is zero.
According to kinetic theory of gases, at absolute zero temperature [1990]- a)water freezes
- b)liquid helium freezes
- c)molecular motion stops
- d)liquid hydrogen freezes
Correct answer is option 'C'. Can you explain this answer?
According to kinetic theory of gases, at absolute zero temperature [1990]
a)
water freezes
b)
liquid helium freezes
c)
molecular motion stops
d)
liquid hydrogen freezes
|
|
Nirvikar Shakya answered |
See it is assumption only that at absolute zero temperature i.e 0 K temperature all type of molecular motion stopes since at earth it is impossible to achieve 0 K temp so i said it is mearly a assumption only . Though it is clear that all materials freeze at absolute 0 temperature so clearly water, liquid helium and liquid Hydrogen they all freezes . BUT ACCORDING TO THEORY OPTION C SEEMS TO BE MORE ACCURATE.
The degree of freedom for tri atomic gas is:- a)6
- b)4
- c)5
- d)3
Correct answer is option 'A'. Can you explain this answer?
The degree of freedom for tri atomic gas is:
a)
6
b)
4
c)
5
d)
3
|
|
Hansa Sharma answered |
Degrees of freedom are the ways in which a molecule of the gas can execute motion.
So in case of triatomic gas molecule:
1. It can translate (move) in all 3 dimensions, which accounts for 3 degrees of freedom (since there are 3 dimensions in which it could translate (move)).
2. This molecule can also revolve with Moment of Inertia ≠ 0 around all three axes, x, y, and z, which accounts for another 3 degrees of freedom (since there are 3 axes of rotation).
So in case of triatomic gas molecule:
1. It can translate (move) in all 3 dimensions, which accounts for 3 degrees of freedom (since there are 3 dimensions in which it could translate (move)).
2. This molecule can also revolve with Moment of Inertia ≠ 0 around all three axes, x, y, and z, which accounts for another 3 degrees of freedom (since there are 3 axes of rotation).
If a gas has n degree of freedom, ratio of principal specific heats of the gas is- a)1+ 2/n
- b)2n
- c)1 - 2/n
- d)-2n
Correct answer is option 'A'. Can you explain this answer?
If a gas has n degree of freedom, ratio of principal specific heats of the gas is
a)
1+ 2/n
b)
2n
c)
1 - 2/n
d)
-2n
|
|
Pooja Shah answered |
Let us consider 1 mole of an ideal gas at kelvin temperature T. It has N molecules (Avogadro's number). The internal energy of an ideal gas is entirely kinetic. The average KE per molecule of a ideal gas is ½ nkT (k is boltzman constant), where n is degree of freedom. Therefore, the internal energy of one mole of a gas would be
E=N(1/2nKT)=1/2nRT (∵k=R/N)
Now, Cv=dE/dT=n/2 R
and Cp=n/2 R+R=(n/2+1)R
Cp/ Cv =(n/2+1)R/n/2=(1+2/n)
E=N(1/2nKT)=1/2nRT (∵k=R/N)
Now, Cv=dE/dT=n/2 R
and Cp=n/2 R+R=(n/2+1)R
Cp/ Cv =(n/2+1)R/n/2=(1+2/n)
The average distance a molecule can travel without colliding is called- a)Average distance
- b)Mean free path
- c)Mean drift
- d)Mean distance
Correct answer is option 'B'. Can you explain this answer?
The average distance a molecule can travel without colliding is called
a)
Average distance
b)
Mean free path
c)
Mean drift
d)
Mean distance
|
|
Rajat Patel answered |
Mean free path is the average distance between the two successive collisions. Inside the gas there are several molecules which are randomly moving and colliding with each other. The distance which a particular gas molecule travels without colliding is known as mean free path.
When the temperature goes up, the pressure inside a rigid container will _____.- a)remain unchanged
- b)go down
- c)cause particles to cool
- d)go up
Correct answer is option 'D'. Can you explain this answer?
When the temperature goes up, the pressure inside a rigid container will _____.
a)
remain unchanged
b)
go down
c)
cause particles to cool
d)
go up
|
|
Vijay Bansal answered |
The pressure law states that for a constant volume of gas in a sealed container the temperature of the gas is directly proportional to its pressure. This can be easily understood by visualising the particles of gas in the container moving with a greater energy when the temperature is increased.
In a vessel, the gas is at a pressure P. If the mass of all the molecules is halved and their speed is doubled, then the resultant pressure will be [NEET Kar. 2013]- a)4P
- b)2P
- c)P
- d)P/2
Correct answer is option 'B'. Can you explain this answer?
In a vessel, the gas is at a pressure P. If the mass of all the molecules is halved and their speed is doubled, then the resultant pressure will be [NEET Kar. 2013]
a)
4P
b)
2P
c)
P
d)
P/2

|
Krish Chakraborty answered |
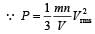
When mass is halved and speed is doubled then Resultant pressure,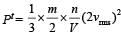 = 2 P.
= 2 P.
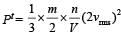 = 2 P.
= 2 P.One mole of hydrogen gas is heated at constant pressure from 300 K to 420 K. Calculate the increase in its internal energy.- a)2.49 kJ
- b)2.65 kJ
- c)2.15 kJ
- d)2.85 kJ
Correct answer is option 'A'. Can you explain this answer?
One mole of hydrogen gas is heated at constant pressure from 300 K to 420 K. Calculate the increase in its internal energy.
a)
2.49 kJ
b)
2.65 kJ
c)
2.15 kJ
d)
2.85 kJ

|
Madhurima Dasgupta answered |
Explanation:
Hydrogen is a diatomic gas. (CV = 2.5R)
Change in internal energy
ΔU = nCVΔT = 1 x 2.5 x 8.31 x 120 = 2493J = 2.49KJ
Calculate the change in internal energy of 3.00 mol of helium gas when its temperature is increased by 2.00 K.- a)85.0 J
- b)95.0 J
- c)65.0 J
- d)75.0 J
Correct answer is option 'D'. Can you explain this answer?
Calculate the change in internal energy of 3.00 mol of helium gas when its temperature is increased by 2.00 K.
a)
85.0 J
b)
95.0 J
c)
65.0 J
d)
75.0 J
|
|
Athira Chavan answered |
Understanding Internal Energy Change
The internal energy change (ΔU) of an ideal gas can be calculated using the formula:
ΔU = n * C_v * ΔT
Where:
- n = number of moles
- C_v = molar specific heat at constant volume
- ΔT = change in temperature
Parameters for Helium Gas
- Helium is a monoatomic ideal gas.
- For monoatomic gases, C_v is approximately 3/2 R, where R is the ideal gas constant (8.314 J/mol·K).
Calculation Steps
1. Identify Variables:
- n = 3.00 mol (given)
- C_v = (3/2) * R = (3/2) * 8.314 J/mol·K = 12.471 J/mol·K
- ΔT = 2.00 K (given)
2. Plug in Values:
ΔU = n * C_v * ΔT
ΔU = 3.00 mol * 12.471 J/mol·K * 2.00 K
3. Perform the Calculation:
- ΔU = 3.00 * 12.471 * 2.00
- ΔU = 3.00 * 24.942
- ΔU = 74.826 J (approximately 75.0 J)
Conclusion
The calculated change in internal energy for 3.00 mol of helium gas when the temperature is increased by 2.00 K is approximately 75.0 J. Therefore, the correct answer is option 'D', which aligns with the calculated value.
The internal energy change (ΔU) of an ideal gas can be calculated using the formula:
ΔU = n * C_v * ΔT
Where:
- n = number of moles
- C_v = molar specific heat at constant volume
- ΔT = change in temperature
Parameters for Helium Gas
- Helium is a monoatomic ideal gas.
- For monoatomic gases, C_v is approximately 3/2 R, where R is the ideal gas constant (8.314 J/mol·K).
Calculation Steps
1. Identify Variables:
- n = 3.00 mol (given)
- C_v = (3/2) * R = (3/2) * 8.314 J/mol·K = 12.471 J/mol·K
- ΔT = 2.00 K (given)
2. Plug in Values:
ΔU = n * C_v * ΔT
ΔU = 3.00 mol * 12.471 J/mol·K * 2.00 K
3. Perform the Calculation:
- ΔU = 3.00 * 12.471 * 2.00
- ΔU = 3.00 * 24.942
- ΔU = 74.826 J (approximately 75.0 J)
Conclusion
The calculated change in internal energy for 3.00 mol of helium gas when the temperature is increased by 2.00 K is approximately 75.0 J. Therefore, the correct answer is option 'D', which aligns with the calculated value.
One mole of hydrogen gas is heated at constant pressure from 300 K to 420 K. Calculate the energy transferred by heat to the gas- a)3.86 kJ
- b)3.49 kJ
- c)3.66 kJ
- d)3.26 kJ
Correct answer is option 'B'. Can you explain this answer?
One mole of hydrogen gas is heated at constant pressure from 300 K to 420 K. Calculate the energy transferred by heat to the gas
a)
3.86 kJ
b)
3.49 kJ
c)
3.66 kJ
d)
3.26 kJ

|
Krithika Kulkarni answered |
Explanation:
Hydrogen is a diatomic gas. (CP = 3.5R)
energy transferred by heat to the gas
Q=nCPΔT=1×3.5×8.31×120=3490J=3.49KJ
In which case are the atoms relatively rigidly fixed?- a)gases
- b)liquids and gases
- c)solids
- d)liquids
Correct answer is option 'C'. Can you explain this answer?
In which case are the atoms relatively rigidly fixed?
a)
gases
b)
liquids and gases
c)
solids
d)
liquids

|
Pranav Saha answered |
Explanation:
Atoms in a gas are well separated with no regular arrangement. Atoms vibrate and move freely at high speeds
Atoms in a liquid are close together with no regular arrangement. Atoms vibrate, move about, and slide past each other.
Atoms in a solid are tightly packed, usually in a regular pattern. Atoms vibrate (jiggle) but generally do not move from place to place.
1calorie = ?
- a)4148 Joules
- b)414.8 Joules
- c)4.8 Joules
- d)4.184 Joules
Correct answer is option 'D'. Can you explain this answer?
1calorie = ?
a)
4148 Joules
b)
414.8 Joules
c)
4.8 Joules
d)
4.184 Joules
|
|
Priya Patel answered |
1 calorie = 4.184 joules. That is the conversion rate, no explanation.
The amount of heat energy required to raise the temperature of 1g of Helium at NTP, from T1K to T2K is [NEET 2013]- a)
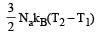
- b)
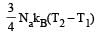
- c)

- d)

Correct answer is option 'D'. Can you explain this answer?
The amount of heat energy required to raise the temperature of 1g of Helium at NTP, from T1K to T2K is [NEET 2013]
a)
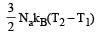
b)
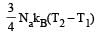
c)

d)


|
Abhishek Desai answered |
From first law of thermodynamics ΔQ = ΔU + ΔW
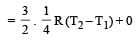
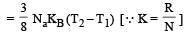
Kinetic theory relates measurable properties.- a)of liquids such as viscosity, conduction and diffusion with molecular parameters, yielding estimates of molecular sizes and masses
- b)of super cooled liquids such as viscosity, creep and diffusion with molecular parameters, yielding estimates of molecular sizes and masses
- c)of solids such as expansion, conduction and elongation with molecular parameters, yielding estimates of molecular sizes and masses
- d)of gases such as viscosity, conduction and diffusion with molecular parameters, yielding estimates of molecular sizes and masses
Correct answer is option 'D'. Can you explain this answer?
Kinetic theory relates measurable properties.
a)
of liquids such as viscosity, conduction and diffusion with molecular parameters, yielding estimates of molecular sizes and masses
b)
of super cooled liquids such as viscosity, creep and diffusion with molecular parameters, yielding estimates of molecular sizes and masses
c)
of solids such as expansion, conduction and elongation with molecular parameters, yielding estimates of molecular sizes and masses
d)
of gases such as viscosity, conduction and diffusion with molecular parameters, yielding estimates of molecular sizes and masses

|
Moumita Chakraborty answered |
Explanation:Kinetic theory explains the behaviour of gases based on the idea that the gas consists of rapidly moving atoms or molecules. It also relates measurable properties of gases such as viscosity, conduction and diffusion with molecular parameters, yielding estimates of molecular sizes and masses.
One mole of an ideal monatomic gas is at an initial temperature of 300 K. The gas undergoes an isovolumetric process, acquiring 500 J of energy by heat. It then undergoes an isobaric process, losing this same amount of energy by heat. Determine the work done on the gas.- a)123 J
- b)231 J
- c)333 J
- d)200 J
Correct answer is option 'D'. Can you explain this answer?
One mole of an ideal monatomic gas is at an initial temperature of 300 K. The gas undergoes an isovolumetric process, acquiring 500 J of energy by heat. It then undergoes an isobaric process, losing this same amount of energy by heat. Determine the work done on the gas.
a)
123 J
b)
231 J
c)
333 J
d)
200 J

|
Aniket Basu answered |
Explanation:
At const volume,
Q = 500 J
Q=nCPΔT
500=1×2.5×8.31ΔT
ΔT=24.06
W=nRΔT=1×8.31×24.06=200J
Four liters of a diatomic ideal gas ( λ =1.4) confined to a cylinder is subject to a closed cycle. Initially, the gas is at 1.00 atm and at 300 K. First, its pressure is tripled under constant volume. Then, it expands adiabatically to its original pressure. Finally, the gas is compressed isobarically to its original volume. Find the temperature at the end of the cycle- a)276 K
- b)285 K
- c)300 K
- d)332 K
Correct answer is option 'C'. Can you explain this answer?
Four liters of a diatomic ideal gas ( λ
=1.4
) confined to a cylinder is subject to a closed cycle. Initially, the gas is at 1.00 atm and at 300 K. First, its pressure is tripled under constant volume. Then, it expands adiabatically to its original pressure. Finally, the gas is compressed isobarically to its original volume. Find the temperature at the end of the cyclea)
276 K
b)
285 K
c)
300 K
d)
332 K

|
Anshu Joshi answered |
According to Atomic Hypothesis: little particles of atom- a)attract each other when they are at small distance apart, but repel upon being squeezed into one another
- b)repel each other when they are at small distance apart, but attract upon being squeezed into one another
- c)repel each other when they are at small distance apart, but repel upon being squeezed into one another
- d)repel each other when they are at large distance apart, but attract upon being separated from one another
Correct answer is option 'A'. Can you explain this answer?
According to Atomic Hypothesis: little particles of atom
a)
attract each other when they are at small distance apart, but repel upon being squeezed into one another
b)
repel each other when they are at small distance apart, but attract upon being squeezed into one another
c)
repel each other when they are at small distance apart, but repel upon being squeezed into one another
d)
repel each other when they are at large distance apart, but attract upon being separated from one another

|
Saikat Sharma answered |
Explanation:At room temperature (=300K) the noble gases are all in the gas phase, they are banging around and colliding into one another like little pool balls. At this temperature, when the atoms collide they appear to elastically bounce off of one another, but this bounce is actually a result of atomic repulsion. The atoms are traveling so fast and they approach each other so quickly that their momentum 'squeezes' them together until the atomic repulsion pushes them back apart.
The average kinetic energy of a molecule in an ideal gas is- a)proportional to the pressure
- b)depends on the nature of the ideal gas
- c)proportional to the absolute temperature of the gas
- d)proportional to the volume
Correct answer is option 'C'. Can you explain this answer?
The average kinetic energy of a molecule in an ideal gas is
a)
proportional to the pressure
b)
depends on the nature of the ideal gas
c)
proportional to the absolute temperature of the gas
d)
proportional to the volume
|
|
Priya Patel answered |
SHOW THAT THE AVERAGE TRANSLATIONAL KINETIC ENERGY OF THE MOLECULES OF A GAS IS DIRECTLY PROPORTIONAL TO ABSOLUTE TEMPERATURE. kinetic energy of the molecules of a gas is directly proportional to absolute temperature.
The mean free path is the ____________- a)average distance covered by a molecule between two successive collisions
- b)length of the container that contains the gas
- c)mean of the square of the average distance between two successive collisions
- d)square of the average distance between two successive collisions
Correct answer is option 'A'. Can you explain this answer?
The mean free path is the ____________
a)
average distance covered by a molecule between two successive collisions
b)
length of the container that contains the gas
c)
mean of the square of the average distance between two successive collisions
d)
square of the average distance between two successive collisions
|
|
Anushka Das answered |
Mean Free Path
The mean free path is a concept used in physics to describe the average distance traveled by a molecule or particle between two successive collisions. It is an important parameter in the study of gas behavior and is particularly relevant in the kinetic theory of gases.
Definition
The mean free path can be defined as the average distance covered by a molecule between two successive collisions. It represents the average distance a molecule travels before it interacts with another molecule or particle in a gas.
Explanation
To understand why the correct answer is option 'A', let's consider the behavior of gas molecules in a container. The gas molecules are in constant motion, moving in straight lines until they collide with other molecules or the walls of the container.
Each time a molecule collides with another molecule or the walls, its direction and velocity may change. The time it takes for a molecule to collide again depends on its speed and the density of the gas. Molecules with higher speeds will collide more frequently, while molecules in a denser gas will also collide more frequently.
The mean free path is an average value, calculated by considering the total distance covered by all the molecules in a gas and dividing it by the total number of collisions. Since the molecules move in random directions, the actual path of each molecule may be different.
Importance
The mean free path is a fundamental parameter in the kinetic theory of gases and is used to characterize the behavior of gas molecules. It provides valuable information about the average distance traveled by molecules, which is important for understanding diffusion, heat conduction, and other transport phenomena in gases.
Conclusion
In conclusion, the mean free path is the average distance covered by a molecule between two successive collisions. It is an important parameter in the study of gas behavior and helps to describe the motion and interactions of gas molecules. Option 'A' is the correct answer because it accurately defines the mean free path.
The mean free path is a concept used in physics to describe the average distance traveled by a molecule or particle between two successive collisions. It is an important parameter in the study of gas behavior and is particularly relevant in the kinetic theory of gases.
Definition
The mean free path can be defined as the average distance covered by a molecule between two successive collisions. It represents the average distance a molecule travels before it interacts with another molecule or particle in a gas.
Explanation
To understand why the correct answer is option 'A', let's consider the behavior of gas molecules in a container. The gas molecules are in constant motion, moving in straight lines until they collide with other molecules or the walls of the container.
Each time a molecule collides with another molecule or the walls, its direction and velocity may change. The time it takes for a molecule to collide again depends on its speed and the density of the gas. Molecules with higher speeds will collide more frequently, while molecules in a denser gas will also collide more frequently.
The mean free path is an average value, calculated by considering the total distance covered by all the molecules in a gas and dividing it by the total number of collisions. Since the molecules move in random directions, the actual path of each molecule may be different.
Importance
The mean free path is a fundamental parameter in the kinetic theory of gases and is used to characterize the behavior of gas molecules. It provides valuable information about the average distance traveled by molecules, which is important for understanding diffusion, heat conduction, and other transport phenomena in gases.
Conclusion
In conclusion, the mean free path is the average distance covered by a molecule between two successive collisions. It is an important parameter in the study of gas behavior and helps to describe the motion and interactions of gas molecules. Option 'A' is the correct answer because it accurately defines the mean free path.
1 mole of a monoatomic gas is mixed with 3 moles of a diatomic gas. What is the molecular specific heat of the mixture at constant volume?- a)12.5 J / mol K
- b)18.7 J / mol K
- c)15.2 J / mol K
- d)22.6 J / mol K
Correct answer is option 'B'. Can you explain this answer?
1 mole of a monoatomic gas is mixed with 3 moles of a diatomic gas. What is the molecular specific heat of the mixture at constant volume?
a)
12.5 J / mol K
b)
18.7 J / mol K
c)
15.2 J / mol K
d)
22.6 J / mol K

|
Aravind Saha answered |
Explanation:
for monoatomic gas
from conservation of energy

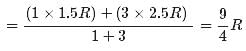
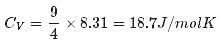
At 0 K, which of the following properties of a gas will be zero? [1996]- a)Kinetic energy
- b)Potential energy
- c)Density
- d)Ma ss
Correct answer is option 'A'. Can you explain this answer?
At 0 K, which of the following properties of a gas will be zero? [1996]
a)
Kinetic energy
b)
Potential energy
c)
Density
d)
Ma ss

|
Mahi Shah answered |
At 0 K, molecular motion stops. Hence, kinetic energy of molecules becomes zero.
One mole of an ideal monoatomic gas requires 207 J heat to raise the temperature by 10 K when heated at constant pressure. If the same gas is heated at constant volume to raise the temperature by the same 10 K, the heat required is [Given the gas constant R = 8.3 J/ mol. K] [1990]- a)198.7 J
- b)29 J
- c)215.3 J
- d)124 J
Correct answer is option 'D'. Can you explain this answer?
One mole of an ideal monoatomic gas requires 207 J heat to raise the temperature by 10 K when heated at constant pressure. If the same gas is heated at constant volume to raise the temperature by the same 10 K, the heat required is [Given the gas constant R = 8.3 J/ mol. K] [1990]
a)
198.7 J
b)
29 J
c)
215.3 J
d)
124 J

|
Ritika Khanna answered |
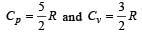
We know that Qv = nCvΔT and Qp = nCpΔT

Given Qp = 207 J 

The average kinetic energy of a molecule- a)is proportional to the absolute temperature of the gas
- b)is inversely proportional to the absolute temperature of the gas
- c)is inversely proportional to the molecular mass of the gas
- d)is not dependent on absolute temperature of the gas
Correct answer is option 'A'. Can you explain this answer?
The average kinetic energy of a molecule
a)
is proportional to the absolute temperature of the gas
b)
is inversely proportional to the absolute temperature of the gas
c)
is inversely proportional to the molecular mass of the gas
d)
is not dependent on absolute temperature of the gas

|
Sanika Shaikh answered |
We know formula ,
E/N=(3/2)kbT
the average of kinectic energy per molecules is directly proportional to the absolute temperature of gas.
Three vessels of equal capacity have gases at the same temperature and pressure. The first vessel contains neon (monatomic), the second contains chlorine (diatomic), and the third contains uranium hexafluoride (polyatomic). The number of molecules- a)is the same in all three vessels
- b)is the greatest in the vessel with neon
- c)is the greatest in the vessel with chlorine
- d)is the greatest in the vessel with uranium hexafluoride
Correct answer is option 'A'. Can you explain this answer?
Three vessels of equal capacity have gases at the same temperature and pressure. The first vessel contains neon (monatomic), the second contains chlorine (diatomic), and the third contains uranium hexafluoride (polyatomic). The number of molecules
a)
is the same in all three vessels
b)
is the greatest in the vessel with neon
c)
is the greatest in the vessel with chlorine
d)
is the greatest in the vessel with uranium hexafluoride

|
Sarthak Verma answered |
Explanation:Avogadro's law states that, "equal volumes of all gases, at the same temperature and pressure, have the same number of molecules".
Chapter doubts & questions for Kinetic Theory - Physics Class 11 2025 is part of NEET exam preparation. The chapters have been prepared according to the NEET exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Kinetic Theory - Physics Class 11 in English & Hindi are available as part of NEET exam.
Download more important topics, notes, lectures and mock test series for NEET Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup

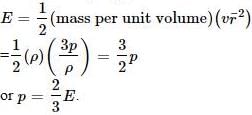


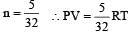 [∵ PV = nRT]
[∵ PV = nRT]