All Exams >
Bank Exams >
NABARD Grade A & Grade B Preparation >
All Questions
All questions of Exam Based Questions for Bank Exams Exam
Direction (Q. 1-5) Study the following Line Graph and table to answer the following questions. Line Graph percentage of Men and Women having Jobs in that year respectively.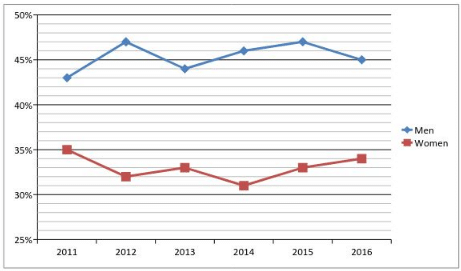
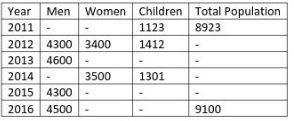 Note: Total Population = Men + Women + Children.Q. If total number of Men and Women who are doing Job in the year 2011 is 3106 then Men population in the year 2011 is?
Note: Total Population = Men + Women + Children.Q. If total number of Men and Women who are doing Job in the year 2011 is 3106 then Men population in the year 2011 is?- a)4300
- b)4400
- c)4500
- d)4600
- e)4700
Correct answer is option 'E'. Can you explain this answer?
Direction (Q. 1-5) Study the following Line Graph and table to answer the following questions. Line Graph percentage of Men and Women having Jobs in that year respectively.
Note: Total Population = Men + Women + Children.
Q.
If total number of Men and Women who are doing Job in the year 2011 is 3106 then Men population in the year 2011 is?
a)
4300
b)
4400
c)
4500
d)
4600
e)
4700
|
|
Anaya Patel answered |
M+W = 8923-1123 = 7800
43M+35W = 3106*100
Then M = 4700
43M+35W = 3106*100
Then M = 4700
In an examination, ratio of number of students who passed to number of students who failed is 5:2. If 10 more students appeared for the exam then number of students failed was 5 more than earlier, then new ratio of number of students passed to number of students failed is 7:3.Then total number of students earlier is?- a)120
- b)140
- c)160
- d)180
- e)Cannot be determined
Correct answer is option 'B'. Can you explain this answer?
In an examination, ratio of number of students who passed to number of students who failed is 5:2. If 10 more students appeared for the exam then number of students failed was 5 more than earlier, then new ratio of number of students passed to number of students failed is 7:3.Then total number of students earlier is?
a)
120
b)
140
c)
160
d)
180
e)
Cannot be determined
|
|
Preeti Khanna answered |
5x+y/2x+10-y = 7:3
and 2x+10-y- 2x =5
y =5
then x =20
total = (5+2)*20 = 140
and 2x+10-y- 2x =5
y =5
then x =20
total = (5+2)*20 = 140
Bhaskar had two sons Uday and Surya whose ages are 12 and 14 Years respectively. He deposited equal money on each of them in two different Banks which offered 6% , 8% Simple Interest to Uday and Surya respectively. Bhaskar plan is such that at certain age both of their amounts will become equal. Then at what age their amounts will be equal?- a)20
- b)21
- c)24
- d)27
- e)Cannot be determined
Correct answer is option 'A'. Can you explain this answer?
Bhaskar had two sons Uday and Surya whose ages are 12 and 14 Years respectively. He deposited equal money on each of them in two different Banks which offered 6% , 8% Simple Interest to Uday and Surya respectively. Bhaskar plan is such that at certain age both of their amounts will become equal. Then at what age their amounts will be equal?
a)
20
b)
21
c)
24
d)
27
e)
Cannot be determined

|
Power Of Learning answered |
P×6×{t+2}/100 = p×8×t/100
6(t+2) = 8t
2t= 12
t= 6 years
so age of Surya= 14+t= 14 +6= 20 years
age of Uday= 12 + (t+2)= 12 + 6+2 = 20 years
bcz surya is 2 years are older than Uday.
That's why equal S.I. gained by both takes 6 years and 8 years respectively.
so , at 20 years age both will get equal amount.
6(t+2) = 8t
2t= 12
t= 6 years
so age of Surya= 14+t= 14 +6= 20 years
age of Uday= 12 + (t+2)= 12 + 6+2 = 20 years
bcz surya is 2 years are older than Uday.
That's why equal S.I. gained by both takes 6 years and 8 years respectively.
so , at 20 years age both will get equal amount.
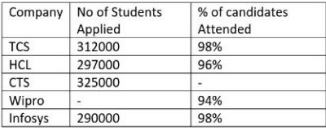
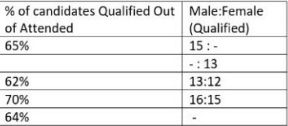 Q. In HCL, if the ratio of the number of students Attended to the number of candidates qualified is 8:5, and the number of Males qualified was 88704 then number of Females qualified is?
Q. In HCL, if the ratio of the number of students Attended to the number of candidates qualified is 8:5, and the number of Males qualified was 88704 then number of Females qualified is?- a)81168
- b)81568
- c)82068
- d)82368
- e)Cannot be determined
Correct answer is option 'D'. Can you explain this answer?
Q.
In HCL, if the ratio of the number of students Attended to the number of candidates qualified is 8:5, and the number of Males qualified was 88704 then number of Females qualified is?
a)
81168
b)
81568
c)
82068
d)
82368
e)
Cannot be determined
|
|
Aisha Gupta answered |
If the ratio of number of students Attended to number of candidates qualified is 8:5 then percentage of candidates qualified out of attended is 60%
297*96*6*(M/M+13) = 88704
M = 14
Then Females = 297*96*6*13/27 = 82368
297*96*6*(M/M+13) = 88704
M = 14
Then Females = 297*96*6*13/27 = 82368
Badri is travelling a distance of 540 Km from Place A to Place B. He covered first 1/3 rd distance by Cycle, Second 1/3 rd distance by Bike and the remaining distance by Car. The average speed of entire journey is 9 Km/hr more than the speed of the Cycle. Speed of Bike is 6 Km/hr more than Speed of Cycle, While speed of Car is 4 times that of the speed of the Cycle. Then what is the average speed of the journey?- a)27 Km/hr
- b)36 Km/hr
- c)54 Km/hr
- d)60 Km/hr
- e)Cannot be determined
Correct answer is option 'A'. Can you explain this answer?
Badri is travelling a distance of 540 Km from Place A to Place B. He covered first 1/3 rd distance by Cycle, Second 1/3 rd distance by Bike and the remaining distance by Car. The average speed of entire journey is 9 Km/hr more than the speed of the Cycle. Speed of Bike is 6 Km/hr more than Speed of Cycle, While speed of Car is 4 times that of the speed of the Cycle. Then what is the average speed of the journey?
a)
27 Km/hr
b)
36 Km/hr
c)
54 Km/hr
d)
60 Km/hr
e)
Cannot be determined
|
|
Kavya Saxena answered |
540/S = 180*(1/S-9 + 1/S-3 + 1/4*(S-9)
S = 27
S = 27
A container is filled upto 80% of its capacity with mixture of Water and Milk in the ratio of 1:3. Now 1/25 th of Mixture is taken out and 24 litres of water is added. Then the ratio of Water to Milk becomes 1:2. Then what is capacity of Jar in litre?- a)200
- b)250
- c)300
- d)400
- e)Cannot be determined
Correct answer is option 'B'. Can you explain this answer?
A container is filled upto 80% of its capacity with mixture of Water and Milk in the ratio of 1:3. Now 1/25 th of Mixture is taken out and 24 litres of water is added. Then the ratio of Water to Milk becomes 1:2. Then what is capacity of Jar in litre?
a)
200
b)
250
c)
300
d)
400
e)
Cannot be determined
|
|
Rhea Reddy answered |
(x-x/25+24)/(3x- 3x/25) = 1:2
x = 50 4x =200
capacity of jar = 250
x = 50 4x =200
capacity of jar = 250
224,?,444,1329,5312,26555- a)223
- b)224
- c)324
- d)412
- e)444
Correct answer is option 'A'. Can you explain this answer?
224,?,444,1329,5312,26555
a)
223
b)
224
c)
324
d)
412
e)
444
|
|
Ravi Singh answered |
224*1-1 = 223
223*2 -2 = 444
444*3 – 3 = 1329
1329*4 – 4 = 5312
5312*5 – 5 = 26555
223*2 -2 = 444
444*3 – 3 = 1329
1329*4 – 4 = 5312
5312*5 – 5 = 26555
In the year 2015 in VIT University the ratio of ECE, EEE and CSE are in the ratio of 6:7:8. In the year 2016 seats were increased by X%, Y% and Z% respectively in the above branches. By this the number of seats in each branch became equal. Then which of the following combination is true?- a)X = 40 Y = 15 Z = 10
- b)X = 35 Y = 20 Z = 10
- c)X = 40 Y = 25 Z = 5
- d)X = 40 Y = 20 Z = 5
- e)None
Correct answer is option 'C'. Can you explain this answer?
In the year 2015 in VIT University the ratio of ECE, EEE and CSE are in the ratio of 6:7:8. In the year 2016 seats were increased by X%, Y% and Z% respectively in the above branches. By this the number of seats in each branch became equal. Then which of the following combination is true?
a)
X = 40 Y = 15 Z = 10
b)
X = 35 Y = 20 Z = 10
c)
X = 40 Y = 25 Z = 5
d)
X = 40 Y = 20 Z = 5
e)
None
|
|
Rhea Reddy answered |
6*140/100 = 7*120/100 = 8*105/100
Shiva is running on a road at the rate of 10 Km/hr. In the same direction a Bus going at a speed of 130 Km/hr passed him. He could see the Bus only for 30 Seconds. Then up to what distance he could see the Bus?- a)1 Km
- b)2 Km
- c)3 Km
- d)4 Km
- e)Cannot be determined
Correct answer is option 'A'. Can you explain this answer?
Shiva is running on a road at the rate of 10 Km/hr. In the same direction a Bus going at a speed of 130 Km/hr passed him. He could see the Bus only for 30 Seconds. Then up to what distance he could see the Bus?
a)
1 Km
b)
2 Km
c)
3 Km
d)
4 Km
e)
Cannot be determined
|
|
Sagar Sharma answered |
Distance Formula
To solve this problem, we need to use the distance formula. The distance formula is given by:
Distance = Speed x Time
Given Information
From the given information, we know the following:
Shiva's speed = 10 km/hr
Bus's speed = 130 km/hr
Time = 30 seconds
Calculating the Distance
To calculate the distance, we need to convert the time from seconds to hours. Since there are 60 seconds in a minute and 60 minutes in an hour, we divide the time by 3600 (60 x 60) to convert it to hours.
Time = 30 seconds ÷ 3600 = 0.00833 hours
Next, we use the distance formula to calculate the distance Shiva could see the bus:
Distance = Speed x Time
Distance = 10 km/hr x 0.00833 hours
Distance = 0.0833 km
Answer
Therefore, Shiva could see the bus up to a distance of 0.0833 km, which is approximately equal to 1 km.
Explanation
When Shiva is running at a speed of 10 km/hr, he can see the bus for a certain amount of time. In this case, the time is given as 30 seconds. To calculate the distance that Shiva could see the bus, we need to use the distance formula. The distance formula states that the distance is equal to the speed multiplied by the time. By substituting the given values into the formula, we can find the distance. After converting the time from seconds to hours, we multiply it by Shiva's speed to get the distance. In this case, the distance is approximately equal to 0.0833 km, which is rounded to 1 km. Therefore, the correct answer is option A - 1 km.
To solve this problem, we need to use the distance formula. The distance formula is given by:
Distance = Speed x Time
Given Information
From the given information, we know the following:
Shiva's speed = 10 km/hr
Bus's speed = 130 km/hr
Time = 30 seconds
Calculating the Distance
To calculate the distance, we need to convert the time from seconds to hours. Since there are 60 seconds in a minute and 60 minutes in an hour, we divide the time by 3600 (60 x 60) to convert it to hours.
Time = 30 seconds ÷ 3600 = 0.00833 hours
Next, we use the distance formula to calculate the distance Shiva could see the bus:
Distance = Speed x Time
Distance = 10 km/hr x 0.00833 hours
Distance = 0.0833 km
Answer
Therefore, Shiva could see the bus up to a distance of 0.0833 km, which is approximately equal to 1 km.
Explanation
When Shiva is running at a speed of 10 km/hr, he can see the bus for a certain amount of time. In this case, the time is given as 30 seconds. To calculate the distance that Shiva could see the bus, we need to use the distance formula. The distance formula states that the distance is equal to the speed multiplied by the time. By substituting the given values into the formula, we can find the distance. After converting the time from seconds to hours, we multiply it by Shiva's speed to get the distance. In this case, the distance is approximately equal to 0.0833 km, which is rounded to 1 km. Therefore, the correct answer is option A - 1 km.
A lift in an Apartment which has 6 floors stops on every floor. If 4 people enter the lift when it was in ground level(ground is not a floor). What is the probability that all will get out on different floors?- a)6!/2!*64
- b)4!/2!*64
- c)6!/4!*64
- d)4!/6!
- e)None
Correct answer is option 'E'. Can you explain this answer?
A lift in an Apartment which has 6 floors stops on every floor. If 4 people enter the lift when it was in ground level(ground is not a floor). What is the probability that all will get out on different floors?
a)
6!/2!*64
b)
4!/2!*64
c)
6!/4!*64
d)
4!/6!
e)
None
|
|
Sagar Sharma answered |
To find the probability that all four people will get out on different floors, we need to consider the number of possible outcomes and the number of favorable outcomes.
Number of possible outcomes:
When each person gets off on a different floor, there are 6 possible choices for the first person, 5 choices for the second person, 4 choices for the third person, and 3 choices for the fourth person. Therefore, the number of possible outcomes is 6 * 5 * 4 * 3 = 360.
Number of favorable outcomes:
Since there are 6 floors and each person needs to get off on a different floor, the first person has 6 choices, the second person has 5 choices (as one floor is already occupied by the first person), the third person has 4 choices, and the fourth person has 3 choices. Therefore, the number of favorable outcomes is 6 * 5 * 4 * 3 = 360.
Probability:
The probability of an event occurring is given by the ratio of the number of favorable outcomes to the number of possible outcomes. In this case, the number of favorable outcomes is equal to the number of possible outcomes. Hence, the probability is 360/360 = 1.
Therefore, the correct answer is option E) None, as the probability of all four people getting out on different floors is 1.
Number of possible outcomes:
When each person gets off on a different floor, there are 6 possible choices for the first person, 5 choices for the second person, 4 choices for the third person, and 3 choices for the fourth person. Therefore, the number of possible outcomes is 6 * 5 * 4 * 3 = 360.
Number of favorable outcomes:
Since there are 6 floors and each person needs to get off on a different floor, the first person has 6 choices, the second person has 5 choices (as one floor is already occupied by the first person), the third person has 4 choices, and the fourth person has 3 choices. Therefore, the number of favorable outcomes is 6 * 5 * 4 * 3 = 360.
Probability:
The probability of an event occurring is given by the ratio of the number of favorable outcomes to the number of possible outcomes. In this case, the number of favorable outcomes is equal to the number of possible outcomes. Hence, the probability is 360/360 = 1.
Therefore, the correct answer is option E) None, as the probability of all four people getting out on different floors is 1.
A man can cross a downstream river with Streamer and Boat in 40 minutes and 72 minutes respectively. If the time of crossing Upstream by streamer is 50% more than Downstream time and the time required by Boat in Upstream is 75% more than time required by it in Downstream. What is the time taken for the man to cross the river downstream by streamer and then return to same place by Boat half way and by streamer the rest of the way?- a)113 minutes
- b)123 minutes
- c)133 minutes
- d)143 minutes
- e)None
Correct answer is option 'C'. Can you explain this answer?
A man can cross a downstream river with Streamer and Boat in 40 minutes and 72 minutes respectively. If the time of crossing Upstream by streamer is 50% more than Downstream time and the time required by Boat in Upstream is 75% more than time required by it in Downstream. What is the time taken for the man to cross the river downstream by streamer and then return to same place by Boat half way and by streamer the rest of the way?
a)
113 minutes
b)
123 minutes
c)
133 minutes
d)
143 minutes
e)
None
|
|
Aarav Sharma answered |
Upstream – streamer – 60 min
Upstream – Boat – 126 min
40+30+63 = 133 minutes
Upstream – Boat – 126 min
40+30+63 = 133 minutes
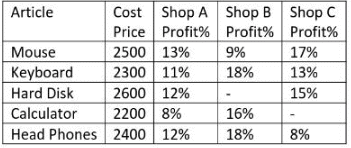 Q. What is the average profit made Shop A, B and C on Mouse?
Q. What is the average profit made Shop A, B and C on Mouse?- a)345
- b)335
- c)325
- d)315
- e)None
Correct answer is option 'C'. Can you explain this answer?
Q.
What is the average profit made Shop A, B and C on Mouse?
a)
345
b)
335
c)
325
d)
315
e)
None
|
|
Vishal Musmade answered |
If we can do total profit =(13+9+17)/3
so it is 13 we multiple this with cost we will get ans
(13/100)*2500=325
so it is 13 we multiple this with cost we will get ans
(13/100)*2500=325
Ravi took a Loan of 4Lakh rupees from a Bank on a condition that he will be charged at 5% p.a. at CI for the first 2 years and at 10% p.a. at CI for the rest of the years. After 2 years he returned 2/3 amount which has to be paid. He returned remaining amount again after 2 years. Then what is the total amount paid by him to Bank?- a)618770
- b)618780
- c)617780
- d)618870
- e)None
Correct answer is option 'D'. Can you explain this answer?
Ravi took a Loan of 4Lakh rupees from a Bank on a condition that he will be charged at 5% p.a. at CI for the first 2 years and at 10% p.a. at CI for the rest of the years. After 2 years he returned 2/3 amount which has to be paid. He returned remaining amount again after 2 years. Then what is the total amount paid by him to Bank?
a)
618770
b)
618780
c)
617780
d)
618870
e)
None
|
|
Kavya Saxena answered |
@5% = 4L*(1+5/100) 2 = 441000
returned 2/3 = 147000
@10% = 147000*(1+10/100) 2 = 177870
Total = 441000+177870 = 618870
returned 2/3 = 147000
@10% = 147000*(1+10/100) 2 = 177870
Total = 441000+177870 = 618870
Study the given table and answer the following questions Q. If the difference between the Profits made by Shop A and Shop B on Mouse is equal to the Profit earned by Shop C on Calculator then his Profit percent is?
Q. If the difference between the Profits made by Shop A and Shop B on Mouse is equal to the Profit earned by Shop C on Calculator then his Profit percent is?- a)50/13%
- b)49/11%
- c)50/11%
- d)50/23%
- e)Cannot be determined
Correct answer is option 'C'. Can you explain this answer?
Study the given table and answer the following questions
Q.
If the difference between the Profits made by Shop A and Shop B on Mouse is equal to the Profit earned by Shop C on Calculator then his Profit percent is?
a)
50/13%
b)
49/11%
c)
50/11%
d)
50/23%
e)
Cannot be determined
|
|
Aisha Gupta answered |
2500*(13-9)/100 = Rs 100
2300 = 2200(100+x)/100
X = 50/11%
2300 = 2200(100+x)/100
X = 50/11%
Find out the wrong number in the following series8,19,188,573,1154,1159- a)19
- b)188
- c)573
- d)1154
- e)1159
Correct answer is option 'A'. Can you explain this answer?
Find out the wrong number in the following series
8,19,188,573,1154,1159
a)
19
b)
188
c)
573
d)
1154
e)
1159
|
|
Faizan Khan answered |
(8+1)*5 = 45
(45+2)*4 = 188
(188+3)*3 = 573
(573+4)*2 = 1154
(1154+5)*1 = 1159
(45+2)*4 = 188
(188+3)*3 = 573
(573+4)*2 = 1154
(1154+5)*1 = 1159

 Note: Total Population = Men + Women + Children.Q. If the ratio of total number of Job holders in the year 2012 to total number of Job holders in the year 2014 is 1:1, then total population in the year 2014 is?
Note: Total Population = Men + Women + Children.Q. If the ratio of total number of Job holders in the year 2012 to total number of Job holders in the year 2014 is 1:1, then total population in the year 2014 is?- a)9001
- b)9101
- c)9201
- d)9301
- e)Cannot be determined
Correct answer is option 'C'. Can you explain this answer?
Note: Total Population = Men + Women + Children.
Q.
If the ratio of total number of Job holders in the year 2012 to total number of Job holders in the year 2014 is 1:1, then total population in the year 2014 is?
a)
9001
b)
9101
c)
9201
d)
9301
e)
Cannot be determined
|
|
Aarav Sharma answered |
4300*47+3400*32 = X*46+3500*31
X= 4400
Total population = 4400+3500+1301 = 9201
X= 4400
Total population = 4400+3500+1301 = 9201
Shopkeeper A bought a 10 chocolate packs having 9 chocolates in each pack at the rate Rs.1.5 per chocolate. Shopkeeper B bought 11 chocolate packs having 8 chocolates in each pack at the rate of Rs. 2 per chocolate. Shopkeeper A made 20% profit by selling all chocolates. Shopkeeper B is chocoholic he ate some chocolates and sold rest of the he chocolates at the same Selling Price as of A. Then how many chocolates did shopkeeper B eat?- a)5
- b)6
- c)7
- d)8
- e)None
Correct answer is option 'C'. Can you explain this answer?
Shopkeeper A bought a 10 chocolate packs having 9 chocolates in each pack at the rate Rs.1.5 per chocolate. Shopkeeper B bought 11 chocolate packs having 8 chocolates in each pack at the rate of Rs. 2 per chocolate. Shopkeeper A made 20% profit by selling all chocolates. Shopkeeper B is chocoholic he ate some chocolates and sold rest of the he chocolates at the same Selling Price as of A. Then how many chocolates did shopkeeper B eat?
a)
5
b)
6
c)
7
d)
8
e)
None
|
|
Alok Verma answered |
Shop A
10*9*1.5 = 135
135*120/100 =162
Shop B
11*8*2 = 176
162= 176-2x
x =7
10*9*1.5 = 135
135*120/100 =162
Shop B
11*8*2 = 176
162= 176-2x
x =7
Sumit lent a part of Rs. 6000 to Ramya at 6% SI. Rest to Anita at 5% SI. After 3 years he got an amount of Rs 6984 in total. Then what is the amount paid by Anita in total?- a)Rs.2800
- b)Rs.3304
- c)Rs.3200
- d)Rs.3680
- e)Cannot be determined
Correct answer is option 'D'. Can you explain this answer?
Sumit lent a part of Rs. 6000 to Ramya at 6% SI. Rest to Anita at 5% SI. After 3 years he got an amount of Rs 6984 in total. Then what is the amount paid by Anita in total?
a)
Rs.2800
b)
Rs.3304
c)
Rs.3200
d)
Rs.3680
e)
Cannot be determined
|
|
Faizan Khan answered |
x*18+(6000-x)*15 = 98400
x = 2800
Anita = 3200+3200*5*3/100 = 3680
x = 2800
Anita = 3200+3200*5*3/100 = 3680
A building contractor takes contract to do a work in 30 days by 40 men. In the first 10 days 10 men were absent. In the second 10 days all men were present. Now how many more men he need to employ so that work is finished in time?- a)10
- b)20
- c)30
- d)40
- e)None
Correct answer is option 'A'. Can you explain this answer?
A building contractor takes contract to do a work in 30 days by 40 men. In the first 10 days 10 men were absent. In the second 10 days all men were present. Now how many more men he need to employ so that work is finished in time?
a)
10
b)
20
c)
30
d)
40
e)
None
|
|
Sagar Sharma answered |
Understanding the Problem
A contractor has to complete a project in 30 days using 40 men. The work is divided into three segments over these 30 days.
Work Distribution
- Total Work: The total work can be calculated as "man-days" which is 40 men * 30 days = 1200 man-days.
Work Done in the First 10 Days
- Men Present: During the first 10 days, 10 men were absent, leaving 30 men available.
- Work Done:
- Work done in 10 days = 30 men * 10 days = 300 man-days.
Work Done in the Second 10 Days
- Men Present: All 40 men were present in the next 10 days.
- Work Done:
- Work done in the second 10 days = 40 men * 10 days = 400 man-days.
Total Work Completed
- Total Work After 20 Days:
- Total work done in 20 days = 300 man-days + 400 man-days = 700 man-days.
Remaining Work
- Remaining Work:
- Remaining work = Total work - Work done = 1200 man-days - 700 man-days = 500 man-days.
Time Remaining
- Days Left:
- Days remaining = 30 days - 20 days = 10 days.
Calculating Additional Men Needed
- Men Needed:
- To complete 500 man-days in 10 days, the required number of men = Remaining work / Days remaining = 500 man-days / 10 days = 50 men.
- Additional Men Required:
- Since there are already 40 men, additional men needed = 50 men - 40 men = 10 men.
Conclusion
The contractor needs to employ 10 more men to finish the work on time. Thus, the correct answer is option 'A'.
A contractor has to complete a project in 30 days using 40 men. The work is divided into three segments over these 30 days.
Work Distribution
- Total Work: The total work can be calculated as "man-days" which is 40 men * 30 days = 1200 man-days.
Work Done in the First 10 Days
- Men Present: During the first 10 days, 10 men were absent, leaving 30 men available.
- Work Done:
- Work done in 10 days = 30 men * 10 days = 300 man-days.
Work Done in the Second 10 Days
- Men Present: All 40 men were present in the next 10 days.
- Work Done:
- Work done in the second 10 days = 40 men * 10 days = 400 man-days.
Total Work Completed
- Total Work After 20 Days:
- Total work done in 20 days = 300 man-days + 400 man-days = 700 man-days.
Remaining Work
- Remaining Work:
- Remaining work = Total work - Work done = 1200 man-days - 700 man-days = 500 man-days.
Time Remaining
- Days Left:
- Days remaining = 30 days - 20 days = 10 days.
Calculating Additional Men Needed
- Men Needed:
- To complete 500 man-days in 10 days, the required number of men = Remaining work / Days remaining = 500 man-days / 10 days = 50 men.
- Additional Men Required:
- Since there are already 40 men, additional men needed = 50 men - 40 men = 10 men.
Conclusion
The contractor needs to employ 10 more men to finish the work on time. Thus, the correct answer is option 'A'.
Raju and Ramu can complete a work alone in 24 hours and 30 hours respectively, working 10 hours a day. Every day there are two shits- Morning and Night Shift for 6 and 4 hours respectively. On first day Raju works in Morning shift while Ramu works in Night shift. Next day Ramu works in Morning shift while Raju works in Night shift. They repeat the cycle until the work is completed. Then how many hours does Raju worked in total?- a)130
- b)136
- c)140
- d)146
- e)Cannot be determined
Correct answer is option 'B'. Can you explain this answer?
Raju and Ramu can complete a work alone in 24 hours and 30 hours respectively, working 10 hours a day. Every day there are two shits- Morning and Night Shift for 6 and 4 hours respectively. On first day Raju works in Morning shift while Ramu works in Night shift. Next day Ramu works in Morning shift while Raju works in Night shift. They repeat the cycle until the work is completed. Then how many hours does Raju worked in total?
a)
130
b)
136
c)
140
d)
146
e)
Cannot be determined
|
|
Nikita Singh answered |
Day 1 : 6/240+4/300
Day 2 : 4/240 + 6/300
2 days work : 10/240 + 10/300 = 9/120
2*13 days work = 117/120
remaining work = 3/120
Now Raju’s turn in morning shift
3/120*240/6 =1(completes in his shift)
Total Raju Hour’s = 13*6+13*4+6 =136
Day 2 : 4/240 + 6/300
2 days work : 10/240 + 10/300 = 9/120
2*13 days work = 117/120
remaining work = 3/120
Now Raju’s turn in morning shift
3/120*240/6 =1(completes in his shift)
Total Raju Hour’s = 13*6+13*4+6 =136
(1421/47) ÷ (49/828) *(1645/23) = ?3 + 603- a)33
- b)34
- c)35
- d)36
- e)37
Correct answer is option 'A'. Can you explain this answer?
(1421/47) ÷ (49/828) *(1645/23) = ?3 + 603
a)
33
b)
34
c)
35
d)
36
e)
37

|
Ishani Rane answered |
29*36*35 = 36540 = ? 3 +603
? =33
Find out the wrong number in the following series22,10,8,11,20,49,96- a)8
- b)11
- c)49
- d)96
- e)20
Correct answer is option 'D'. Can you explain this answer?
Find out the wrong number in the following series
22,10,8,11,20,49,96
a)
8
b)
11
c)
49
d)
96
e)
20
|
|
Anaya Patel answered |
22*0.5 – 1 =10
10*1 – 2 = 8
8*1.5 – 1 = 11
11*2 – 2 = 20
20*2.5 – 1 = 49
49*3 – 2 = 145
10*1 – 2 = 8
8*1.5 – 1 = 11
11*2 – 2 = 20
20*2.5 – 1 = 49
49*3 – 2 = 145
In the year 2016 the average number of people visited Goa per day is 73. In the next year number of visitors increased by 657. Then average number of people visited Goa in the year 2017 is ?- a)73
- b)74
- c)75
- d)76
- e)Cannot be determined
Correct answer is option 'C'. Can you explain this answer?
In the year 2016 the average number of people visited Goa per day is 73. In the next year number of visitors increased by 657. Then average number of people visited Goa in the year 2017 is ?
a)
73
b)
74
c)
75
d)
76
e)
Cannot be determined
|
|
Preeti Khanna answered |
x/366 =73
x = 26718
In 2017 = 26718+657 = 27375
average = 27375/365 = 75
x = 26718
In 2017 = 26718+657 = 27375
average = 27375/365 = 75
Sravan has to row from place A to place B and back in 6 hours which is at a certain distance. Due to bad light, he couldn’t recognize Place B and rowed 60 Km further. Then he realized and started return back to Place A. Due to this he travelled for 2 more hours than the original journey. Ratio of the speed of Boat to the stream is 2:1. Then what is entire distance covered by him?.- a)240 Km
- b)300 Km
- c)360 Km
- d)480 Km
- e)Cannot be determined
Correct answer is option 'D'. Can you explain this answer?
Sravan has to row from place A to place B and back in 6 hours which is at a certain distance. Due to bad light, he couldn’t recognize Place B and rowed 60 Km further. Then he realized and started return back to Place A. Due to this he travelled for 2 more hours than the original journey. Ratio of the speed of Boat to the stream is 2:1. Then what is entire distance covered by him?.
a)
240 Km
b)
300 Km
c)
360 Km
d)
480 Km
e)
Cannot be determined
|
|
Anaya Patel answered |
6 = D(1/3x+1/x)
2= 60(1/3x+1/x)
x = 40
D =180
Total distance travelled = (180+60)*2 = 480
2= 60(1/3x+1/x)
x = 40
D =180
Total distance travelled = (180+60)*2 = 480
I. 2X² – 15√2X + 56 = 0II. 2Y² – 17√2Y + 72= 0- a)X > Y
- b)X < Y
- c)X ≥ Y
- d)X ≤ Y
- e)X = Y or relationship cannot be established
Correct answer is option 'D'. Can you explain this answer?
I. 2X² – 15√2X + 56 = 0
II. 2Y² – 17√2Y + 72= 0
a)
X > Y
b)
X < Y
c)
X ≥ Y
d)
X ≤ Y
e)
X = Y or relationship cannot be established
|
|
Sagar Sharma answered |
Understanding the Equations
We have two quadratic equations to analyze:
- I. 2X² – 15√2X + 56 = 0
- II. 2Y² – 17√2Y + 72 = 0
Step 1: Solving for X
To find the roots (X values) of equation I:
- The coefficients are: a = 2, b = -15√2, c = 56.
- Using the quadratic formula, X = [ -b ± √(b² - 4ac) ] / 2a.
Calculating the discriminant (b² - 4ac):
- b² = (-15√2)² = 450
- 4ac = 4 * 2 * 56 = 448
- Discriminant = 450 - 448 = 2 (positive, hence two real roots)
Now, compute the roots:
- X1 = [15√2 + √2] / 4 = (15 + 1)√2 / 4 = 16√2 / 4 = 4√2
- X2 = [15√2 - √2] / 4 = (15 - 1)√2 / 4 = 14√2 / 4 = 3.5√2
Step 2: Solving for Y
Now for equation II:
- The coefficients are: a = 2, b = -17√2, c = 72.
- Using the quadratic formula again.
Calculating the discriminant:
- b² = (-17√2)² = 578
- 4ac = 4 * 2 * 72 = 576
- Discriminant = 578 - 576 = 2 (positive, two real roots)
Now, compute the roots:
- Y1 = [17√2 + √2] / 4 = (17 + 1)√2 / 4 = 18√2 / 4 = 4.5√2
- Y2 = [17√2 - √2] / 4 = (17 - 1)√2 / 4 = 16√2 / 4 = 4√2
Comparing X and Y
From the calculations:
- X values: 4√2 and 3.5√2
- Y values: 4.5√2 and 4√2
Conclusion
- The maximum value of X (4√2) is equal to the minimum value of Y (4√2).
- Since the values of X can be less than or equal to Y, the correct answer is option 'D': X ≤ Y.
We have two quadratic equations to analyze:
- I. 2X² – 15√2X + 56 = 0
- II. 2Y² – 17√2Y + 72 = 0
Step 1: Solving for X
To find the roots (X values) of equation I:
- The coefficients are: a = 2, b = -15√2, c = 56.
- Using the quadratic formula, X = [ -b ± √(b² - 4ac) ] / 2a.
Calculating the discriminant (b² - 4ac):
- b² = (-15√2)² = 450
- 4ac = 4 * 2 * 56 = 448
- Discriminant = 450 - 448 = 2 (positive, hence two real roots)
Now, compute the roots:
- X1 = [15√2 + √2] / 4 = (15 + 1)√2 / 4 = 16√2 / 4 = 4√2
- X2 = [15√2 - √2] / 4 = (15 - 1)√2 / 4 = 14√2 / 4 = 3.5√2
Step 2: Solving for Y
Now for equation II:
- The coefficients are: a = 2, b = -17√2, c = 72.
- Using the quadratic formula again.
Calculating the discriminant:
- b² = (-17√2)² = 578
- 4ac = 4 * 2 * 72 = 576
- Discriminant = 578 - 576 = 2 (positive, two real roots)
Now, compute the roots:
- Y1 = [17√2 + √2] / 4 = (17 + 1)√2 / 4 = 18√2 / 4 = 4.5√2
- Y2 = [17√2 - √2] / 4 = (17 - 1)√2 / 4 = 16√2 / 4 = 4√2
Comparing X and Y
From the calculations:
- X values: 4√2 and 3.5√2
- Y values: 4.5√2 and 4√2
Conclusion
- The maximum value of X (4√2) is equal to the minimum value of Y (4√2).
- Since the values of X can be less than or equal to Y, the correct answer is option 'D': X ≤ Y.
Ravi, Ramu, Raju invested in the ratio of 5:6:7 respectively. At the end of the business, they received the profit in the ratio of 10:8:7.Quantity I: Time period for which Ravi invested?
Quantity II: Time period for which Ramu invested?
Quantity III: Time period for which Raju invested?- a)Q1>Q2>Q3
- b)Q1>Q3>Q2
- c)Q2>Q3>Q1
- d)Q1=Q2=Q3
- e)Relationship cannot be established
Correct answer is option 'A'. Can you explain this answer?
Ravi, Ramu, Raju invested in the ratio of 5:6:7 respectively. At the end of the business, they received the profit in the ratio of 10:8:7.
Quantity I: Time period for which Ravi invested?
Quantity II: Time period for which Ramu invested?
Quantity III: Time period for which Raju invested?
Quantity II: Time period for which Ramu invested?
Quantity III: Time period for which Raju invested?
a)
Q1>Q2>Q3
b)
Q1>Q3>Q2
c)
Q2>Q3>Q1
d)
Q1=Q2=Q3
e)
Relationship cannot be established
|
|
Anaya Patel answered |
let times be t1,t2, and t3
5t1/6t2 = 10/8
t1:t2 = 3:2
similarly t2:t3 =4:3
t1:t2:t3 = 6:4:3
5t1/6t2 = 10/8
t1:t2 = 3:2
similarly t2:t3 =4:3
t1:t2:t3 = 6:4:3
 Q. If the total profit made by Shop A, B and C on Hard Disk is Rs.988 then what is the profit of B on Hard Disk?
Q. If the total profit made by Shop A, B and C on Hard Disk is Rs.988 then what is the profit of B on Hard Disk?- a)276
- b)286
- c)296
- d)216
- e)None
Correct answer is option 'B'. Can you explain this answer?
Q.
If the total profit made by Shop A, B and C on Hard Disk is Rs.988 then what is the profit of B on Hard Disk?
a)
276
b)
286
c)
296
d)
216
e)
None
|
|
Preeti Khanna answered |
26*(12+x+15) = 988
X = 11%
Profit = 26*11 = 286
X = 11%
Profit = 26*11 = 286
Find out the wrong number in the following series15,17,25,65,145,295- a)17
- b)25
- c)65
- d)145
- e)295
Correct answer is option 'B'. Can you explain this answer?
Find out the wrong number in the following series
15,17,25,65,145,295
a)
17
b)
25
c)
65
d)
145
e)
295
|
|
Preeti Khanna answered |
15+1²+1³ = 17
17+2²+2³ = 29
29+3²+3³ = 65
65+4²+4³ = 145
145+5²+5³ = 295
17+2²+2³ = 29
29+3²+3³ = 65
65+4²+4³ = 145
145+5²+5³ = 295
Direction (Q. 1-5) In the following questions two equations numbered I & II are given. You have to solve both equations and mark one of the option given belowQ. I. 242X² + 88X + 6 = 0
II. 363Y² + 165Y + 12 =0- a)X > Y
- b)X <Y
- c)X ≥ Y
- d)X ≤ Y
- e)X = Y or relationship cannot be established
Correct answer is option 'E'. Can you explain this answer?
Direction (Q. 1-5) In the following questions two equations numbered I & II are given. You have to solve both equations and mark one of the option given below
Q.
I. 242X² + 88X + 6 = 0
II. 363Y² + 165Y + 12 =0
II. 363Y² + 165Y + 12 =0
a)
X > Y
b)
X <Y
c)
X ≥ Y
d)
X ≤ Y
e)
X = Y or relationship cannot be established
|
|
Anaya Patel answered |
X = -3/11, -1/11
Y = -4/11, -1/11
Y = -4/11, -1/11
I. 3X + 4Y = 64II. 2X + 3Y = 56- a)X > Y
- b)X < Y
- c)X ≥ Y
- d)X ≤ Y
- e)X = Y or relationship cannot be established
Correct answer is option 'B'. Can you explain this answer?
I. 3X + 4Y = 64
II. 2X + 3Y = 56
a)
X > Y
b)
X < Y
c)
X ≥ Y
d)
X ≤ Y
e)
X = Y or relationship cannot be established
|
|
Sagar Sharma answered |
Given Equations:
I. 3X + 4Y = 64
II. 2X + 3Y = 56
Explanation:
Step 1: Solving the Equations
To find the relationship between X and Y, we need to solve the given equations simultaneously.
Multiplying Equation I by 2 and Equation II by 3:
6X + 8Y = 128
6X + 9Y = 168
Subtracting Equation I from Equation II:
Y = 40
Substituting Y = 40 in Equation I:
3X + 4(40) = 64
3X + 160 = 64
3X = -96
X = -32
Step 2: Comparing X and Y
X = -32 and Y = 40
Since X is less than Y (X < y),="" the="" correct="" answer="" is="" option="" b)="" x="" />< />
Therefore, the relationship between X and Y is that X is less than Y in this scenario.
I. 3X + 4Y = 64
II. 2X + 3Y = 56
Explanation:
Step 1: Solving the Equations
To find the relationship between X and Y, we need to solve the given equations simultaneously.
Multiplying Equation I by 2 and Equation II by 3:
6X + 8Y = 128
6X + 9Y = 168
Subtracting Equation I from Equation II:
Y = 40
Substituting Y = 40 in Equation I:
3X + 4(40) = 64
3X + 160 = 64
3X = -96
X = -32
Step 2: Comparing X and Y
X = -32 and Y = 40
Since X is less than Y (X < y),="" the="" correct="" answer="" is="" option="" b)="" x="" />< />
Therefore, the relationship between X and Y is that X is less than Y in this scenario.
Ramesh wishes to fence a rectangular farm of 2000m 2 area in which length is greater than breadth. He used 130mts of wire to fence the farm on three sides which is the least length of wire which can be utilized by him. The cost of 1 m wire is Rs.3 then how much difference would be there if he fences fours sides instead of three sides?- a)Rs. 130
- b)Rs. 150
- c)Rs. 180
- d)Rs. 200
- e)None
Correct answer is option 'B'. Can you explain this answer?
Ramesh wishes to fence a rectangular farm of 2000m 2 area in which length is greater than breadth. He used 130mts of wire to fence the farm on three sides which is the least length of wire which can be utilized by him. The cost of 1 m wire is Rs.3 then how much difference would be there if he fences fours sides instead of three sides?
a)
Rs. 130
b)
Rs. 150
c)
Rs. 180
d)
Rs. 200
e)
None
|
|
Anaya Patel answered |
l*b = 2000
2b+l = 130
l = 50 b= 40
cost of fencing three sides = 130*3 = 390
cost of fencing four sides = 180*3 = 540
2b+l = 130
l = 50 b= 40
cost of fencing three sides = 130*3 = 390
cost of fencing four sides = 180*3 = 540
Parthiv’s wife age is 24 and his Son age is 12 as on today. On same day Partiv invented a Time Machine through which he travelled to ancient time. He stayed in ancient time for 6 Years then he returned back. But by Surprise, there is no change in Parthiv’s age after his return. If the difference between the average age of the family before and after is only 4 then Parthiv’s age is?- a)33
- b)39
- c)40
- d)41
- e)Cannot be determined
Correct answer is option 'E'. Can you explain this answer?
Parthiv’s wife age is 24 and his Son age is 12 as on today. On same day Partiv invented a Time Machine through which he travelled to ancient time. He stayed in ancient time for 6 Years then he returned back. But by Surprise, there is no change in Parthiv’s age after his return. If the difference between the average age of the family before and after is only 4 then Parthiv’s age is?
a)
33
b)
39
c)
40
d)
41
e)
Cannot be determined
|
|
Sagar Sharma answered |
Understanding the Family's Age Before Time Travel
- Parthiv's wife's age: 24 years
- Son's age: 12 years
- Parthiv's age: Let’s denote it as P.
Calculating the Average Age Before Time Travel
- Total age before time travel = P + 24 + 12 = P + 36
- Number of family members = 3
- Average age before time travel = (P + 36) / 3
Time Travel Duration
- Time spent in ancient time: 6 years
- After returning, Parthiv's age remains P, while his wife and son age 6 years:
- Wife's new age = 24 + 6 = 30
- Son's new age = 12 + 6 = 18
Calculating the Average Age After Time Travel
- Total age after time travel = P + 30 + 18 = P + 48
- Average age after time travel = (P + 48) / 3
Difference in Average Ages
- Given that the difference in averages is 4:
- [(P + 48) / 3] - [(P + 36) / 3] = 4
- Simplifying gives:
- (P + 48 - P - 36) / 3 = 4
- 12 / 3 = 4 (which holds true)
Conclusion: Age of Parthiv
The equation does not provide a specific value for P, meaning it could be any value that satisfies the overall condition of age difference. Thus, the exact age of Parthiv cannot be determined based solely on the information provided, leading to the answer being option 'E' (Cannot be determined).
- Parthiv's wife's age: 24 years
- Son's age: 12 years
- Parthiv's age: Let’s denote it as P.
Calculating the Average Age Before Time Travel
- Total age before time travel = P + 24 + 12 = P + 36
- Number of family members = 3
- Average age before time travel = (P + 36) / 3
Time Travel Duration
- Time spent in ancient time: 6 years
- After returning, Parthiv's age remains P, while his wife and son age 6 years:
- Wife's new age = 24 + 6 = 30
- Son's new age = 12 + 6 = 18
Calculating the Average Age After Time Travel
- Total age after time travel = P + 30 + 18 = P + 48
- Average age after time travel = (P + 48) / 3
Difference in Average Ages
- Given that the difference in averages is 4:
- [(P + 48) / 3] - [(P + 36) / 3] = 4
- Simplifying gives:
- (P + 48 - P - 36) / 3 = 4
- 12 / 3 = 4 (which holds true)
Conclusion: Age of Parthiv
The equation does not provide a specific value for P, meaning it could be any value that satisfies the overall condition of age difference. Thus, the exact age of Parthiv cannot be determined based solely on the information provided, leading to the answer being option 'E' (Cannot be determined).
When Suresh was born, his father age was 27 years older than his Brother and his Mother was 24 years older than his Sister. If his Brother is 2 year is elder than his Sister.Then his Father is how many years older than his Mother after 6 years?- a)4
- b)5
- c)6
- d)7
- e)Cannot be determined
Correct answer is option 'B'. Can you explain this answer?
When Suresh was born, his father age was 27 years older than his Brother and his Mother was 24 years older than his Sister. If his Brother is 2 year is elder than his Sister.Then his Father is how many years older than his Mother after 6 years?
a)
4
b)
5
c)
6
d)
7
e)
Cannot be determined
|
|
Alok Verma answered |
Sister age = x
Father age = x+29
Mother age = x+24
29-24 = 5
Father age = x+29
Mother age = x+24
29-24 = 5
What is the area of the rectangle?I. The perimeter of rectangle is 156 cm
II. The diagonal of rectangle is √3060 cm- a)The data in statement I alone are sufficient to answer the question, while data in statement II are not sufficient to answer the question
- b)The data in statement II alone are sufficient to answer the question, while data in statement I are not sufficient to answer the question
- c)The data either in Statement I alone or Statement II alone are sufficient to answer the question
- d)The data given in Both Statements I & II are not sufficient to answer the question
- e)The data given in both statements I & II together are necessary to answer the question
Correct answer is option 'E'. Can you explain this answer?
What is the area of the rectangle?
I. The perimeter of rectangle is 156 cm
II. The diagonal of rectangle is √3060 cm
II. The diagonal of rectangle is √3060 cm
a)
The data in statement I alone are sufficient to answer the question, while data in statement II are not sufficient to answer the question
b)
The data in statement II alone are sufficient to answer the question, while data in statement I are not sufficient to answer the question
c)
The data either in Statement I alone or Statement II alone are sufficient to answer the question
d)
The data given in Both Statements I & II are not sufficient to answer the question
e)
The data given in both statements I & II together are necessary to answer the question
|
|
Alok Verma answered |
l+b = 78
l² + b² = 3060
l² + b² = 3060
5 x 11111 + 52 x 1111 + 53 x 111 + 54 x 11 + 55 x 1 = ?- a)107205
- b)107225
- c)117205
- d)117225
- e)None
Correct answer is option 'A'. Can you explain this answer?
5 x 11111 + 52 x 1111 + 53 x 111 + 54 x 11 + 55 x 1 = ?
a)
107205
b)
107225
c)
117205
d)
117225
e)
None
|
|
Nikita Singh answered |
55555+27775+13875+6875+3125=107205
2,14,72,252,568,?- a)668
- b)922
- c)1024
- d)1136
- e)None
Correct answer is option 'A'. Can you explain this answer?
2,14,72,252,568,?
a)
668
b)
922
c)
1024
d)
1136
e)
None
|
|
Preeti Khanna answered |
2*5+2² = 14
14*4+4² = 72
72*3+6² = 252
252*2+8² = 568
568*1+10² = 668
14*4+4² = 72
72*3+6² = 252
252*2+8² = 568
568*1+10² = 668

 Q. If the number of candidates qualified in TCS is 7319 more than the number of candidates qualified in CTS then the number of Male candidates qualified is how much more than the number of Female candidates in CTS?
Q. If the number of candidates qualified in TCS is 7319 more than the number of candidates qualified in CTS then the number of Male candidates qualified is how much more than the number of Female candidates in CTS?- a)7157
- b)7257
- c)7657
- d)7967
- e)Cannot be determined
Correct answer is option 'C'. Can you explain this answer?
Q.
If the number of candidates qualified in TCS is 7319 more than the number of candidates qualified in CTS then the number of Male candidates qualified is how much more than the number of Female candidates in CTS?
a)
7157
b)
7257
c)
7657
d)
7967
e)
Cannot be determined
|
|
Yash Patel answered |
TCS = 312000*98/100*65/100 = 637*312
CTS = 325000*x/100*62/100 =
TCS – CTS = 73190 = 312000* 98/100* 65/100 – 325000* x/100* 62/100
Then x = 95%
CTS (Males – Females) : 325000*95/100*62/100*(13-12/25) = 7657
CTS = 325000*x/100*62/100 =
TCS – CTS = 73190 = 312000* 98/100* 65/100 – 325000* x/100* 62/100
Then x = 95%
CTS (Males – Females) : 325000*95/100*62/100*(13-12/25) = 7657
What is the percentage of Illiterates in the Town?I. A Town having Three Localities X, Y and Z have population in the ratio of 10:11:12
II. In locality X, 70% are literate, in locality Y, 20% are illiterate, in locality Z, 60% are literate- a)The data in statement I alone are sufficient to answer the question, while data in statement II are not sufficient to answer the question
- b)The data in statement II alone are sufficient to answer the question, while data in statement I are not sufficient to answer the question
- c)The data either in Statement I alone or Statement II alone are sufficient to answer the question
- d)The data given in Both Statements I & II are not sufficient to answer the question
- e)The data given in both statements I & II together are necessary to answer the question
Correct answer is option 'E'. Can you explain this answer?
What is the percentage of Illiterates in the Town?
I. A Town having Three Localities X, Y and Z have population in the ratio of 10:11:12
II. In locality X, 70% are literate, in locality Y, 20% are illiterate, in locality Z, 60% are literate
II. In locality X, 70% are literate, in locality Y, 20% are illiterate, in locality Z, 60% are literate
a)
The data in statement I alone are sufficient to answer the question, while data in statement II are not sufficient to answer the question
b)
The data in statement II alone are sufficient to answer the question, while data in statement I are not sufficient to answer the question
c)
The data either in Statement I alone or Statement II alone are sufficient to answer the question
d)
The data given in Both Statements I & II are not sufficient to answer the question
e)
The data given in both statements I & II together are necessary to answer the question
|
|
Sagar Sharma answered |
And II together are not sufficient to answer the question
From a container of Milk, a thief has stolen 16 litres of Milk and replaced it with same quantity of water. He repeated the same process again two more times. Then ratio of Milk and Water is 3375:1538. Then what is the initial amount of Milk in the container?- a)120 Litre
- b)136 Litre
- c)142 Litre
- d)154 Litre
- e)None
Correct answer is option 'B'. Can you explain this answer?
From a container of Milk, a thief has stolen 16 litres of Milk and replaced it with same quantity of water. He repeated the same process again two more times. Then ratio of Milk and Water is 3375:1538. Then what is the initial amount of Milk in the container?
a)
120 Litre
b)
136 Litre
c)
142 Litre
d)
154 Litre
e)
None
|
|
Anaya Patel answered |
3375x = 4913x(1-16/y) 3
15/17 = 1-16/y
y = 136
15/17 = 1-16/y
y = 136
I.2X² – (4+√14)X +√56 = 0II.10Y² – (18+5√14)Y + 9√14 =0- a)X > Y
- b)X <Y
- c)X ≥ Y
- d)X ≤ Y
- e)X = Y or relationship cannot be established
Correct answer is option 'C'. Can you explain this answer?
I.2X² – (4+√14)X +√56 = 0
II.10Y² – (18+5√14)Y + 9√14 =0
a)
X > Y
b)
X <Y
c)
X ≥ Y
d)
X ≤ Y
e)
X = Y or relationship cannot be established
|
|
Sagar Sharma answered |
Understanding the Equations
The given equations are quadratic equations in X and Y. We need to analyze each equation to determine the relationship between their roots.
Equation I: 2X² - (4 + √14)X + √56 = 0
- For this quadratic equation in X, we can find the roots using the quadratic formula:
X = [-(b) ± √(b² - 4ac)] / (2a)
Here, a = 2, b = -(4 + √14), and c = √56.
- The roots' relationship will depend on the discriminant (D):
D = b² - 4ac.
If D > 0, there are two distinct real roots; if D = 0, one real root; and if D < 0,="" no="" real="" />
Equation II: 10Y² - (18 + 5√14)Y + 9√14 = 0
- Similarly, for this quadratic in Y, use the quadratic formula:
Y = [-(b) ± √(b² - 4ac)] / (2a)
Here, a = 10, b = -(18 + 5√14), and c = 9√14.
- Again, compute the discriminant (D):
D = b² - 4ac, with the same implications for the roots.
Comparing the Roots
- Both equations represent parabolas, and their roots can be numerical values based on the discriminants.
- If we compute the discriminants and find them to be equal, or if they yield roots that are numerically the same, we can establish that X = Y.
- If the discriminants are positive but yield different values, we would need to compare the roots directly to ascertain if X > Y or X < />
Conclusion
Given that the correct answer is 'C', it implies that after analyzing the roots from both equations, they can be equal or cannot be distinctly separated. Thus, X can be greater than or equal to Y depending on the specific values computed from the equations.
The given equations are quadratic equations in X and Y. We need to analyze each equation to determine the relationship between their roots.
Equation I: 2X² - (4 + √14)X + √56 = 0
- For this quadratic equation in X, we can find the roots using the quadratic formula:
X = [-(b) ± √(b² - 4ac)] / (2a)
Here, a = 2, b = -(4 + √14), and c = √56.
- The roots' relationship will depend on the discriminant (D):
D = b² - 4ac.
If D > 0, there are two distinct real roots; if D = 0, one real root; and if D < 0,="" no="" real="" />
Equation II: 10Y² - (18 + 5√14)Y + 9√14 = 0
- Similarly, for this quadratic in Y, use the quadratic formula:
Y = [-(b) ± √(b² - 4ac)] / (2a)
Here, a = 10, b = -(18 + 5√14), and c = 9√14.
- Again, compute the discriminant (D):
D = b² - 4ac, with the same implications for the roots.
Comparing the Roots
- Both equations represent parabolas, and their roots can be numerical values based on the discriminants.
- If we compute the discriminants and find them to be equal, or if they yield roots that are numerically the same, we can establish that X = Y.
- If the discriminants are positive but yield different values, we would need to compare the roots directly to ascertain if X > Y or X < />
Conclusion
Given that the correct answer is 'C', it implies that after analyzing the roots from both equations, they can be equal or cannot be distinctly separated. Thus, X can be greater than or equal to Y depending on the specific values computed from the equations.

 Q. In TCS females Qualified forms approximately what percent of Qualified Males if no of Males Qualified is 114660?
Q. In TCS females Qualified forms approximately what percent of Qualified Males if no of Males Qualified is 114660?- a)67.77%
- b)71.11%
- c)73.33%
- d)76.66%
- e)Cannot be determined
Correct answer is option 'C'. Can you explain this answer?
Q.
In TCS females Qualified forms approximately what percent of Qualified Males if no of Males Qualified is 114660?
a)
67.77%
b)
71.11%
c)
73.33%
d)
76.66%
e)
Cannot be determined
|
|
Preeti Khanna answered |
312000*98/100*65/100*(15/15+x) = 114660
X= 11
% = 11/15*100 = 73.33%
X= 11
% = 11/15*100 = 73.33%
Chapter doubts & questions for Exam Based Questions - NABARD Grade A & Grade B Preparation 2025 is part of Bank Exams exam preparation. The chapters have been prepared according to the Bank Exams exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Bank Exams 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Exam Based Questions - NABARD Grade A & Grade B Preparation in English & Hindi are available as part of Bank Exams exam.
Download more important topics, notes, lectures and mock test series for Bank Exams Exam by signing up for free.
NABARD Grade A & Grade B Preparation
886 videos|1436 docs|437 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup










