All Exams >
GMAT >
Quantitative for GMAT >
All Questions
All questions of Time, Speed and Distance for GMAT Exam
Can you explain the answer of this question below:Alice, while driving to her workplace completes an initial distance of 50 miles in 2 hours and remaining 60 miles in 3 hours. What is the average speed in miles per hour for her entire journey?
- A:
22
- B:
22.5
- C:
40
- D:
45
- E:
50
The answer is a.
Alice, while driving to her workplace completes an initial distance of 50 miles in 2 hours and remaining 60 miles in 3 hours. What is the average speed in miles per hour for her entire journey?
22
22.5
40
45
50
|
|
Nikita Singh answered |
Average speed :-
Total distance / Total time
⇒ (50+60) miles / (2+3) hours
⇒ 110/ 5
⇒ 22 miles / hour
Emily rode x miles from her home at a speed of p miles per hour before running out of fuel. She then walked her motorcycle at 8 meters per minute till a few miles further before she met her friend. Emily’s friend dropped her back home, driving along the same route at a rate that was 50% greater than Emily’s riding speed for x miles. If the total journey took t hours, how many miles did Emily walk her motorcycle for? (Given : 1000 meters = 0.62 miles)- a)
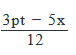
- b)
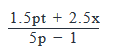
- c)
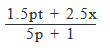
- d)
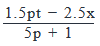
- e)
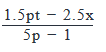
Correct answer is option 'D'. Can you explain this answer?
Emily rode x miles from her home at a speed of p miles per hour before running out of fuel. She then walked her motorcycle at 8 meters per minute till a few miles further before she met her friend. Emily’s friend dropped her back home, driving along the same route at a rate that was 50% greater than Emily’s riding speed for x miles. If the total journey took t hours, how many miles did Emily walk her motorcycle for? (Given : 1000 meters = 0.62 miles)
a)
b)
c)
d)
e)
|
|
Meera Rana answered |
Given:
Let’s call Emily’s journey from her home till she meets her friend as her “Forward Journey” and her journey from when she meets her friend till her home as her “Return Journey”
Forward Journey
- Home to “Ran out of fuel” point
- Distance travelled = x miles
- Driving speed = p miles per hour
- Let the time taken be t1 hours.
- “Ran out of fuel” point till she meets her friend
- Speed of walking= 8 meters per minute
- Let the distance covered be y miles
- Let the time taken while walking = t2 hours.
- Total distance covered in Forward Journey = (x + y) miles
Return Journey
- From when Emily meets her friend to Home
- Total distance travelled = (x + y) miles
- Distance in forward journey = Distance covered in return journey
- Speed of driving = 50% more than p miles per hour
- Let the total time taken for the return journey be t3 hours.
- Total distance travelled = (x + y) miles
So our DST table would look like this:
*(t1 + t2 + t3) = t hours
To Find: How many miles she has walked her motorcycle = y = ?
Linkages
- To find the value of y, let’s focus on the Home to “Ran out of fuel” point row of the DST table.
- To calculate the value of y from here, we need to know the speed and the time, but t2 is unknown to us.
- We observe that t2 is also present in the equation of time (t1 + t2 + t3) = t hours
- To calculate t2 we need the value of t1 and t3.
- We observe that t3 is present in the “Emily meets her friend to home row” of the DST table.
- From here we can express t3 in terms of x, y and p.
- We observe that t1 is present in the Home to “Ran out of fuel” point row of the DST table.
- From here we can express t1 in terms of x and p.
- So we will have 4 equations and 4 variables, and thus we will be able to find the value of y.
Approach
- From the “Emily meets her friend to home” row of the DST table, we will get t3
- in terms of x , y and p.
- From home to “Ran out of fuel” point row of the DST table, we will get t1
- in terms of x and p.
- From “Ran out of fuel point to Emily meets her friend” row of the DST table, we will get t2
- in terms of y.
- Putting values of t1, t2 and t3 in the equation (t1 + t2 + t3) = t hours, we will be able to find the value of unknown i.e. p.
Calculation
- From the “Emily meets her friend to home” row of the DST table, we will get t3 in terms of x , y and p.
2. From home to “Ran out of fuel” point row of the DST table, we will get t1 in terms of x and p.
3. From “Emily “meets her friend” to home row of the DST table, we will get t2 in terms of y.
- Speed = 8 meters per minute
- Here speed is given to us in different units
- Making the units consistent
- Speed =
4. (t1 + t2 + t3) = t hours
- Putting values of t1, t2 and t3, we have
- To get rid of the variable 'p' in the denominator multiply both sides of the equation with 'p'
- So, we get :
To get rid of the decimal in the denominator multiply both sides of the equation by 1/10
- LCM (15,10, 3) = 30
- Multiplying both sides of the equation by 30, we get :
Correct Answer: Option D
Jonathan drove from City A to City B at a rate of 1.2 minutes per kilometer. He then drove back to City A from City B , along the same route, at 1 minute per kilometer. If he took anywhere between 3 hours to 5 hours to travel from City A to City B and between 2 hours to 3 hours on his way back, what could be the distance between the two cities?- a)140 kilometers
- b)160 kilometers
- c)200 kilometers
- d)220 kilometers
- e)270 kilometers
Correct answer is option 'B'. Can you explain this answer?
Jonathan drove from City A to City B at a rate of 1.2 minutes per kilometer. He then drove back to City A from City B , along the same route, at 1 minute per kilometer. If he took anywhere between 3 hours to 5 hours to travel from City A to City B and between 2 hours to 3 hours on his way back, what could be the distance between the two cities?
a)
140 kilometers
b)
160 kilometers
c)
200 kilometers
d)
220 kilometers
e)
270 kilometers

|
Devansh Shah answered |
Jonathan drove from A to B at a rate of 1.2 min per km. He drove between 3 and 5 hours.
t = 3 h = 180 min which is equivalent to 150 km, (You can eliminate A, the minimum value is 150, 140 is out of range)
t = 5 h = 300 min, which is equivalent to 250 km (You can eliminate E, the maximal value is 250, 270 is also out of range)
On the way back Jonathan takes one minute to drive each km.
The trip takes between 2 to 3 hours, so he must have drove between 120 to 180 km. C and D are also out of range, the only possible answer is B
. Jonathan drove 160 km, it is the only value that belongs to both the ranges.
t = 3 h = 180 min which is equivalent to 150 km, (You can eliminate A, the minimum value is 150, 140 is out of range)
t = 5 h = 300 min, which is equivalent to 250 km (You can eliminate E, the maximal value is 250, 270 is also out of range)
On the way back Jonathan takes one minute to drive each km.
The trip takes between 2 to 3 hours, so he must have drove between 120 to 180 km. C and D are also out of range, the only possible answer is B
. Jonathan drove 160 km, it is the only value that belongs to both the ranges.
A speed boat travels at a speed of x miles per hour in still water. With a favourable current, the speed boat travels downstream and reaches its destination in 2.5 hours. The speedboat travels back upstream against the current and covers the same distance in 3.5 hours. If the speed of the current is 1mph, then what is the value of x?- a)2.5
- b)3.5
- c)4
- d)6
- e)9
Correct answer is option 'D'. Can you explain this answer?
A speed boat travels at a speed of x miles per hour in still water. With a favourable current, the speed boat travels downstream and reaches its destination in 2.5 hours. The speedboat travels back upstream against the current and covers the same distance in 3.5 hours. If the speed of the current is 1mph, then what is the value of x?
a)
2.5
b)
3.5
c)
4
d)
6
e)
9

|
Mihir Ghoshal answered |
Given:
- Speed of boat in still water = x mph
- Speed of current = 1 mph
- Time taken downstream = 2.5 hours
- Time taken upstream = 3.5 hours
To find: Speed of boat in still water (x)
Concepts used:
- Speed = Distance/Time
- Let distance be D
- Downstream speed = (x+1) mph
- Upstream speed = (x-1) mph
- Distance downstream = Distance upstream
Solution:
Let distance be D.
Downstream:
- Speed of boat = (x+1) mph
- Time taken = 2.5 hours
- Distance = Speed x Time = (x+1) x 2.5 = 2.5x + 2.5
Upstream:
- Speed of boat = (x-1) mph
- Time taken = 3.5 hours
- Distance = Speed x Time = (x-1) x 3.5 = 3.5x - 3.5
Since distance downstream = distance upstream, we can equate the two expressions:
2.5x + 2.5 = 3.5x - 3.5
Simplifying, we get:
6 = x
Therefore, the speed of the boat in still water is 6 mph.
Answer: Option D.
- Speed of boat in still water = x mph
- Speed of current = 1 mph
- Time taken downstream = 2.5 hours
- Time taken upstream = 3.5 hours
To find: Speed of boat in still water (x)
Concepts used:
- Speed = Distance/Time
- Let distance be D
- Downstream speed = (x+1) mph
- Upstream speed = (x-1) mph
- Distance downstream = Distance upstream
Solution:
Let distance be D.
Downstream:
- Speed of boat = (x+1) mph
- Time taken = 2.5 hours
- Distance = Speed x Time = (x+1) x 2.5 = 2.5x + 2.5
Upstream:
- Speed of boat = (x-1) mph
- Time taken = 3.5 hours
- Distance = Speed x Time = (x-1) x 3.5 = 3.5x - 3.5
Since distance downstream = distance upstream, we can equate the two expressions:
2.5x + 2.5 = 3.5x - 3.5
Simplifying, we get:
6 = x
Therefore, the speed of the boat in still water is 6 mph.
Answer: Option D.
Alan starts his journey from point A at sharp 10.00am. He drives at an average speed of 30 miles per hour and reaches Point B at 11.00 am. Bob starts his journey 15 mins after Alan started his journey and travels via same route as Alan did. If Alan and Bob both reached point B exactly at the same time, then what is Bob’s average speed (in miles per hour)?
- a)35.5
- b)36
- c)37.5
- d)38
- e)40
Correct answer is option 'E'. Can you explain this answer?
Alan starts his journey from point A at sharp 10.00am. He drives at an average speed of 30 miles per hour and reaches Point B at 11.00 am. Bob starts his journey 15 mins after Alan started his journey and travels via same route as Alan did. If Alan and Bob both reached point B exactly at the same time, then what is Bob’s average speed (in miles per hour)?
a)
35.5
b)
36
c)
37.5
d)
38
e)
40

|
Jatin Kapoor answered |
Given:
- Alan starts from point A at 10.00 am and reaches point B at 11.00 am with an average speed of 30 miles per hour.
- Bob starts his journey 15 minutes after Alan (i.e. at 10:15 am) and reaches point B at the same time as Alan.
To find:
The average speed of Bob's journey.
Solution:
Let's first calculate the distance between A and B.
Distance = Speed x Time
Alan traveled from A to B in 1 hour at an average speed of 30 mph.
Distance = 30 x 1 = 30 miles
Now, let's calculate the time taken by Bob to travel from A to B.
Alan started at 10.00 am and reached B at 11.00 am, i.e. he traveled for 1 hour.
Bob started at 10.15 am and reached B at the same time as Alan, i.e. he traveled for 45 minutes.
Therefore, Bob's time taken to travel from A to B = 45 minutes = 0.75 hours
Now we can use the formula of average speed:
Average speed = Total distance / Total time
We know the distance from A to B is 30 miles. Let's calculate the total time taken by Alan and Bob together to reach B:
Total time taken = Bob's time taken + Alan's time taken
Total time taken = 0.75 + 1 = 1.75 hours
Now we can calculate Bob's average speed using the formula:
Average speed = 30 miles / 1.75 hours
Average speed = 17.14 miles per hour
But the answer choices are in integers, so let's round off the answer to the nearest integer:
Average speed = 17 miles per hour ≈ 40 miles per hour
Therefore, the average speed of Bob's journey is 40 miles per hour. Option E is the correct answer.
- Alan starts from point A at 10.00 am and reaches point B at 11.00 am with an average speed of 30 miles per hour.
- Bob starts his journey 15 minutes after Alan (i.e. at 10:15 am) and reaches point B at the same time as Alan.
To find:
The average speed of Bob's journey.
Solution:
Let's first calculate the distance between A and B.
Distance = Speed x Time
Alan traveled from A to B in 1 hour at an average speed of 30 mph.
Distance = 30 x 1 = 30 miles
Now, let's calculate the time taken by Bob to travel from A to B.
Alan started at 10.00 am and reached B at 11.00 am, i.e. he traveled for 1 hour.
Bob started at 10.15 am and reached B at the same time as Alan, i.e. he traveled for 45 minutes.
Therefore, Bob's time taken to travel from A to B = 45 minutes = 0.75 hours
Now we can use the formula of average speed:
Average speed = Total distance / Total time
We know the distance from A to B is 30 miles. Let's calculate the total time taken by Alan and Bob together to reach B:
Total time taken = Bob's time taken + Alan's time taken
Total time taken = 0.75 + 1 = 1.75 hours
Now we can calculate Bob's average speed using the formula:
Average speed = 30 miles / 1.75 hours
Average speed = 17.14 miles per hour
But the answer choices are in integers, so let's round off the answer to the nearest integer:
Average speed = 17 miles per hour ≈ 40 miles per hour
Therefore, the average speed of Bob's journey is 40 miles per hour. Option E is the correct answer.
Every day, Tom walks from his home to his office, via the same route, covering s feet at a speed of x feet per minute. Today he took a different route and ended up walking 10% more than he usually does, at a speed that was 100 meters per minute faster than his usual speed. What is the percentage change in the time he took today compared to the time he takes on a usual day? (1 feet =0.3 meter)
- a)67% decrease
- b)67% increase
- c)10% decrease
- d)10% increase
- e)200% decrease
Correct answer is option 'A'. Can you explain this answer?
Every day, Tom walks from his home to his office, via the same route, covering s feet at a speed of x feet per minute. Today he took a different route and ended up walking 10% more than he usually does, at a speed that was 100 meters per minute faster than his usual speed. What is the percentage change in the time he took today compared to the time he takes on a usual day? (1 feet =0.3 meter)
a)
67% decrease
b)
67% increase
c)
10% decrease
d)
10% increase
e)
200% decrease
|
|
Test Accouint answered |
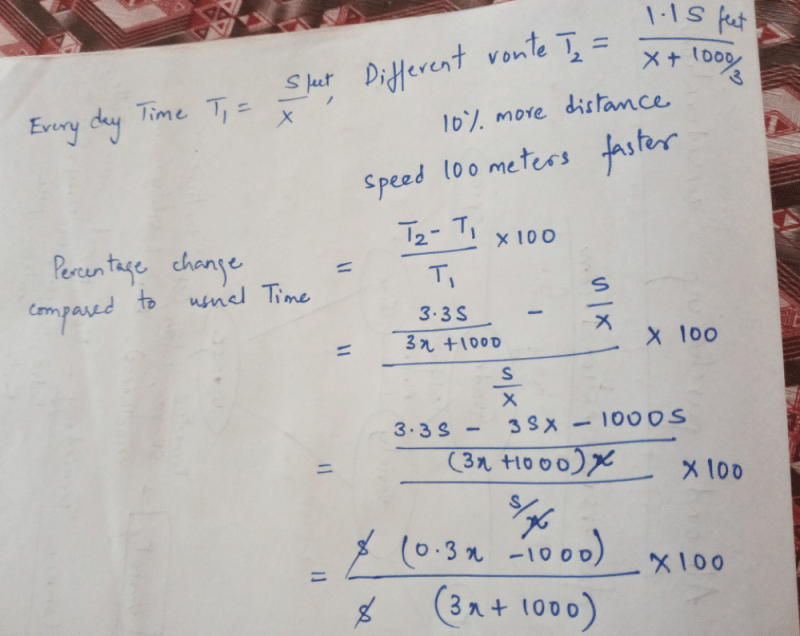
During a trip, Charles covered the first part of a certain distance at an average speed of 30 miles per hour and the remaining part at an average speed of 50 miles per hour. If the ratio of time taken to cover the first part and remaining part is 2: 3, then what is the total distance that Charles travelled?
(1) It took a total of 5 hours to complete the entire distance.
(2) 2/7th of the entire distance was covered during the first part
- a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
- c)BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
During a trip, Charles covered the first part of a certain distance at an average speed of 30 miles per hour and the remaining part at an average speed of 50 miles per hour. If the ratio of time taken to cover the first part and remaining part is 2: 3, then what is the total distance that Charles travelled?
(1) It took a total of 5 hours to complete the entire distance.
(2) 2/7th of the entire distance was covered during the first part
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked, and additional data specific to the problem are needed.

|
Nilotpal Sen answered |
Given information:
- Charles covered the first part of a certain distance at an average speed of 30 miles per hour and the remaining part at an average speed of 50 miles per hour.
- The ratio of time taken to cover the first part and remaining part is 2:3.
To find:
- The total distance that Charles travelled.
Statement 1:
It took a total of 5 hours to complete the entire distance.
This statement alone is not sufficient to answer the question. We know the total time taken but not the distance travelled.
Statement 2:
2/7th of the entire distance was covered during the first part.
This statement alone is not sufficient to answer the question. We know the fraction of the distance covered during the first part but not the actual distance.
Statements 1 and 2:
Using the information from statement 2, we can say that Charles covered 5/7th of the distance at a speed of 50 miles per hour for 3x/5 hours (where x is the total time taken). This means he covered (5/7)*(3x/5) = 3x/7 of the total distance at a speed of 50 miles per hour.
Using the information from statement 1, we know that he covered the remaining 2/7th of the distance in (2/5)x hours at a speed of 30 miles per hour. This means he covered (2/7)*(2/5)x = 4x/35 of the total distance at a speed of 30 miles per hour.
Since the ratio of time taken to cover the first part and remaining part is 2:3, we can say:
(2/5)x/(4x/35) = 2/3
Solving for x, we get x = 7.5 hours.
Using this value of x, we can find the total distance travelled:
Total distance = (2/7)*D + (5/7)*D = D, where D is the distance covered in the entire journey.
Therefore, both statements together are sufficient to answer the question.
Hence, the correct answer is (c) BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
- Charles covered the first part of a certain distance at an average speed of 30 miles per hour and the remaining part at an average speed of 50 miles per hour.
- The ratio of time taken to cover the first part and remaining part is 2:3.
To find:
- The total distance that Charles travelled.
Statement 1:
It took a total of 5 hours to complete the entire distance.
This statement alone is not sufficient to answer the question. We know the total time taken but not the distance travelled.
Statement 2:
2/7th of the entire distance was covered during the first part.
This statement alone is not sufficient to answer the question. We know the fraction of the distance covered during the first part but not the actual distance.
Statements 1 and 2:
Using the information from statement 2, we can say that Charles covered 5/7th of the distance at a speed of 50 miles per hour for 3x/5 hours (where x is the total time taken). This means he covered (5/7)*(3x/5) = 3x/7 of the total distance at a speed of 50 miles per hour.
Using the information from statement 1, we know that he covered the remaining 2/7th of the distance in (2/5)x hours at a speed of 30 miles per hour. This means he covered (2/7)*(2/5)x = 4x/35 of the total distance at a speed of 30 miles per hour.
Since the ratio of time taken to cover the first part and remaining part is 2:3, we can say:
(2/5)x/(4x/35) = 2/3
Solving for x, we get x = 7.5 hours.
Using this value of x, we can find the total distance travelled:
Total distance = (2/7)*D + (5/7)*D = D, where D is the distance covered in the entire journey.
Therefore, both statements together are sufficient to answer the question.
Hence, the correct answer is (c) BOTH statements (1) and (2) TOGETHER are sufficient to answer the question asked, but NEITHER statement ALONE is sufficient to answer the question asked.
A train takes two hours to travel from one station to the other. What is the distance between the two stations? (1) The train covers one third of the total distance in the first hour at an average speed of 80 mph. (2) The average speed during the second hour is 160 mph. - a)Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
- b)Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
- c)BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
- d)EACH statement ALONE is sufficient.
- e)Statements (1) and (2) TOGETHER are NOT sufficient.
Correct answer is option 'A'. Can you explain this answer?
A train takes two hours to travel from one station to the other. What is the distance between the two stations?
(1) The train covers one third of the total distance in the first hour at an average speed of 80 mph.
(2) The average speed during the second hour is 160 mph.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
c)
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
d)
EACH statement ALONE is sufficient.
e)
Statements (1) and (2) TOGETHER are NOT sufficient.

|
Sanskriti Ahuja answered |
Given: The train takes two hours to travel from one station to the other.
To find: The distance between the two stations.
Statement 1: The train covers one third of the total distance in the first hour at an average speed of 80 mph.
Let the total distance be D.
In the first hour, the train covers a distance of D/3 at a speed of 80 mph.
Therefore, time taken to cover D/3 distance = (D/3)/80 = D/240 hours.
Remaining distance = D - D/3 = 2D/3
We do not know the speed at which the train covers this remaining distance.
Hence, statement 1 alone is not sufficient to find the distance between the two stations.
Statement 2: The average speed during the second hour is 160 mph.
Let the distance covered in the second hour be x.
Therefore, time taken to cover x distance = x/160 hours.
Distance covered in the first hour = 2x/3.
Therefore, time taken to cover 2x/3 distance = (2x/3)/80 = x/120 hours.
Total time taken to cover the distance = (x/160) + (x/120) = 2 hours.
Simplifying, we get x = 240.
Hence, statement 2 alone is sufficient to find the distance between the two stations.
Therefore, the correct answer is option A, i.e., statement 1 alone is not sufficient, but statement 2 alone is sufficient.
To find: The distance between the two stations.
Statement 1: The train covers one third of the total distance in the first hour at an average speed of 80 mph.
Let the total distance be D.
In the first hour, the train covers a distance of D/3 at a speed of 80 mph.
Therefore, time taken to cover D/3 distance = (D/3)/80 = D/240 hours.
Remaining distance = D - D/3 = 2D/3
We do not know the speed at which the train covers this remaining distance.
Hence, statement 1 alone is not sufficient to find the distance between the two stations.
Statement 2: The average speed during the second hour is 160 mph.
Let the distance covered in the second hour be x.
Therefore, time taken to cover x distance = x/160 hours.
Distance covered in the first hour = 2x/3.
Therefore, time taken to cover 2x/3 distance = (2x/3)/80 = x/120 hours.
Total time taken to cover the distance = (x/160) + (x/120) = 2 hours.
Simplifying, we get x = 240.
Hence, statement 2 alone is sufficient to find the distance between the two stations.
Therefore, the correct answer is option A, i.e., statement 1 alone is not sufficient, but statement 2 alone is sufficient.
Phil drives east from his home for 2 hours before realizing that he will run out of fuel in another 70 miles. Nevertheless, he drives for another 10 miles east before returning back home via the same route. If he drives at a constant speed throughout his journey and returns home with fuel left for another 10 miles, how much time does he take for his journey eastwards?- a)2.0 hours
- b)2.5 hours
- c)3.0 hours
- d)3.5 hours
- e)Cannot be determined
Correct answer is option 'B'. Can you explain this answer?
Phil drives east from his home for 2 hours before realizing that he will run out of fuel in another 70 miles. Nevertheless, he drives for another 10 miles east before returning back home via the same route. If he drives at a constant speed throughout his journey and returns home with fuel left for another 10 miles, how much time does he take for his journey eastwards?
a)
2.0 hours
b)
2.5 hours
c)
3.0 hours
d)
3.5 hours
e)
Cannot be determined

|
Sankar Desai answered |
Given:
- Phil drives east from his home for 2 hours before realizing that he will run out of fuel in another 70 miles.
- He drives for another 10 miles east before returning back home via the same route.
- He returns home with fuel left for another 10 miles.
- He drives at a constant speed throughout his journey.
To find: How much time does Phil take for his journey eastwards?
Approach:
Let's first find out how far Phil drove eastwards before returning home.
Distance traveled eastward = (2 hours of driving before realizing he will run out of fuel) * (his constant speed)
= 2s (where s is his constant speed)
After realizing that he will run out of fuel, he drives for another 10 miles eastward before turning back. So the total distance traveled eastward before returning home = 70 + 10 = 80 miles.
Now, let's find out how far Phil could have traveled with the fuel left for another 10 miles.
Distance traveled westward with the remaining fuel = 10 miles
So the total distance traveled by Phil = Distance traveled eastward + Distance traveled westward with the remaining fuel
= 80 + 10 = 90 miles
We know that Phil drove at a constant speed throughout his journey. Let's assume his speed to be 's' miles per hour. Then we can use the formula for distance, speed, and time: distance = speed * time.
So, time taken for the journey eastwards = (distance traveled eastwards) / (speed)
= (2s + 80) / s
= 2 + 80/s
Now, we are given that Phil returns home with fuel left for another 10 miles. This means that he had to travel the same distance (90 miles) on his return journey as well. So, we can use the same formula to find the time taken for his return journey:
Time taken for the return journey = (distance traveled westward with the remaining fuel) / (speed)
= 10 / s
The total time taken for the entire journey = time taken for the journey eastwards + time taken for the return journey
= 2 + 80/s + 10/s
= 2 + 90/s
We need to find the value of 's' to get the total time taken. Unfortunately, we don't have enough information to do that. So, the answer is 'Cannot be determined'.
Therefore, the correct answer is option 'E'.
- Phil drives east from his home for 2 hours before realizing that he will run out of fuel in another 70 miles.
- He drives for another 10 miles east before returning back home via the same route.
- He returns home with fuel left for another 10 miles.
- He drives at a constant speed throughout his journey.
To find: How much time does Phil take for his journey eastwards?
Approach:
Let's first find out how far Phil drove eastwards before returning home.
Distance traveled eastward = (2 hours of driving before realizing he will run out of fuel) * (his constant speed)
= 2s (where s is his constant speed)
After realizing that he will run out of fuel, he drives for another 10 miles eastward before turning back. So the total distance traveled eastward before returning home = 70 + 10 = 80 miles.
Now, let's find out how far Phil could have traveled with the fuel left for another 10 miles.
Distance traveled westward with the remaining fuel = 10 miles
So the total distance traveled by Phil = Distance traveled eastward + Distance traveled westward with the remaining fuel
= 80 + 10 = 90 miles
We know that Phil drove at a constant speed throughout his journey. Let's assume his speed to be 's' miles per hour. Then we can use the formula for distance, speed, and time: distance = speed * time.
So, time taken for the journey eastwards = (distance traveled eastwards) / (speed)
= (2s + 80) / s
= 2 + 80/s
Now, we are given that Phil returns home with fuel left for another 10 miles. This means that he had to travel the same distance (90 miles) on his return journey as well. So, we can use the same formula to find the time taken for his return journey:
Time taken for the return journey = (distance traveled westward with the remaining fuel) / (speed)
= 10 / s
The total time taken for the entire journey = time taken for the journey eastwards + time taken for the return journey
= 2 + 80/s + 10/s
= 2 + 90/s
We need to find the value of 's' to get the total time taken. Unfortunately, we don't have enough information to do that. So, the answer is 'Cannot be determined'.
Therefore, the correct answer is option 'E'.
To reach her office from her home, Karen traveled x miles at a speed of y miles per hour. On her way back, via the same route, she travels for ten miles before stopping for an hour. If Karen drove at y miles per hour till she stopped, by what percentage should she increase her speed so that the overall time taken to reach back home from the office is the same as that taken to reach the office from home?
- a)
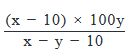
- b)
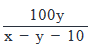
- c)
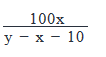
- d)
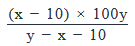
- e)
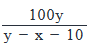
Correct answer is option 'B'. Can you explain this answer?
To reach her office from her home, Karen traveled x miles at a speed of y miles per hour. On her way back, via the same route, she travels for ten miles before stopping for an hour. If Karen drove at y miles per hour till she stopped, by what percentage should she increase her speed so that the overall time taken to reach back home from the office is the same as that taken to reach the office from home?
a)
b)
c)
d)
e)

|
Preitee Ranjan Pradhan answered |

Robert and Timothy both left their respective homes at 1 PM. Robert walked till a lake that was between 2.5 kilometres and 3 kilometres from his home, inclusive, and returned home between 1:55 PM and 2:05 PM. If Timothy walked 5 kilometres more than Robert and returned to her home at 3 PM, which of the following statements must be true?I. The walking speed of Timothy was greater than that of RobertII. Robert’s walking speed was close to 3 kilometers per hourIII. Had Robert covered 5 more meters every 18 seconds, his walking speed would have been greater than Timothy’s- a)I only
- b)II only
- c)III only
- d)I, II and III
- e)None of the above
Correct answer is option 'C'. Can you explain this answer?
Robert and Timothy both left their respective homes at 1 PM. Robert walked till a lake that was between 2.5 kilometres and 3 kilometres from his home, inclusive, and returned home between 1:55 PM and 2:05 PM. If Timothy walked 5 kilometres more than Robert and returned to her home at 3 PM, which of the following statements must be true?
I. The walking speed of Timothy was greater than that of Robert
II. Robert’s walking speed was close to 3 kilometers per hour
III. Had Robert covered 5 more meters every 18 seconds, his walking speed would have been greater than Timothy’s
a)
I only
b)
II only
c)
III only
d)
I, II and III
e)
None of the above

|
Sharmila Nambiar answered |
Given:
- Robert
- Let the distance covered be DR and time taken be TR
- 2.5*2 km ≤ DR ≤ 3*2 (distance in round trip is double the one-way distance)
- Timothy
- Let the distance covered be DT and time taken be TT
- As Timothy walked 5 kilometers more than Robert, she would have walked a minimum distance of 5 + 5 = 10 kms and a maximum distance of 6 + 5 = 11 kms.
- So, 10 km ≤ DT ≤ 11
- TT = 2 hours
To Find:
Let Robert’s speed be SR and Timothy’s speed be ST
ST > SR?
SR ∼ 3 kmph?
SR ∼ 3 kmph?
Approach:
- Find range of SR and ST (since definite values of DR, TR and TT are not given, definite values of SR and ST cannot be found)
- Check the validity of the 3 statements
Working out:
- Range of ST
- SR + 1 kmph: 5.6 kmph – 7.7 kmph
- Thus, Robert’s speed would definitely have been greater than
- Timothy’s
- So, Yes
Thus, only St. III is a must be true statement.
Correct Answer = Option C
Correct Answer = Option C
Bob bikes to school every day at a steady rate of x miles per hour. On a particular day, Bob had a flat tire exactly halfway to school. He immediately started walking to school at a steady pace of y miles per hour. He arrived at school exactly t hours after leaving his home. How many miles is it from the school to Bob's home?- a)(x + y) / t
- b)2(x + t) / xy
- c)2xyt / (x + y)
- d)2(x + y + t) / xy
- e)x(y + t) + y(x + t)
Correct answer is option 'C'. Can you explain this answer?
Bob bikes to school every day at a steady rate of x miles per hour. On a particular day, Bob had a flat tire exactly halfway to school. He immediately started walking to school at a steady pace of y miles per hour. He arrived at school exactly t hours after leaving his home. How many miles is it from the school to Bob's home?
a)
(x + y) / t
b)
2(x + t) / xy
c)
2xyt / (x + y)
d)
2(x + y + t) / xy
e)
x(y + t) + y(x + t)

|
Pallabi Sengupta answered |
Let b be the number of hours Bob spends biking. Then (t – b) is the number of hours he spends walking. Let d be the distance in miles from his home to school. Since he had the flat tire halfway to school, he biked d/2 miles and he walked d/2 miles. Now we can set up the equations using the formula rate x time = distance. Remember that we want to solve for d, the total distance from Bob's home to school.
1) xb = d/2
2) y(t – b) = d/2
2) y(t – b) = d/2
Solving equation 1) for b gives us:
3) b = d/2x Substituting this value of b into equation 2 gives:
4) y(t – d/2x) = d/2 Multiply both sides by 2x:
5) 2xy(t – d/2x) = dx Distribute the 2xy
6) 2xyt – dy = dx Add dy to both sides to collect the d's on one side.
7) 2xyt = dx + dy Factor out the d
8) 2xyt = d(x + y) Divide both sides by (x + y) to solve for d
9) 2xyt / (x + y) = d
The correct answer is C.
Lexy walks 5 miles from point A to point B in one hour, then bicycles back to point A along the same route at 15 miles per hour. Ben makes the same round trip, but does so at half of Lexy’s average speed. How many minutes does Ben spend on his round trip?- a)40
- b)80
- c)120
- d)160
- e)180
Correct answer is option 'D'. Can you explain this answer?
Lexy walks 5 miles from point A to point B in one hour, then bicycles back to point A along the same route at 15 miles per hour. Ben makes the same round trip, but does so at half of Lexy’s average speed. How many minutes does Ben spend on his round trip?
a)
40
b)
80
c)
120
d)
160
e)
180

|
Navya Yadav answered |
We begin by figuring out Lexy’s average speed. On her way from A to B, she travels 5 miles in one hour, so her speed is 5 miles per hour. On her way back from B to A, she travels the same 5 miles at 15 miles per hour. Her average speed for the round trip is NOT simply the average of these two speeds. Rather, her average speed must be computed using the formula RT = D, where R is rate, T is time and D is distance. Her average speed for the whole trip is the total distance of her trip divided by the total time of her trip.
We already know that she spends 1 hour going from A to B. When she returns from B to A, Lexy travels 5 miles at a rate of 15 miles per hour, so our formula tells us that 15T = 5, or T = 1/3. In other words, it only takes Lexy 1/3 of an hour, or 20 minutes, to return from B to A. Her total distance traveled for the round trip is 5+5=10 miles and her total time is 1+1/3=4/3 of an hour, or 80 minutes.
We have to give our final answer in minutes, so it makes sense to find Lexy's average rate in miles per minute, rather than miles per hour. 10 miles / 80 minutes = 1/8 miles per minute. This is Lexy's average rate.
We are told that Ben's rate is half of Lexy's, so he must be traveling at 1/16 miles per minute. He also travels a total of 10 miles, so (1/16)T = 10, or T = 160. Ben's round trip takes 160 minutes.
We are told that Ben's rate is half of Lexy's, so he must be traveling at 1/16 miles per minute. He also travels a total of 10 miles, so (1/16)T = 10, or T = 160. Ben's round trip takes 160 minutes.
Alternatively, we could use a shortcut for the last part of this problem. We know that Ben's rate is half of Lexy's average rate. This means that, for the entire trip, Ben will take twice as long as Lexy to travel the same distance. Once we determine that Lexy will take 80 minutes to complete the round trip, we can double the figure to get Ben's time. 80 × 2 = 160.
The correct answer is D.
Tom and Linda stand at point A. Linda begins to walk in a straight line away from Tom at a constant rate of 2 miles per hour. One hour later, Tom begins to jog in a straight line in the exact opposite direction at a constant rate of 6 miles per hour. If both Tom and Linda travel indefinitely, what is the positive difference, in minutes, between the amount of time it takes Tom to cover half of the distance that Linda has covered and the amount of time it takes Tom to cover twice the distance that Linda has covered?- a)60
- b)72
- c)84
- d)90
- e)108
Correct answer is option 'E'. Can you explain this answer?
Tom and Linda stand at point A. Linda begins to walk in a straight line away from Tom at a constant rate of 2 miles per hour. One hour later, Tom begins to jog in a straight line in the exact opposite direction at a constant rate of 6 miles per hour. If both Tom and Linda travel indefinitely, what is the positive difference, in minutes, between the amount of time it takes Tom to cover half of the distance that Linda has covered and the amount of time it takes Tom to cover twice the distance that Linda has covered?
a)
60
b)
72
c)
84
d)
90
e)
108

|
Pallabi Sengupta answered |
The formula to calculate distance is Distance = (Rate)(Time). So at any given moment Tom's distance (let's call it DT) can be expressed as DT = 6T. So, at any given moment, Linda's distance (let's call it DL) can be expressed as DL = 2(T + 1) (remember, Linda's time is one hour more than Tom's). The question asks us to find the positive difference between the amount of time it takes Tom to cover half of Linda's distance and the time it takes him to cover twice her distance. Let's find each time separately first.
When Tom has covered half of Linda's distance, the following equation will hold: 6T = (2(T + 1))/2. We can solve for T:
6T = (2(T + 1))/2
6T = (2T + 2)/2
6T = T +1
5T = 1
T = 1/5
6T = (2(T + 1))/2
6T = (2T + 2)/2
6T = T +1
5T = 1
T = 1/5
So it will take Tom 1/5 hours, or 12 minutes, to cover half of Linda's distance. When Tom has covered twice Linda's distance, the following equation will hold: 6T = 2(2(T + 1). We can solve for T:
6T = 2(2(T + 1)
6T = 2(2T + 2)
6T = 4T + 4
2T = 4
T = 2
6T = 2(2T + 2)
6T = 4T + 4
2T = 4
T = 2
So it will take Tom 2 hours, or 120 minutes, to cover twice Linda's distance.
We need to find the positive difference between these times: 120 – 12 = 108.
We need to find the positive difference between these times: 120 – 12 = 108.
The correct answer is E.
Two dogs are running towards each other from opposite ends of a two-mile track. Dog 1 has a speed of 12 mph and Dog 2 has a speed of 8 mph. How many miles from Dog 1’s starting position will they meet?- a)1
- b)6/5
- c)5/4
- d)4/3
- e)3/2
Correct answer is option 'B'. Can you explain this answer?
Two dogs are running towards each other from opposite ends of a two-mile track. Dog 1 has a speed of 12 mph and Dog 2 has a speed of 8 mph. How many miles from Dog 1’s starting position will they meet?
a)
1
b)
6/5
c)
5/4
d)
4/3
e)
3/2

|
Nilotpal Sen answered |
To solve this problem, we can use the concept of relative speed. Relative speed is the difference between the speeds of two objects moving in opposite directions.
Let's assume that the dogs meet after t hours. In that time, Dog 1 would have traveled a distance of 12t miles, and Dog 2 would have traveled a distance of 8t miles.
The total distance between the dogs is 2 miles, so we can set up the equation:
12t + 8t = 2
20t = 2
t = 2/20
t = 1/10 hour
Therefore, the dogs will meet after 1/10 hour.
To find the distance from Dog 1's starting position, we can substitute the value of t into the distance formula:
Distance = Speed × Time
Distance = 12 × 1/10
Distance = 12/10
Distance = 6/5 miles
Hence, the dogs will meet 6/5 miles from Dog 1's starting position.
Therefore, the correct answer is option B) 6/5.
Let's assume that the dogs meet after t hours. In that time, Dog 1 would have traveled a distance of 12t miles, and Dog 2 would have traveled a distance of 8t miles.
The total distance between the dogs is 2 miles, so we can set up the equation:
12t + 8t = 2
20t = 2
t = 2/20
t = 1/10 hour
Therefore, the dogs will meet after 1/10 hour.
To find the distance from Dog 1's starting position, we can substitute the value of t into the distance formula:
Distance = Speed × Time
Distance = 12 × 1/10
Distance = 12/10
Distance = 6/5 miles
Hence, the dogs will meet 6/5 miles from Dog 1's starting position.
Therefore, the correct answer is option B) 6/5.
Alice travels at an average speed of 60miles per hour from her home to a grocery store. She travels back to her home via same route at an average speed of 80 miles per hour. What is the average speed of her entire journey?
- a)
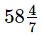
- b)
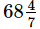
- c)70
- d)75
- e)82
Correct answer is option 'B'. Can you explain this answer?
Alice travels at an average speed of 60miles per hour from her home to a grocery store. She travels back to her home via same route at an average speed of 80 miles per hour. What is the average speed of her entire journey?
a)
b)
c)
70
d)
75
e)
82

|
EduRev GMAT answered |
2xaxb
a+b
2x60x80
60+80
2x6x80
14
480
7
so (b) option
a+b
2x60x80
60+80
2x6x80
14
480
7
so (b) option
Two trains start from City A and travel towards City B, which is at a distance of 100 miles from City A, at the same time with an
average speeds of 60 miles per hour and 80 miles per hour respectively. A train starts from City B at the same time and travels towards City A at an average speed of 70 miles per hour. How far from city B is the slower train starting from City A when the faster train starting from City A meets the train starting from City B?- a)30 miles
- b)40 miles
- c)50 miles
- d)60 miles
- e)70 miles
Correct answer is option 'D'. Can you explain this answer?
Two trains start from City A and travel towards City B, which is at a distance of 100 miles from City A, at the same time with an
average speeds of 60 miles per hour and 80 miles per hour respectively. A train starts from City B at the same time and travels towards City A at an average speed of 70 miles per hour. How far from city B is the slower train starting from City A when the faster train starting from City A meets the train starting from City B?
average speeds of 60 miles per hour and 80 miles per hour respectively. A train starts from City B at the same time and travels towards City A at an average speed of 70 miles per hour. How far from city B is the slower train starting from City A when the faster train starting from City A meets the train starting from City B?
a)
30 miles
b)
40 miles
c)
50 miles
d)
60 miles
e)
70 miles

|
Saumya Shah answered |
Problem:
Two trains start from City A and travel towards City B, which is at a distance of 100 miles from City A, at the same time with an average speeds of 60 miles per hour and 80 miles per hour respectively. A train starts from City B at the same time and travels towards City A at an average speed of 70 miles per hour. How far from city B is the slower train starting from City A when the faster train starting from City A meets the train starting from City B?
Solution:
Let the distance of the slower train from City B be x miles.
The time taken by both the trains starting from City A to meet is given by:
t = d / (v1 + v2)
Where d is the distance between the cities, v1 is the speed of the slower train, and v2 is the speed of the faster train.
So, the time taken by both the trains starting from City A to meet is:
t = 100 / (60 + 80) = 5/6 hours
In this time, the faster train starting from City A covers a distance of:
d1 = v2 * t = 80 * 5/6 = 400/6 miles
The slower train starting from City A covers a distance of:
d2 = v1 * t = 60 * 5/6 = 50 miles
Now, the train starting from City B is also traveling towards the slower train starting from City A. So, we need to find the time taken by the train starting from City B to meet the slower train starting from City A.
The time taken by the train starting from City B to meet the slower train starting from City A is given by:
t' = x / (v1 + v3)
Where v3 is the speed of the train starting from City B.
In the same time t', the train starting from City B covers a distance of:
d3 = v3 * t' = 70 * t'
Now, the distance covered by the slower train starting from City A in the same time t' is:
d4 = v1 * t' = 60 * t'
So, when the faster train starting from City A meets the train starting from City B, the slower train starting from City A has covered a distance of:
x + d4 = x + 60 * t'
But we know that the time taken by both the trains starting from City A to meet is 5/6 hours, which is the same as the time taken by the train starting from City B to meet the slower train starting from City A. So, we can equate the distances covered by the train starting from City B and the slower train starting from City A:
d3 = x + 60 * t'
Substituting the value of t' from the above equation, we get:
70 * t' = x + 60 * t'
Or, x = 10 * t'
Substituting the value of t' from the above equation, we get:
x = 10 * (d3 / 70)
Substituting the value of d3, we get:
x = 10 * (400 / 7)
Simplifying, we get:
x = 57.14 miles
Therefore, the slower train starting from City A is 57.14 miles from City B when the faster train starting from City A
Two trains start from City A and travel towards City B, which is at a distance of 100 miles from City A, at the same time with an average speeds of 60 miles per hour and 80 miles per hour respectively. A train starts from City B at the same time and travels towards City A at an average speed of 70 miles per hour. How far from city B is the slower train starting from City A when the faster train starting from City A meets the train starting from City B?
Solution:
Let the distance of the slower train from City B be x miles.
The time taken by both the trains starting from City A to meet is given by:
t = d / (v1 + v2)
Where d is the distance between the cities, v1 is the speed of the slower train, and v2 is the speed of the faster train.
So, the time taken by both the trains starting from City A to meet is:
t = 100 / (60 + 80) = 5/6 hours
In this time, the faster train starting from City A covers a distance of:
d1 = v2 * t = 80 * 5/6 = 400/6 miles
The slower train starting from City A covers a distance of:
d2 = v1 * t = 60 * 5/6 = 50 miles
Now, the train starting from City B is also traveling towards the slower train starting from City A. So, we need to find the time taken by the train starting from City B to meet the slower train starting from City A.
The time taken by the train starting from City B to meet the slower train starting from City A is given by:
t' = x / (v1 + v3)
Where v3 is the speed of the train starting from City B.
In the same time t', the train starting from City B covers a distance of:
d3 = v3 * t' = 70 * t'
Now, the distance covered by the slower train starting from City A in the same time t' is:
d4 = v1 * t' = 60 * t'
So, when the faster train starting from City A meets the train starting from City B, the slower train starting from City A has covered a distance of:
x + d4 = x + 60 * t'
But we know that the time taken by both the trains starting from City A to meet is 5/6 hours, which is the same as the time taken by the train starting from City B to meet the slower train starting from City A. So, we can equate the distances covered by the train starting from City B and the slower train starting from City A:
d3 = x + 60 * t'
Substituting the value of t' from the above equation, we get:
70 * t' = x + 60 * t'
Or, x = 10 * t'
Substituting the value of t' from the above equation, we get:
x = 10 * (d3 / 70)
Substituting the value of d3, we get:
x = 10 * (400 / 7)
Simplifying, we get:
x = 57.14 miles
Therefore, the slower train starting from City A is 57.14 miles from City B when the faster train starting from City A
James started from his home and drove eastwards at a constant speed. Exactly 90 minutes after James stated from his home, his brother Patrick started from the same point and drove in the same direction as James did at a different constant speed. Patrick overtook James exactly 90 minutes after Patrick started his journey and then continued driving at the same speed for another 2 hours. By what percentage should Patrick reduce his speed so that James could catch up with Patrick in exactly 8 hours after Patrick overtook James?- a)25%
- b)33%
- c)50%
- d)67%
- e)75%
Correct answer is option 'D'. Can you explain this answer?
James started from his home and drove eastwards at a constant speed. Exactly 90 minutes after James stated from his home, his brother Patrick started from the same point and drove in the same direction as James did at a different constant speed. Patrick overtook James exactly 90 minutes after Patrick started his journey and then continued driving at the same speed for another 2 hours. By what percentage should Patrick reduce his speed so that James could catch up with Patrick in exactly 8 hours after Patrick overtook James?
a)
25%
b)
33%
c)
50%
d)
67%
e)
75%

|
Sonal Banerjee answered |
Given information:
- James drove eastwards at a constant speed.
- Patrick started from the same point 90 minutes later and drove in the same direction as James did at a different constant speed.
- Patrick overtook James after 90 minutes and continued driving at the same speed for another 2 hours.
- We need to find the percentage by which Patrick should reduce his speed so that James could catch up with Patrick in exactly 8 hours after Patrick overtook James.
Calculating the distance covered by James and Patrick:
Let's assume that James' speed is x and Patrick's speed is y.
Distance covered by James in 90 minutes = x * 1.5 = 1.5x
When Patrick overtakes James, the distance covered by Patrick = distance covered by James + 90 minutes of driving time.
So, distance covered by Patrick = x * 1.5 + y * 1.5 = 1.5(x + y)
Distance covered by Patrick in the next 2 hours = 2y
Calculating the time taken by James to catch up with Patrick:
Let's assume that James catches up with Patrick after t hours.
Distance covered by James in t hours = x * t
Distance covered by Patrick in t hours = 1.5(x + y) + 2y = 1.5x + 3.5y
As both of them cover the same distance when James catches up with Patrick, we can equate the above two equations:
x * t = 1.5x + 3.5y
t = 1.5 + 3.5y/x
Calculating the percentage reduction in Patrick's speed:
As per the question, we need to find the percentage by which Patrick should reduce his speed so that James could catch up with Patrick in exactly 8 hours after Patrick overtook James.
So, t = 8 - 1.5 - 2 = 4.5
From the above equation, we can say that t is inversely proportional to x/y.
So, if Patrick reduces his speed by a factor of k, then y = (1/k) * y
Now, t = 1.5 + 3.5y/x becomes t = 1.5 + 3.5[k * (y/x)]
Simplifying, we get t = 1.5 + 3.5/k
So, 4.5 = 1.5 + 3.5/k
k = 3.5/3
k = 1.167
Percentage reduction in Patrick's speed = (1 - 1.167) * 100 = 67%
Therefore, the correct answer is option D - 67%.
- James drove eastwards at a constant speed.
- Patrick started from the same point 90 minutes later and drove in the same direction as James did at a different constant speed.
- Patrick overtook James after 90 minutes and continued driving at the same speed for another 2 hours.
- We need to find the percentage by which Patrick should reduce his speed so that James could catch up with Patrick in exactly 8 hours after Patrick overtook James.
Calculating the distance covered by James and Patrick:
Let's assume that James' speed is x and Patrick's speed is y.
Distance covered by James in 90 minutes = x * 1.5 = 1.5x
When Patrick overtakes James, the distance covered by Patrick = distance covered by James + 90 minutes of driving time.
So, distance covered by Patrick = x * 1.5 + y * 1.5 = 1.5(x + y)
Distance covered by Patrick in the next 2 hours = 2y
Calculating the time taken by James to catch up with Patrick:
Let's assume that James catches up with Patrick after t hours.
Distance covered by James in t hours = x * t
Distance covered by Patrick in t hours = 1.5(x + y) + 2y = 1.5x + 3.5y
As both of them cover the same distance when James catches up with Patrick, we can equate the above two equations:
x * t = 1.5x + 3.5y
t = 1.5 + 3.5y/x
Calculating the percentage reduction in Patrick's speed:
As per the question, we need to find the percentage by which Patrick should reduce his speed so that James could catch up with Patrick in exactly 8 hours after Patrick overtook James.
So, t = 8 - 1.5 - 2 = 4.5
From the above equation, we can say that t is inversely proportional to x/y.
So, if Patrick reduces his speed by a factor of k, then y = (1/k) * y
Now, t = 1.5 + 3.5y/x becomes t = 1.5 + 3.5[k * (y/x)]
Simplifying, we get t = 1.5 + 3.5/k
So, 4.5 = 1.5 + 3.5/k
k = 3.5/3
k = 1.167
Percentage reduction in Patrick's speed = (1 - 1.167) * 100 = 67%
Therefore, the correct answer is option D - 67%.
Two siblings Mark and Steve start from the same point and walk in the same direction at speeds of 5 kilometres per hour and 10 kilometres per hour respectively. After walking for an hour, Mark turns around and walks back along the same path to the starting point. Mark rests for half an hour at the starting point, and then hires a taxi driving at 30 kilometres per hour to catch up with Steve. If the taxi charges $10 for the first 2 kilometres and $2 for every subsequent 500 metres, how much in dollars does Mark pay for the taxi ride?- a)92
- b)102
- c)142
- d)152
- e)160
Correct answer is option 'D'. Can you explain this answer?
Two siblings Mark and Steve start from the same point and walk in the same direction at speeds of 5 kilometres per hour and 10 kilometres per hour respectively. After walking for an hour, Mark turns around and walks back along the same path to the starting point. Mark rests for half an hour at the starting point, and then hires a taxi driving at 30 kilometres per hour to catch up with Steve. If the taxi charges $10 for the first 2 kilometres and $2 for every subsequent 500 metres, how much in dollars does Mark pay for the taxi ride?
a)
92
b)
102
c)
142
d)
152
e)
160

|
Abhishek Choudhury answered |
Given:
- Speed of Mark = 5 kilometres per hour
- Speed of Steve = 10 kilometres per hour
- Time after which Mark turns around and walks back = 1 hour
- Time for which Mark rests = 0.5 hour
- Speed of taxi = 30 kilometres per hour
- Charges for the first 2 kilometres = $10
- Chrages for every subsequent 500 metres = $2
To Find: Amount that Mark paid to the taxi driver?
Approach:
- For finding the amount that Mark paid to the taxi driver, we need to find the distance travelled by the taxi.
- As the taxi started from the starting point of Steve and stopped when it caught up with Steve, the (Distance travelled by the taxi) = (Distance travelled by Steve since he started walking)
- Distance travelled by Steve = Speed of Steve * Time taken
- We are given that speed of steve = 10 kilometres per hour. We need to find the time for which Steve travelled
- The travelling time of Steve can be divided into 4 phases:
- Phase-I: Time for which Mark and Steve both walked = 1 hour
- Phase-II: Time taken by Mark to reach back the starting point = 1hour
- As Mark travelled one way for 1 hour and travelled back the same path at the same speed, he will take the same time
- Please note that Steve kept walking ahead during this time
- Phase-III: Time for which Mark rests = 0.5 hour
- Plesae note that Steve kept walking ahead during this time
- Phase-IV: Time for which the taxi drove = t hours
- For this phase, the distance travelled by taxi = total distance travelled by Steve
- The time for which the taxi would travel would be equal to the time for which Steve would be travelling in this phase.
- As we know the speeds of both taxi and Steve, we can formulate an equation by equating the time taken.
- We will find the distance travelled by Steve in each of the phases and then sum it up to get the total distance distance travelled by Steve
Working out:
- Phase-I: Distance travelled by Steve = 10 * 1 = 10 kilometres
- Phase-II: Distance travelled by Steve = 10 * 1 = 10 kilomtres
- Phase-III: Disatnce travelled by Steve = 10 * 0.5 = 5 kilomtres
- Phase-IV:
- Let the distance covered by Steve in time t hours be x kilometres.
- Total distance covered by taxi to catch up with Steve = 10 + 10 + 5 + x = 25 + x kilometres
- Time taken by taxi to cover 25 + x kilometres, i.e. t =
- Time taken by taxi to cover 25 + x kilometres, i.e. t =
- We can equate the time taken by taxi and Steve
-
-
- Let the distance covered by Steve in time t hours be x kilometres.
- So, total distance travelled by the taxi = 25 + 12.5 = 37.5 kilomtres
- Charges for the first 2 kilometres = $10
- Charges for the rest 35.5 kilomtres = 35.5 * 2 * 2 = $142
- Hence, total amount paid to the taxi driver = $10 + $ 142 = $152.
Answer : D
On Monday, Lou drives his ford escort with 28-inch tires, averaging x miles per hour. On Tuesday, Lou
switches the tires on his car to 32-inch tires yet drives to work at the same average speed as on Monday. What is the percent change from Monday to Tuesday in the average number of revolutions that Lou’s tires make per second?- a)Decrease by 14.3%
- b)Decrease by 12.5%
- c)Increase by 14.3%
- d)Increase by 12.5%
- e)cannot be determined with the given information
Correct answer is option 'B'. Can you explain this answer?
On Monday, Lou drives his ford escort with 28-inch tires, averaging x miles per hour. On Tuesday, Lou
switches the tires on his car to 32-inch tires yet drives to work at the same average speed as on Monday. What is the percent change from Monday to Tuesday in the average number of revolutions that Lou’s tires make per second?
switches the tires on his car to 32-inch tires yet drives to work at the same average speed as on Monday. What is the percent change from Monday to Tuesday in the average number of revolutions that Lou’s tires make per second?
a)
Decrease by 14.3%
b)
Decrease by 12.5%
c)
Increase by 14.3%
d)
Increase by 12.5%
e)
cannot be determined with the given information

|
Niharika Sen answered |
To solve this problem, we need to consider the relationship between the distance traveled and the number of revolutions.
The distance traveled is directly proportional to the number of revolutions. This means that if the distance traveled remains the same, the number of revolutions will also remain the same.
Since Lou drives to work at the same average speed on both Monday and Tuesday, the distance traveled will remain the same. Therefore, the number of revolutions will also remain the same.
This means that there is no percent change from Monday to Tuesday in the average number of revolutions. It remains constant at 100%.
The distance traveled is directly proportional to the number of revolutions. This means that if the distance traveled remains the same, the number of revolutions will also remain the same.
Since Lou drives to work at the same average speed on both Monday and Tuesday, the distance traveled will remain the same. Therefore, the number of revolutions will also remain the same.
This means that there is no percent change from Monday to Tuesday in the average number of revolutions. It remains constant at 100%.
Alex and Hales started rowing towards one another at constant speeds and met after rowing for an hour. The initial distance between Alex and Hales was 20 kilometers and Alex rowed downstream while Hales rowed upstream during this journey. On some other day, the time taken by Alex alone, rowing at the same constant speed, to cover the distance between these two points going upstream was 75 minutes more than the time taken by him to cover the same distance going downstream. What was the time taken in hours by Hales to cover 20 kilometers going upstream? Assume the speed of the stream to be 4 kilometers per hour- a)1.25
- b)1.6
- c)2.5
- d)5
- e)8
Correct answer is option 'D'. Can you explain this answer?
Alex and Hales started rowing towards one another at constant speeds and met after rowing for an hour. The initial distance between Alex and Hales was 20 kilometers and Alex rowed downstream while Hales rowed upstream during this journey. On some other day, the time taken by Alex alone, rowing at the same constant speed, to cover the distance between these two points going upstream was 75 minutes more than the time taken by him to cover the same distance going downstream. What was the time taken in hours by Hales to cover 20 kilometers going upstream? Assume the speed of the stream to be 4 kilometers per hour
a)
1.25
b)
1.6
c)
2.5
d)
5
e)
8

|
Sounak Iyer answered |
Given:
- Alex and Hales started rowing towards one another at constant speeds and met after rowing for an hour.
- The initial distance between Alex and Hales was 20 kilometers.
- Alex rowed downstream while Hales rowed upstream during this journey.
- The speed of the stream is 4 kilometers per hour.
- On some other day, the time taken by Alex alone, rowing at the same constant speed, to cover the distance between these two points going upstream was 75 minutes more than the time taken by him to cover the same distance going downstream.
To find: The time taken in hours by Hales to cover 20 kilometers going upstream.
Assumptions:
Let the speed of Alex be A, and the speed of Hales be H.
The speed of Alex downstream = A + 4
The speed of Alex upstream = A - 4
The speed of Hales upstream = H - 4
Calculation:
1. Let us assume that Alex covered x kilometers downstream in the first hour of rowing and Hales covered (20 - x) kilometers upstream.
2. As the speeds are constant, we can write the equation: x/(A + 4) = (20 - x)/(H - 4)
3. Solving this equation, we get x = (40H - 64A - 320)/(3H + 3A)
4. Now, the time taken by Alex to cover x kilometers downstream at a speed of (A + 4) is x/(A + 4) hours.
5. The time taken by Alex to cover (20 - x) kilometers upstream at a speed of (A - 4) is (20 - x)/(A - 4) hours.
6. As per the question, the time taken by Alex upstream is 75 minutes more than the time taken by Alex downstream. So we can write the equation: (20 - x)/(A - 4) = x/(A + 4) + 75/60
7. Substituting the value of x from step 3, we get (20 - (40H - 64A - 320)/(3H + 3A))/(A - 4) = (40H - 64A - 320)/(3H + 3A(A - 4)) + 5/4
8. Solving this equation, we get H = 5 km/hr
9. The time taken by Hales to cover 20 km upstream at a speed of (H - 4) is 20/(5 - 4) = 20 hours.
Therefore, the answer is option D) 5.
- Alex and Hales started rowing towards one another at constant speeds and met after rowing for an hour.
- The initial distance between Alex and Hales was 20 kilometers.
- Alex rowed downstream while Hales rowed upstream during this journey.
- The speed of the stream is 4 kilometers per hour.
- On some other day, the time taken by Alex alone, rowing at the same constant speed, to cover the distance between these two points going upstream was 75 minutes more than the time taken by him to cover the same distance going downstream.
To find: The time taken in hours by Hales to cover 20 kilometers going upstream.
Assumptions:
Let the speed of Alex be A, and the speed of Hales be H.
The speed of Alex downstream = A + 4
The speed of Alex upstream = A - 4
The speed of Hales upstream = H - 4
Calculation:
1. Let us assume that Alex covered x kilometers downstream in the first hour of rowing and Hales covered (20 - x) kilometers upstream.
2. As the speeds are constant, we can write the equation: x/(A + 4) = (20 - x)/(H - 4)
3. Solving this equation, we get x = (40H - 64A - 320)/(3H + 3A)
4. Now, the time taken by Alex to cover x kilometers downstream at a speed of (A + 4) is x/(A + 4) hours.
5. The time taken by Alex to cover (20 - x) kilometers upstream at a speed of (A - 4) is (20 - x)/(A - 4) hours.
6. As per the question, the time taken by Alex upstream is 75 minutes more than the time taken by Alex downstream. So we can write the equation: (20 - x)/(A - 4) = x/(A + 4) + 75/60
7. Substituting the value of x from step 3, we get (20 - (40H - 64A - 320)/(3H + 3A))/(A - 4) = (40H - 64A - 320)/(3H + 3A(A - 4)) + 5/4
8. Solving this equation, we get H = 5 km/hr
9. The time taken by Hales to cover 20 km upstream at a speed of (H - 4) is 20/(5 - 4) = 20 hours.
Therefore, the answer is option D) 5.
Alex and Brenda both stand at point X. Alex begins to walk away from Brenda in a straight line at a rate of 4 miles per hour. One hour later, Brenda begins to ride a bicycle in a straight line in the opposite direction at a rate of R miles per hour. If R > 8, which of the following represents the amount of time, in terms of R, that Alex will have been walking when Brenda has covered twice as much distance as Alex?- a)R – 4
- b)R / (R + 4)
- c)R / (R – 8)
- d)8 / (R – 8)
- e)R2 – 4
Correct answer is option 'C'. Can you explain this answer?
Alex and Brenda both stand at point X. Alex begins to walk away from Brenda in a straight line at a rate of 4 miles per hour. One hour later, Brenda begins to ride a bicycle in a straight line in the opposite direction at a rate of R miles per hour. If R > 8, which of the following represents the amount of time, in terms of R, that Alex will have been walking when Brenda has covered twice as much distance as Alex?
a)
R – 4
b)
R / (R + 4)
c)
R / (R – 8)
d)
8 / (R – 8)
e)
R2 – 4

|
Navya Yadav answered |
If we want Brenda's distance to be twice as great as Alex's distance, we can set up the following equation:
2(4T) = R(T – 1), where 4T is Alex's distance (rate × time) and R(T – 1) is Brenda's distance (since Brenda has been traveling for one hour less).
If we simplify this equation to isolate the T (which represents Alex's total time), we get:
2(4T) = R(T – 1)
8T = RT – R
R = RT – 8T
R = T(R – 8)
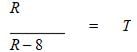
This is choice C
2(4T) = R(T – 1)
8T = RT – R
R = RT – 8T
R = T(R – 8)
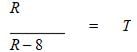
This is choice C
Riding her bicycle downhill, Sam reached the bottom of the 10-mile trail 10 minutes faster than it took her, riding 12 miles per hour, to reach the top of the trail. What was her downhill speed? - a)12 miles per hour
- b)15 miles per hour
- c)18 miles per hour
- d)21 miles per hour
- e)24 miles per hour
Correct answer is option 'B'. Can you explain this answer?
Riding her bicycle downhill, Sam reached the bottom of the 10-mile trail 10 minutes faster than it took her, riding 12 miles per hour, to reach the top of the trail. What was her downhill speed?
a)
12 miles per hour
b)
15 miles per hour
c)
18 miles per hour
d)
21 miles per hour
e)
24 miles per hour

|
Manasa Gupta answered |
Step 1: Question statement and Inferences
Riding 10 miles at her new speed took Sam 10 minutes less than riding the same distance at 12 miles per hour. What was this new speed?
Step 2: Finding required values
Start by finding the time it took Sam to reach the top of the hill.
Her uphill speed, u = 12 miles per hour
Distance travelled = 10 miles
Now considering the downhill journey, 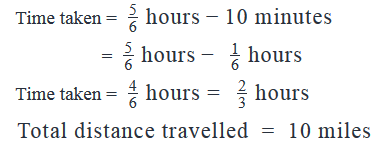
Step 3: Calculating the final answer
Answer: Option (B)
Triathlete Dan runs along a 2-mile stretch of river and then swims back along the same route. If Dan runs at a rate of 10 miles per hour and swims at a rate of 6 miles per hour, what is his average rate for the entire trip in miles per minute?- a)1/8
- b)2/15
- c)3/15
- d)1/4
- e)3/8
Correct answer is option 'A'. Can you explain this answer?
Triathlete Dan runs along a 2-mile stretch of river and then swims back along the same route. If Dan runs at a rate of 10 miles per hour and swims at a rate of 6 miles per hour, what is his average rate for the entire trip in miles per minute?
a)
1/8
b)
2/15
c)
3/15
d)
1/4
e)
3/8

|
Navya Yadav answered |
There is an important key to answering this question correctly: this is not a simple average problem but a weighted average problem. A weighted average is one in which the different parts to be averaged are not equally balanced. One is "worth more" than the other and skews the "simple" average in one direction. In addition, we must note a unit change in this problem: we are given rates in miles per hour but asked to solve for rates in miles per minute.
Average rate uses the same D = RT formula we use for rate problems but we have to figure out the different lengths of time it takes Dan to run and swim along the total 4-mile route. Then we have to take the 4 miles and divide by that total time. First, Dan runs 2 miles at the rate of 10 miles per hour. 10 miles per hour is equivalent to 1 mile every 6 minutes, so Dan takes 12 minutes to run the 2 miles. Next, Dan swims 2 miles at the rate of 6 miles per hour. 6 miles per hour is equivalent to 1 mile every 10 minutes, so Dan takes 20 minutes to swim the two miles.
Dan's total time is 12 + 20 = 32 minutes. Dan's total distance is 4 miles. Distance / time = 4 miles / 32 minutes = 1/8 miles per minute.
Note that if you do not weight the averages but merely take a simple average, you will get 2/15, which corresponds to incorrect answer choice B. 6 mph and 10 mph average to 8mph. (8mph)(1h/60min) = 8/60 miles/minute or 2/15 miles per minute.
The correct answer is A.
Average rate uses the same D = RT formula we use for rate problems but we have to figure out the different lengths of time it takes Dan to run and swim along the total 4-mile route. Then we have to take the 4 miles and divide by that total time. First, Dan runs 2 miles at the rate of 10 miles per hour. 10 miles per hour is equivalent to 1 mile every 6 minutes, so Dan takes 12 minutes to run the 2 miles. Next, Dan swims 2 miles at the rate of 6 miles per hour. 6 miles per hour is equivalent to 1 mile every 10 minutes, so Dan takes 20 minutes to swim the two miles.
Dan's total time is 12 + 20 = 32 minutes. Dan's total distance is 4 miles. Distance / time = 4 miles / 32 minutes = 1/8 miles per minute.
Note that if you do not weight the averages but merely take a simple average, you will get 2/15, which corresponds to incorrect answer choice B. 6 mph and 10 mph average to 8mph. (8mph)(1h/60min) = 8/60 miles/minute or 2/15 miles per minute.
The correct answer is A.
A man starts rowing from Point A in the direction of the water flow at a constant speed of 10 kilometers per hour. After rowing for 10 kilometers, he remembers that he forgot an important object at Point A and turns back to get it. After getting the object, he starts moving again in the direction of water flow, but due to an onset of exhaustion, he now rows at a constant speed of 8 kilometers per hour. After rowing for 26 kilometers, he reaches Point D, where he rests for 1 hour, and then resumes his journey in the same direction, rowing at a constant speed of 9 kilometers per hour, till he reaches Point B, which is 14 kilometers downstream from Point D. If the speed of water flow is 5 kilometers per hour, what is the average speed of the man for the entire journey?- a)9 kilometers per hour
- b)130/17 kilometers per hour
- c)120/17 kilometers per hour
- d)20/3 kilometers per hour
- e)6 kilometers per hour
Correct answer is option 'A'. Can you explain this answer?
A man starts rowing from Point A in the direction of the water flow at a constant speed of 10 kilometers per hour. After rowing for 10 kilometers, he remembers that he forgot an important object at Point A and turns back to get it. After getting the object, he starts moving again in the direction of water flow, but due to an onset of exhaustion, he now rows at a constant speed of 8 kilometers per hour. After rowing for 26 kilometers, he reaches Point D, where he rests for 1 hour, and then resumes his journey in the same direction, rowing at a constant speed of 9 kilometers per hour, till he reaches Point B, which is 14 kilometers downstream from Point D. If the speed of water flow is 5 kilometers per hour, what is the average speed of the man for the entire journey?
a)
9 kilometers per hour
b)
130/17 kilometers per hour
c)
120/17 kilometers per hour
d)
20/3 kilometers per hour
e)
6 kilometers per hour

|
Abhishek Choudhury answered |
Problem Solving Approach:
- Break down the journey into different parts and calculate the time taken for each part.
- Use the time and distance information to calculate the average speed of the entire journey.
Calculation:
- Let's assume the distance between A and D is x kilometers.
- The speed of the water flow is 5 km/hr, so the effective speed of the man while rowing in the direction of water flow is 10 + 5 = 15 km/hr, and while rowing against the water flow is 8 - 5 = 3 km/hr.
- Time taken to row from A to D = distance/speed = x/15 hours
- Time taken to row from D to B = distance/speed = 14/9 hours
- Time taken for rest at D = 1 hour
- Time taken for the round trip from A to D and back to D = (10/15) + (10/3) = 2.33 hours
- Total distance covered in the journey = 10 + x + 26 + 14 = x + 50 kilometers
- Total time taken for the journey = x/15 + 2.33 + 26/8 + 14/9 + 1 = x/15 + 6.8 hours
- Average speed of the journey = total distance covered/total time taken = (x + 50)/(x/15 + 6.8) kilometers per hour
- To find the value of x, we can use the fact that the time taken for the round trip from A to D and back to D is the same as the time taken to row from A to D.
- (10/15) + (10/3) = x/15
- x = 20 kilometers
- Substituting x = 20 in the average speed formula, we get:
- Average speed = (20 + 50)/(20/15 + 6.8) = 9 kilometers per hour
Therefore, the correct answer is option A, 9 kilometers per hour.
- Break down the journey into different parts and calculate the time taken for each part.
- Use the time and distance information to calculate the average speed of the entire journey.
Calculation:
- Let's assume the distance between A and D is x kilometers.
- The speed of the water flow is 5 km/hr, so the effective speed of the man while rowing in the direction of water flow is 10 + 5 = 15 km/hr, and while rowing against the water flow is 8 - 5 = 3 km/hr.
- Time taken to row from A to D = distance/speed = x/15 hours
- Time taken to row from D to B = distance/speed = 14/9 hours
- Time taken for rest at D = 1 hour
- Time taken for the round trip from A to D and back to D = (10/15) + (10/3) = 2.33 hours
- Total distance covered in the journey = 10 + x + 26 + 14 = x + 50 kilometers
- Total time taken for the journey = x/15 + 2.33 + 26/8 + 14/9 + 1 = x/15 + 6.8 hours
- Average speed of the journey = total distance covered/total time taken = (x + 50)/(x/15 + 6.8) kilometers per hour
- To find the value of x, we can use the fact that the time taken for the round trip from A to D and back to D is the same as the time taken to row from A to D.
- (10/15) + (10/3) = x/15
- x = 20 kilometers
- Substituting x = 20 in the average speed formula, we get:
- Average speed = (20 + 50)/(20/15 + 6.8) = 9 kilometers per hour
Therefore, the correct answer is option A, 9 kilometers per hour.
A thief was spotted by a policeman from a distance of 225 metres. When the policeman started the chase, the thief also started running. If the speed of the thief was 11 km/h and that of the policeman was 13 km/h, how far would the thief have run, before the policeman caught up with him ?- a)1237.5 metres
- b)1137.5 metres
- c)1357.5 metres
- d)1256.5 metres
- e)1298.5 metres
Correct answer is option 'A'. Can you explain this answer?
A thief was spotted by a policeman from a distance of 225 metres. When the policeman started the chase, the thief also started running. If the speed of the thief was 11 km/h and that of the policeman was 13 km/h, how far would the thief have run, before the policeman caught up with him ?
a)
1237.5 metres
b)
1137.5 metres
c)
1357.5 metres
d)
1256.5 metres
e)
1298.5 metres

|
EduRev GMAT answered |

Deb normally drives to work in 45 minutes at an average speed of 40 miles per hour. This week, however, she plans to bike to work along a route that decreases the total distance she usually travels when driving by 20% . If Deb averages between 12 and 16 miles per hour when biking, how many minutes earlier will she need to leave in the morning in order to ensure she arrives at work at the same time as when she drives?- a)135
- b)105
- c)95
- d)75
- e)45
Correct answer is option 'D'. Can you explain this answer?
Deb normally drives to work in 45 minutes at an average speed of 40 miles per hour. This week, however, she plans to bike to work along a route that decreases the total distance she usually travels when driving by 20% . If Deb averages between 12 and 16 miles per hour when biking, how many minutes earlier will she need to leave in the morning in order to ensure she arrives at work at the same time as when she drives?
a)
135
b)
105
c)
95
d)
75
e)
45

|
Pallabi Sengupta answered |
This standard rate problem will rely heavily on the formula RT=D, where R is the rate, T is the time and D is the distance traveled.
First, we should find the driving and biking distances:
If Deb drives for 45 minutes, or 0.75 hours, at a rate of 40mph, she drives a total distance of
(0.75)(40) = 30 miles.
If the bike route is 20% shorter than the driving route, the bike route is 30 – 30(0.2) = 30 – 6 = 24 miles.
Next, we need to determine how long it will take Deb to travel the route by bike. She wants to ensure that she'll get to work by a particular time, so we want to calculate the longest possible time it could take her; therefore, we have to assume she will bike at the slowest end of the range of the speeds given: 12mph. If she travels 24 miles at 12mph, it will take her 24/12 = 2 hours or 120 minutes.
If Deb normally takes 45 minutes to drive to work but could take up to 120 minutes to bike to work, then she must leave 120 – 45 = 75 minutes earlier than she normally does to ensure that she will arrive at work at the same time.
The correct answer is D.
First, we should find the driving and biking distances:
If Deb drives for 45 minutes, or 0.75 hours, at a rate of 40mph, she drives a total distance of
(0.75)(40) = 30 miles.
If the bike route is 20% shorter than the driving route, the bike route is 30 – 30(0.2) = 30 – 6 = 24 miles.
Next, we need to determine how long it will take Deb to travel the route by bike. She wants to ensure that she'll get to work by a particular time, so we want to calculate the longest possible time it could take her; therefore, we have to assume she will bike at the slowest end of the range of the speeds given: 12mph. If she travels 24 miles at 12mph, it will take her 24/12 = 2 hours or 120 minutes.
If Deb normally takes 45 minutes to drive to work but could take up to 120 minutes to bike to work, then she must leave 120 – 45 = 75 minutes earlier than she normally does to ensure that she will arrive at work at the same time.
The correct answer is D.
A boat travels from Point A to Point B in the direction of water and then returns to Point A. In still water, the boat travels at a
speed of 28 kilometres per hour. If the speed of the water current is 4 kilometres per hour and the time taken for the round-trip is 2
hours and 55 minutes, what is the total distance travelled by the boat in the round trip?- a)40 kilometres
- b)71 kilometres
- c)80 kilometres
- d)82 kilometres
- e)86 kilometres
Correct answer is option 'C'. Can you explain this answer?
A boat travels from Point A to Point B in the direction of water and then returns to Point A. In still water, the boat travels at a
speed of 28 kilometres per hour. If the speed of the water current is 4 kilometres per hour and the time taken for the round-trip is 2
hours and 55 minutes, what is the total distance travelled by the boat in the round trip?
speed of 28 kilometres per hour. If the speed of the water current is 4 kilometres per hour and the time taken for the round-trip is 2
hours and 55 minutes, what is the total distance travelled by the boat in the round trip?
a)
40 kilometres
b)
71 kilometres
c)
80 kilometres
d)
82 kilometres
e)
86 kilometres

|
Pranav Kulkarni answered |
Given data:
Speed of the boat in still water = 28 km/h
Speed of the water current = 4 km/h
Total time taken for the round trip = 2 hours 55 minutes = 2.92 hours
Let the distance between point A and point B be d km.
Speed of the boat downstream = (28 + 4) km/h = 32 km/h
Speed of the boat upstream = (28 - 4) km/h = 24 km/h
Let the time taken by the boat to travel from A to B (downstream) be t1 hours.
Then, the time taken by the boat to travel from B to A (upstream) will be (2.92 - t1) hours.
Using the formula, distance = speed × time, we can write:
Distance downstream = 32t1 km
Distance upstream = 24(2.92 - t1) km
Total distance travelled by the boat in the round trip = Distance downstream + Distance upstream
= 32t1 + 24(2.92 - t1) km
= 32t1 + 70.08 - 24t1 km
= 8t1 + 70.08 km
Now, we need to find the value of t1.
Using the formula, distance = speed × time, we can write:
d = 28t1 + 4t1 (distance = speed downstream × time downstream)
=> d = 32t1
=> t1 = d/32
Substituting the value of t1 in the expression for total distance, we get:
Total distance travelled by the boat in the round trip = 8(d/32) + 70.08 km
= 0.25d + 70.08 km
We need to find the value of d.
Total time taken for the round trip = time downstream + time upstream
=> 2.92 = t1 + (2.92 - t1)
=> 2.92 = 2 × 2.92 - t1
=> t1 = 2.92 - 1.46 = 1.46 hours
Substituting the value of t1 in the expression for distance, we get:
d = 28 × 1.46 + 4 × 1.46 = 40.88 km
Substituting the value of d in the expression for total distance, we get:
Total distance travelled by the boat in the round trip = 0.25 × 40.88 + 70.08 km
= 10.22 + 70.08 km
= 80.3 km (approx.)
Hence, the correct option is (c) 80 km.
Speed of the boat in still water = 28 km/h
Speed of the water current = 4 km/h
Total time taken for the round trip = 2 hours 55 minutes = 2.92 hours
Let the distance between point A and point B be d km.
Speed of the boat downstream = (28 + 4) km/h = 32 km/h
Speed of the boat upstream = (28 - 4) km/h = 24 km/h
Let the time taken by the boat to travel from A to B (downstream) be t1 hours.
Then, the time taken by the boat to travel from B to A (upstream) will be (2.92 - t1) hours.
Using the formula, distance = speed × time, we can write:
Distance downstream = 32t1 km
Distance upstream = 24(2.92 - t1) km
Total distance travelled by the boat in the round trip = Distance downstream + Distance upstream
= 32t1 + 24(2.92 - t1) km
= 32t1 + 70.08 - 24t1 km
= 8t1 + 70.08 km
Now, we need to find the value of t1.
Using the formula, distance = speed × time, we can write:
d = 28t1 + 4t1 (distance = speed downstream × time downstream)
=> d = 32t1
=> t1 = d/32
Substituting the value of t1 in the expression for total distance, we get:
Total distance travelled by the boat in the round trip = 8(d/32) + 70.08 km
= 0.25d + 70.08 km
We need to find the value of d.
Total time taken for the round trip = time downstream + time upstream
=> 2.92 = t1 + (2.92 - t1)
=> 2.92 = 2 × 2.92 - t1
=> t1 = 2.92 - 1.46 = 1.46 hours
Substituting the value of t1 in the expression for distance, we get:
d = 28 × 1.46 + 4 × 1.46 = 40.88 km
Substituting the value of d in the expression for total distance, we get:
Total distance travelled by the boat in the round trip = 0.25 × 40.88 + 70.08 km
= 10.22 + 70.08 km
= 80.3 km (approx.)
Hence, the correct option is (c) 80 km.
The ‘moving walkway’ is a 300-foot long conveyor belt that moves continuously at 3 feet per second. When Bill steps on the walkway, a group of people that are also on the walkway stands 120 feet in front of him. He walks toward the group at a combined rate (including both walkway and foot speed) of 6 feet per second, reaches the group of people, and then remains stationary until the walkway ends. What is Bill’s average rate of movement for his trip along the moving walkway?- a)2 feet per second
- b)2.5 feet per second
- c)3 feet per second
- d)4 feet per second
- e)5 feet per second
Correct answer is option 'E'. Can you explain this answer?
The ‘moving walkway’ is a 300-foot long conveyor belt that moves continuously at 3 feet per second. When Bill steps on the walkway, a group of people that are also on the walkway stands 120 feet in front of him. He walks toward the group at a combined rate (including both walkway and foot speed) of 6 feet per second, reaches the group of people, and then remains stationary until the walkway ends. What is Bill’s average rate of movement for his trip along the moving walkway?
a)
2 feet per second
b)
2.5 feet per second
c)
3 feet per second
d)
4 feet per second
e)
5 feet per second

|
Navya Yadav answered |
To determine Bill’s average rate of movement, first recall that Rate × Time = Distance. We are given that the moving walkway is 300 feet long, so we need only determine the time elapsed during Bill’s journey to determine his average rate.
There are two ways to find the time of Bill’s journey. First, we can break down Bill’s journey into two legs: walking and standing. While walking, Bill moves at 6 feet per second. Because the walkway moves at 3 feet per second, Bill’s foot speed along the walkway is 6 – 3 = 3 feet per second. Therefore, he covers the 120 feet between himself and the bottleneck in (120 feet)/(3 feet per second) = 40 seconds.
There are two ways to find the time of Bill’s journey. First, we can break down Bill’s journey into two legs: walking and standing. While walking, Bill moves at 6 feet per second. Because the walkway moves at 3 feet per second, Bill’s foot speed along the walkway is 6 – 3 = 3 feet per second. Therefore, he covers the 120 feet between himself and the bottleneck in (120 feet)/(3 feet per second) = 40 seconds.
Now, how far along is Bill when he stops walking? While that 40 seconds elapsed, the crowd would have moved (40 seconds)(3 feet per second) = 120 feet. Because the crowd already had a 120 foot head start, Bill catches up to them at 120 + 120 = 240 feet. The final 60 feet are covered at the rate of the moving walkway, 3 feet per second, and therefore require (60 feet)/(3 feet per second) = 20 seconds. The total journey requires 40 + 20 = 60 seconds, and Bill’s rate of movement is (300 feet)/(60 seconds) = 5 feet per second.
This problem may also be solved with a shortcut. Consider that Bill’s journey will end when the crowd reaches the end of the walkway (as long as he catches up with the crowd before the walkway ends). When he steps on the walkway, the crowd is 180 feet from the end. The walkway travels this distance in (180 feet)/(3 feet per second) = 60 seconds, and Bill’s average rate of movement is (300 feet)/(60 seconds) = 5 feet per second.
The correct answer is E.
Megan and David start running along the perimeter of a square park. To make one round of the park, Megan takes 1 minute and
David takes 1 minute and 36 seconds. If both Megan and David burn 24 calories in making one round of the park, in how much
time will Megan have burnt 120 calories more than David?- a)8 minutes 40 seconds
- b)13 minutes 20 seconds
- c)18 minutes 54 seconds
- d)19 minutes 30 seconds
- e)A unique value cannot be determined
Correct answer is option 'B'. Can you explain this answer?
Megan and David start running along the perimeter of a square park. To make one round of the park, Megan takes 1 minute and
David takes 1 minute and 36 seconds. If both Megan and David burn 24 calories in making one round of the park, in how much
time will Megan have burnt 120 calories more than David?
David takes 1 minute and 36 seconds. If both Megan and David burn 24 calories in making one round of the park, in how much
time will Megan have burnt 120 calories more than David?
a)
8 minutes 40 seconds
b)
13 minutes 20 seconds
c)
18 minutes 54 seconds
d)
19 minutes 30 seconds
e)
A unique value cannot be determined

|
Saumya Sharma answered |
Given:
- Megan takes 1 minute and David takes 1 minute and 36 seconds to make one round of the park.
- Both Megan and David burn 24 calories in making one round of the park.
- Megan needs to burn 120 calories more than David.
To find: In how much time Megan will burn 120 calories more than David.
Approach:
- Calculate the number of calories burnt by Megan and David per minute.
- Calculate the difference in calories burnt per minute by Megan and David.
- Divide the required additional calories burned by Megan by the difference calculated above to get the time taken by Megan to burn 120 calories more than David.
Calculation:
- Megan takes 1 minute to burn 24 calories, so she burns 24 calories/minute.
- David takes 1 minute and 36 seconds to burn 24 calories, so he burns 24 calories/(1 minute and 36 seconds) = 15 calories/minute.
- The difference in calories burnt per minute by Megan and David = 24 - 15 = 9 calories/minute.
- To burn 120 calories more, Megan needs to burn 24 + 120 = 144 calories in total.
- Time taken by Megan to burn 120 calories more = 120 calories/9 calories/minute = 13 minutes and 20 seconds.
Therefore, the correct answer is option (b) 13 minutes 20 seconds.
- Megan takes 1 minute and David takes 1 minute and 36 seconds to make one round of the park.
- Both Megan and David burn 24 calories in making one round of the park.
- Megan needs to burn 120 calories more than David.
To find: In how much time Megan will burn 120 calories more than David.
Approach:
- Calculate the number of calories burnt by Megan and David per minute.
- Calculate the difference in calories burnt per minute by Megan and David.
- Divide the required additional calories burned by Megan by the difference calculated above to get the time taken by Megan to burn 120 calories more than David.
Calculation:
- Megan takes 1 minute to burn 24 calories, so she burns 24 calories/minute.
- David takes 1 minute and 36 seconds to burn 24 calories, so he burns 24 calories/(1 minute and 36 seconds) = 15 calories/minute.
- The difference in calories burnt per minute by Megan and David = 24 - 15 = 9 calories/minute.
- To burn 120 calories more, Megan needs to burn 24 + 120 = 144 calories in total.
- Time taken by Megan to burn 120 calories more = 120 calories/9 calories/minute = 13 minutes and 20 seconds.
Therefore, the correct answer is option (b) 13 minutes 20 seconds.
On a Monday, John left from his home for his office at 09:05 AM and reached his office at 10:00 AM. On Tuesday, he left from his home for his office 15 minutes later than the time he left his home on Monday and reached his office 4 minutes later than the time he reached his office on Monday. If on Tuesday, John drove at an average speed that was 15 kilometres per hour faster than his average speed on Monday, how far in kilometres was his office from his home?- a)50
- b)55
- c)60
- d)65
- e)75
Correct answer is option 'B'. Can you explain this answer?
On a Monday, John left from his home for his office at 09:05 AM and reached his office at 10:00 AM. On Tuesday, he left from his home for his office 15 minutes later than the time he left his home on Monday and reached his office 4 minutes later than the time he reached his office on Monday. If on Tuesday, John drove at an average speed that was 15 kilometres per hour faster than his average speed on Monday, how far in kilometres was his office from his home?
a)
50
b)
55
c)
60
d)
65
e)
75

|
Sahana Mehta answered |
Given:
John left for his office at 09:05 AM and reached his office at 10:00 AM on Monday.
On Tuesday, he left for his office 15 minutes later than the time he left his home on Monday and reached his office 4 minutes later than the time he reached his office on Monday.
On Tuesday, John drove at an average speed that was 15 kilometres per hour faster than his average speed on Monday.
To find:
The distance in kilometers between John's home and office.
Solution:
Let's first calculate the time taken by John to reach his office on Monday.
Time taken on Monday = 10:00 AM - 09:05 AM = 55 minutes
Now, let's calculate the time taken by John on Tuesday.
Time taken on Tuesday = Time taken on Monday + 4 minutes = 55 + 4 = 59 minutes
John left 15 minutes later on Tuesday than he did on Monday. So, he left on Tuesday at 09:20 AM.
Now, let's calculate John's average speed on Monday.
Average speed on Monday = Distance/Time taken on Monday
Let's assume the distance between John's home and office to be 'd' kilometers.
So, the average speed on Monday = d/55
On Tuesday, John drove at an average speed that was 15 kilometers per hour faster than his average speed on Monday.
Average speed on Tuesday = Average speed on Monday + 15
= d/55 + 15
Now, let's calculate the distance between John's home and office.
Distance = Average speed on Tuesday x Time taken on Tuesday
= (d/55 + 15) x 59
Equating the above equation with 'd', we get:
d = 55 x 15 = 825
Therefore, the distance between John's home and office is 825 kilometers.
Hence, the correct answer is option (B).
John left for his office at 09:05 AM and reached his office at 10:00 AM on Monday.
On Tuesday, he left for his office 15 minutes later than the time he left his home on Monday and reached his office 4 minutes later than the time he reached his office on Monday.
On Tuesday, John drove at an average speed that was 15 kilometres per hour faster than his average speed on Monday.
To find:
The distance in kilometers between John's home and office.
Solution:
Let's first calculate the time taken by John to reach his office on Monday.
Time taken on Monday = 10:00 AM - 09:05 AM = 55 minutes
Now, let's calculate the time taken by John on Tuesday.
Time taken on Tuesday = Time taken on Monday + 4 minutes = 55 + 4 = 59 minutes
John left 15 minutes later on Tuesday than he did on Monday. So, he left on Tuesday at 09:20 AM.
Now, let's calculate John's average speed on Monday.
Average speed on Monday = Distance/Time taken on Monday
Let's assume the distance between John's home and office to be 'd' kilometers.
So, the average speed on Monday = d/55
On Tuesday, John drove at an average speed that was 15 kilometers per hour faster than his average speed on Monday.
Average speed on Tuesday = Average speed on Monday + 15
= d/55 + 15
Now, let's calculate the distance between John's home and office.
Distance = Average speed on Tuesday x Time taken on Tuesday
= (d/55 + 15) x 59
Equating the above equation with 'd', we get:
d = 55 x 15 = 825
Therefore, the distance between John's home and office is 825 kilometers.
Hence, the correct answer is option (B).
An international flight takes off from New Delhi in India for Washington DC in the United States of America via Doha, where the flight stops for 2 hours and 40 minutes. During flight, the average speed of the plane is 660 kilometres per hour and the flight reaches Washington DC, at 3:50 PM, Washington time. If the distance between New Delhi and Washington DC via Doha is 12000 kilometres and New Delhi is 9 hour 30 minutes ahead of Washington DC, what is the approximate time in New Delhi when the flight takes off from there?- a)12:30 AM
- b)4:30 AM
- c)7:10 AM
- d)12:10 PM
- e)7:30 PM
Correct answer is option 'B'. Can you explain this answer?
An international flight takes off from New Delhi in India for Washington DC in the United States of America via Doha, where the flight stops for 2 hours and 40 minutes. During flight, the average speed of the plane is 660 kilometres per hour and the flight reaches Washington DC, at 3:50 PM, Washington time. If the distance between New Delhi and Washington DC via Doha is 12000 kilometres and New Delhi is 9 hour 30 minutes ahead of Washington DC, what is the approximate time in New Delhi when the flight takes off from there?
a)
12:30 AM
b)
4:30 AM
c)
7:10 AM
d)
12:10 PM
e)
7:30 PM

|
Palak Saha answered |
Given information:
- Distance between New Delhi and Washington DC via Doha: 12000 kilometers
- Average speed of the plane: 660 kilometers per hour
- Flight reaches Washington DC at 3:50 PM, Washington time
- New Delhi is 9 hours and 30 minutes ahead of Washington DC
To find: The approximate time in New Delhi when the flight takes off from there.
Let's break down the problem step by step:
1. Calculate the flight duration from New Delhi to Washington DC via Doha:
- Flight distance: 12000 kilometers
- Average speed of the plane: 660 kilometers per hour
- Flight duration = Distance / Speed = 12000 / 660 = 18.18 hours
2. Calculate the local time in Washington DC when the flight reaches there:
- Given time: 3:50 PM, Washington time
- The flight duration is 18.18 hours, so subtracting this from the given time:
3:50 PM - 18 hours = 9:50 AM, Washington time
- However, we need to consider the time difference between New Delhi and Washington DC.
3. Calculate the time difference between New Delhi and Washington DC:
- New Delhi is 9 hours and 30 minutes ahead of Washington DC.
- Subtracting this time difference from the Washington time:
9:50 AM - 9 hours 30 minutes = 12:20 AM, New Delhi time
4. Adjust the time for the layover in Doha:
- The flight stops in Doha for 2 hours and 40 minutes.
- Adding this layover time to the calculated New Delhi time:
12:20 AM + 2 hours 40 minutes = 2:00 AM, New Delhi time
Therefore, the approximate time in New Delhi when the flight takes off from there is 2:00 AM, which corresponds to option B.
- Distance between New Delhi and Washington DC via Doha: 12000 kilometers
- Average speed of the plane: 660 kilometers per hour
- Flight reaches Washington DC at 3:50 PM, Washington time
- New Delhi is 9 hours and 30 minutes ahead of Washington DC
To find: The approximate time in New Delhi when the flight takes off from there.
Let's break down the problem step by step:
1. Calculate the flight duration from New Delhi to Washington DC via Doha:
- Flight distance: 12000 kilometers
- Average speed of the plane: 660 kilometers per hour
- Flight duration = Distance / Speed = 12000 / 660 = 18.18 hours
2. Calculate the local time in Washington DC when the flight reaches there:
- Given time: 3:50 PM, Washington time
- The flight duration is 18.18 hours, so subtracting this from the given time:
3:50 PM - 18 hours = 9:50 AM, Washington time
- However, we need to consider the time difference between New Delhi and Washington DC.
3. Calculate the time difference between New Delhi and Washington DC:
- New Delhi is 9 hours and 30 minutes ahead of Washington DC.
- Subtracting this time difference from the Washington time:
9:50 AM - 9 hours 30 minutes = 12:20 AM, New Delhi time
4. Adjust the time for the layover in Doha:
- The flight stops in Doha for 2 hours and 40 minutes.
- Adding this layover time to the calculated New Delhi time:
12:20 AM + 2 hours 40 minutes = 2:00 AM, New Delhi time
Therefore, the approximate time in New Delhi when the flight takes off from there is 2:00 AM, which corresponds to option B.
Rachel drove at a constant speed from inn A along a highway to inn B. Did Rachel reach inn B from inn A in less than an hour?
(1) If Rachel had driven to inn C that was 15 kilometers further down the highway, she would have taken 50% more time
(2) If Rachel’s average speed for the drive had been 20 kilometers per hour lesser, she would have taken 50% more time
- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
- b)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
- c)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
- d)EACH statement ALONE is sufficient to answer the question
asked.
- e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'B'. Can you explain this answer?
Rachel drove at a constant speed from inn A along a highway to inn B. Did Rachel reach inn B from inn A in less than an hour?
(1) If Rachel had driven to inn C that was 15 kilometers further down the highway, she would have taken 50% more time
(2) If Rachel’s average speed for the drive had been 20 kilometers per hour lesser, she would have taken 50% more time
(2) If Rachel’s average speed for the drive had been 20 kilometers per hour lesser, she would have taken 50% more time
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
c)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.

|
Niharika Sen answered |
Step 1 & 2: Understand Question and Draw Inference
Let distance between Inns A and B = D kilometers (km in short)
Let Rachel’s average speed = S kilometers per hour (kmph in short)
So, Time taken by Rachel to travel from A to B = D/S hours.
Let Rachel’s average speed = S kilometers per hour (kmph in short)
So, Time taken by Rachel to travel from A to B = D/S hours.
To Find: Is D/S < 1 ?
To answer the question, we need to know the value of ratio D/S
Step 3 : Analyze Statement 1 independent
Statement 1 says that: 'If Rachel had driven to inn C that was 15 kilometers further down the highway, she would have taken 50% more time’
So, not sufficient.
Step 4 : Analyze Statement 2 independent
Statement 2 says that: ‘If Rachel’s average speed for the drive had been 20 kilometers per hour lesser, she would have taken 50% more time’
Step 5: Analyze Both Statements Together (if needed)
From Statement 1: D = 30 km
From Statement 2: S = 60 kmph
Sufficient to find a unique value of the ratio D/S
From Statement 2: S = 60 kmph
Sufficient to find a unique value of the ratio D/S
Answer: Option C
Johnny drove with an average speed of m miles per hour for h hours, increased his average speed to m + s miles per hour for an additional h hour and then increased his average speed to twice the original speed for a final h hours. Which of the following represents the distance which he drove? - a)h(2m +s)
- b)h(4m +s)
- c)h(m2 +s)
- d)h2(m +s)
- e)h(m +s)2
Correct answer is option 'B'. Can you explain this answer?
Johnny drove with an average speed of m miles per hour for h hours, increased his average speed to m + s miles per hour for an additional h hour and then increased his average speed to twice the original speed for a final h hours. Which of the following represents the distance which he drove?
a)
h(2m +s)
b)
h(4m +s)
c)
h(m2 +s)
d)
h2(m +s)
e)
h(m +s)2
|
|
Tanker Dharti answered |
Thank you
 The table above shows the minimum and the maximum running speeds of two animals. If Animal A runs between two poles that
The table above shows the minimum and the maximum running speeds of two animals. If Animal A runs between two poles that
are placed 20 metres apart in 3 seconds and Animal B runs between the same poles in 4 seconds, which of the following
cannot be the value of X?I. 23
II. 26
III. 27- a)I only
- b)II only
- c)III only
- d)I, II and III
- e)None of the above
Correct answer is option 'D'. Can you explain this answer?
The table above shows the minimum and the maximum running speeds of two animals. If Animal A runs between two poles that
are placed 20 metres apart in 3 seconds and Animal B runs between the same poles in 4 seconds, which of the following
cannot be the value of X?
are placed 20 metres apart in 3 seconds and Animal B runs between the same poles in 4 seconds, which of the following
cannot be the value of X?
I. 23
II. 26
III. 27
II. 26
III. 27
a)
I only
b)
II only
c)
III only
d)
I, II and III
e)
None of the above
|
|
Adithi Roy Chowdhury answered |
For animal A = 20/3 = 6.67m/sec =x. Now for animal B, similarly speed = 20/4 = 5 m/sec = x and none of these are in the options ... So option D is the correct answer
Patrick takes 2 hours to drive in his car from point A to point B. What is the distance between A and B?(1) If his average speed for the journey had been 20 kilometers per hour greater, he would have taken only 1 hour and 36 minutes to reach point B(2) Patrick covered an average of 800 meters every 36 seconds- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
Patrick takes 2 hours to drive in his car from point A to point B. What is the distance between A and B?
(1) If his average speed for the journey had been 20 kilometers per hour greater, he would have taken only 1 hour and 36 minutes to reach point B
(2) Patrick covered an average of 800 meters every 36 seconds
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked
not sufficient to answer the question asked
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed.
answer the question asked, and additional data specific to the problem are needed.

|
Srestha Basu answered |
Given information:
Patrick takes 2 hours to drive in his car from point A to point B.
To find:
The distance between A and B.
Statement 1:
If his average speed for the journey had been 20 kilometers per hour greater, he would have taken only 1 hour and 36 minutes to reach point B.
This statement provides information about the time and the speed of the journey. We can use this information to calculate the distance.
Let the distance between A and B be d km.
According to the given information, the time taken by Patrick to travel from A to B at his original speed is 2 hours. Therefore, his original speed is d/2 km/h.
If his speed had been 20 km/h greater, his new speed would be (d/2)+20 km/h.
According to statement 1, the time taken by Patrick to travel from A to B at his new speed is 1 hour and 36 minutes, which is equal to 1.6 hours.
Therefore, we can form the following equation:
d/(d/2+20) = 1.6
Solving this equation, we get d = 96 km.
Therefore, statement 1 alone is sufficient to answer the question.
Statement 2:
Patrick covered an average of 800 meters every 36 seconds.
This statement provides information about the speed of Patrick but does not provide any information about the time taken or the distance traveled.
Therefore, statement 2 alone is not sufficient to answer the question.
Combined:
Using both statements 1 and 2, we have already calculated the distance between A and B as 96 km. Therefore, both statements together are sufficient to answer the question.
Hence, the correct answer is option D.
Patrick takes 2 hours to drive in his car from point A to point B.
To find:
The distance between A and B.
Statement 1:
If his average speed for the journey had been 20 kilometers per hour greater, he would have taken only 1 hour and 36 minutes to reach point B.
This statement provides information about the time and the speed of the journey. We can use this information to calculate the distance.
Let the distance between A and B be d km.
According to the given information, the time taken by Patrick to travel from A to B at his original speed is 2 hours. Therefore, his original speed is d/2 km/h.
If his speed had been 20 km/h greater, his new speed would be (d/2)+20 km/h.
According to statement 1, the time taken by Patrick to travel from A to B at his new speed is 1 hour and 36 minutes, which is equal to 1.6 hours.
Therefore, we can form the following equation:
d/(d/2+20) = 1.6
Solving this equation, we get d = 96 km.
Therefore, statement 1 alone is sufficient to answer the question.
Statement 2:
Patrick covered an average of 800 meters every 36 seconds.
This statement provides information about the speed of Patrick but does not provide any information about the time taken or the distance traveled.
Therefore, statement 2 alone is not sufficient to answer the question.
Combined:
Using both statements 1 and 2, we have already calculated the distance between A and B as 96 km. Therefore, both statements together are sufficient to answer the question.
Hence, the correct answer is option D.
On a trip of 60 kilometres, Rita covered the first 15 kilometres at an average speed of 75 kilometres per hour and the following 35 kilometres at an average speed of 140 kilometres per hour. At what average speed did she cover the last part of her trip if her average speed for the whole trip was 80 kilometres per hour?- a)3 kilometres per hour
- b)25 kilometres per hour
- c)30 kilometres per hour
- d)100/3 kilometres per hour
- e)200/3 kilometres per hour
Correct answer is option 'D'. Can you explain this answer?
On a trip of 60 kilometres, Rita covered the first 15 kilometres at an average speed of 75 kilometres per hour and the following 35 kilometres at an average speed of 140 kilometres per hour. At what average speed did she cover the last part of her trip if her average speed for the whole trip was 80 kilometres per hour?
a)
3 kilometres per hour
b)
25 kilometres per hour
c)
30 kilometres per hour
d)
100/3 kilometres per hour
e)
200/3 kilometres per hour

|
Sharmila Nambiar answered |
Given:
- The Whole Trip:
- Total distance = 60 km
- The Average Speed for the whole trip = 80 kmph
- Part 1 of Trip:
- Distance = 15 km
- Average Speed = 75 kmph
- Part 2 of Trip:
- Distance = 35 km
- Average Speed = 140 kmph
- The Last Part of Trip:
- Distance = 60 – (15 + 35) = 60 – 50 = 10 km
To Find: Average Speed for The Last Part of Trip
Approach:
2. So, to answer the question, we need to find Time Taken for Last Part of Trip:
Working out:
- Finding Time taken for Last Part of Trip:
Looking at the answer choices, we see that the correct answer is Option D
At 11 AM, Abraham leaves from his home for a meeting that is scheduled for 1 PM. If the venue of the meeting is not less than 100 kilometers away and Abraham drives at a speed not less than 60 kilometers per hour, will he be late for the meeting?(1) The venue of the meeting is less than 120 kilometers away(2) He does not drive at a speed greater than 80 kilometers per hour- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'A'. Can you explain this answer?
At 11 AM, Abraham leaves from his home for a meeting that is scheduled for 1 PM. If the venue of the meeting is not less than 100 kilometers away and Abraham drives at a speed not less than 60 kilometers per hour, will he be late for the meeting?
(1) The venue of the meeting is less than 120 kilometers away
(2) He does not drive at a speed greater than 80 kilometers per hour
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed.
answer the question asked, and additional data specific to the problem are needed.

|
Kiran Nambiar answered |
Question Analysis:
The question asks whether Abraham will be late for the meeting or not, given that he leaves at 11 AM, the meeting is scheduled for 1 PM, the venue is not less than 100 km away, and he drives at a speed not less than 60 km/h. The two statements provide information about the distance of the meeting venue and the maximum speed at which Abraham can drive.
Statement Analysis:
Statement 1: The venue of the meeting is less than 120 kilometers away.
This statement tells us the upper limit of the distance that Abraham needs to travel. If the distance is less than 120 km, then Abraham will have enough time to reach the venue before 1 PM, even if he drives at the minimum speed of 60 km/h. Hence, this statement alone is sufficient to answer the question.
Statement 2: He does not drive at a speed greater than 80 kilometers per hour.
This statement provides the upper limit of the speed at which Abraham can drive. However, it does not give any information about the distance of the meeting venue. Therefore, this statement alone is not sufficient to answer the question.
Combining Statements 1 and 2:
By combining the two statements, we know that the distance of the meeting venue is between 100 km (minimum distance given in the question stem) and 120 km (maximum distance given in Statement 1). We also know that Abraham does not drive at a speed greater than 80 km/h. However, we do not know his actual driving speed, which could be anywhere between 60 km/h and 80 km/h. Therefore, the combined statements are not sufficient to answer the question.
Answer:
The correct answer is (A) Statement (1) alone is sufficient, but statement (2) alone is not sufficient to answer the question asked.
The question asks whether Abraham will be late for the meeting or not, given that he leaves at 11 AM, the meeting is scheduled for 1 PM, the venue is not less than 100 km away, and he drives at a speed not less than 60 km/h. The two statements provide information about the distance of the meeting venue and the maximum speed at which Abraham can drive.
Statement Analysis:
Statement 1: The venue of the meeting is less than 120 kilometers away.
This statement tells us the upper limit of the distance that Abraham needs to travel. If the distance is less than 120 km, then Abraham will have enough time to reach the venue before 1 PM, even if he drives at the minimum speed of 60 km/h. Hence, this statement alone is sufficient to answer the question.
Statement 2: He does not drive at a speed greater than 80 kilometers per hour.
This statement provides the upper limit of the speed at which Abraham can drive. However, it does not give any information about the distance of the meeting venue. Therefore, this statement alone is not sufficient to answer the question.
Combining Statements 1 and 2:
By combining the two statements, we know that the distance of the meeting venue is between 100 km (minimum distance given in the question stem) and 120 km (maximum distance given in Statement 1). We also know that Abraham does not drive at a speed greater than 80 km/h. However, we do not know his actual driving speed, which could be anywhere between 60 km/h and 80 km/h. Therefore, the combined statements are not sufficient to answer the question.
Answer:
The correct answer is (A) Statement (1) alone is sufficient, but statement (2) alone is not sufficient to answer the question asked.
John leaves from his home at 10 AM and starts driving towards a city that is 300 kilometres away, at a constant speed of 50 miles
per hour. His brother Martin leaves the home at 11:30 AM and starts driving on the same route at a constant speed of 60 miles
per hour. If they stop driving once they reach the city, which of the following statements must be true? (1 mile = 1.6 kilometres)
I. John reaches the city before Martin
II. At 1:30 PM, John is 55 kilometres ahead of Martin
III. Martin overtake John at 4 PM- a)I only
- b)II only
- c)III only
- d)I and II only
- e)II and III only
Correct answer is option 'A'. Can you explain this answer?
John leaves from his home at 10 AM and starts driving towards a city that is 300 kilometres away, at a constant speed of 50 miles
per hour. His brother Martin leaves the home at 11:30 AM and starts driving on the same route at a constant speed of 60 miles
per hour. If they stop driving once they reach the city, which of the following statements must be true? (1 mile = 1.6 kilometres)
I. John reaches the city before Martin
II. At 1:30 PM, John is 55 kilometres ahead of Martin
III. Martin overtake John at 4 PM
per hour. His brother Martin leaves the home at 11:30 AM and starts driving on the same route at a constant speed of 60 miles
per hour. If they stop driving once they reach the city, which of the following statements must be true? (1 mile = 1.6 kilometres)
I. John reaches the city before Martin
II. At 1:30 PM, John is 55 kilometres ahead of Martin
III. Martin overtake John at 4 PM
a)
I only
b)
II only
c)
III only
d)
I and II only
e)
II and III only

|
Maya Khanna answered |
Given:
- Home – City distance = 300 km
- John:
- Speed = 50 miles per hour (Note that the distance is given in kilometers and John’s speed is given in miles per hour)
- 1 mile = 1.6 kilometers
- Time of start= 10 AM
- Speed = 50 miles per hour (Note that the distance is given in kilometers and John’s speed is given in miles per hour)
- Martin:
- Speed = 60 miles per hour
- Time of start = 11:30 AM
To Find: Which of the 3 statements must be true?
Approach:
1. We will evaluate the 3 statements one by one
Working out:
- Evaluating Statement I
- To evaluate this statement, we need to find the time at which John reaches the city and the time at which Martin reaches the city
- John:
- Speed = 50 miles per hour = 50*1.6 kilometers per hour
- So, time (hours) =
- John starts at 10 AM
- So, John reaches the city at 10 AM + 3 hours 45 min = 1:45 PM
- Martin:
- Speed = 60 miles per hour = 60*1.6 kilometers per hour
- So, time (hours) =
- Martin starts at 11:30 AM
- So, Martin reaches the city at 11:30 AM + 3 hours 7.5 min = 2: (37.5) PM
- Therefore, Statement I is indeed true
- Evaluating Statement II
- At 1:30 PM, John has been travelling for (1:30 PM – 10 AM =) 3.5 hours and Martin for (1:30 PM – 11:30 AM =) 2 hours
- So, distance between them at 1:30 PM = 280 – 192 = 88 km
- Therefore, Statement II is not true
- Evaluating Statement III
- In our analysis of Statement I, we’ve already seen that John reached the city before Martin. Since both of them stop driving once they reach the city, Martin never manages to overtake John (and none of them are still driving at 4 PM)
- Therefore, Statement III is not true.
- Getting to the answer
- Thus, we see that out of the 3 statements, only Statement I is true.
Looking at the answer choices, we see that the correct answer is Option A
John and Jacob set out together on bicycle traveling at 15 and 12 miles per hour, respectively. After 40
minutes, John stops to fix a flat tire. If it takes John one hour to fix the flat tire and Jacob continues to ride during this time, how many hours will it take John to catch up to Jacob assuming he resumes his ride at 15 miles per hour? (consider John's deceleration/acceleration before/after the flat to be negligible)- a)3
- b)3.33
- c)
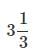
- d)4
- e)
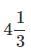
Correct answer is option 'B'. Can you explain this answer?
John and Jacob set out together on bicycle traveling at 15 and 12 miles per hour, respectively. After 40
minutes, John stops to fix a flat tire. If it takes John one hour to fix the flat tire and Jacob continues to ride during this time, how many hours will it take John to catch up to Jacob assuming he resumes his ride at 15 miles per hour? (consider John's deceleration/acceleration before/after the flat to be negligible)
minutes, John stops to fix a flat tire. If it takes John one hour to fix the flat tire and Jacob continues to ride during this time, how many hours will it take John to catch up to Jacob assuming he resumes his ride at 15 miles per hour? (consider John's deceleration/acceleration before/after the flat to be negligible)
a)
3
b)
3.33
c)
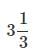
d)
4
e)
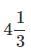

|
Navya Yadav answered |
It is easier to break this motion up into different segments. Let's first consider the 40 minutes up until John stops to fix his flat.
40 minutes is 2/3 of an hour.
In 2/3 of an hour, John traveled 15 × 2/3 = 10 miles (rt = d)
In that same 2/3 of an hour, Jacob traveled 12 × 2/3 = 8 miles
John therefore had a two-mile lead when he stopped to fix his tire.
In 2/3 of an hour, John traveled 15 × 2/3 = 10 miles (rt = d)
In that same 2/3 of an hour, Jacob traveled 12 × 2/3 = 8 miles
John therefore had a two-mile lead when he stopped to fix his tire.
It took John 1 hour to fix his tire, during which time Jacob traveled 12 miles. Since John began this 1-hour period 2 miles ahead, at the end of the period he is 12 – 2 = 10 miles behind Jacob.
The question now becomes "how long does it take John to bridge the 10-mile gap between him and Jacob, plus whatever additional distance Jacob has covered, while traveling at 15 miles per hour while Jacob is traveling at 12 miles per hour?" We can set up an rt = d chart to solve this.
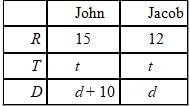
The question now becomes "how long does it take John to bridge the 10-mile gap between him and Jacob, plus whatever additional distance Jacob has covered, while traveling at 15 miles per hour while Jacob is traveling at 12 miles per hour?" We can set up an rt = d chart to solve this.

John's travel during this "catch-up period" can be represented as 15t = d + 10
Jacob's travel during this "catch-up period" can be represented as 12t = d
Jacob's travel during this "catch-up period" can be represented as 12t = d
If we solve these two simultaneous equations, we get:
15t = 12t + 10
3t = 10
t = 3 1/3 hours
Another way to approach this question is to note that when John begins to ride again, Jacob is 10 miles ahead. So John must make up those first 10 miles plus whatever additional distance Jacob has covered while both are riding. Since Jacob's additional distance at any given moment is 12t (measuring from the moment when John begins riding again) we can represent the distance that John has to make up as 12t + 10. We can also represent John's distance at any given moment as 15t. Therefore, 15t = 12t + 10, when John catches up to Jacob. We can solve this question as outlined above.
15t = 12t + 10
3t = 10
t = 3 1/3 hours
Another way to approach this question is to note that when John begins to ride again, Jacob is 10 miles ahead. So John must make up those first 10 miles plus whatever additional distance Jacob has covered while both are riding. Since Jacob's additional distance at any given moment is 12t (measuring from the moment when John begins riding again) we can represent the distance that John has to make up as 12t + 10. We can also represent John's distance at any given moment as 15t. Therefore, 15t = 12t + 10, when John catches up to Jacob. We can solve this question as outlined above.
The correct answer is B.
A man rows at the rate of 5 mph in still water. If the river runs at the rate of 1 mph, it takes him 1 hour to row to a place and come back. What is the total distance covered by him in miles?- a)2
- b)2.4
- c)2.8
- d)4
- e)4.8
Correct answer is option 'E'. Can you explain this answer?
A man rows at the rate of 5 mph in still water. If the river runs at the rate of 1 mph, it takes him 1 hour to row to a place and come back. What is the total distance covered by him in miles?
a)
2
b)
2.4
c)
2.8
d)
4
e)
4.8

|
EduRev GMAT answered |
Correct Answer :- e
Explanation : Speed downstream = (5 + 1) kmph = 6 mph.
Speed upstream = (5 - 1) kmph = 4 mph.
Let the required distance be x m.
Then, x/6 + x/4 = 1
2x + 3x = 12
5x = 12
x = 2.4
Therefore, the total distance covered is 2 * 2.4 = 4.8 miles.
Had Frank driven at an averagespeed of 40 miles per hour, he would have reached his office 10 minutes earlier than he usually
did. At what average speed should Frank drive to reach his office 20 minutes earlier than he usually did?
(1) Frank usually takes 5/6 hours to reach his office
(2) The distance to his office is 80/3 miles- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed.
Correct answer is option 'D'. Can you explain this answer?
Had Frank driven at an averagespeed of 40 miles per hour, he would have reached his office 10 minutes earlier than he usually
did. At what average speed should Frank drive to reach his office 20 minutes earlier than he usually did?
(1) Frank usually takes 5/6 hours to reach his office
(2) The distance to his office is 80/3 miles
did. At what average speed should Frank drive to reach his office 20 minutes earlier than he usually did?
(1) Frank usually takes 5/6 hours to reach his office
(2) The distance to his office is 80/3 miles
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the problem are needed.
answer the question asked, and additional data specific to the problem are needed.

|
Sharmila Nambiar answered |
Step 1 & 2: Understand Question and Draw Inference
Given:
- Let Frank’s usual time to reach his office be t hours
- So, when speed of Frank = 40 miles per hour, he takes (
) hours to reach his office
- Distance to Frank’s office = 40 * (
) miles
To Find: Speed of Frank so that he takes (  ) hours to reach his office
) hours to reach his office
- Let the speed of Frank be S miles per hour
- Hence, Distance covered by Frank driving at S miles per hour for(
) hours = S*(
)miles
- Now, we know that distance to Frank’s office = 40 * (
) miles
- So,we can write S*(
) = 40 * (
)
- Hence, to find the value of S, we need to find the value of t.
Step 3 : Analyze Statement 1 independent
Statement-1: Frank usually takes 5/6 hours to reach his office
- We are given that t = 5/6 hours. So, we can find the value of S
Statement-1 is sufficient to answer the question
Step 4 : Analyze Statement 2 independent
Statement-2: The distance to his office is 80/3 miles
- We know that disatance to Frank’s office is 40 * (
)
- So, we can write 40 * (
) = 80/3 miles .
- As it is a linear equation in t, we can find the value of t
- Once we know the value of t. we can find the value of S
Statement-2 is sufficient to answer the question.
Step 5: Analyze Both Statements Together (if needed)
As we have unique answer from steps 3 and 4 above, this step is not required.
Answer: D
It takes the high-speed train x hours to travel the z miles from Town A to Town B at a constant rate, while it takes the regular train y hours to travel the same distance at a constant rate. If the high-speed train leaves Town A for Town B at the same time that the regular train leaves Town B for Town A, how many more miles will the high-speed train have traveled than the regular train when the two trains pass each other?- a)
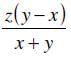
- b)
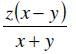
- c)
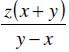
- d)
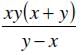
- e)

Correct answer is option 'A'. Can you explain this answer?
It takes the high-speed train x hours to travel the z miles from Town A to Town B at a constant rate, while it takes the regular train y hours to travel the same distance at a constant rate. If the high-speed train leaves Town A for Town B at the same time that the regular train leaves Town B for Town A, how many more miles will the high-speed train have traveled than the regular train when the two trains pass each other?
a)
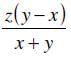
b)
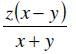
c)
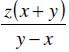
d)
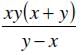
e)


|
Sharmila Singh answered |
A question with variables in the answer choices (VIC) can be solved by picking values for the variables.
Let's pick the following values for x, y and z:

When picking values for a VIC question, it is best to pick numbers that are easy to work with (i.e., 12 is divisible by 4 and 6 here), but that don't have any extraneous relationships between them. For example x = 4, y = 3, z = 12 would be a less favorable set of numbers because xy would equal z in that case and there is no need for the product of the two times to equal the distance. Picking variables with extraneous relationships can lead to false positives when checking the answer choices.
Let's pick the following values for x, y and z:

When picking values for a VIC question, it is best to pick numbers that are easy to work with (i.e., 12 is divisible by 4 and 6 here), but that don't have any extraneous relationships between them. For example x = 4, y = 3, z = 12 would be a less favorable set of numbers because xy would equal z in that case and there is no need for the product of the two times to equal the distance. Picking variables with extraneous relationships can lead to false positives when checking the answer choices.
Now let's solve the question according to the values we selected.
If the high-speed train travels the 12 miles from A to B in 4 hours, it is traveling at 3 mph.
If the regular train travels the 12 miles from A to B in 6 hours, it is traveling at 2 mph.
If the high-speed train travels the 12 miles from A to B in 4 hours, it is traveling at 3 mph.
If the regular train travels the 12 miles from A to B in 6 hours, it is traveling at 2 mph.
To evaluate how far each train travels when they move toward each other starting at opposite ends, let's set up an RTD chart.
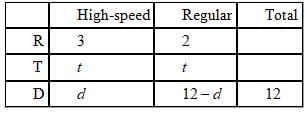
We can set-up two equations with two unknowns and solve

We can set-up two equations with two unknowns and solve
In the 2.4 hours it takes for the two trains to meet,
the high speed train will have traveled 3(2.4) = 7.2 miles,
and the regular train will have traveled 2(2.4) = 4.8 miles.
Therefore the high speed train will have traveled 7.2 – 4.8 = 2.4 miles farther than the regular train.
2.4 is our target number.
the high speed train will have traveled 3(2.4) = 7.2 miles,
and the regular train will have traveled 2(2.4) = 4.8 miles.
Therefore the high speed train will have traveled 7.2 – 4.8 = 2.4 miles farther than the regular train.
2.4 is our target number.
Let's see which of the five answer choices give us 2.4 when we plug in our values for x, y and z:
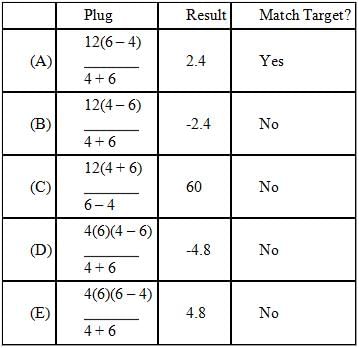

Only A matches the target.
This question can also be solved algebraically.
Since the trains traveled the z miles in x and y hours, their speeds can be represented as z/x and z/y respectively.
Since the trains traveled the z miles in x and y hours, their speeds can be represented as z/x and z/y respectively.
We can again use an RTD chart to evaluate how far each train travels when they move toward each other starting at opposite ends. Instead of using another variable d here, let's express the two distances in terms of their respective rates and times.
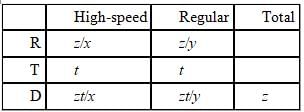

Since the two distances sum to the total when the two trains meet, we can set up the following equation:
zt/x + zt/y = z - divide both sides of the equation by z
t/x + t/y = 1 - multiply both sides of the equation by xy
ty + tx = xy - factor out a t on the left side
t(x + y) = xy - divide both sides by x + y
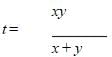
t/x + t/y = 1 - multiply both sides of the equation by xy
ty + tx = xy - factor out a t on the left side
t(x + y) = xy - divide both sides by x + y
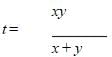
To find how much further the high-speed train went in this time:
(ratehigh × time) – (ratereg × time)
(ratehigh – ratereg) × time
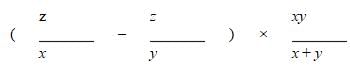
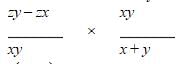
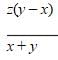
The correct answer is A.
(ratehigh × time) – (ratereg × time)
(ratehigh – ratereg) × time
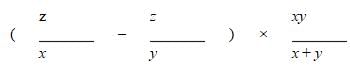
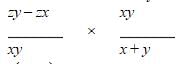
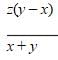
The correct answer is A.
Raymond travelled from city A to city C via city B. Was his average speed for the journey from city A to city B greater than his average speed for the journey from city B to city C?(1) Raymond’s average speed of the journey from city A to city B was greater than his average speed of the journey from city A to city C.(2) Had Raymond travelled at a constant speed from city A to city C, the time taken by him to travel from city A to city B would have been lesser than the time taken by him to travel from city B to city C.- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked. - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked. - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed
Correct answer is option 'A'. Can you explain this answer?
Raymond travelled from city A to city C via city B. Was his average speed for the journey from city A to city B greater than his average speed for the journey from city B to city C?
(1) Raymond’s average speed of the journey from city A to city B was greater than his average speed of the journey from city A to city C.
(2) Had Raymond travelled at a constant speed from city A to city C, the time taken by him to travel from city A to city B would have been lesser than the time taken by him to travel from city B to city C.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked
not sufficient to answer the question asked
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked.
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed
answer the question asked, and additional data specific to the
problem are needed

|
Ankita Chauhan answered |
Step 1 & 2: Understand Question and Draw Inference
Step 3 : Analyze Statement 1 independent
(1) Raymond’s average speed of the journey from city A to city B was greater than his average speed of the journey from city A to city C.
As the denominators of the inequalities are positive, we can multiply and solve it to get
Sufficient to answer.
Step 4 : Analyze Statement 2 independent
(2) Had Raymond travelled at a constant speed from city A to city C, the time taken by him to travel from city A to city B would have been lesser than the time taken by him to travel from city B to city C.
Let Raymond’s constant speed be S kilometeres per hour
Let Raymond’s constant speed be S kilometeres per hour
It does not tell us anything about the average speeds of Raymomd from city A to city B and city B to city C. Insufficient to answer
Step 5: Analyze Both Statements Together (if needed)
Since, we have a unique answer from step 3, this step is not required.
Answer: A
Answer: A
Brian drives a certain part of his journey at an average speed of 30 miles per hour and the rest at an average speed of 60 miles per hour. If he drives for 100 miles, is his average speed for the journey greater than 45 miles per hour?(1) Brian drives for 30 miles per hour for twice the time than he drives for 60 miles per hour.(2) Had Brian driven at an average speed of 40 miles per hour rather than 30 miles per hour, his average speed for the
journey would have been 48 miles per hour.- a)Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked. - b)Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked - c)BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked - d)EACH statement ALONE is sufficient to answer the question
asked. - e)Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
Correct answer is option 'D'. Can you explain this answer?
Brian drives a certain part of his journey at an average speed of 30 miles per hour and the rest at an average speed of 60 miles per hour. If he drives for 100 miles, is his average speed for the journey greater than 45 miles per hour?
(1) Brian drives for 30 miles per hour for twice the time than he drives for 60 miles per hour.
(2) Had Brian driven at an average speed of 40 miles per hour rather than 30 miles per hour, his average speed for the
journey would have been 48 miles per hour.
journey would have been 48 miles per hour.
a)
Statement (1) ALONE is sufficient, but statement (2) alone is
not sufficient to answer the question asked.
not sufficient to answer the question asked.
b)
Statement (2) ALONE is sufficient, but statement (1) alone is
not sufficient to answer the question asked
not sufficient to answer the question asked
c)
BOTH statements (1) and (2) TOGETHER are sufficient to
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked
answer the question asked, but NEITHER statement ALONE
is sufficient to answer the question asked
d)
EACH statement ALONE is sufficient to answer the question
asked.
asked.
e)
Statements (1) and (2) TOGETHER are NOT sufficient to
answer the question asked, and additional data specific to the
problem are needed.
answer the question asked, and additional data specific to the
problem are needed.

|
Tanvi Deshpande answered |
Step 1 & 2: Understand Question and Draw Inference
- Let the distance for which he drives for 30 miles per hour be x miles.
- Distance for which he drives for 60 miles per hour = 100 – x miles
Step 3 : Analyze Statement 1 independent
(1) Brian drives for 30 miles per hour for twice the time than he drives for 60 miles per hour.
As we know the values of x, we can find if 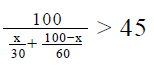
Sufficient to answer
Step 4 : Analyze Statement 2 independent
(2) Had Brian driven at an average speed of 40 miles per hour rather than 30 miles per hour, his average speed for the journey would have been 48 miles per hour.
As we know the values of x, we can find if 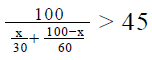
Sufficient to answer.
Step 5: Analyze Both Statements Together (if needed)
Since, we have a unique answers from steps 3 and 4, this step is not needed.
Answer: D
Answer: D
Chapter doubts & questions for Time, Speed and Distance - Quantitative for GMAT 2025 is part of GMAT exam preparation. The chapters have been prepared according to the GMAT exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for GMAT 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Time, Speed and Distance - Quantitative for GMAT in English & Hindi are available as part of GMAT exam.
Download more important topics, notes, lectures and mock test series for GMAT Exam by signing up for free.
Quantitative for GMAT
127 videos|154 docs|111 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup









