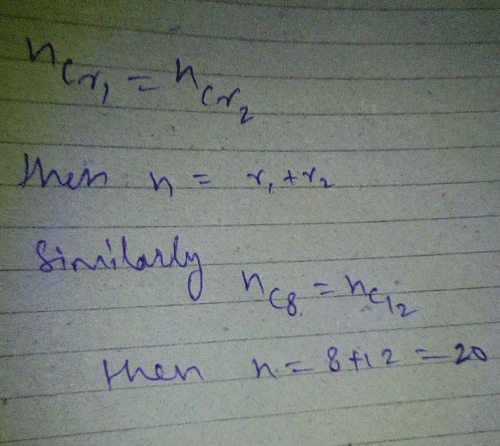All Exams >
Commerce >
Online MCQ Tests for Commerce >
All Questions
All questions of Binomial Theorem for Commerce Exam
A lady wants to select one cotton saree and one polyster saree from a textile shop. If there are 15 cotton and 13 polyster varieties in that shop, in how many ways can she pick up two sarees?- a)125
- b)215
- c)345
- d)195
Correct answer is option 'D'. Can you explain this answer?
A lady wants to select one cotton saree and one polyster saree from a textile shop. If there are 15 cotton and 13 polyster varieties in that shop, in how many ways can she pick up two sarees?
a)
125
b)
215
c)
345
d)
195
|
Suresh Reddy answered |
The lady can select one cotton saree out of 15 cotton varieties in 15 ways since
any of 15 varieties can be selected. Corresponding to each selection of a cotton saree, she can
choose a polyester saree in 13 ways. Hence the two sarees (one cotton and one polyester), by
multiplication principle of counting, can be selected in 15 x 13= 195 ways
any of 15 varieties can be selected. Corresponding to each selection of a cotton saree, she can
choose a polyester saree in 13 ways. Hence the two sarees (one cotton and one polyester), by
multiplication principle of counting, can be selected in 15 x 13= 195 ways
The number of ways in which the 6 faces of a cube can be painted with 6 different colours is- a)6
- b)12
- c)6!
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
The number of ways in which the 6 faces of a cube can be painted with 6 different colours is
a)
6
b)
12
c)
6!
d)
none of these
|
Preeti Iyer answered |
Consider the face that has red color. There are five face
Four alphabets A, M, P, O are purchased from a warehouse. How many ordered pairs of initials can be formed using these?- a)10
- b)16
- c)18
- d)12
Correct answer is option 'D'. Can you explain this answer?
Four alphabets A, M, P, O are purchased from a warehouse. How many ordered pairs of initials can be formed using these?
a)
10
b)
16
c)
18
d)
12
|
Riya Banerjee answered |
Total number of letters = 4
Number of ordered pairs of letters that can be formed like (A, M) or (P, O) etc = 4P2 = 4!/2!
= 24/2
= 12
Number of ordered pairs of letters that can be formed like (A, M) or (P, O) etc = 4P2 = 4!/2!
= 24/2
= 12
In how many ways can a cricket team of 11 players be chosen out from a squad of 14 players, if 5 particular players are always chosen?- a)84
- b)144
- c)1001
- d)1365
Correct answer is option 'A'. Can you explain this answer?
In how many ways can a cricket team of 11 players be chosen out from a squad of 14 players, if 5 particular players are always chosen?
a)
84
b)
144
c)
1001
d)
1365
|
Aryan Khanna answered |
Total no of players = 14 out of which 5 are fixed.
So, 11-5 = 6
Remaining players = 14 - 6
= 9 players
9C6 = 9!/(3!*6!)
= 84
So, 11-5 = 6
Remaining players = 14 - 6
= 9 players
9C6 = 9!/(3!*6!)
= 84
How many three digit odd numbers can be formed by using the digits 5,6,7,8 if the repetition of digits is allowed?- a)64
- b)32
- c)24
- d)None of these
Correct answer is 'B'. Can you explain this answer?
How many three digit odd numbers can be formed by using the digits 5,6,7,8 if the repetition of digits is allowed?
a)
64
b)
32
c)
24
d)
None of these
|
|
Pooja Shah answered |
The unit place can be filled in 2 ways because question asked to find 3 digit odd numbers from 5,6,7,8 and the other two places can be filled in 4 ways as repetition is allowed.
So, Unit's place can be filled in 2 ways. Decimal place can be filled in 4 ways. Hundred's place can be filled in 4 ways.
=> 4*4*2 = 32.
So, Unit's place can be filled in 2 ways. Decimal place can be filled in 4 ways. Hundred's place can be filled in 4 ways.
=> 4*4*2 = 32.
In how many ways can 3 letters be posted in 4 letter boxes?- a)27
- b)4!
- c)64
- d)3!
Correct answer is option 'C'. Can you explain this answer?
In how many ways can 3 letters be posted in 4 letter boxes?
a)
27
b)
4!
c)
64
d)
3!
|
|
Preeti Iyer answered |
The first letter can be posted in 4 ways. So, total outcomes about the first letter = 4.
For every outcome about the first letter, the second letter can be posted in 4 ways. So, total outcomes about the first and the second letters= (4*4) = 16.
Therefore, following the same route, we can say, total possible outcomes about the first and the second letters = (4*4*4) = 64.
In how many ways 2 directors and 3 executives can be arranged for a meeting? If there are 6 chairs available two on one side and remaining four on the other side of the table and the two directors has to be together on one side and the executives on the other side.- a)24
- b)48
- c)720
- d)120
Correct answer is option 'B'. Can you explain this answer?
In how many ways 2 directors and 3 executives can be arranged for a meeting? If there are 6 chairs available two on one side and remaining four on the other side of the table and the two directors has to be together on one side and the executives on the other side.
a)
24
b)
48
c)
720
d)
120
|
Hansa Sharma answered |
3 executives in 4 chairs = 4P3 ways
Total no. of ways = 2! * 4P3
=> 2*1*(4!/1!)
= 2*24
= 48
Total no. of ways = 2! * 4P3
=> 2*1*(4!/1!)
= 2*24
= 48
How many three digit odd numbers can be formed by using the digits 1,2,3,4,5,6 if the repetition of digit is not allowed:- a)216
- b)120
- c)60
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
How many three digit odd numbers can be formed by using the digits 1,2,3,4,5,6 if the repetition of digit is not allowed:
a)
216
b)
120
c)
60
d)
None of these
|
Lavanya Menon answered |
There can be only 3 digits at the last digit (1,3,5) the middle digit should have 5 No's. out of 6, because one digit is used in last digit similarly 1st digit will have 4 No's.
Therefore : 4×5×3 => 60
In how many ways can a cricket team be selected out of 15 players if a particular player has to be included?- a)C(14,11)
- b)C(14,10)
- c)C(15,11)
- d)C(15,10)
Correct answer is option 'A'. Can you explain this answer?
In how many ways can a cricket team be selected out of 15 players if a particular player has to be included?
a)
C(14,11)
b)
C(14,10)
c)
C(15,11)
d)
C(15,10)
|
|
Pooja Shah answered |
11 players can be selected out of 16 in 16C11 ways = 16!/(11! 5!) = 4368 ways. Now, If two particular players is to be included and one particular player is to be rejected, then we have to select 9 more players out of 13 in 13C9 ways.
= 13!/(9! 4!) = 715 ways.
= 13!/(9! 4!) = 715 ways.
?
How many numbers are there between 100 and 1000 , in which all the digits are distinct?- a)729
- b)648
- c)858
- d)546
Correct answer is option 'B'. Can you explain this answer?
How many numbers are there between 100 and 1000 , in which all the digits are distinct?
a)
729
b)
648
c)
858
d)
546
|
Nandini Patel answered |
H T U
9.9.8 = 9 x 9 x 8 = 648 numbers
No. of digits in hundreds place should be filled first as the zero should be excluded
(1,2,3,4,5,6,7,8,9) = 9 ways
No. of digits in tens place (now the zero can be included but one digit has been used at hundreds place) so, no. of ways we can fill ten's place is = 9 ways
No of digits in units place is any one among the remaining 8 no. = 8 ways
so, 9 x 9 x 8 = 648
The number of different ways in which a man can invite one or more of his 6 friends to dinner is?- a)30
- b)63
- c)120
- d)15
Correct answer is option 'B'. Can you explain this answer?
The number of different ways in which a man can invite one or more of his 6 friends to dinner is?
a)
30
b)
63
c)
120
d)
15
|
Infinity Academy answered |
He can invite any one friend in 6C1 ways = 6 ways:
He can invite any two friends in 6C2 ways = 15 ways
He can invite any three friends in 6C3 ways = 20 ways
He can invite any 4 friends in 6C4ways = 15 ways
He can invite any 5 friends in 6C5 ways = 6 ways
He can invite all the 6 friends in 6C6 ways= 1 way.
Since any one of these could happen total possibilities are, 6+15+20+15+6+1 = 63.
He can invite any two friends in 6C2 ways = 15 ways
He can invite any three friends in 6C3 ways = 20 ways
He can invite any 4 friends in 6C4ways = 15 ways
He can invite any 5 friends in 6C5 ways = 6 ways
He can invite all the 6 friends in 6C6 ways= 1 way.
Since any one of these could happen total possibilities are, 6+15+20+15+6+1 = 63.
A room has 8 doors. In how many ways, a man can enter in the room through one door and exit through a different door?- a)5040
- b)40320
- c)56
- d)8
Correct answer is option 'C'. Can you explain this answer?
A room has 8 doors. In how many ways, a man can enter in the room through one door and exit through a different door?
a)
5040
b)
40320
c)
56
d)
8
|
|
Naina Sharma answered |
The person has 8 options to enter the hall. For each of these 8 options, he has 7 options to exit the hall. Thus, he has 8 × 7 = 56 ways to enter and exit from different doors.
There are 7 chairs in a row. In how many ways can 3 persons occupy any three of them- a)240
- b)210
- c)260
- d)120
Correct answer is option 'B'. Can you explain this answer?
There are 7 chairs in a row. In how many ways can 3 persons occupy any three of them
a)
240
b)
210
c)
260
d)
120
|
|
Neha Joshi answered |
First person can sit on any of the 7 seats, second person can sit on other 6 vacant seats except one occupied by the first one. Similarly, the third can do sit on 5 so, total no. of ways = 7*6*5 = 210
How many triangles can be formed by joining four points on a circle?- a)8
- b)6
- c)4
- d)2
Correct answer is option 'C'. Can you explain this answer?
How many triangles can be formed by joining four points on a circle?
a)
8
b)
6
c)
4
d)
2
|
|
Preeti Khanna answered |
Triangle formed = mC3
Therefore, 4 points on circle, m = 4
4C3 = 4C1
⇒ 4
Therefore, 4 points on circle, m = 4
4C3 = 4C1
⇒ 4
Nidhi has 6 friends. In how many ways can she invite one or more of them to a party at her home?- a)64
- b)63
- c)25
- d)24
Correct answer is option 'B'. Can you explain this answer?
Nidhi has 6 friends. In how many ways can she invite one or more of them to a party at her home?
a)
64
b)
63
c)
25
d)
24
|
|
Lavanya Menon answered |
She has 6 friends and he wants to invite one or more. That is the same as saying he wants to invite at least 1 of his friends.
So, the number of ways he could do this is:
Invite only one friend
Invite any two friends
Invite any three friends
Invite any four friends
Invite any five friends
Invite all six friends
This can be thought of in terms of combinations. Inviting r friends out of n is same as choosing r friends out of n . So, we can write the possibilities as:
6C1 + 6C2 + 6C3 + 6C4 + 6C5 + 6C6
= 6 + 15 + 20 + 15 + 6 + 1
= 63
So, the number of ways he could do this is:
Invite only one friend
Invite any two friends
Invite any three friends
Invite any four friends
Invite any five friends
Invite all six friends
This can be thought of in terms of combinations. Inviting r friends out of n is same as choosing r friends out of n . So, we can write the possibilities as:
6C1 + 6C2 + 6C3 + 6C4 + 6C5 + 6C6
= 6 + 15 + 20 + 15 + 6 + 1
= 63
A lady arranges a dinner party for 6 guests .The number of ways in which they may be selected from among 10 friends if 2 of the friends will not attend the party together is- a)164
- b)140
- c)112
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
A lady arranges a dinner party for 6 guests .The number of ways in which they may be selected from among 10 friends if 2 of the friends will not attend the party together is
a)
164
b)
140
c)
112
d)
none of these
|
|
Neha Joshi answered |
Let us say that the two particular friends are A and B.
If A is invited among six guests and B is not, then: number of combinations to select 5 more guests from the remaining 8 friends:
C(8, 5) = 8 ! / (5! 3!) = 56
If B is invited among the six guests and A is not , then the number of ways of selecting the remaining 5 guests = C(8, 5) = 56
Suppose both A and B are not included in the six guests list : then the number of such combinations = C(8, 6) = 7 * 8 /2 = 28
So the total number of sets of guests that can be selected = 140.
If A is invited among six guests and B is not, then: number of combinations to select 5 more guests from the remaining 8 friends:
C(8, 5) = 8 ! / (5! 3!) = 56
If B is invited among the six guests and A is not , then the number of ways of selecting the remaining 5 guests = C(8, 5) = 56
Suppose both A and B are not included in the six guests list : then the number of such combinations = C(8, 6) = 7 * 8 /2 = 28
So the total number of sets of guests that can be selected = 140.
The number of ways in which 6 “ + “ and 4 “ – “ signs can be arranged in a line such that no two “ – “ signs occur together is- a)P(10,4)
- b)C(7,4)
- c)C(10,4)
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The number of ways in which 6 “ + “ and 4 “ – “ signs can be arranged in a line such that no two “ – “ signs occur together is
a)
P(10,4)
b)
C(7,4)
c)
C(10,4)
d)
none of these
|
Sushil Kumar answered |
′+′ signs can be put in a row in one way creating seven gaps shown as arrows:
Now 4′−′ signs must be kept in these gaps. So, no tow ′−′ signs should be together.
Out of these 7 gaps 4 can be chosen in 7C4 ways.
Now 4′−′ signs must be kept in these gaps. So, no tow ′−′ signs should be together.
Out of these 7 gaps 4 can be chosen in 7C4 ways.
Number of signals that can be made using given 4 flags of which 3 are blue and 1 is red?- a)3i
- b)12
- c)4i
- d)4
Correct answer is option 'D'. Can you explain this answer?
Number of signals that can be made using given 4 flags of which 3 are blue and 1 is red?
a)
3i
b)
12
c)
4i
d)
4
|
Shiksha Academy answered |
Total flags = 4
Blue = 3
red = 1
Total no. of signals = (4!*3!)/3!
= 4
Blue = 3
red = 1
Total no. of signals = (4!*3!)/3!
= 4
How many number of four digits can be formed with the digits 1,2,3,4,5 if the digit can be repeated in any number of times?- a)55
- b)5!
- c)625
- d)9000
Correct answer is option 'C'. Can you explain this answer?
How many number of four digits can be formed with the digits 1,2,3,4,5 if the digit can be repeated in any number of times?
a)
55
b)
5!
c)
625
d)
9000
|
Om Desai answered |
There are 5 digits 1,2,3,4 & 5. the 4 digit number can be formed with the digits 1,2,3,4,5 where digits can be repeated =5*5*5*5=625.
The total number of ways of answering 5 objective questions, each question having four choices are- a)2880
- b)120
- c)1024
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
The total number of ways of answering 5 objective questions, each question having four choices are
a)
2880
b)
120
c)
1024
d)
None of the above
|
|
Preeti Iyer answered |
The total ways of answering would be. 4x4x4x4x4=4^5 that will be 1024.
In how many ways can 4 red, 3 yellow and 2 green chairs be arranged in a row if the chairs of the same colour are indistinguishable?- a)15120
- b)1260
- c)362880
- d)None of the above
Correct answer is option 'B'. Can you explain this answer?
In how many ways can 4 red, 3 yellow and 2 green chairs be arranged in a row if the chairs of the same colour are indistinguishable?
a)
15120
b)
1260
c)
362880
d)
None of the above
|
|
Hansa Sharma answered |
Total no of balls = 9
red balls = 4
yellow balls = 3
green balls = 2
Total no. of arrangements = 9!/(4!*3!*2!)
= 1260
red balls = 4
yellow balls = 3
green balls = 2
Total no. of arrangements = 9!/(4!*3!*2!)
= 1260
Among 7 flags 4 are of red colour and the rest are all different colours.How mant different signals can be generated using these flags?- a)240
- b)210
- c)180
- d)120
Correct answer is option 'B'. Can you explain this answer?
Among 7 flags 4 are of red colour and the rest are all different colours.How mant different signals can be generated using these flags?
a)
240
b)
210
c)
180
d)
120
|
|
Poonam Reddy answered |
Total flags = 4
Different colour = 3
red = 4
Total no. of signals = 7P3
= 7!/(4!)
= 210
Different colour = 3
red = 4
Total no. of signals = 7P3
= 7!/(4!)
= 210
How many 4 digit numbers are there, when a digit may be repeated any number of times?- a)3×43
- b)9×103
- c)104
- d)410
Correct answer is option 'B'. Can you explain this answer?
How many 4 digit numbers are there, when a digit may be repeated any number of times?
a)
3×43
b)
9×103
c)
104
d)
410
|
|
Nandini Patel answered |
If we assume the leading digit can not be zero, then the first 4-digit number is 1000.
The last 4-digit number is 9999.
—
The number of 4-digit numbers is therefore:
9999 - 1000 + 1 = 9000
——
Another way to calculate this:
1..9 are available for the first digit —> 9 choices
0..9 are available for the 2nd, 3rd, and 4th digits —> 10 choices for each: 10*10*10 = 1000 choices total
and 9*1000 = 9000
A coin is tossed 6 times, in how many throws can 4 heads and 2 tails be obtained?- a)24
- b)18
- c)15
- d)10
Correct answer is option 'C'. Can you explain this answer?
A coin is tossed 6 times, in how many throws can 4 heads and 2 tails be obtained?
a)
24
b)
18
c)
15
d)
10
|
|
Naina Bansal answered |
Whether we toss a coin 6 times or six coins one time the number of arrangement will remain same .
As to find number of ways we get 4 heads and 2 tails out of 6 times
In how many ways, a party of 5 men and 5 women be seated at a circular table, so that no two women are adjacent?- a)720
- b)14400
- c)2880
- d)1440
Correct answer is option 'C'. Can you explain this answer?
In how many ways, a party of 5 men and 5 women be seated at a circular table, so that no two women are adjacent?
a)
720
b)
14400
c)
2880
d)
1440
|
Ayush Joshi answered |
Lets first place the men (M). '*' here indicates the linker of round table
* M -M - M - M - M *
which is in (5-1)! ways
So we have to place the women in between the men which is on the 5 empty seats ( 4 -'s and 1 linker i.e * )
SO 5 women can sit on 5 seats in (5)! ways or
1st seat in 5 ways
2nd seat 4
3rd seat 3
4th seat 2
5th seat 1
i.e 5*4*3*2*1 ways
So the answer is 5! * 4! = 2880
Sonia has 10 balloons out of which 5 are red, 2 white, 2 blue and 1pink, which she wants to use for the decoration. Her favourite pink colour balloon should be filled with toffees and should be put at the centre of the room above the cake table and remaining 9 at the wall behind the cake table. How many ways she can arrange the balloons?- a)956
- b)756
- c)9!
- d)7560
Correct answer is option 'B'. Can you explain this answer?
Sonia has 10 balloons out of which 5 are red, 2 white, 2 blue and 1pink, which she wants to use for the decoration. Her favourite pink colour balloon should be filled with toffees and should be put at the centre of the room above the cake table and remaining 9 at the wall behind the cake table. How many ways she can arrange the balloons?
a)
956
b)
756
c)
9!
d)
7560
|
|
Pooja Shah answered |
1 balloon is fixed that is to be placed above the cake
Now she have to arrange 9 balloons = 9!/(5!*2!*2!)
(9*8*7*6*5!)/((5!*2*2)
= (9*8*7*6)/(2*2)
= 756
Now she have to arrange 9 balloons = 9!/(5!*2!*2!)
(9*8*7*6*5!)/((5!*2*2)
= (9*8*7*6)/(2*2)
= 756
The number of ways in which three different rings can be worn in four fingers with at most one in each finger, are- a)12
- b)64
- c)24
- d)6
Correct answer is 'C'. Can you explain this answer?
The number of ways in which three different rings can be worn in four fingers with at most one in each finger, are
a)
12
b)
64
c)
24
d)
6
|
Gaurav Kumar answered |
The total number of ways is same as the number of arrangements of 4 fingers, taken 3 at a time.
So, required number of ways = 4P3
= 4!/(4-3)!
= 4!/1!
= 4! => 24
So, required number of ways = 4P3
= 4!/(4-3)!
= 4!/1!
= 4! => 24
In a college there are 20 professors including the principal and the vice principal. A committee of 5 is to be formed. In how many ways it can be formed so that neither the principal nor the vice principal is included?- a)C(18,2)
- b)C(20,2)
- c)C(20,18)
- d)C(18,5)
Correct answer is option 'D'. Can you explain this answer?
In a college there are 20 professors including the principal and the vice principal. A committee of 5 is to be formed. In how many ways it can be formed so that neither the principal nor the vice principal is included?
a)
C(18,2)
b)
C(20,2)
c)
C(20,18)
d)
C(18,5)
|
|
Preeti Iyer answered |
Out of 20 professors, excluding the principal and vice-principal, 18 professors are left.
No. of ways of selecting 5 professors out of 18 = 18C5
No. of ways of selecting 5 professors out of 18 = 18C5
The expansion of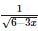 
, in powers of x, is valid if- a)|x| > 2
- b)x < 2
- c)x > 2
- d)|x| < 2
Correct answer is option 'D'. Can you explain this answer?
The expansion of 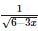, in powers of x, is valid if
, in powers of x, is valid ifa)
|x| > 2
b)
x < 2
c)
x > 2
d)
|x| < 2
|
Knowledge Hub answered |
In case of negative or fractional power, expansion (1+x)^n is valid only when |x| < 1
(6 - 3x)-1/2
= (6-1/2 (1 - x/2)-1/2)
So, this equation exists only when |x/2| < 1
|x| < 2
(6 - 3x)-1/2
= (6-1/2 (1 - x/2)-1/2)
So, this equation exists only when |x/2| < 1
|x| < 2
In a class, there are 30 boys and 18 girls. The teacher wants to select one boy and one girl to represent the class for quiz competition. In how many ways can the teacher make this selection?- a)625
- b)125
- c)25
- d)540
Correct answer is option 'D'. Can you explain this answer?
In a class, there are 30 boys and 18 girls. The teacher wants to select one boy and one girl to represent the class for quiz competition. In how many ways can the teacher make this selection?
a)
625
b)
125
c)
25
d)
540
|
Vijay Kumar answered |
Out of 30 Boys,
No. of ways to select 1 boy = 30C1 = 30
Out of 18 Girls,
No. of ways to select 1 boy = 18C1 = 18
No. of ways of selecting 1 boy and 1 girl =
30*18 = 540
No. of ways to select 1 boy = 30C1 = 30
Out of 18 Girls,
No. of ways to select 1 boy = 18C1 = 18
No. of ways of selecting 1 boy and 1 girl =
30*18 = 540
If n is a +ve integer, then the binomial coefficients equidistant from the beginning and the end in the expansion of (x+a)n are- a)additive inverse of each other
- b)multiplicative inverse of each other
- c)equal
- d)nothing can be said
Correct answer is option 'C'. Can you explain this answer?
If n is a +ve integer, then the binomial coefficients equidistant from the beginning and the end in the expansion of (x+a)n are
a)
additive inverse of each other
b)
multiplicative inverse of each other
c)
equal
d)
nothing can be said
|
|
Hansa Sharma answered |
(x+a)n = nC0 xn + nC1 x(n-1) a1 + nC2 x(n-2) a2 + ..........+ nC(n-1) xa(n-1) + nCn an
Now, nC0 = nCn, nC1 = nCn-1, nC2 = nCn-2,........
therefore, nCr = nCn-r
The binomial coefficients equidistant from the beginning and the end in the expansion of (x+a)n are equal.
Now, nC0 = nCn, nC1 = nCn-1, nC2 = nCn-2,........
therefore, nCr = nCn-r
The binomial coefficients equidistant from the beginning and the end in the expansion of (x+a)n are equal.
A coin is tossed n times, the number of all the possible outcomes is- a)C(n , 2)
- b)P(n , 2)
- c)2n
- d)2n
Correct answer is option 'D'. Can you explain this answer?
A coin is tossed n times, the number of all the possible outcomes is
a)
C(n , 2)
b)
P(n , 2)
c)
2n
d)
2n
|
Krishna Iyer answered |
If coin is tossed n times then possible number of outcomes = 2n
8Cr = 8Cp. So- a)r = p or r = 8p
- b)r = p or r + p = 8
- c)r = p or r – p = 8
- d)r = p or r = 2p
Correct answer is option 'B'. Can you explain this answer?
8Cr = 8Cp. So
a)
r = p or r = 8p
b)
r = p or r + p = 8
c)
r = p or r – p = 8
d)
r = p or r = 2p
|
|
Aryan Khanna answered |
8Cr = 8Cp = 8C8-p
So, either r = p or r = 8 – p
i.e. r = p or r + p = 8
So, either r = p or r = 8 – p
i.e. r = p or r + p = 8
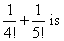
- a)4/5!
- b)5/5!
- c)6/5!
- d)1/5!
Correct answer is option 'C'. Can you explain this answer?
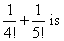
a)
4/5!
b)
5/5!
c)
6/5!
d)
1/5!
|
|
Pooja Shah answered |
1/4! + 1/5!
= 1/4![1 + 1/5]
1/4![6/5]
=> 6/5!
= 1/4![1 + 1/5]
1/4![6/5]
=> 6/5!
The number of different ways in which a man can invite one or more of his 6 friends to dinner is- a)63
- b)15
- c)30
- d)120
Correct answer is option 'A'. Can you explain this answer?
The number of different ways in which a man can invite one or more of his 6 friends to dinner is
a)
63
b)
15
c)
30
d)
120
|
|
Om Desai answered |
He can invite one or more friends by inviting 1 friend, or 2 friends or 3 friends, or all the 6 friends.
1 friend can be selected out of 6 in 6C1 = 6 ways
2 friends can be selected out of 6 in 6C2 = 15 ways
3 friends can be selected out of 6 in 6C3 = 20 ways
4 friends can be selected out of 6 in 6C4 = 15 ways
5 friends can be selected out of 6 in 6C5 = 6 ways
6 friends can be selected out of 6 in 6C6 = 1 ways
Therefore the required number of ways (combinations) = 6 + 15 + 20 + 15 + 6 + 1 = 63
1 friend can be selected out of 6 in 6C1 = 6 ways
2 friends can be selected out of 6 in 6C2 = 15 ways
3 friends can be selected out of 6 in 6C3 = 20 ways
4 friends can be selected out of 6 in 6C4 = 15 ways
5 friends can be selected out of 6 in 6C5 = 6 ways
6 friends can be selected out of 6 in 6C6 = 1 ways
Therefore the required number of ways (combinations) = 6 + 15 + 20 + 15 + 6 + 1 = 63
If nC8 = nC2, then n is- a)8
- b)12
- c)10
- d)2
Correct answer is option 'C'. Can you explain this answer?
If nC8 = nC2, then n is
a)
8
b)
12
c)
10
d)
2
|
Srestha Choudhary answered |
Explanation:
To solve this problem, we need to use the formula for the combination (nCr), which is given by:
nCr = n! / (r!(n-r)!)
where n is the total number of objects, and r is the number of objects chosen at a time.
Given that nC8 = nC2, we can set up the equation as follows:
n! / (8!(n-8)!) = n! / (2!(n-2)!)
To simplify the equation, we can cancel out the common terms on both sides:
(n-2)! * 8! = (n-8)! * 2!
Now, let's expand the factorials:
(n-2)! * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = (n-8)! * 2 * 1
Cancel out the common terms:
8 * 7 * 6 * 5 * 4 * 3 = (n-8)!
We are left with:
8 * 7 * 6 * 5 * 4 * 3 = (n-8)!
Now, let's evaluate the factorial on the left side:
8 * 7 * 6 * 5 * 4 * 3 = 20160
So, we have:
20160 = (n-8)!
To find the value of n, we need to determine the value of (n-8)!. We can do this by finding the factorial of numbers from 1 to 8 until we find a number that is equal to or greater than 20160.
By evaluating the factorials, we find that 8! = 40320, which is greater than 20160. The next factorial, 7!, is equal to 5040, which is less than 20160.
Therefore, n must be greater than 8 but less than 16. The only option that satisfies this condition is option 'C', which is 10.
Hence, the correct answer is option 'C'.
To solve this problem, we need to use the formula for the combination (nCr), which is given by:
nCr = n! / (r!(n-r)!)
where n is the total number of objects, and r is the number of objects chosen at a time.
Given that nC8 = nC2, we can set up the equation as follows:
n! / (8!(n-8)!) = n! / (2!(n-2)!)
To simplify the equation, we can cancel out the common terms on both sides:
(n-2)! * 8! = (n-8)! * 2!
Now, let's expand the factorials:
(n-2)! * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = (n-8)! * 2 * 1
Cancel out the common terms:
8 * 7 * 6 * 5 * 4 * 3 = (n-8)!
We are left with:
8 * 7 * 6 * 5 * 4 * 3 = (n-8)!
Now, let's evaluate the factorial on the left side:
8 * 7 * 6 * 5 * 4 * 3 = 20160
So, we have:
20160 = (n-8)!
To find the value of n, we need to determine the value of (n-8)!. We can do this by finding the factorial of numbers from 1 to 8 until we find a number that is equal to or greater than 20160.
By evaluating the factorials, we find that 8! = 40320, which is greater than 20160. The next factorial, 7!, is equal to 5040, which is less than 20160.
Therefore, n must be greater than 8 but less than 16. The only option that satisfies this condition is option 'C', which is 10.
Hence, the correct answer is option 'C'.
The number of all numbers that can be formed by using some or all of the digits 1, 3, 5, 7, 9 (without repetitions) is- a)325
- b)120
- c)32
- d)none of these
Correct answer is option 'A'. Can you explain this answer?
The number of all numbers that can be formed by using some or all of the digits 1, 3, 5, 7, 9 (without repetitions) is
a)
325
b)
120
c)
32
d)
none of these
|
|
Pooja Shah answered |
Out of 1, 3, 5, 7, 9
No. of 1-digit numbers = 5
No. of 2-digit numbers = 5*4 = 20
No. of 3-digit numbers = 5*4*3 = 60
No. of 4-digit numbers = 5*4*3*2 = 120
No. of 5-digit numbers = 5*4*3*2*1 = 120
Total no. of numbers = 5 + 20 + 60 + 120 + 120 = 325
No. of 1-digit numbers = 5
No. of 2-digit numbers = 5*4 = 20
No. of 3-digit numbers = 5*4*3 = 60
No. of 4-digit numbers = 5*4*3*2 = 120
No. of 5-digit numbers = 5*4*3*2*1 = 120
Total no. of numbers = 5 + 20 + 60 + 120 + 120 = 325
The coefficient of y in the expansion of (y² + c/y)5 is - a)10c
- b)10c²
- c)10c³
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
The coefficient of y in the expansion of (y² + c/y)5 is
a)
10c
b)
10c²
c)
10c³
d)
None of these
|
|
Varun Kapoor answered |
Given, binomial expression is (y² + c / y)5
Now, Tr+1 = 5Cr × (y²)5-r × (c / y)r
= 5Cr × y10-3r × Cr
Now, 10 – 3r = 1
⇒ 3r = 9
⇒ r = 3
So, the coefficient of y = 5C3 × c³ = 10c³
Now, Tr+1 = 5Cr × (y²)5-r × (c / y)r
= 5Cr × y10-3r × Cr
Now, 10 – 3r = 1
⇒ 3r = 9
⇒ r = 3
So, the coefficient of y = 5C3 × c³ = 10c³
A committee of 7 has to be formed from 9 boys and 4 girls.In how many ways can this be done when the committee consists of Exactly 3 girls?
|
|
Shiksha Academy answered |
out of 7 persons , we have to select exactly 3 girls . hence, it's clear that remaining 4 persons will be boys .
Now, number of ways taken 4 boys from 9 boys = 9C4
and number of ways taken 3 girls from 4 girls = 4C3
hence, by fundamental principle of counting ,
total number of ways for making the committee = 9C4 × 4C3
= 9!/5!.4! × 4!/3!
= 9×8×7×6/3×2×1
= 9×8×7
= 504 ways
Now, number of ways taken 4 boys from 9 boys = 9C4
and number of ways taken 3 girls from 4 girls = 4C3
hence, by fundamental principle of counting ,
total number of ways for making the committee = 9C4 × 4C3
= 9!/5!.4! × 4!/3!
= 9×8×7×6/3×2×1
= 9×8×7
= 504 ways
If (n + 1)! = 20(n – 1)!, then n is equal to- a)20
- b)5
- c)-5
- d)4
Correct answer is option 'D'. Can you explain this answer?
If (n + 1)! = 20(n – 1)!, then n is equal to
a)
20
b)
5
c)
-5
d)
4
|
|
Vikas Kapoor answered |
(n + 1)! = 20 (n – 1)!
n (n + 1) = 20
(n – 4) (n + 5) = 0
Since, (n – 1)! exists, n ≥ 1
So, n = 4
n (n + 1) = 20
(n – 4) (n + 5) = 0
Since, (n – 1)! exists, n ≥ 1
So, n = 4
The number of three digit numbers having atleast one digit as 5 is- a)225
- b)246
- c)648
- d)252
Correct answer is option 'D'. Can you explain this answer?
The number of three digit numbers having atleast one digit as 5 is
a)
225
b)
246
c)
648
d)
252
|
|
Ravi Sharma answered |
These digit number without digit 5 →100....999
→ these are 900 three-digit number
→ from 100 to 199 → 19 number with 5.
200−299→19
300−399→19
400−499→19
600−699→19
700−799→19
800−899→19
900−999→19
500−599→100
total number with 5=19×8+100 for (500-599)
=152+100
=252
→ these are 900 three-digit number
→ from 100 to 199 → 19 number with 5.
200−299→19
300−399→19
400−499→19
600−699→19
700−799→19
800−899→19
900−999→19
500−599→100
total number with 5=19×8+100 for (500-599)
=152+100
=252
On a railway track, there are 20 stations. The number of tickets required in order that it may be possible to book a passenger from every station to every other is- a)C(20,2)
- b)P(20,2)
- c)400
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
On a railway track, there are 20 stations. The number of tickets required in order that it may be possible to book a passenger from every station to every other is
a)
C(20,2)
b)
P(20,2)
c)
400
d)
none of these
|
|
Chirag Verma answered |
Number of tickets selected from first station =20
from second =19
.... for last station =0
We have to select 2 consecutive stations
so total number of possible tickets = P(20,2)
from second =19
.... for last station =0
We have to select 2 consecutive stations
so total number of possible tickets = P(20,2)
The figures 4, 5, 6, 7, 8 are written in every possible order. The number of numbers greater than 56000 is- a)98
- b)72
- c)90
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
The figures 4, 5, 6, 7, 8 are written in every possible order. The number of numbers greater than 56000 is
a)
98
b)
72
c)
90
d)
none of these
|
|
Riya Banerjee answered |
There are in total 6 numbers, 4,5,6,7,8.
Now consider the number 56000
Consider the numbers of the form
56−−−.
Considering no repetitions we get
3×2×1 = 6 numbers.
Similarly for 57−−− and 58−−−.
Hence 3×6 = 18 numbers.
Now consider the numbers starting with 6.
6−−−−
We get 4×3×2×1 = 24.
Similarly for the numbers starting with 7 and 8 we get in total 24 numbers each.
Hence total number of numbers greater than 56000 will be
= (24×3)+18
= 72+18 = 90
Now consider the number 56000
Consider the numbers of the form
56−−−.
Considering no repetitions we get
3×2×1 = 6 numbers.
Similarly for 57−−− and 58−−−.
Hence 3×6 = 18 numbers.
Now consider the numbers starting with 6.
6−−−−
We get 4×3×2×1 = 24.
Similarly for the numbers starting with 7 and 8 we get in total 24 numbers each.
Hence total number of numbers greater than 56000 will be
= (24×3)+18
= 72+18 = 90
Find the number of diagonals of an n-sided polygon.- a)n
- b)(n-1)
- c)n(n-1)/2
- d)n(n-3)/2
Correct answer is option 'D'. Can you explain this answer?
Find the number of diagonals of an n-sided polygon.
a)
n
b)
(n-1)
c)
n(n-1)/2
d)
n(n-3)/2
|
|
Charvi Chakraborty answered |
Solution:
To find the number of diagonals of an n-sided polygon, we need to understand what a diagonal is and how many diagonals are present in a polygon.
What is a diagonal?
A diagonal is a line segment that connects two non-adjacent vertices of a polygon.
How many diagonals are present in a polygon?
To count the number of diagonals in a polygon, we need to consider each vertex of the polygon and count the number of diagonals that can be drawn from that vertex.
For example, consider a square.
https://www.edurev.in/ckeditor_assets/pictures/8521/content_diagonal1.png" />
There are four vertices in the square. If we start with the top-left vertex and count the number of diagonals that can be drawn from that vertex, we get two diagonals. Similarly, if we count from the top-right vertex, we get two diagonals. If we count from the bottom-left vertex, we get two diagonals, and if we count from the bottom-right vertex, we get two diagonals. So, in total, there are eight diagonals in a square.
This method works for any polygon. For an n-sided polygon, we have n vertices, and if we count the number of diagonals that can be drawn from each vertex, we get:
- From each vertex, we can draw n-3 diagonals (because we cannot draw a diagonal to the adjacent vertices or to itself).
- Since there are n vertices, the total number of diagonals in an n-sided polygon is:
n(n-3)/2
Therefore, the correct option is (D) n(n-3)/2.
To find the number of diagonals of an n-sided polygon, we need to understand what a diagonal is and how many diagonals are present in a polygon.
What is a diagonal?
A diagonal is a line segment that connects two non-adjacent vertices of a polygon.
How many diagonals are present in a polygon?
To count the number of diagonals in a polygon, we need to consider each vertex of the polygon and count the number of diagonals that can be drawn from that vertex.
For example, consider a square.
There are four vertices in the square. If we start with the top-left vertex and count the number of diagonals that can be drawn from that vertex, we get two diagonals. Similarly, if we count from the top-right vertex, we get two diagonals. If we count from the bottom-left vertex, we get two diagonals, and if we count from the bottom-right vertex, we get two diagonals. So, in total, there are eight diagonals in a square.
This method works for any polygon. For an n-sided polygon, we have n vertices, and if we count the number of diagonals that can be drawn from each vertex, we get:
- From each vertex, we can draw n-3 diagonals (because we cannot draw a diagonal to the adjacent vertices or to itself).
- Since there are n vertices, the total number of diagonals in an n-sided polygon is:
n(n-3)/2
Therefore, the correct option is (D) n(n-3)/2.
Find the number of words with or without meaning which can be made using all the letters of the word SWEET.- a)120
- b)24
- c)48
- d)60
Correct answer is option 'D'. Can you explain this answer?
Find the number of words with or without meaning which can be made using all the letters of the word SWEET.
a)
120
b)
24
c)
48
d)
60
|
Md Jisan answered |
Sweet has 5 letters, so it gives 5! but there are two letters which are same , so number of words will be = (5! ÷ 2!) = 60
How many three letter codes can be formed by only vowels of English alphabets, given that repetition of letters is allowed?- a)125
- b)5
- c)25
- d)5!
Correct answer is option 'A'. Can you explain this answer?
How many three letter codes can be formed by only vowels of English alphabets, given that repetition of letters is allowed?
a)
125
b)
5
c)
25
d)
5!
|
Ishan Choudhury answered |
We have 5 choices (a, e, i, o, u)
3 letter codes = 5 * 5 * 5
= 125
3 letter codes = 5 * 5 * 5
= 125
C(20,r) = C(20, r + 2) What is the value of C(r,6) ?- a)84
- b)24
- c)48
- d)12
Correct answer is option 'A'. Can you explain this answer?
C(20,r) = C(20, r + 2) What is the value of C(r,6) ?
a)
84
b)
24
c)
48
d)
12
|
|
Suresh Reddy answered |
20Cr = 20Cr+2
nCr = nCn-r
=> r + (n−r) = n
⇒ r + r + 2 = 20
⇒ 2r = 18
⇒ r = 9
rC6 = 9C6
⇒ 9!/(6!*3!)
= 84
nCr = nCn-r
=> r + (n−r) = n
⇒ r + r + 2 = 20
⇒ 2r = 18
⇒ r = 9
rC6 = 9C6
⇒ 9!/(6!*3!)
= 84
A team of 7 players is to be formed out of 5 under 19 players and 6 senior players. In how many ways, the team can be chosen when at least 4 senior players are included?- a)185
- b)215
- c)115
- d)125
Correct answer is option 'B'. Can you explain this answer?
A team of 7 players is to be formed out of 5 under 19 players and 6 senior players. In how many ways, the team can be chosen when at least 4 senior players are included?
a)
185
b)
215
c)
115
d)
125
|
|
Om Desai answered |
No. of ways to select 4 senior and 3 U-19 players = 6C4 * 5C3 = 150
No. of ways to select 5 senior and 2 U-19 players = 6C5 * 5C2 = 60
No. of ways to select 6 senior and 1 U-19 players = 6C6 * 5C1 = 5
Total no. of ways to select the team = 150 + 60 + 5 = 215
No. of ways to select 5 senior and 2 U-19 players = 6C5 * 5C2 = 60
No. of ways to select 6 senior and 1 U-19 players = 6C6 * 5C1 = 5
Total no. of ways to select the team = 150 + 60 + 5 = 215
Chapter doubts & questions for Binomial Theorem - Online MCQ Tests for Commerce 2025 is part of Commerce exam preparation. The chapters have been prepared according to the Commerce exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Commerce 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Binomial Theorem - Online MCQ Tests for Commerce in English & Hindi are available as part of Commerce exam.
Download more important topics, notes, lectures and mock test series for Commerce Exam by signing up for free.
|
© EduRev
|
Education Revolution
|
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily