All Exams >
CUET Commerce >
General Test Preparation for CUET UG >
All Questions
All questions of Distance & Direction for CUET Commerce Exam
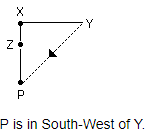
Salim started walking from point 'P' towards South. After walking 40 metres, he took a left turn and walked 30 metres and reached point Q. What is the straight line distance between P and Q, and Q is towards which direction of P?
- a)35 meters South-East
- b)50 meters South-West
- c)35 meters South-West
- d)50 meters South-East
Correct answer is option 'D'. Can you explain this answer?
Salim started walking from point 'P' towards South. After walking 40 metres, he took a left turn and walked 30 metres and reached point Q. What is the straight line distance between P and Q, and Q is towards which direction of P?
a)
35 meters South-East
b)
50 meters South-West
c)
35 meters South-West
d)
50 meters South-East

|
Arya Roy answered |
As per the given information;
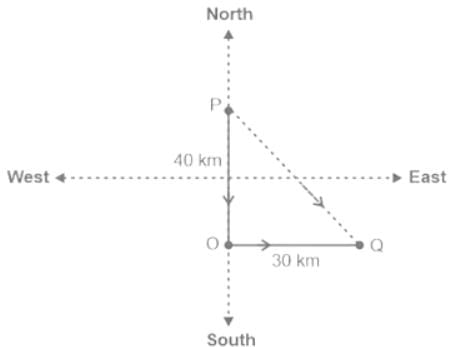

Point Q is in South East of Point P.
Distance between P and Q (PQ) = √(PO2 + OQ2)
PQ = √(402 + 302)
PQ = √(1600 + 900)
PQ = √2500
PQ = 50 m
Hence, "50 metres, Southeast" is the correct answer.
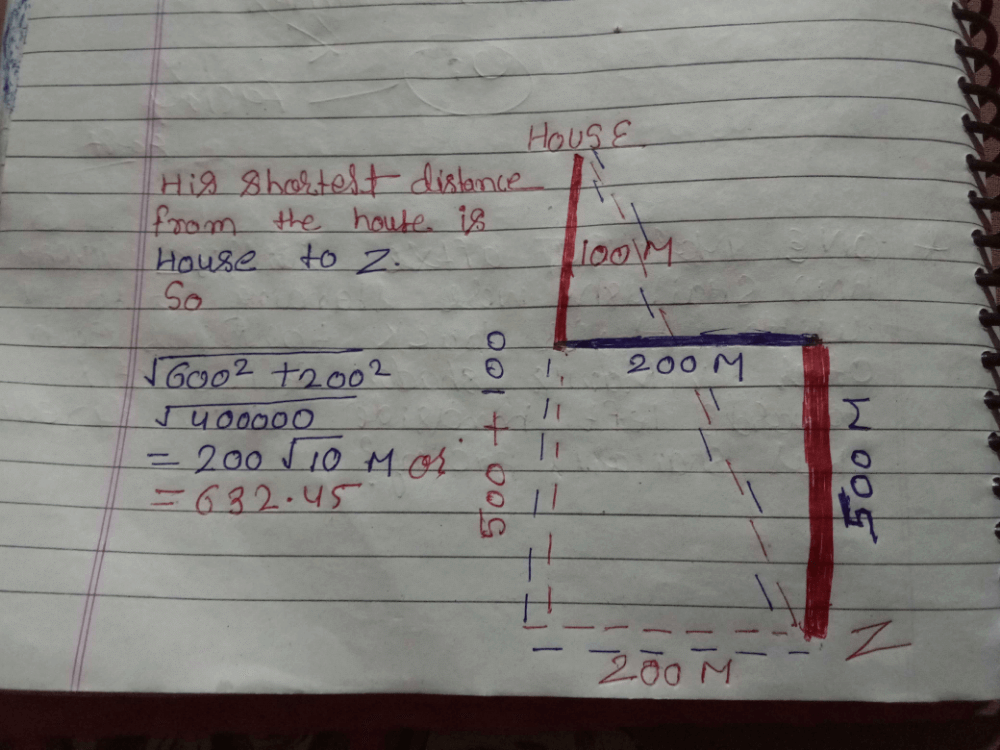
Sonu started from his house and walked 3 km Eastward, then he turned right and walked 2 km, then again he turned left and walked 1 km. Again he turned left and walked 3 km, then turned right and walked 2 km. He turned right again and walked 1 km and reached his school. What is the shortest distance between Sonu's house and his school?
- a)12 km
- b)9km
- c)5 km
- d)6 km
Correct answer is option 'D'. Can you explain this answer?
Sonu started from his house and walked 3 km Eastward, then he turned right and walked 2 km, then again he turned left and walked 1 km. Again he turned left and walked 3 km, then turned right and walked 2 km. He turned right again and walked 1 km and reached his school. What is the shortest distance between Sonu's house and his school?
a)
12 km
b)
9km
c)
5 km
d)
6 km

|
Vertex Academy answered |
To solve this, let's break down Hemant's movements step by step and visualize his path:
- Hemant starts from his house and walks 3 km eastward.
- He turns right and walks 2 km south.
- He turns left and walks 1 km east.
- He turns right and walks 2 km south.
- He turns right and walks 1 km west and reaches his school.
Now, let's consider the overall east-west and north-south movement:
- East-West: Hemant initially walked 3 km east, then 1 km east, and finally 1 km west. So, the net eastward distance is 3 + 1 − 1 = 3 km.
- North-South: Hemant walked 2 km south, then another 2 km south, so he walked a total of 2 + 2 = 4 km south.
The minimum distance from Hemant’s house to the school can be found using the Pythagorean theorem (since he moved in perpendicular directions):
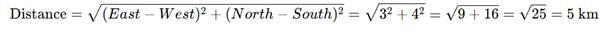
Thus, the minimum distance between Hemant’s house and his school is: D: 5 km
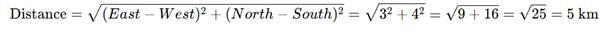
Thus, the minimum distance between Hemant’s house and his school is: D: 5 km
A starts from his house and moves towards B’s house which is 4km North. After walking for three-fourth of the distance he finds B coming towards him along with C, who is A’s enemy. Wanting to avoid him, A takes a left turn and runs for a distance of 2kms.Now, if from this point (say ‘P’) he decides to go to B’s house
How far is A, from his own house?
A. √5km
B. √3km
C. √7km
D. √13km
Correct answer is option is 'D'. Can you explain this answer?

|
Vertex Academy answered |
1. A walks three-fourths of the distance towards B's house, which is:
(3/4) × 4 km = 3 km (north).
After walking 3 km north, A takes a left turn and runs 2 km west.
(3/4) × 4 km = 3 km (north).
After walking 3 km north, A takes a left turn and runs 2 km west.
2. Now, we have a right-angled triangle, where:
- One leg (north) = 3 km,
- Another leg (west) = 2 km.
- One leg (north) = 3 km,
- Another leg (west) = 2 km.
3. The distance from A’s current position (P) to his house is the hypotenuse of this right-angled triangle:
Distance = √(3² + 2²) = √(9 + 4) = √13 km.
Distance = √(3² + 2²) = √(9 + 4) = √13 km.
Thus, the distance from A’s current position to his own house is √13 km.
If a man on the moped starts from a point and rides 4km south, then turns left and rides 2km, then turn again to the right to ride 4km more, towards which direction is he moving?- a)North
- b)West
- c)East
- d)South
Correct answer is 'D'. Can you explain this answer?
If a man on the moped starts from a point and rides 4km south, then turns left and rides 2km, then turn again to the right to ride 4km more, towards which direction is he moving?
a)
North
b)
West
c)
East
d)
South

|
Raghavendra Sharma answered |
Man's walking directions are as follows:
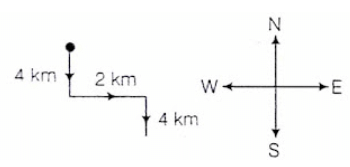

If A is to the south of B, and C is to the east of B, in what direction is A with respect to C?- a)North-East
- b)North-West
- c)South-East
- d)South-West
Correct answer is option 'D'. Can you explain this answer?
If A is to the south of B, and C is to the east of B, in what direction is A with respect to C?
a)
North-East
b)
North-West
c)
South-East
d)
South-West

|
Sameer Rane answered |
Clearly comparing the direction of A w.r.t C in the second diagram with that in the first diagram, A will be south-west of C
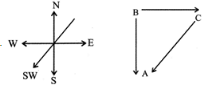
Lakshay starting walking towards west and goes 10km. Then he turns left and goes 8km. He again turns left and goes 18km. In which direction is he now from his starting point? - a)South-West
- b)North-East
- c)South-East
- d)North-West
Correct answer is option 'C'. Can you explain this answer?
Lakshay starting walking towards west and goes 10km. Then he turns left and goes 8km. He again turns left and goes 18km. In which direction is he now from his starting point?
a)
South-West
b)
North-East
c)
South-East
d)
North-West

|
Vertex Academy answered |
From the figure given, clearly the direction is OC which is South-East.
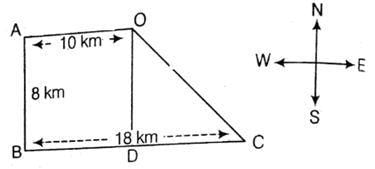

Sushant started from his house and walked 5km north of his house. Then he turned left and walked 3km, then he turned right and walked 5km. Again he turned right and walked 3km. Where is his final destination from his house?- a)Back to his house
- b)7.5 km North-West
- c)7.5 km North-East
- d)10 km North
Correct answer is option 'D'. Can you explain this answer?
Sushant started from his house and walked 5km north of his house. Then he turned left and walked 3km, then he turned right and walked 5km. Again he turned right and walked 3km. Where is his final destination from his house?
a)
Back to his house
b)
7.5 km North-West
c)
7.5 km North-East
d)
10 km North

|
Vertex Academy answered |
To solve this question, let's analyze Sushant's path step-by-step based on the directions provided:
- Sushant starts at his house and walks 5 km north.
- He then turns left and walks 3 km west.
- Next, he turns right and walks 5 km north again.
- Finally, he turns right and walks 3 km east.
Now let’s assess Sushant's final position relative to his starting point:
- North-South movement: He walked 5 km north, then another 5 km north, totaling 10 km north.
- East-West movement: He walked 3 km west and then 3 km back east, which brings him back to the original east-west position he started from.
Given this analysis, Sushant's final destination is directly north of his house without any deviation east or west. Therefore, the correct answer is:
D: 10 km North
Mohan was facing east. he walked 4 km forward and then after turning to his right walked 3 km. Again he turned to his right and walked 4 km. After this he turned back. Which direction, was he facing at that time?
- a)East
- b)West
- c)North
- d)South
Correct answer is option 'A'. Can you explain this answer?
Mohan was facing east. he walked 4 km forward and then after turning to his right walked 3 km. Again he turned to his right and walked 4 km. After this he turned back. Which direction, was he facing at that time?
a)
East
b)
West
c)
North
d)
South
|
|
Kiran Reddy answered |
According to given data let's make Mohan walking route direction;
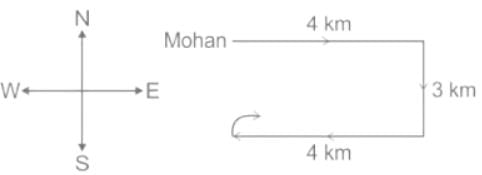

Before turning back his face was in West direction.
After turned back his face should be in 'East' direction.
Hence, the correct answer is "East".
A direction pole was situated on the crossing. Due to an accident the pole turned in such a manner that the pointer which was showing East, started showing South. One traveler went to the wrong direction thinking it to be West. In what direction actually he was travelling?a)South-Westb)Eastc)Southd)NorthCorrect answer is option 'D'. Can you explain this answer?

|
Bijoy Pillai answered |
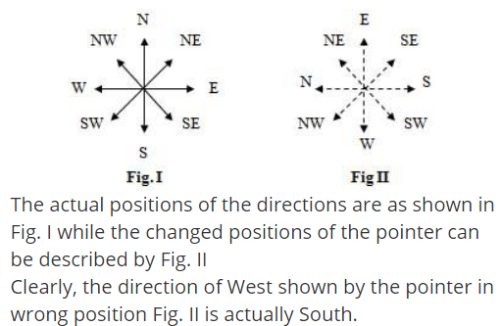
CORRECT OPTION IS (D).
You can clear all the concepts of LR- DI and can solve more questions for CAT through the course provided below:
From her house, Avantika went 15 km to the North, then, she turned West and covered 10 km. Then, she turned South and covered 5 km. Finally, turning to East, she covered 10 km. In which direction is she from her house?
- a)East
- b)West
- c)North
- d)South
Correct answer is option 'C'. Can you explain this answer?
From her house, Avantika went 15 km to the North, then, she turned West and covered 10 km. Then, she turned South and covered 5 km. Finally, turning to East, she covered 10 km. In which direction is she from her house?
a)
East
b)
West
c)
North
d)
South

|
Future Foundation Institute answered |
Therefore, it is clear that he is in the North from his house.
If South East becomes North, North East becomes West and this trend is continued, what will be the original West become?- a)North-East
- b)South-East
- c)South
- d)South-West
Correct answer is option 'B'. Can you explain this answer?
If South East becomes North, North East becomes West and this trend is continued, what will be the original West become?
a)
North-East
b)
South-East
c)
South
d)
South-West

|
Manoj Ghosh answered |
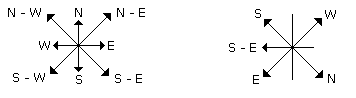
It is clear from the diagrams that new name of West will become South-East.
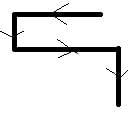
Rohan starts for morning walk towards west. He walks 1 km, then turns left and walks 600m, then turns left and walks 1.3km, again he turns right and walks 600m further. In which direction is he moving now?- a)North
- b)East
- c)West
- d)South
Correct answer is option 'D'. Can you explain this answer?
Rohan starts for morning walk towards west. He walks 1 km, then turns left and walks 600m, then turns left and walks 1.3km, again he turns right and walks 600m further. In which direction is he moving now?
a)
North
b)
East
c)
West
d)
South
|
|
Kiran Reddy answered |
Rohan is walking in south now
Vipul moves towards South-East a distance of 14m, then he moves towards west and travels a distance of 28m. From here, he moves towards North-West a distance of 14m and finally he moves a distance of 8m towards east and comes to a half. How far is he from the starting point where he stood.- a)20m
- b)22m
- c)6m
- d)8m
Correct answer is option 'A'. Can you explain this answer?
Vipul moves towards South-East a distance of 14m, then he moves towards west and travels a distance of 28m. From here, he moves towards North-West a distance of 14m and finally he moves a distance of 8m towards east and comes to a half. How far is he from the starting point where he stood.
a)
20m
b)
22m
c)
6m
d)
8m
|
|
Dia Mehta answered |
A is the correct option.
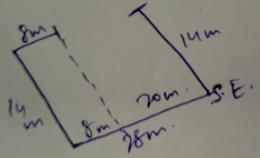

One morning after sunrise, Sunil was standing facing a pole. The shadow of the pole fell exactly to his right, which direction was he facing?- a)East
- b)South
- c)North
- d)Data inadequate
Correct answer is option 'B'. Can you explain this answer?
One morning after sunrise, Sunil was standing facing a pole. The shadow of the pole fell exactly to his right, which direction was he facing?
a)
East
b)
South
c)
North
d)
Data inadequate

|
Vertex Academy answered |
One morning after sunrise, Sunil was standing facing a pole. The shadow of the pole fell exactly to his right.
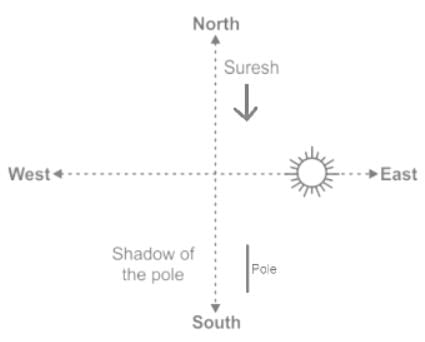

Clearly, Sunil is facing South direction.
Hence, 'South' is the correct answer.
Gaurav walks 20 metres towards North. He then turns left and walks 40 metres. He again turns left and walks 20 metres. Further, he moves 20 metres after turning to the right. How far is he from his original position ?- a)40 metres
- b)50 metres
- c)60 metres
- d)70 metres
Correct answer is option 'C'. Can you explain this answer?
Gaurav walks 20 metres towards North. He then turns left and walks 40 metres. He again turns left and walks 20 metres. Further, he moves 20 metres after turning to the right. How far is he from his original position ?
a)
40 metres
b)
50 metres
c)
60 metres
d)
70 metres
|
|
Kiran Reddy answered |
Final distance from original position = AE = AD + DE = 60 metres
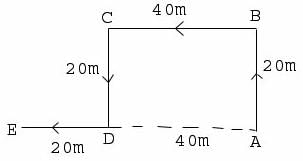
Two buses start from the opposite points of a main road, 150 km apart. The first bus runs for 25 km and takes a right turn and then runs for 15 km. It then turns left and runs for another 25 km and takes the direction back to reach the main road. In the meantime, due to a minor breakdown, the other bus has run only 35 km along the main road. What would be the distance between the two buses at this point ?
- a)65 km
- b)75 km
- c)80 km
- d)85 km
Correct answer is option 'A'. Can you explain this answer?
Two buses start from the opposite points of a main road, 150 km apart. The first bus runs for 25 km and takes a right turn and then runs for 15 km. It then turns left and runs for another 25 km and takes the direction back to reach the main road. In the meantime, due to a minor breakdown, the other bus has run only 35 km along the main road. What would be the distance between the two buses at this point ?
a)
65 km
b)
75 km
c)
80 km
d)
85 km

|
Priyanka Menon answered |
Given information:
- Two buses start from opposite points of a main road, 150 kms apart.
- The first bus runs for 25kms and takes a right turn and then runs for 15 kms.
- It then turns left and runs for another 25 kms and takes the direction back to reach the main road.
- The other bus has run only 35 kms along the main road.
To find:
- The distance between the two buses at this point.
Explanation:
Let's assume that the two buses meet at point X on the main road.
- The first bus travels a total distance of 25 + 15 + 25 = 65 kms before reaching point X.
- The second bus travels a total distance of 35 kms before reaching point X.
- Therefore, the distance between the two buses at point X is 150 - (65 + 35) = 50 kms.
Now, we need to find the distance between the two buses at the point where the first bus reaches the main road again.
- The first bus has covered a total distance of 2 * 25 + 15 = 65 kms from its starting point to reach the main road again.
- The second bus has covered a total distance of 35 + 25 = 60 kms from its starting point to reach the point where the first bus reached the main road again.
- Therefore, the distance between the two buses at this point is 150 - (65 + 60) = 25 kms.
Therefore, the distance between the two buses at the point where the first bus reaches the main road again is 25 kms.
Answer: Option A) 65 kms.
- Two buses start from opposite points of a main road, 150 kms apart.
- The first bus runs for 25kms and takes a right turn and then runs for 15 kms.
- It then turns left and runs for another 25 kms and takes the direction back to reach the main road.
- The other bus has run only 35 kms along the main road.
To find:
- The distance between the two buses at this point.
Explanation:
Let's assume that the two buses meet at point X on the main road.
- The first bus travels a total distance of 25 + 15 + 25 = 65 kms before reaching point X.
- The second bus travels a total distance of 35 kms before reaching point X.
- Therefore, the distance between the two buses at point X is 150 - (65 + 35) = 50 kms.
Now, we need to find the distance between the two buses at the point where the first bus reaches the main road again.
- The first bus has covered a total distance of 2 * 25 + 15 = 65 kms from its starting point to reach the main road again.
- The second bus has covered a total distance of 35 + 25 = 60 kms from its starting point to reach the point where the first bus reached the main road again.
- Therefore, the distance between the two buses at this point is 150 - (65 + 60) = 25 kms.
Therefore, the distance between the two buses at the point where the first bus reaches the main road again is 25 kms.
Answer: Option A) 65 kms.
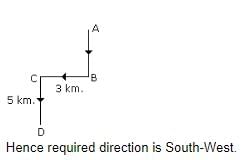
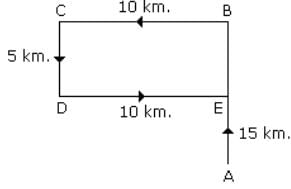
Shehnaz wants to go to the market. She started from her home which is in North and comes to a crossing. The road to her left ends in a park and straight ahead is the office complex. In which direction is the market from crossing?- a)East
- b)West
- c)North
- d)South
Correct answer is option 'B'. Can you explain this answer?
Shehnaz wants to go to the market. She started from her home which is in North and comes to a crossing. The road to her left ends in a park and straight ahead is the office complex. In which direction is the market from crossing?
a)
East
b)
West
c)
North
d)
South

|
Avantika Chakraborty answered |
From the Fig, it is clear that Anoop starts hi... mores journey from point A and finishes his journey at point B. It can be seen that point B is at a distance of 10 m from point A and in the From the Fig, it is clear that Anoop starts his journey from point A and finishes his journey at point B. It can be seen that point B is at a distance of 10 m from point A and in the East direction.
Facing North, Ramesh walks 20 m, then he turns left and walks 30m, then again he turns left and walks 20 m. Then, he turns right and walks 10 m. How far is he now from his starting position?- a)30 m
- b)25 m
- c)40 m
- d)45 m
Correct answer is option 'C'. Can you explain this answer?
Facing North, Ramesh walks 20 m, then he turns left and walks 30m, then again he turns left and walks 20 m. Then, he turns right and walks 10 m. How far is he now from his starting position?
a)
30 m
b)
25 m
c)
40 m
d)
45 m

|
Ishita Choudhury answered |
To solve this problem, we need to visualize Ramesh's movements and calculate the distance between his final position and his starting position.
Let's break down Ramesh's movements step by step:
1. Ramesh walks 20 m facing North.
2. He turns left and walks 30 m.
3. He turns left again and walks 20 m.
4. He turns right and walks 10 m.
Calculating the North-South and East-West distances separately will help us determine the final position.
North-South Distance:
- Ramesh initially walks 20 m facing North.
- Then he turns left and walks 30 m, which means he moves 30 m towards the West.
- Finally, he turns left again and walks 20 m, which means he moves 20 m towards the South.
So, the total North-South distance covered by Ramesh is 20 m (North) - 20 m (South) = 0 m.
East-West Distance:
- Ramesh initially walks 20 m facing North.
- Then he turns left and walks 30 m, which means he moves 30 m towards the West.
- Finally, he turns left again and walks 20 m, which means he moves 20 m towards the South.
- After that, he turns right and walks 10 m, which means he moves 10 m towards the East.
So, the total East-West distance covered by Ramesh is 20 m (West) + 10 m (East) = 30 m.
Using the Pythagorean theorem, we can calculate the distance between Ramesh's final position and his starting position:
Distance = √((North-South Distance)^2 + (East-West Distance)^2)
= √((0 m)^2 + (30 m)^2)
= √(0 + 900)
= √900
= 30 m
Therefore, Ramesh is 30 m away from his starting position. The correct answer is option (a) 30 m.
Let's break down Ramesh's movements step by step:
1. Ramesh walks 20 m facing North.
2. He turns left and walks 30 m.
3. He turns left again and walks 20 m.
4. He turns right and walks 10 m.
Calculating the North-South and East-West distances separately will help us determine the final position.
North-South Distance:
- Ramesh initially walks 20 m facing North.
- Then he turns left and walks 30 m, which means he moves 30 m towards the West.
- Finally, he turns left again and walks 20 m, which means he moves 20 m towards the South.
So, the total North-South distance covered by Ramesh is 20 m (North) - 20 m (South) = 0 m.
East-West Distance:
- Ramesh initially walks 20 m facing North.
- Then he turns left and walks 30 m, which means he moves 30 m towards the West.
- Finally, he turns left again and walks 20 m, which means he moves 20 m towards the South.
- After that, he turns right and walks 10 m, which means he moves 10 m towards the East.
So, the total East-West distance covered by Ramesh is 20 m (West) + 10 m (East) = 30 m.
Using the Pythagorean theorem, we can calculate the distance between Ramesh's final position and his starting position:
Distance = √((North-South Distance)^2 + (East-West Distance)^2)
= √((0 m)^2 + (30 m)^2)
= √(0 + 900)
= √900
= 30 m
Therefore, Ramesh is 30 m away from his starting position. The correct answer is option (a) 30 m.
Study the information and answer the questions given below:
On a playing ground, Dev, Kumar, Nilesh, Ankur and Pintu are starting as directed below facing the North.
i. Kumar is 40 m to the right of Ankur.
ii. Dev is 60 m to the South of Kumar.
iii. NIlesh is 25 m to the West of Ankur.
iv. Pintu is 90 m to the North of Dev.
Who is at the North-East of the person, who is to the left of Kumar?
- a)Nilesh
- b)Ankur
- c)Pintu
- d)Either Nilesh or Dev
Correct answer is option 'C'. Can you explain this answer?
Study the information and answer the questions given below:
On a playing ground, Dev, Kumar, Nilesh, Ankur and Pintu are starting as directed below facing the North.
i. Kumar is 40 m to the right of Ankur.
ii. Dev is 60 m to the South of Kumar.
iii. NIlesh is 25 m to the West of Ankur.
iv. Pintu is 90 m to the North of Dev.
On a playing ground, Dev, Kumar, Nilesh, Ankur and Pintu are starting as directed below facing the North.
i. Kumar is 40 m to the right of Ankur.
ii. Dev is 60 m to the South of Kumar.
iii. NIlesh is 25 m to the West of Ankur.
iv. Pintu is 90 m to the North of Dev.
Who is at the North-East of the person, who is to the left of Kumar?
a)
Nilesh
b)
Ankur
c)
Pintu
d)
Either Nilesh or Dev
|
|
Shreya Ahuja answered |
Answer is c
Jenny walked 2.5 km towards North and turned towards West. After covering 2 km’s he turned to South and walked 1.5 km’s. He then turned to East and covered 2 km’s. How far is Jenny from original point?- a)5 km
- b)2.5 km
- c)1.5 km
- d)1 km
Correct answer is option 'D'. Can you explain this answer?
Jenny walked 2.5 km towards North and turned towards West. After covering 2 km’s he turned to South and walked 1.5 km’s. He then turned to East and covered 2 km’s. How far is Jenny from original point?
a)
5 km
b)
2.5 km
c)
1.5 km
d)
1 km
|
|
Dibyajyoti answered |
Exactly
X and Y started from a fixed point. X moves towards North and after walking 3 km turns to his right and covers 4 km. Y moves towards West and walks 5 km and then turns to his right and walks 3 km. How far X and Y are from each other?- a)5km
- b)9km
- c)6km
- d)10km
Correct answer is option 'B'. Can you explain this answer?
X and Y started from a fixed point. X moves towards North and after walking 3 km turns to his right and covers 4 km. Y moves towards West and walks 5 km and then turns to his right and walks 3 km. How far X and Y are from each other?
a)
5km
b)
9km
c)
6km
d)
10km

|
Sahana Nair answered |
To find out how far X and Y are from each other, we can plot their movements on a coordinate plane.
Let's assume the starting point as the origin (0,0). X moves towards the North, which means it moves along the positive y-axis. After walking 3 km, X turns to its right (clockwise) and covers 4 km. This means X moves 4 km along the positive x-axis. So, the final position of X is (4,3).
Y moves towards the West, which means it moves along the negative x-axis. After walking 5 km, Y turns to its right and covers 3 km. This means Y moves 3 km along the negative y-axis. So, the final position of Y is (-5,-3).
Using the distance formula, we can calculate the distance between the final positions of X and Y:
Distance = √((x2 - x1)^2 + (y2 - y1)^2)
Plugging in the values:
Distance = √((4 - (-5))^2 + (3 - (-3))^2)
= √(9^2 + 6^2)
= √(81 + 36)
= √117
≈ 10.82
Rounding off to the nearest whole number, the distance between X and Y is approximately 11 km.
Therefore, the correct answer is option 'B' - 9 km.
Let's assume the starting point as the origin (0,0). X moves towards the North, which means it moves along the positive y-axis. After walking 3 km, X turns to its right (clockwise) and covers 4 km. This means X moves 4 km along the positive x-axis. So, the final position of X is (4,3).
Y moves towards the West, which means it moves along the negative x-axis. After walking 5 km, Y turns to its right and covers 3 km. This means Y moves 3 km along the negative y-axis. So, the final position of Y is (-5,-3).
Using the distance formula, we can calculate the distance between the final positions of X and Y:
Distance = √((x2 - x1)^2 + (y2 - y1)^2)
Plugging in the values:
Distance = √((4 - (-5))^2 + (3 - (-3))^2)
= √(9^2 + 6^2)
= √(81 + 36)
= √117
≈ 10.82
Rounding off to the nearest whole number, the distance between X and Y is approximately 11 km.
Therefore, the correct answer is option 'B' - 9 km.
Study the information and answer the questions given below:
On a playing ground, Dev, Kumar, Nilesh, Ankur and Pintu are starting as directed below facing the North.
i. Kumar is 40 m to the right of Ankur.
ii. Dev is 60 m to the South of Kumar.
iii. NIlesh is 25 m to the West of Ankur.
iv. Pintu is 90 m to the North of Dev.
If a boy walks from Nilesh, meets Ankur followed by Kumar, Dev and then Pintu, how many metres has he walked, if he has travelled the straight distance all through?
- a)215 m
- b)155 m
- c)245 m
- d)185 m
Correct answer is option 'A'. Can you explain this answer?
Study the information and answer the questions given below:
On a playing ground, Dev, Kumar, Nilesh, Ankur and Pintu are starting as directed below facing the North.
i. Kumar is 40 m to the right of Ankur.
ii. Dev is 60 m to the South of Kumar.
iii. NIlesh is 25 m to the West of Ankur.
iv. Pintu is 90 m to the North of Dev.
On a playing ground, Dev, Kumar, Nilesh, Ankur and Pintu are starting as directed below facing the North.
i. Kumar is 40 m to the right of Ankur.
ii. Dev is 60 m to the South of Kumar.
iii. NIlesh is 25 m to the West of Ankur.
iv. Pintu is 90 m to the North of Dev.
If a boy walks from Nilesh, meets Ankur followed by Kumar, Dev and then Pintu, how many metres has he walked, if he has travelled the straight distance all through?
a)
215 m
b)
155 m
c)
245 m
d)
185 m
|
|
Anaya Patel answered |
The correct option is A.
Required distance = 25 m + 40 m + 60 m + 90 m
Required distance = 215 m
Required distance = 25 m + 40 m + 60 m + 90 m
Required distance = 215 m
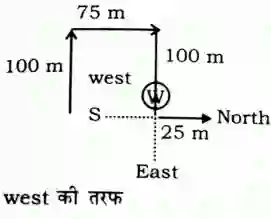
A man walks in straight 100 m and turns his right and walk 75 m. Again he turns his right and walk 100 m. And last he turn his left and walk 25m. If now he is walking in north di- rection. Then find from which direction he started?
- a)West
- b)East
- c)North
- d)South
Correct answer is option 'A'. Can you explain this answer?
A man walks in straight 100 m and turns his right and walk 75 m. Again he turns his right and walk 100 m. And last he turn his left and walk 25m. If now he is walking in north di- rection. Then find from which direction he started?
a)
West
b)
East
c)
North
d)
South

|
Vertex Academy answered |
Answer: (a)West
Solution:
Solution:
 \
\A man walks 1 km to East and then he turns to South and walks 5 km. Again he turns to East and walks 2 km. After this he turns to North and walks 9 km. Now, how far is he from his starting point?- a)3 km
- b)4 km
- c)5 km
- d)7 km
Correct answer is option 'C'. Can you explain this answer?
A man walks 1 km to East and then he turns to South and walks 5 km. Again he turns to East and walks 2 km. After this he turns to North and walks 9 km. Now, how far is he from his starting point?
a)
3 km
b)
4 km
c)
5 km
d)
7 km

|
Akanksha Dey answered |
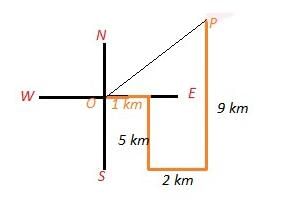
The last position of the man is P and OEP is a Right angled triangle in which
EP = 3 km and OE = 4 km
Thus,
OP = √(32 +42)
OP = √25
OP = 5 km.
EP = 3 km and OE = 4 km
Thus,
OP = √(32 +42)
OP = √25
OP = 5 km.
Hemant started from his house and walked 3km eastward, then he turned right and walked 2km, then again he turned left and walked 1 km, then turned right and walked 2 km. He turned right again and walked 1 km and reached his school. What is the minimum distance between Hemant’s house and his school?- a)12 km
- b)9km
- c)6 km
- d)5 km
Correct answer is option 'D'. Can you explain this answer?
Hemant started from his house and walked 3km eastward, then he turned right and walked 2km, then again he turned left and walked 1 km, then turned right and walked 2 km. He turned right again and walked 1 km and reached his school. What is the minimum distance between Hemant’s house and his school?
a)
12 km
b)
9km
c)
6 km
d)
5 km

|
Vertex Academy answered |
To solve this, let's break down Hemant's movements step by step and visualize his path:
- Hemant starts from his house and walks 3 km eastward.
- He turns right and walks 2 km south.
- He turns left and walks 1 km east.
- He turns right and walks 2 km south.
- He turns right and walks 1 km west and reaches his school.
Now, let's consider the overall east-west and north-south movement:
- East-West: Hemant initially walked 3 km east, then 1 km east, and finally 1 km west. So, the net eastward distance is 3 + 1 − 1 = 3 km.
- North-South: Hemant walked 2 km south, then another 2 km south, so he walked a total of 2 + 2 = 4 km south.
The minimum distance from Hemant’s house to the school can be found using the Pythagorean theorem (since he moved in perpendicular directions):
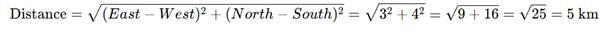
Thus, the minimum distance between Hemant’s house and his school is: D: 5 km
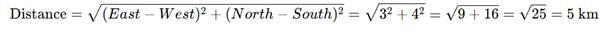
Thus, the minimum distance between Hemant’s house and his school is: D: 5 km
Starting from a point X Jayant walked 15 metres towards West, he turned to his left and walked 20 metres. He then turned to his left and walked 15 metres. He then further turned to his right and walked 12 metres. How far is Jayant from the point X and in which direction?- a)32 metres South
- b)47 metres East
- c)42 metres North
- d)27 metres South
Correct answer is option 'A'. Can you explain this answer?
Starting from a point X Jayant walked 15 metres towards West, he turned to his left and walked 20 metres. He then turned to his left and walked 15 metres. He then further turned to his right and walked 12 metres. How far is Jayant from the point X and in which direction?
a)
32 metres South
b)
47 metres East
c)
42 metres North
d)
27 metres South
|
|
Kiran Reddy answered |
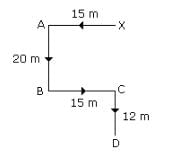
Required distance= 20 +12
= 32 m in south direction
= 32 m in south direction
A man is performing yoga with his head down and legs up. His face is towards the West. In which direction, will his left hand be?- a)North
- b)South
- c)East
- d)West
Correct answer is option 'A'. Can you explain this answer?
A man is performing yoga with his head down and legs up. His face is towards the West. In which direction, will his left hand be?
a)
North
b)
South
c)
East
d)
West

|
Avantika Chakraborty answered |
If you face towards west your left hand will be pointing towards the south when held straight side ways horizontally, now the person is upside down so obviously the direction of the left hand will be opposite, so it will be facing north direction.
Hemant started from his house and walked 3km eastward, then he turned right and walked 2km, then again he turned left and walked 1 km, then turned right and walked 2 km. He turned right again and walked 1 km and reached his school. What is the minimum distance between Hemant’s house and his school?- a)12 km
- b)9km
- c)6 km
- d)5 km
Correct answer is option 'D'. Can you explain this answer?
Hemant started from his house and walked 3km eastward, then he turned right and walked 2km, then again he turned left and walked 1 km, then turned right and walked 2 km. He turned right again and walked 1 km and reached his school. What is the minimum distance between Hemant’s house and his school?
a)
12 km
b)
9km
c)
6 km
d)
5 km
|
|
Faizan Khan answered |
Yes, the correct one is 5 Km
using pythagoras theoram.
using pythagoras theoram.
√3 ^2 + 4^ 2 = √9+16= √25
= 5 km is required answer
A starts from his house and moves towards B’s house which is 4km North. After walking for three-fourth of the distance he finds B coming towards him along with C, who is A’s enemy. Wanting to avoid him, A takes a left turn and runs for a distance of 2kms.Now, if from this point (say ‘P’) he decides to go to B’s house, how much distance would he need to cover?- a)3km
- b)Ö5km
- c)1km
- d)Ö3km
Correct answer is option 'B'. Can you explain this answer?
A starts from his house and moves towards B’s house which is 4km North. After walking for three-fourth of the distance he finds B coming towards him along with C, who is A’s enemy. Wanting to avoid him, A takes a left turn and runs for a distance of 2kms.Now, if from this point (say ‘P’) he decides to go to B’s house, how much distance would he need to cover?
a)
3km
b)
Ö5km
c)
1km
d)
Ö3km

|
Vertex Academy answered |
Let's analyze the path taken by A and the distances involved:
- A moves towards B's house: A starts moving north towards B's house which is 4 km away.
- A covers three-fourth of the distance: He covers 4 × 3/4 = 3 km towards the north.
- A takes a left turn: At this point, A is 1 km away from B's house (since he has covered 3 km out of 4 km). He then takes a left turn, which would be towards the west and runs 2 km.
Now, A is 1 km south of B's house and 2 km west of a direct line north from B’s house. To find the distance from point P (A's new location) to B's house, we use the Pythagorean theorem:

Thus, A would need to cover a distance of: B: √5km

Thus, A would need to cover a distance of: B: √5km
Namratha walks 14 metres towards west, then turns to her right and walks 14 meters and then turns to her left and walks 10 metres. Again turning to her left she walks 14 metres. What is the shortest distance (in metres) between her starting point and her present position?
- a)38m
- b)28m
- c)24m
- d)10m
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
Namratha walks 14 metres towards west, then turns to her right and walks 14 meters and then turns to her left and walks 10 metres. Again turning to her left she walks 14 metres. What is the shortest distance (in metres) between her starting point and her present position?
a)
38m
b)
28m
c)
24m
d)
10m
e)
None of these

|
Hridoy Das answered |
Let's break down Namratha's movements step by step:
- First Movement: She walks 14 meters west.
- Second Movement: She turns right and walks 14 meters north.
- Third Movement: She turns left and walks 10 meters west.
- Fourth Movement: She turns left again and walks 14 meters south.
Now, let's analyze her position.
- After the first movement, she's 14 meters west of the starting point.
- After the second movement, she's 14 meters west and 14 meters north of the starting point.
- After the third movement, she's 24 meters west and 14 meters north of the starting point.
- After the fourth movement, she moves 14 meters south, so she's now 24 meters west and at the same latitude as her starting point (because the south movement cancels out the north movement).
To find the shortest distance between her starting point and her present position, we just need to calculate the straight-line distance (which is the horizontal distance since her vertical displacement is zero).
Since she is 24 meters west of her starting point, the shortest distance is:
Distance=24 meters\text{Distance} = 24 \text{ meters}Distance=24 meters
So the correct answer is 24 meters (Option 3).
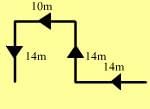
Hemant started from his house and walked 3km eastward, then he turned right and walked 2km, then again he turned left and walked 1 km, then turned right and walked 2 km. He turned right again and walked 1 km and reached his school. What is the minimum distance between Hemant’s house and his school?- a)12 km
- b)9km
- c)6 km
- d)3 km
- e)5 km
Correct answer is option 'E'. Can you explain this answer?
Hemant started from his house and walked 3km eastward, then he turned right and walked 2km, then again he turned left and walked 1 km, then turned right and walked 2 km. He turned right again and walked 1 km and reached his school. What is the minimum distance between Hemant’s house and his school?
a)
12 km
b)
9km
c)
6 km
d)
3 km
e)
5 km

|
Yatharth Pandey answered |
Yes correct one is 5 kms...as when you apply Pythagoras theoram...you will easily get the answer...(3)2+(4)2=√25= 5kms...
One morning after sunrise, Bikram and Shailash were standing in a town with their backs towards each other. Bikram’s shadow fell exactly towards left hand side. Which direction was Shailash facing?
- a)East
- b)West
- c)North
- d)South
Correct answer is option 'D'. Can you explain this answer?
One morning after sunrise, Bikram and Shailash were standing in a town with their backs towards each other. Bikram’s shadow fell exactly towards left hand side. Which direction was Shailash facing?
a)
East
b)
West
c)
North
d)
South

|
Nandini Gupta answered |
Sun rises in the East. It is given that "one morning after sunrise", therefore, we will mark Sun in the East direction in the below diagram.
When Sun is in the East direction, shadow of an object falls in the West.
It is given that Bikram's shadow falls towards left hand side. This means Bikram's left hand side should be West direction.
In the question above pattern followed is,
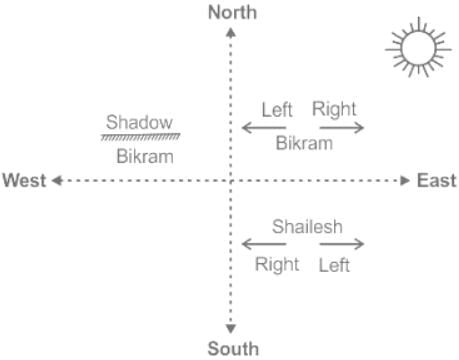
Therefore the correct answer is Option D South.

Therefore the correct answer is Option D South.
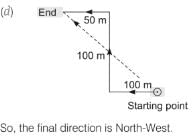
Raj starts from his office facing West and walks 100 m straight, then takes a right turn and walks 100 m. further, he takes a left turn and walks 50 m. In which direction is Raj now from the starting point?- a)North-East
- b)South-West
- c)North
- d)North-West
Correct answer is option 'D'. Can you explain this answer?
Raj starts from his office facing West and walks 100 m straight, then takes a right turn and walks 100 m. further, he takes a left turn and walks 50 m. In which direction is Raj now from the starting point?
a)
North-East
b)
South-West
c)
North
d)
North-West

|
Anjana Banerjee answered |
Rohan walked 40 metres towards North, took a left turn and walked 20 metres. He again took a left turn and walked 40 metres. The distance and the direction in which he is from the starting point is- a)20 metres East
- b)20 metres North
- c)20 metres West
- d)100 metres South
Correct answer is option 'C'. Can you explain this answer?
Rohan walked 40 metres towards North, took a left turn and walked 20 metres. He again took a left turn and walked 40 metres. The distance and the direction in which he is from the starting point is
a)
20 metres East
b)
20 metres North
c)
20 metres West
d)
100 metres South

|
EduRev GATE answered |
Given
1. Rohan walked 40 metres towards North, took a left turn and walked 20 metres.
2. He again took a left turn and walked 40 metres.
According to the given information, we get the following figure,
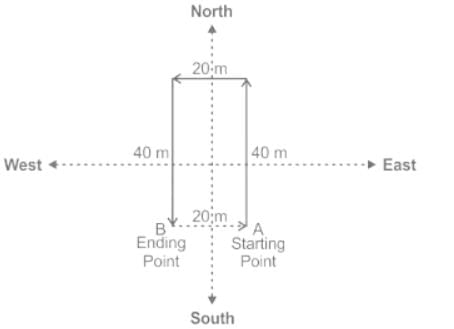
Therefore, above figure clearly shows the distance from B to A is 20 metres

Therefore, above figure clearly shows the distance from B to A is 20 metres
The direction of B with respect to A is West.
Hence, "20 metres West" is the correct answer.
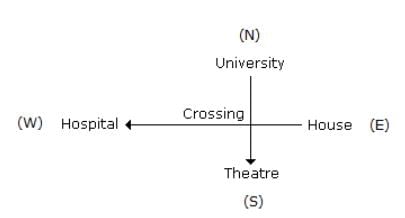
Sudha wants to go to the university and starts from her home which is in the East and comes to a crossing. The road to her left ends in a theatre. Straight ahead lies the hospital. In which direction is the university?- a)East
- b)West
- c)South
- d)North
Correct answer is option 'D'. Can you explain this answer?
Sudha wants to go to the university and starts from her home which is in the East and comes to a crossing. The road to her left ends in a theatre. Straight ahead lies the hospital. In which direction is the university?
a)
East
b)
West
c)
South
d)
North

|
Iq Funda answered |
To determine the direction of the university from Sudha's starting point:
- Sudha starts from her home, which is in the East.
- At the crossing, the road to the left leads to a theatre.
- Going straight ahead leads to a hospital.
- Considering these directions, the university must be in the North.
Tanuj started walking from a point ‘P’ towards South. After walking 40 metres he took a left turn. He then walked 30 metres and reached a point Q. What is the straight distance between P and Q and Q is towards in which direction with reference to point P? - a)60 metres, South-East
- b)50 metres, South-West
- c)50 metres, South-East
- d)Data Inadequate
Correct answer is option 'C'. Can you explain this answer?
Tanuj started walking from a point ‘P’ towards South. After walking 40 metres he took a left turn. He then walked 30 metres and reached a point Q. What is the straight distance between P and Q and Q is towards in which direction with reference to point P?
a)
60 metres, South-East
b)
50 metres, South-West
c)
50 metres, South-East
d)
Data Inadequate

|
Pk Academy answered |
Step 1: Tanuj starts from point P and walks 40 metres south.
Step 2: He takes a left turn (facing east) and walks 30 metres to reach point Q.
Applying the Pythagorean Theorem:
The path forms a right-angled triangle with:
One side = 40 metres (southward movement)
Another side = 30 metres (eastward movement)
Using the Pythagorean theorem to find the distance from P to Q:
PQ = √(40² + 30²) = √(1600 + 900) = √2500 = 50 metres
Direction of Q from P:
Since Tanuj moved south first and then east, Q is located South-East of P.
Answer:
c) 50 metres, South-East
Step 2: He takes a left turn (facing east) and walks 30 metres to reach point Q.
Applying the Pythagorean Theorem:
The path forms a right-angled triangle with:
One side = 40 metres (southward movement)
Another side = 30 metres (eastward movement)
Using the Pythagorean theorem to find the distance from P to Q:
PQ = √(40² + 30²) = √(1600 + 900) = √2500 = 50 metres
Direction of Q from P:
Since Tanuj moved south first and then east, Q is located South-East of P.
Answer:
c) 50 metres, South-East
Chapter doubts & questions for Distance & Direction - General Test Preparation for CUET UG 2025 is part of CUET Commerce exam preparation. The chapters have been prepared according to the CUET Commerce exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for CUET Commerce 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Distance & Direction - General Test Preparation for CUET UG in English & Hindi are available as part of CUET Commerce exam.
Download more important topics, notes, lectures and mock test series for CUET Commerce Exam by signing up for free.
General Test Preparation for CUET UG
194 videos|842 docs|2231 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup