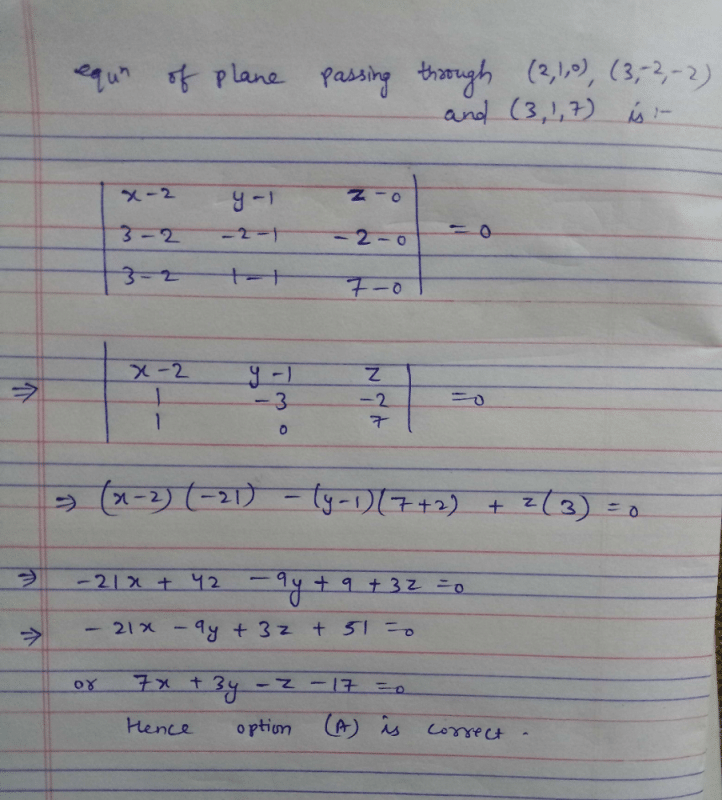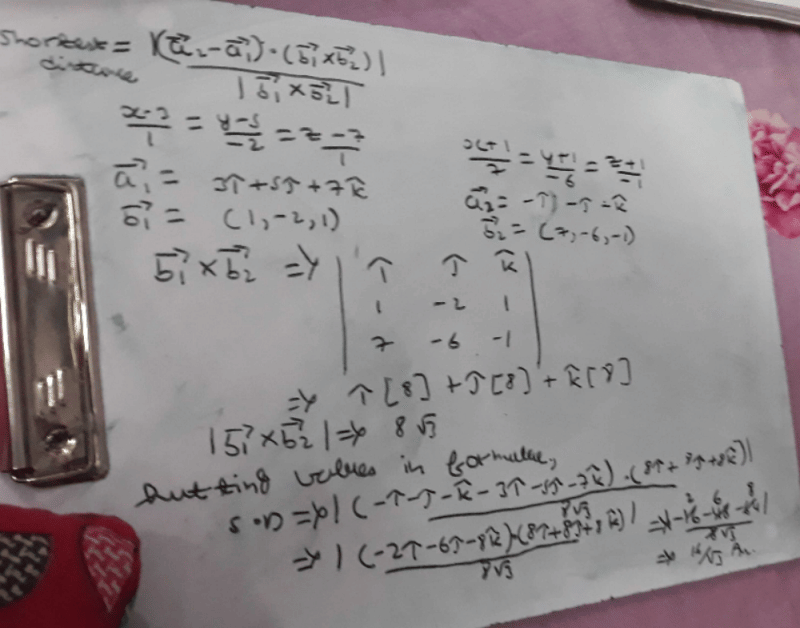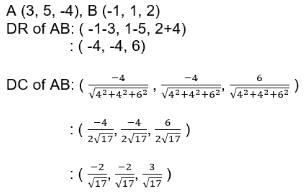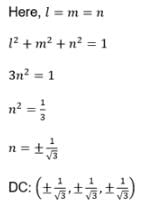All Exams >
JEE >
Mathematics CUET UG Mock Test Series 2026 >
All Questions
All questions of Chapter 11 - Three Dimensional Geometry for JEE Exam
Find the equation of the set of points which are equidistant from the points (1, 2 , 3) and (3, 2, -1)
a) x + 2z = 0
b) y + 2z = 0
c) x – 2z = 0
d) x – 2y = 0
Correct answer is option 'C'. Can you explain this answer?
|
Aryan Khanna answered |
Pt. A(1, 2 , 3)
Pt. B(3, 2, -1)
Let P(x,y,z)
So, AP = BP
((x-1)2 + (y-2)2 + (z-3)2)1/2 = ((x-3)2 + (y-2)2 + (z+1)2)1/2
(x-1)2 + (y-2)2 + (z-3)2) = (x-3)2 + (y-2)2 + (z+1)2
x2 +1 -2x + y2 + 4 - 4y + z2 + 9 – 6z = x2 +9 -6x + y2 + 4 - 4y + z2 + 1 + 2z
4x – 8z = 0
x – 2z = 0
Pt. B(3, 2, -1)
Let P(x,y,z)
So, AP = BP
((x-1)2 + (y-2)2 + (z-3)2)1/2 = ((x-3)2 + (y-2)2 + (z+1)2)1/2
(x-1)2 + (y-2)2 + (z-3)2) = (x-3)2 + (y-2)2 + (z+1)2
x2 +1 -2x + y2 + 4 - 4y + z2 + 9 – 6z = x2 +9 -6x + y2 + 4 - 4y + z2 + 1 + 2z
4x – 8z = 0
x – 2z = 0
The direction cosines of the line joining the points (2, -1, 8) and (-4, -3, 5) are:- a)
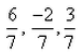
- b)
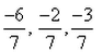
- c)
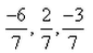
- d)
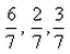
Correct answer is option 'B'. Can you explain this answer?
The direction cosines of the line joining the points (2, -1, 8) and (-4, -3, 5) are:
a)
b)
c)
d)
|
Geetika Shah answered |
Pt. A(2, -1, 8)
Pt. B(-4, -3, 5)
Direction Ratio DR of AB : ( -4-2 , -3+1 , 5-8 )
: (-6,-2,-3)
Direction cosine of AB : ( -6/(62+22+32)1/2 , -2/(62+22+32)1/2 , -3/(62+22+32)1/2)
: ( -6/7, -2/7, -3/7)
Pt. B(-4, -3, 5)
Direction Ratio DR of AB : ( -4-2 , -3+1 , 5-8 )
: (-6,-2,-3)
Direction cosine of AB : ( -6/(62+22+32)1/2 , -2/(62+22+32)1/2 , -3/(62+22+32)1/2)
: ( -6/7, -2/7, -3/7)
The signs of the X,Y and Z coordinates of a point that lies in the octant OXYZ’ is- a)(- , + , +)
- b)(-, – , +)
- c)( + , – , -)
- d)( + , + , -)
Correct answer is option 'D'. Can you explain this answer?
The signs of the X,Y and Z coordinates of a point that lies in the octant OXYZ’ is
a)
(- , + , +)
b)
(-, – , +)
c)
( + , – , -)
d)
( + , + , -)
|
Vikas Kapoor answered |
X,Y,Z imply positive X,Y,Z axis & X’,Y’,Z’ imply negative X,Y,Z axis.
So, OXYZ’ will have a point of signs (+, +, -).
So, OXYZ’ will have a point of signs (+, +, -).
The distance of the point (2, 3, – 5) from the plane x + 2y – 2z = 9 is:- a)2 units
- b)3/2 units
- c)3 units
- d)10/3 units
Correct answer is option 'C'. Can you explain this answer?
The distance of the point (2, 3, – 5) from the plane x + 2y – 2z = 9 is:
a)
2 units
b)
3/2 units
c)
3 units
d)
10/3 units
|
Nikita Singh answered |
Length of perpendicular from (2,3,-5) to the plane x + 2y − 2z − 9 = 0.
= |(2 + 2×3 −2×(−5) − 9)|√12 + 22 + (−2)2
= |2 + 6 + 10 − 9|/√9
= 9/3
= 3 units.
= |(2 + 2×3 −2×(−5) − 9)|√12 + 22 + (−2)2
= |2 + 6 + 10 − 9|/√9
= 9/3
= 3 units.
The equation of the plane passing through the intersection of the planes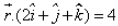 
and 
and 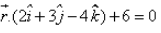the point (1, 2, 1) is:- a)18x+6y+14z-23=0
- b)18x+7y+14z-46=0
- c)9x+3y+7z-23=0
- d)18x+7y+14z-38=0
Correct answer is option 'B'. Can you explain this answer?
The equation of the plane passing through the intersection of the planes 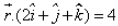and and 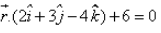the point (1, 2, 1) is:
and and the point (1, 2, 1) is:a)
18x+6y+14z-23=0
b)
18x+7y+14z-46=0
c)
9x+3y+7z-23=0
d)
18x+7y+14z-38=0
|
|
Aryan Khanna answered |
n1 = 2i + j + k
n2 = 2i + 3j - 4k
p1 = 4, p2 = -6
r.(n1 + λn2) = p1 + λp2
=> r . [2i + j + k + λ(2i + 3j - 4k)] = 4 - 6λ
=> r . [ i(2 + 2λ) + j(1 + 3λ) + k(1 - 4k)] = 4 - 6λ
Taking r = xi + yj + zk
(2 + 2λ)x + (1 + 3λ)y + (1 - 4k)z = 4 - 6λ
(2x + y + - z - 4) + λ(2x + 3y - 4k + 6) = 0
Given points are (1,2,1)
(2 + 2 - 1 - 4) + λ(2 + 6 - 4 + 6) = 0
-1 + λ(10) = 0
λ = 1/10
Substitute λ = 1/10, we get
18x + 7y + 14z - 46=0
n2 = 2i + 3j - 4k
p1 = 4, p2 = -6
r.(n1 + λn2) = p1 + λp2
=> r . [2i + j + k + λ(2i + 3j - 4k)] = 4 - 6λ
=> r . [ i(2 + 2λ) + j(1 + 3λ) + k(1 - 4k)] = 4 - 6λ
Taking r = xi + yj + zk
(2 + 2λ)x + (1 + 3λ)y + (1 - 4k)z = 4 - 6λ
(2x + y + - z - 4) + λ(2x + 3y - 4k + 6) = 0
Given points are (1,2,1)
(2 + 2 - 1 - 4) + λ(2 + 6 - 4 + 6) = 0
-1 + λ(10) = 0
λ = 1/10
Substitute λ = 1/10, we get
18x + 7y + 14z - 46=0
The angle between the lines x = 2y = – 3z and – 4x = 6y = – z is:- a)0°
- b)cos-1(1/√3)
- c)90°
- d)180°
Correct answer is option 'C'. Can you explain this answer?
The angle between the lines x = 2y = – 3z and – 4x = 6y = – z is:
a)
0°
b)
cos-1(1/√3)
c)
90°
d)
180°
|
Sushil Kumar answered |
x = 2y = -3z -4x = 6y = -z
x/1 = y/(½) = z(-⅓) x/(-¼) = y/(⅙) = z/(-1)
Cosθ = [(a1a2 + b1b2 + c1c2)/(a1 + b1 + c1)½ * (a2 + b2 + c2)½]
Cosθ ={[(1*(-¼)) + (½)(⅙) + (-⅓)(-1)]/[(1)2 + (½)2 + (-⅓)2]1/2 * [(-¼)2 + (⅙)2 + (-1)2]1/2}
= {[(-¼ + 1/12 - ⅓)]/[2 + 1 - ⅔]1/2 * [ -½ + ⅓ -½]½}
Cosθ = 0
θ = 90deg
x/1 = y/(½) = z(-⅓) x/(-¼) = y/(⅙) = z/(-1)
Cosθ = [(a1a2 + b1b2 + c1c2)/(a1 + b1 + c1)½ * (a2 + b2 + c2)½]
Cosθ ={[(1*(-¼)) + (½)(⅙) + (-⅓)(-1)]/[(1)2 + (½)2 + (-⅓)2]1/2 * [(-¼)2 + (⅙)2 + (-1)2]1/2}
= {[(-¼ + 1/12 - ⅓)]/[2 + 1 - ⅔]1/2 * [ -½ + ⅓ -½]½}
Cosθ = 0
θ = 90deg
If a line has the direction ratios -4, 18, -12 then what are its direction cosines?- a)-2, 9, -6
- b)-4, 18, -12
- c)2/11, 9/11, 6/11
- d)-2/11, 9/11, -6/11
Correct answer is option 'D'. Can you explain this answer?
If a line has the direction ratios -4, 18, -12 then what are its direction cosines?
a)
-2, 9, -6
b)
-4, 18, -12
c)
2/11, 9/11, 6/11
d)
-2/11, 9/11, -6/11
|
|
Vikas Kapoor answered |
DR of the line : (-4, 18 -12)
DC of the line : (-4/k, 18/k, -12/k)
where k = ((42) + (182) + (12)2)1/2
= (16 + 324 + 144)1/2
= (484)1/2
= 22
So, DC : (-4/22, 18/22, -12/22)
: (-2/11 , 9/11 , -6/11)
DC of the line : (-4/k, 18/k, -12/k)
where k = ((42) + (182) + (12)2)1/2
= (16 + 324 + 144)1/2
= (484)1/2
= 22
So, DC : (-4/22, 18/22, -12/22)
: (-2/11 , 9/11 , -6/11)
The equation of the plane passing through the line of intersection of the planes x-2y+3z+8=0 and 2x-7y+4z-3=0 and the point (3, 1, -2) is:- a)6x-15y+12z+29=0
- b)6x-15y+16z+29=0
- c)6x-15y+12z+32=0
- d)2x-5y+4z+9=0
Correct answer is option 'B'. Can you explain this answer?
The equation of the plane passing through the line of intersection of the planes x-2y+3z+8=0 and 2x-7y+4z-3=0 and the point (3, 1, -2) is:
a)
6x-15y+12z+29=0
b)
6x-15y+16z+29=0
c)
6x-15y+12z+32=0
d)
2x-5y+4z+9=0
|
Tejas Verma answered |
(x - 2y + 3z + 8) + μ(2x - 7y + 4z - 3) = 0
i.e, (1 + 2μ)x - (2 + 7μ)y + (3 + 4μ)z + (8 - 3μ) = 0......(1)
the required plane is passing through (3, 1, -2)
so, 3(1 + 2μ) - (1)(2 + 7μ) + (-2)(3 + 4μ)+ (8 - 3μ) = 0
3 + 6μ - 2 - 7μ -6 -8μ + 8 - 3μ = 0
by solving, μ = 1/4
putting μ in equation (1)
we get the required equation of plane as :- 6x - 15y + 16z + 29 = 0
i.e, (1 + 2μ)x - (2 + 7μ)y + (3 + 4μ)z + (8 - 3μ) = 0......(1)
the required plane is passing through (3, 1, -2)
so, 3(1 + 2μ) - (1)(2 + 7μ) + (-2)(3 + 4μ)+ (8 - 3μ) = 0
3 + 6μ - 2 - 7μ -6 -8μ + 8 - 3μ = 0
by solving, μ = 1/4
putting μ in equation (1)
we get the required equation of plane as :- 6x - 15y + 16z + 29 = 0
and 
is:
The Cartesian form of the equation of the plane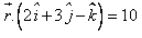 
is:- a)2x+3y-z=10
- b)2x+3y-z= √14
- c)2x+3y-z+√14=0
- d)2x+3y-z+10=0
Correct answer is option 'A'. Can you explain this answer?
The Cartesian form of the equation of the plane 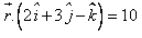is:
is:a)
2x+3y-z=10
b)
2x+3y-z= √14
c)
2x+3y-z+√14=0
d)
2x+3y-z+10=0
|
Deepak Kapoor answered |
Let r = xi + yj + zk
(xi + yj + zk) . (2i + 3j - k) = 10
2x + 3y - k = 10
If a line makes angles 45°,150°, 135°, with x, y and z-axes respectively, find its direction cosines.- a)
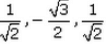
- b)
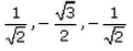
- c)
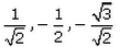
- d)
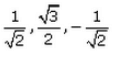
Correct answer is option 'B'. Can you explain this answer?
If a line makes angles 45°,150°, 135°, with x, y and z-axes respectively, find its direction cosines.
a)
b)
c)
d)
|
|
Leelu Bhai answered |
Direction cosines of this line are cos 45, cos150
The length of the perpendicular from the origin to the plane 3x + 2y – 6z = 21 is:- a)3
- b)14
- c)21
- d)7
Correct answer is option 'A'. Can you explain this answer?
The length of the perpendicular from the origin to the plane 3x + 2y – 6z = 21 is:
a)
3
b)
14
c)
21
d)
7
|
|
Leelu Bhai answered |
Given equation of plane is : 3x + 2y - 6z - 21= 0
the length of perpendicular from a given point
(x' , y', z') on a plane ax + by + cz + d = 0 is given as :-
d = modulus of [{ax' + by' + cz' + d}/{√(a² + b² + c)²}]
so, d = modulus of [{(3*0) + (2*0) + (-6*0) + (-21)}/{√(3² + 2² + (-6)²)}]
d= modulus of (-21/√49) = (-21/7) = 3 units
hence option A is correct....
the length of perpendicular from a given point
(x' , y', z') on a plane ax + by + cz + d = 0 is given as :-
d = modulus of [{ax' + by' + cz' + d}/{√(a² + b² + c)²}]
so, d = modulus of [{(3*0) + (2*0) + (-6*0) + (-21)}/{√(3² + 2² + (-6)²)}]
d= modulus of (-21/√49) = (-21/7) = 3 units
hence option A is correct....
The equation of the plane passing through the point (3, – 3, 1) and perpendicular to the line joining the points (3, 4, – 1) and (2, – 1, 5) is:- a)– x – 5y + 6z + 18 = 0
- b)x – 5y + 6z + 18 = 0
- c)x + 5y – 6z + 18 = 0
- d)– x – 5y – 6z + 18 = 0
Correct answer is 'C'. Can you explain this answer?
The equation of the plane passing through the point (3, – 3, 1) and perpendicular to the line joining the points (3, 4, – 1) and (2, – 1, 5) is:
a)
– x – 5y + 6z + 18 = 0
b)
x – 5y + 6z + 18 = 0
c)
x + 5y – 6z + 18 = 0
d)
– x – 5y – 6z + 18 = 0
|
|
Leelu Bhai answered |
The equation of plane through the intersection of planes (x+y+z =1) and (2x +3y – z+4) =0 is- a)x(1 + 2k) + y(1 + 3k) + z(1 – k) + (-1 + 4k) = 0
- b)x(1+2k)+y(1-3k)+z(1-k)+(-1+4k) = 0
- c)x(1+2k) +y(1+3k)+z(1-k) +(-1 – 4k) = 0
- d)x (1-2k) + y(1+3k) +z(1-k) +(-1+4k) = 0
Correct answer is option 'A'. Can you explain this answer?
The equation of plane through the intersection of planes (x+y+z =1) and (2x +3y – z+4) =0 is
a)
x(1 + 2k) + y(1 + 3k) + z(1 – k) + (-1 + 4k) = 0
b)
x(1+2k)+y(1-3k)+z(1-k)+(-1+4k) = 0
c)
x(1+2k) +y(1+3k)+z(1-k) +(-1 – 4k) = 0
d)
x (1-2k) + y(1+3k) +z(1-k) +(-1+4k) = 0
|
Kritika Sarkar answered |
To find the equation of the plane through the intersection of two given planes, we need to first determine the line of intersection and then find a normal vector for the plane.
1. Finding the line of intersection:
The two given planes are:
Plane 1: x + y + z = 1
Plane 2: 2x + 3y + z + 4 = 0
To find the line of intersection, we can set the equations of the two planes equal to each other:
x + y + z = 1
2x + 3y + z + 4 = 0
By subtracting the second equation from the first equation, we can eliminate z:
x + y + z - (2x + 3y + z + 4) = 1 - 0
-x - 2y - 4 = -1
Simplifying the equation, we get:
x + 2y = 3
This equation represents the line of intersection of the two planes.
2. Finding a normal vector for the plane:
Since the line of intersection lies on both planes, the normal vector of the required plane should be perpendicular to this line. Therefore, we can choose the direction ratios of the line, -1 and 2, as coefficients of the normal vector.
The normal vector of the required plane is given by the cross product of the direction ratios of the line of intersection:
n = (1, 2, 0) x (-1, 2, 0) = (0, 0, -4)
3. Writing the equation of the plane:
Now we have a point on the plane, (1, 0, 0), and a normal vector, (0, 0, -4). We can use the point-normal form of the equation of a plane to write the equation of the required plane.
The equation of the plane is given by:
0(x - 1) + 0(y - 0) + (-4)(z - 0) = 0
Simplifying the equation, we get:
-4z + 4 = 0
z = 1
Therefore, the equation of the plane through the intersection of the given planes is:
x + 2y - 4z + 4 = 0
Comparing this equation with the options provided, we see that option A is the correct answer:
x(1 2k) + y(1 3k) + z(1 k) + (-1 4k) = 0
1. Finding the line of intersection:
The two given planes are:
Plane 1: x + y + z = 1
Plane 2: 2x + 3y + z + 4 = 0
To find the line of intersection, we can set the equations of the two planes equal to each other:
x + y + z = 1
2x + 3y + z + 4 = 0
By subtracting the second equation from the first equation, we can eliminate z:
x + y + z - (2x + 3y + z + 4) = 1 - 0
-x - 2y - 4 = -1
Simplifying the equation, we get:
x + 2y = 3
This equation represents the line of intersection of the two planes.
2. Finding a normal vector for the plane:
Since the line of intersection lies on both planes, the normal vector of the required plane should be perpendicular to this line. Therefore, we can choose the direction ratios of the line, -1 and 2, as coefficients of the normal vector.
The normal vector of the required plane is given by the cross product of the direction ratios of the line of intersection:
n = (1, 2, 0) x (-1, 2, 0) = (0, 0, -4)
3. Writing the equation of the plane:
Now we have a point on the plane, (1, 0, 0), and a normal vector, (0, 0, -4). We can use the point-normal form of the equation of a plane to write the equation of the required plane.
The equation of the plane is given by:
0(x - 1) + 0(y - 0) + (-4)(z - 0) = 0
Simplifying the equation, we get:
-4z + 4 = 0
z = 1
Therefore, the equation of the plane through the intersection of the given planes is:
x + 2y - 4z + 4 = 0
Comparing this equation with the options provided, we see that option A is the correct answer:
x(1 2k) + y(1 3k) + z(1 k) + (-1 4k) = 0
The angle of the line through Z-axis is:
Direction: Read the following text and answer the following questions on the basis of the same:A mobile tower stands at the top of a hill. Consider the surface on which the tower stands as a plane having points A(1, 0, 2), B(3, –1, 1) and C(1, 2, 1) on it. The mobile tower is tied with 3 cables from the points A, B and C such that it stands vertically on the ground. The top of the tower is at the point (2, 3, 1) as shown in the figure.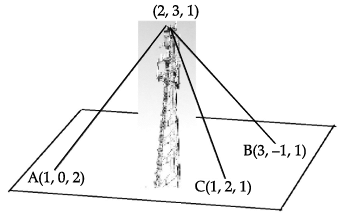
Q. The equation of the plane passing through the points A, B and C is- a)3x – 2y + 4z = –11
- b)3x + 2y + 4z = 11
- c)3x – 2y – 4z = 11
- d)–3x + 2y + 4z = –11
Correct answer is option 'B'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
A mobile tower stands at the top of a hill. Consider the surface on which the tower stands as a plane having points A(1, 0, 2), B(3, –1, 1) and C(1, 2, 1) on it. The mobile tower is tied with 3 cables from the points A, B and C such that it stands vertically on the ground. The top of the tower is at the point (2, 3, 1) as shown in the figure.
Q. The equation of the plane passing through the points A, B and C is
a)
3x – 2y + 4z = –11
b)
3x + 2y + 4z = 11
c)
3x – 2y – 4z = 11
d)
–3x + 2y + 4z = –11
|
Krishna Iyer answered |
A(1, 0, 2), B(3, –1, 1) and C(1, 2, 1)
(x - 1)(1 + 2) -y (-2, 0) + (z - 2) (4 - 0)
3x - 3 + 2y + 4z - 8 = 0
3x + 2y + 4z = 11
If the vector equation of a line is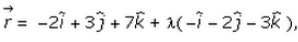 
find its caryesian equation.- a)
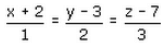
- b)
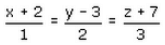
- c)
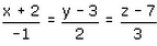
- d)
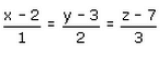
Correct answer is option 'A'. Can you explain this answer?
If the vector equation of a line is 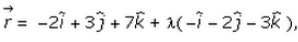find its caryesian equation.
find its caryesian equation.a)
b)
c)
d)
|
|
Gaurav Kumar answered |
r = -2i + 3j + 7k + λ( -i - 2j - 3k)
xi + yj + zk = (-2-λ)i + (3-2λ)j + (7-3λ)k
Equating the terms, we get
x = -2-λ y = 3-2λ z = 7-3λ
(x+2)/(-1) = λ, (y-3)/(-2) = λ, (z-7)/(-3) = λ
(x+2)/(1) = (y-3)/(2) = (z-7)/(3)
xi + yj + zk = (-2-λ)i + (3-2λ)j + (7-3λ)k
Equating the terms, we get
x = -2-λ y = 3-2λ z = 7-3λ
(x+2)/(-1) = λ, (y-3)/(-2) = λ, (z-7)/(-3) = λ
(x+2)/(1) = (y-3)/(2) = (z-7)/(3)
Find the direction cosines of the x axis.- a)1, 0, 0
- b)0, 0, 0
- c)0, 1, 0
- d)0, 0, 1
Correct answer is option 'A'. Can you explain this answer?
Find the direction cosines of the x axis.
a)
1, 0, 0
b)
0, 0, 0
c)
0, 1, 0
d)
0, 0, 1
|
Ishan Choudhury answered |
To find Direction Cosines of X-axis.
Take any two points on X-axis : A(a,0,0) & B(b,0,0)
DR of AB : (b-a,0,0)
DC of AB : ((b-a)/(((b-a)2 + 0 + 0)1/2), 0, 0)
: ((b-a)/(b-a) , 0 , 0)
: (1,0,0)
Take any two points on X-axis : A(a,0,0) & B(b,0,0)
DR of AB : (b-a,0,0)
DC of AB : ((b-a)/(((b-a)2 + 0 + 0)1/2), 0, 0)
: ((b-a)/(b-a) , 0 , 0)
: (1,0,0)
and 
is:
In the following case, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them. 2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z – 1 = 0- a)The planes are perpendicular
- b)The planes are parallel
- c)The planes are at 45∘
- d)The planes are at 55∘
Correct answer is option 'B'. Can you explain this answer?
In the following case, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them. 2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z – 1 = 0
a)
The planes are perpendicular
b)
The planes are parallel
c)
The planes are at 45∘
d)
The planes are at 55∘
|
Pranavi Iyer answered |
The equation of the plane, which is at a distance of 5 unit from the origin and has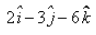 
as a normal vector, is:- a)
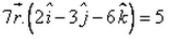
- b)
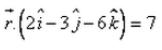
- c)
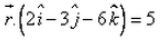
- d)
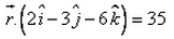
Correct answer is option 'D'. Can you explain this answer?
The equation of the plane, which is at a distance of 5 unit from the origin and has 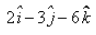as a normal vector, is:
as a normal vector, is:a)
b)
c)
d)
|
Preeti Iyer answered |
x = 3i - 2j - 6k
|x| = ((3)2 + (2)2 + (6)2)
|x| = (49)½
|x| = 7
x = x/|x|
= (3i - 2j - 6k)/7
The required equation of plane is r.x = d
⇒ r.(3i - 2j - 6k)/7 = 5
⇒ r.(3i - 2j - 6k) = 35
|x| = ((3)2 + (2)2 + (6)2)
|x| = (49)½
|x| = 7
x = x/|x|
= (3i - 2j - 6k)/7
The required equation of plane is r.x = d
⇒ r.(3i - 2j - 6k)/7 = 5
⇒ r.(3i - 2j - 6k) = 35
For which value of a lines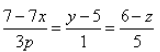 
and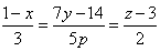 
are perpendicular?
- a)11/70
- b)5
- c)1
- d)70/11
Correct answer is option 'B'. Can you explain this answer?
For which value of a lines 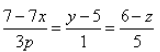and are perpendicular?
and 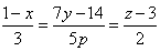are perpendicular?a)
11/70
b)
5
c)
1
d)
70/11
|
|
Tejas Verma answered |
(x-1)/(-3) = (y-2)/(2p/7) = (z-3)/2
(x-1)(-3p/7) = (y - 5)/1 = (z - 6)/(-5)
The direction ratio of the line are -3, 2p/7, -2 and (-3p)/7, 1, -5
Two lines with direction ratios, a1, b1, c1 and a2, b2, c2 are perpendicular to each other if a1a2 + b1b2 + c1c2 = 0
Therefore, (-3)(-3p/7) + (2p/7)(1) + 2(-5) = 0
(9p/7) + (2p/7) = 10
11p = 70
p = 70/1
(x-1)(-3p/7) = (y - 5)/1 = (z - 6)/(-5)
The direction ratio of the line are -3, 2p/7, -2 and (-3p)/7, 1, -5
Two lines with direction ratios, a1, b1, c1 and a2, b2, c2 are perpendicular to each other if a1a2 + b1b2 + c1c2 = 0
Therefore, (-3)(-3p/7) + (2p/7)(1) + 2(-5) = 0
(9p/7) + (2p/7) = 10
11p = 70
p = 70/1
The equation of the plane passing through the point (3, – 3, 1) and perpendicular to the line joining the points (3, 4, – 1) and (2, – 1, 5) is:- a)– x – 5y + 6z + 18 = 0
- b)x – 5y + 6z + 18 = 0
- c)x + 5y – 6z + 18 = 0
- d)– x – 5y – 6z + 18 = 0
Correct answer is option 'C'. Can you explain this answer?
The equation of the plane passing through the point (3, – 3, 1) and perpendicular to the line joining the points (3, 4, – 1) and (2, – 1, 5) is:
a)
– x – 5y + 6z + 18 = 0
b)
x – 5y + 6z + 18 = 0
c)
x + 5y – 6z + 18 = 0
d)
– x – 5y – 6z + 18 = 0
|
|
Preeti Iyer answered |
The equation of the plane passing through the point (3, – 3, 1) is:
a(x – 3) + b(y + 3) + c(z – 1) = 0 and the direction ratios of the line joining the points
(3, 4, – 1) and (2, – 1, 5) is 2 – 3, – 1 – 4, 5 + 1, i.e., – 1, – 5, 6.
Since the plane is perpendicular to the line whose direction ratios are – 1, – 5, 6, therefore, direction ratios of the normal to the plane is – 1, – 5, 6.
So, required equation of plane is: – 1(x – 3) – 5(y + 3) + 6(z – 1) = 0
i.e., x + 5y – 6z + 18 = 0.
a(x – 3) + b(y + 3) + c(z – 1) = 0 and the direction ratios of the line joining the points
(3, 4, – 1) and (2, – 1, 5) is 2 – 3, – 1 – 4, 5 + 1, i.e., – 1, – 5, 6.
Since the plane is perpendicular to the line whose direction ratios are – 1, – 5, 6, therefore, direction ratios of the normal to the plane is – 1, – 5, 6.
So, required equation of plane is: – 1(x – 3) – 5(y + 3) + 6(z – 1) = 0
i.e., x + 5y – 6z + 18 = 0.
and 
is:
If a line in the ZX-plane makes an angle 60o with Z-axis, the direction cosines of this line are:- a)
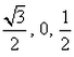
- b)
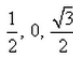
- c)
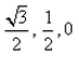
- d)
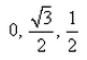
Correct answer is option 'A'. Can you explain this answer?
If a line in the ZX-plane makes an angle 60o with Z-axis, the direction cosines of this line are:
a)
b)
c)
d)
|
Saumya Gupta answered |
The angle between the line and z axis is 60 and the line in ZX plane so the angle between line and X axis is (90-60)=30 and line is perpendicular to Y axis so the angle between line and Y axis is 90. So direction cosine of line is cos30,cos90,cos60 =√3/2,0,1/2.
Direction: Read the following text and answer the following questions on the basis of the same:The Indian coast guard, while patrolling, saw a suspicious boat with people. They were nowhere looking like fishermen. The coast guard were closely observing the movement of the boat for an opportunity to seize the boat. They observed that the boat is moving along a planar surface. At an instant of time, the coordinates of the position of the coast guard helicopter and the boat is (1, 3, 5) and (2, 5, 3) respectively.
Q. If the coast guard decides to shoot the boat at that given instant of time, when the speed of bullet is 36 m/sec, then what is the time taken for the bullet to travel and hit the boat?- a)1/8 second
- b)1/14 second
- c)1/10 second
- d)1/12 second
Correct answer is option 'D'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
The Indian coast guard, while patrolling, saw a suspicious boat with people. They were nowhere looking like fishermen. The coast guard were closely observing the movement of the boat for an opportunity to seize the boat. They observed that the boat is moving along a planar surface. At an instant of time, the coordinates of the position of the coast guard helicopter and the boat is (1, 3, 5) and (2, 5, 3) respectively.
Q. If the coast guard decides to shoot the boat at that given instant of time, when the speed of bullet is 36 m/sec, then what is the time taken for the bullet to travel and hit the boat?
a)
1/8 second
b)
1/14 second
c)
1/10 second
d)
1/12 second
|
|
Nandini Iyer answered |
Time taken for the bullet to travel and hit the boat
In the following case, determine whether the given planes are parallel orperpendicular, and in case they are neither, find the angles between them. 2x + y + 3z – 2 = 0 and x – 2y + 5 = 0- a)The planes are parallel
- b)The planes are at 45∘
- c)The planes are at 55∘
- d)The planes are perpendicular
Correct answer is option 'D'. Can you explain this answer?
In the following case, determine whether the given planes are parallel orperpendicular, and in case they are neither, find the angles between them. 2x + y + 3z – 2 = 0 and x – 2y + 5 = 0
a)
The planes are parallel
b)
The planes are at 45∘
c)
The planes are at 55∘
d)
The planes are perpendicular
|
Upasana Nambiar answered |
Understanding the Given Planes
To determine the relationship between the two planes, we need to first rewrite their equations in a standard format and extract the normal vectors.
Plane Equations
1. First Plane:
The equation is given as 2x + y + 3z - 2 = 0.
The normal vector (N1) can be derived from the coefficients:
N1 = (2, 1, 3).
2. Second Plane:
The equation is x - 2y + 5 = 0, which can be rewritten as x - 2y + 0z + 5 = 0.
The normal vector (N2) can be derived as:
N2 = (1, -2, 0).
Checking for Parallelism
- Two planes are parallel if their normal vectors are scalar multiples of each other.
- Here, N1 = (2, 1, 3) and N2 = (1, -2, 0) are not scalar multiples.
- Thus, the planes are not parallel.
Checking for Perpendicularity
- Two planes are perpendicular if the dot product of their normal vectors equals zero.
- We calculate the dot product:
N1 • N2 = (2)(1) + (1)(-2) + (3)(0) = 2 - 2 + 0 = 0.
- Since the dot product is zero, the planes are perpendicular.
Conclusion
The given planes are neither parallel nor at a specified angle; they are indeed perpendicular to each other. Thus, the correct answer is option 'D'.
To determine the relationship between the two planes, we need to first rewrite their equations in a standard format and extract the normal vectors.
Plane Equations
1. First Plane:
The equation is given as 2x + y + 3z - 2 = 0.
The normal vector (N1) can be derived from the coefficients:
N1 = (2, 1, 3).
2. Second Plane:
The equation is x - 2y + 5 = 0, which can be rewritten as x - 2y + 0z + 5 = 0.
The normal vector (N2) can be derived as:
N2 = (1, -2, 0).
Checking for Parallelism
- Two planes are parallel if their normal vectors are scalar multiples of each other.
- Here, N1 = (2, 1, 3) and N2 = (1, -2, 0) are not scalar multiples.
- Thus, the planes are not parallel.
Checking for Perpendicularity
- Two planes are perpendicular if the dot product of their normal vectors equals zero.
- We calculate the dot product:
N1 • N2 = (2)(1) + (1)(-2) + (3)(0) = 2 - 2 + 0 = 0.
- Since the dot product is zero, the planes are perpendicular.
Conclusion
The given planes are neither parallel nor at a specified angle; they are indeed perpendicular to each other. Thus, the correct answer is option 'D'.
Direction: Read the following text and answer the following questions on the basis of the same:A cricket match is organized between two Clubs A and B for which a team from each club is chosen. Remaining players of Club A and Club B are respectively sitting on the plane represented by the equation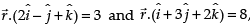 
to cheer the team of their own clubs.
Q. The intercept form of the equation of the plane on which players of Club B are seated is- a)
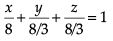
- b)
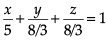
- c)
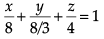
- d)
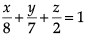
Correct answer is option 'C'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
A cricket match is organized between two Clubs A and B for which a team from each club is chosen. Remaining players of Club A and Club B are respectively sitting on the plane represented by the equation 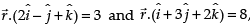to cheer the team of their own clubs.
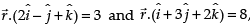to cheer the team of their own clubs.Q. The intercept form of the equation of the plane on which players of Club B are seated is
a)
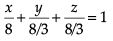
b)
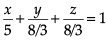
c)
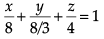
d)
|
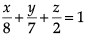
Hansa Sharma answered |
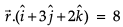
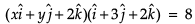
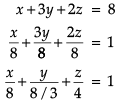
Find the equations of the planes that passes through three points (1, 1, 0), (1, 2, 1), (– 2, 2, – 1)- a)2x + 3y – 7z = 5
- b)2x + 5y – 3z = 5
- c)3x + 3y – 3z = 5
- d)2x + 3y – 3z = 5
Correct answer is option 'D'. Can you explain this answer?
Find the equations of the planes that passes through three points (1, 1, 0), (1, 2, 1), (– 2, 2, – 1)
a)
2x + 3y – 7z = 5
b)
2x + 5y – 3z = 5
c)
3x + 3y – 3z = 5
d)
2x + 3y – 3z = 5
|
Anand Khanna answered |
In cartesian co-ordinate system :
Equation of a plane passing through three non collinear
Equation of a plane passing through three non collinear
Points (x1, y1, z1) , (x2, y2, z2) and (x3, y3, z3) is given by :
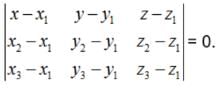
Therefore, the equations of the planes that passes through three points (1,1,0), (1,2,1), (-2,2,-1) is given by :
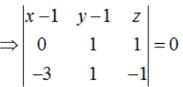
⇒ (x-1)(-2) - (y-1) (3) + 3z = 0
⇒ 2x+3y - 3z = 5
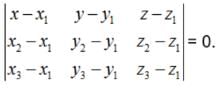
Therefore, the equations of the planes that passes through three points (1,1,0), (1,2,1), (-2,2,-1) is given by :
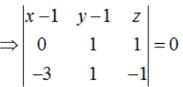
⇒ (x-1)(-2) - (y-1) (3) + 3z = 0
⇒ 2x+3y - 3z = 5
Find the equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0.- a)x + z + 2 = 0
- b)– x – z + 2 = 0
- c)x – z + 2 = 0
- d)x + z + 5 = 0
Correct answer is option 'C'. Can you explain this answer?
Find the equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0.
a)
x + z + 2 = 0
b)
– x – z + 2 = 0
c)
x – z + 2 = 0
d)
x + z + 5 = 0
|
Avi Chawla answered |
The equation of the plane through the line of intersection of the planes
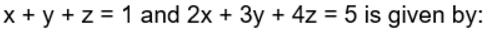
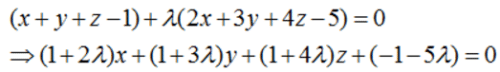
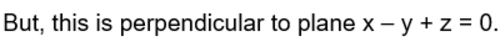
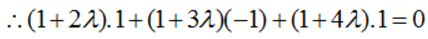
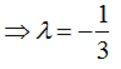
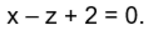
Direction: Read the following text and answer the following questions on the basis of the same:A cricket match is organized between two Clubs A and B for which a team from each club is chosen. Remaining players of Club A and Club B are respectively sitting on the plane represented by the equation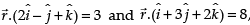 
to cheer the team of their own clubs.
Q. The distance of the plane, on which players of Club B are seated, from the origin is- a)
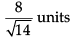
- b)
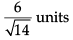
- c)
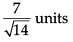
- d)
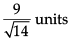
Correct answer is option 'A'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
A cricket match is organized between two Clubs A and B for which a team from each club is chosen. Remaining players of Club A and Club B are respectively sitting on the plane represented by the equation 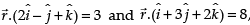to cheer the team of their own clubs.
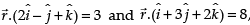to cheer the team of their own clubs.Q. The distance of the plane, on which players of Club B are seated, from the origin is
a)
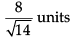
b)
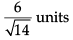
c)
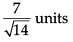
d)
|
|
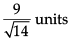
Geetika Shah answered |
We know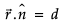
∴ 
∴ 
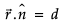
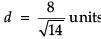
The angle between two lines whose direction ratios are 1,2,1 and 2,-3,4 is:- a)30°
- b)60°
- c)90°
- d)45°
Correct answer is option 'C'. Can you explain this answer?
The angle between two lines whose direction ratios are 1,2,1 and 2,-3,4 is:
a)
30°
b)
60°
c)
90°
d)
45°
|
O Kaif Sid answered |
Cosx =( i+2j+k).(2i-3j+4k)/ √1+4+1 × √4+9+16
cosx= 2-6+4/√1+4+1 × √4+9+16
cosx = 0/√1+4+1 × √4+9+16
cosx = 0
therfore
x = 90
cosx= 2-6+4/√1+4+1 × √4+9+16
cosx = 0/√1+4+1 × √4+9+16
cosx = 0
therfore
x = 90
Find the distance of the point (0, 0, 0) from the plane 3x – 4y + 12 z = 3- a)9/13
- b)7/13
- c)5/13
- d)3/13
Correct answer is option 'D'. Can you explain this answer?
Find the distance of the point (0, 0, 0) from the plane 3x – 4y + 12 z = 3
a)
9/13
b)
7/13
c)
5/13
d)
3/13
|
Krish Ghoshal answered |
As we know that the length of the perpendicular from point
P(x1,y1,z1) from the plane a1x+b1y+c1z+d1 = 0 is given by:
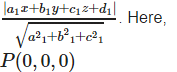
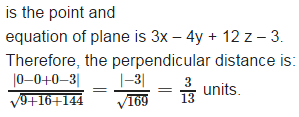
P(x1,y1,z1) from the plane a1x+b1y+c1z+d1 = 0 is given by:
Direction: Read the following text and answer the following questions on the basis of the same:The equation of motion of a missile are x = 3t, y = –4t, z = t, where the time ‘t’ is given in seconds, and the distance is measured in kilometres.
Q. At what distance will the rocket be from the starting point (0, 0, 0) in 5 seconds?- a)
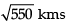
- b)
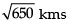
- c)
- d)
Correct answer is option 'B'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
The equation of motion of a missile are x = 3t, y = –4t, z = t, where the time ‘t’ is given in seconds, and the distance is measured in kilometres.
Q. At what distance will the rocket be from the starting point (0, 0, 0) in 5 seconds?
a)
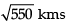
b)
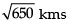
c)
d)
|
Cstoppers Instructors answered |
Here,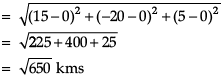
t = 5 seconds
x = 3t = 3 x 5 = 15
y = -4t = -4 x 5 = -20
z = t = 5
(x, y, z) (15, -20, 5)
Distance from starting point(0, 0, 0)
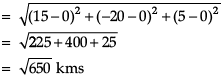
Direction: Read the following text and answer the following questions on the basis of the same:A cricket match is organized between two Clubs A and B for which a team from each club is chosen. Remaining players of Club A and Club B are respectively sitting on the plane represented by the equation 
to cheer the team of their own clubs.
Q. The Cartesian equation of the plane on which players of Club A are seated is- a)2x − y + z = 3
- b)2x − y + 2z = 3
- c)2x − y + z =−3
- d)x − t + z = 3
Correct answer is option 'A'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
A cricket match is organized between two Clubs A and B for which a team from each club is chosen. Remaining players of Club A and Club B are respectively sitting on the plane represented by the equation to cheer the team of their own clubs.
to cheer the team of their own clubs.Q. The Cartesian equation of the plane on which players of Club A are seated is
a)
2x − y + z = 3
b)
2x − y + 2z = 3
c)
2x − y + z =−3
d)
x − t + z = 3
|
|
Anjali Sharma answered |
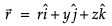
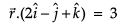
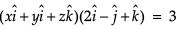
2x - y + z = 3
Three planes, viz the XY Plane, XZ Plane and the YZ Plane divide the space into eight parts. Each part is called an OCTANT. What is the relation between these three planes- a)They form the angles α, β & γ with each other
- b)Any two must be perpendicular to each other.
- c)All three are mutually perpendicular
- d)no relation between these three planes
Correct answer is option 'C'. Can you explain this answer?
Three planes, viz the XY Plane, XZ Plane and the YZ Plane divide the space into eight parts. Each part is called an OCTANT. What is the relation between these three planes
a)
They form the angles α, β & γ with each other
b)
Any two must be perpendicular to each other.
c)
All three are mutually perpendicular
d)
no relation between these three planes
|
|
Janani Pillai answered |
The three mutually perpendicular coordinate planes which in turn divide the space into eight parts and each part is known as octant.
The direction cosines of the line equally inclined with the axes, are:- a)1, 1, 1,
- b)0, 0, 0
- c)1/3, 1/3, 1/3
- d)1/√3, 1/√3, 1/√3
Correct answer is option 'D'. Can you explain this answer?
The direction cosines of the line equally inclined with the axes, are:
a)
1, 1, 1,
b)
0, 0, 0
c)
1/3, 1/3, 1/3
d)
1/√3, 1/√3, 1/√3
|
Geetika Mehta answered |
Direction cosines are the ratios of the direction ratios of a line. In other words, they represent the cosines of the angles that the line makes with the positive x, y, and z axes.
Let's consider a line equally inclined with the axes. This means that the line makes equal angles with each axis.
To find the direction cosines of this line, we need to determine the cosines of the angles it makes with the x, y, and z axes.
Let's assume that the line makes an angle of θ with each axis. Since the line is equally inclined with the axes, all the angles are equal.
Let's calculate the direction cosine along the x-axis:
cos(θ) = adjacent side / hypotenuse
cos(θ) = 1 / hypotenuse
hypotenuse = 1 / cos(θ)
Similarly, the direction cosine along the y-axis and z-axis would also be 1 / cos(θ).
Therefore, the direction cosines of the line equally inclined with the axes are (1 / cos(θ), 1 / cos(θ), 1 / cos(θ)).
Since the line is equally inclined with the axes, the angle θ is the same for all three direction cosines.
Hence, the correct answer is option D: 1/3, 1/3, 1/3.
Let's consider a line equally inclined with the axes. This means that the line makes equal angles with each axis.
To find the direction cosines of this line, we need to determine the cosines of the angles it makes with the x, y, and z axes.
Let's assume that the line makes an angle of θ with each axis. Since the line is equally inclined with the axes, all the angles are equal.
Let's calculate the direction cosine along the x-axis:
cos(θ) = adjacent side / hypotenuse
cos(θ) = 1 / hypotenuse
hypotenuse = 1 / cos(θ)
Similarly, the direction cosine along the y-axis and z-axis would also be 1 / cos(θ).
Therefore, the direction cosines of the line equally inclined with the axes are (1 / cos(θ), 1 / cos(θ), 1 / cos(θ)).
Since the line is equally inclined with the axes, the angle θ is the same for all three direction cosines.
Hence, the correct answer is option D: 1/3, 1/3, 1/3.
Direction: Read the following text and answer the following questions on the basis of the same:The Indian coast guard, while patrolling, saw a suspicious boat with people. They were nowhere looking like fishermen. The coast guard were closely observing the movement of the boat for an opportunity to seize the boat. They observed that the boat is moving along a planar surface. At an instant of time, the coordinates of the position of the coast guard helicopter and the boat is (1, 3, 5) and (2, 5, 3) respectively.
Q. At that given instant of time, the equation of line passing through the positions of the helicopter and boat is- a)
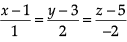
- b)
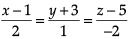
- c)
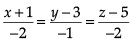
- d)
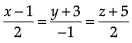
Correct answer is option 'A'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
The Indian coast guard, while patrolling, saw a suspicious boat with people. They were nowhere looking like fishermen. The coast guard were closely observing the movement of the boat for an opportunity to seize the boat. They observed that the boat is moving along a planar surface. At an instant of time, the coordinates of the position of the coast guard helicopter and the boat is (1, 3, 5) and (2, 5, 3) respectively.
Q. At that given instant of time, the equation of line passing through the positions of the helicopter and boat is
a)
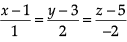
b)
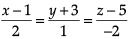
c)
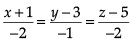
d)
|
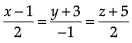
Top Rankers answered |
Here, direction cosines are 1, 2, –2.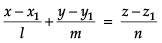
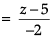
Equation of line passing through the positions of the helicopter and boat is
⇒ 
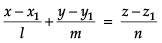
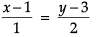
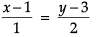
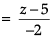
Equation of a plane which is at a distance d from the origin and the direction cosines of the normal to the plane are l, m, n is.- a)lx – my + nz = d
- b)– lx + my + nz = d
- c)lx + my + nz = d
- d)lx + my + nz = – d
Correct answer is option 'C'. Can you explain this answer?
Equation of a plane which is at a distance d from the origin and the direction cosines of the normal to the plane are l, m, n is.
a)
lx – my + nz = d
b)
– lx + my + nz = d
c)
lx + my + nz = d
d)
lx + my + nz = – d
|
Aravind Nambiar answered |
In Cartesian co – ordinate system Equation of a plane which is at a distance d from the origin and the direction cosines of the normal to the plane are l, m, n is given by : lx + my + nz = d.
Direction: Read the following text and answer the following questions on the basis of the same:Consider the plane π1 : 2x – 3y + 4z + 9 = 0 and the point P(1, –2, 3). π1 is a plane parallel to π1 and containing the point P.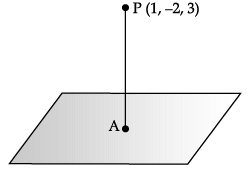
Q. Distance between π1 and π2 is _______ units.- a)5
- b)
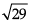
- c)
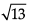
- d)2√3
Correct answer is option 'B'. Can you explain this answer?
Direction: Read the following text and answer the following questions on the basis of the same:
Consider the plane π1 : 2x – 3y + 4z + 9 = 0 and the point P(1, –2, 3). π1 is a plane parallel to π1 and containing the point P.
Q. Distance between π1 and π2 is _______ units.
a)
5
b)
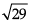
c)
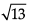
d)
2√3
|
|
Swati Verma answered |
Distance between π1 and π2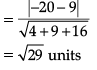
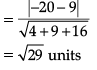
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice asAssertion (A): P is a point on the line segment joining the points (3, 2, –1) and (6, –4, –2). If x coordinate of P is 5, then its y coordinate is –2.Reason (R): The two lines x = ay + b, z = cy + d and x = a’y + b’, z = c’y + d’ will be perpendicular, iff aa’ + bb’ + cc’ = 0.- a)Both A and R are true and R is the correct explanation of A
- b)Both A and R are true but R is NOT the correct explanation of A
- c)A is true but R is false
- d)A is false but R is True
Correct answer is option 'C'. Can you explain this answer?
Direction: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as
Assertion (A): P is a point on the line segment joining the points (3, 2, –1) and (6, –4, –2). If x coordinate of P is 5, then its y coordinate is –2.
Reason (R): The two lines x = ay + b, z = cy + d and x = a’y + b’, z = c’y + d’ will be perpendicular, iff aa’ + bb’ + cc’ = 0.
a)
Both A and R are true and R is the correct explanation of A
b)
Both A and R are true but R is NOT the correct explanation of A
c)
A is true but R is false
d)
A is false but R is True
|
|
Shalini Bose answered |
Assertion (A): P is a point on the line segment joining the points (3, 2, –1) and (6, –4, –2). If x coordinate of P is 5, then its y coordinate is –2.
Reason (R): The two lines x = ay b, z = cy d and x = a’y b’, z = c’y d’ will be perpendicular, iff aa’ bb’ cc’ = 0.
The given assertion relates to the coordinates of a point P on a line segment joining two given points. The reason provided relates to the condition for two lines to be perpendicular.
Explanation:
To understand this assertion and reason, let's first find the equation of the line segment joining the points (3, 2, –1) and (6, –4, –2).
The equation of a line segment joining two points (x₁, y₁, z₁) and (x₂, y₂, z₂) can be written as:
(x - x₁)/(x₂ - x₁) = (y - y₁)/(y₂ - y₁) = (z - z₁)/(z₂ - z₁)
Plugging in the given values, we have:
(x - 3)/(6 - 3) = (y - 2)/(-4 - 2) = (z + 1)/(-2 - (-1))
Simplifying, we get:
(x - 3)/3 = (y - 2)/(-6) = (z + 1)/(-1)
Now, let's consider the x-coordinate of P as 5. Substituting this value into the equation, we get:
(5 - 3)/3 = (y - 2)/(-6) = (z + 1)/(-1)
2/3 = (y - 2)/(-6) = (z + 1)/(-1)
Simplifying further, we get:
(y - 2)/(-6) = (z + 1)/(-1)
Cross-multiplying, we get:
-6(y - 2) = -1(z + 1)
Expanding, we get:
-6y + 12 = -z - 1
Rearranging, we get:
z = -6y + 13
Comparing this equation with the given equations:
x = ay + b
z = cy + d
We can see that a = 0, b = 0, c = -6, and d = 13.
Now, let's consider the given reason. According to the reason, the two lines x = ay + b, z = cy + d and x = a'y + b', z = c'y + d' will be perpendicular if aa' + bb' + cc' = 0.
Plugging in the values, we have:
(0)(0) + (0)(0) + (-6)(0) = 0
Therefore, aa' + bb' + cc' = 0, which means the two lines are perpendicular.
Therefore, both the assertion and the reason are true, and the reason correctly explains the assertion.
Hence, the correct answer is option C.
Reason (R): The two lines x = ay b, z = cy d and x = a’y b’, z = c’y d’ will be perpendicular, iff aa’ bb’ cc’ = 0.
The given assertion relates to the coordinates of a point P on a line segment joining two given points. The reason provided relates to the condition for two lines to be perpendicular.
Explanation:
To understand this assertion and reason, let's first find the equation of the line segment joining the points (3, 2, –1) and (6, –4, –2).
The equation of a line segment joining two points (x₁, y₁, z₁) and (x₂, y₂, z₂) can be written as:
(x - x₁)/(x₂ - x₁) = (y - y₁)/(y₂ - y₁) = (z - z₁)/(z₂ - z₁)
Plugging in the given values, we have:
(x - 3)/(6 - 3) = (y - 2)/(-4 - 2) = (z + 1)/(-2 - (-1))
Simplifying, we get:
(x - 3)/3 = (y - 2)/(-6) = (z + 1)/(-1)
Now, let's consider the x-coordinate of P as 5. Substituting this value into the equation, we get:
(5 - 3)/3 = (y - 2)/(-6) = (z + 1)/(-1)
2/3 = (y - 2)/(-6) = (z + 1)/(-1)
Simplifying further, we get:
(y - 2)/(-6) = (z + 1)/(-1)
Cross-multiplying, we get:
-6(y - 2) = -1(z + 1)
Expanding, we get:
-6y + 12 = -z - 1
Rearranging, we get:
z = -6y + 13
Comparing this equation with the given equations:
x = ay + b
z = cy + d
We can see that a = 0, b = 0, c = -6, and d = 13.
Now, let's consider the given reason. According to the reason, the two lines x = ay + b, z = cy + d and x = a'y + b', z = c'y + d' will be perpendicular if aa' + bb' + cc' = 0.
Plugging in the values, we have:
(0)(0) + (0)(0) + (-6)(0) = 0
Therefore, aa' + bb' + cc' = 0, which means the two lines are perpendicular.
Therefore, both the assertion and the reason are true, and the reason correctly explains the assertion.
Hence, the correct answer is option C.
Chapter doubts & questions for Chapter 11 - Three Dimensional Geometry - Mathematics CUET UG Mock Test Series 2026 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Chapter 11 - Three Dimensional Geometry - Mathematics CUET UG Mock Test Series 2026 in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup