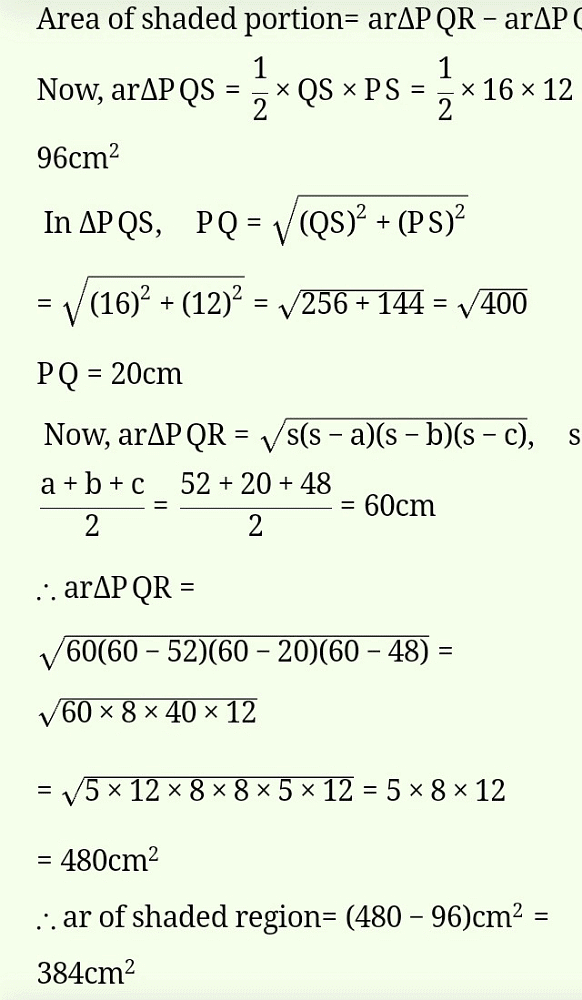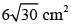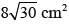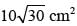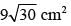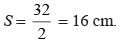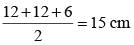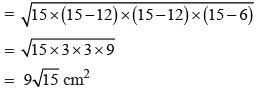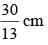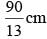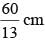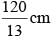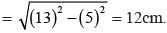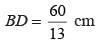All Exams >
Class 9 >
Mathematics Olympiad for Class 9 >
All Questions
All questions of Heron’s Formula for Class 9 Exam
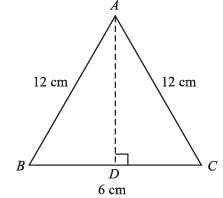
The area of an isosceles triangles whose equal sides are 12cm and the other side is 6cm long, will be :- a)3 √15 cm2
- b)6 √15 cm2
- c)9 √15 cm2
- d)12√15 cm2
Correct answer is option 'C'. Can you explain this answer?
The area of an isosceles triangles whose equal sides are 12cm and the other side is 6cm long, will be :
a)
3 √15 cm2
b)
6 √15 cm2
c)
9 √15 cm2
d)
12√15 cm2
|
Nilanjan Ghosh answered |
The area of an isosceles triangle can be found using the formula:
Area = (base * height) / 2
In this case, the base is the side that is 6cm long, and the height is the perpendicular distance from the base to the vertex of the triangle.
Since the triangle is isosceles, the height bisects the base and divides it into two equal parts.
Therefore, each part of the base is 6cm / 2 = 3cm.
Using the Pythagorean theorem, we can find the height:
(12cm)^2 = (3cm)^2 + height^2
144cm^2 = 9cm^2 + height^2
height^2 = 144cm^2 - 9cm^2
height^2 = 135cm^2
height = sqrt(135cm^2)
height = 11.61cm
Substituting the values into the formula:
Area = (6cm * 11.61cm) / 2 = 69.66cm^2
Therefore, the area of the isosceles triangle is approximately 69.66cm^2.
So the correct answer would be:
b) 69.66cm^2
Area = (base * height) / 2
In this case, the base is the side that is 6cm long, and the height is the perpendicular distance from the base to the vertex of the triangle.
Since the triangle is isosceles, the height bisects the base and divides it into two equal parts.
Therefore, each part of the base is 6cm / 2 = 3cm.
Using the Pythagorean theorem, we can find the height:
(12cm)^2 = (3cm)^2 + height^2
144cm^2 = 9cm^2 + height^2
height^2 = 144cm^2 - 9cm^2
height^2 = 135cm^2
height = sqrt(135cm^2)
height = 11.61cm
Substituting the values into the formula:
Area = (6cm * 11.61cm) / 2 = 69.66cm^2
Therefore, the area of the isosceles triangle is approximately 69.66cm^2.
So the correct answer would be:
b) 69.66cm^2
If the length of each side of a triangle is multiplied by 3, then the % increase in area will be:- a)400%
- b)800%
- c)700%
- d)900%
Correct answer is option 'B'. Can you explain this answer?
If the length of each side of a triangle is multiplied by 3, then the % increase in area will be:
a)
400%
b)
800%
c)
700%
d)
900%
|
Nirali Shah answered |
Understanding Area of a Triangle
The area of a triangle is given by the formula:
Area = 1/2 * base * height.
When the lengths of the sides of a triangle are multiplied by a factor, the area changes based on the square of that factor.
Effect of Scaling on Area
- If each side of the triangle is multiplied by 3, the new lengths become 3 times the original lengths.
- The new area can be calculated as:
New Area = 1/2 * (3 * base) * (3 * height) = 9 * (1/2 * base * height) = 9 * Original Area.
Calculating the Percentage Increase
- The increase in area can be determined as follows:
Increase in Area = New Area - Original Area = 9 * Original Area - Original Area = 8 * Original Area.
- To find the percentage increase, we use the formula:
Percentage Increase = (Increase in Area / Original Area) * 100.
- Substituting the values, we get:
Percentage Increase = (8 * Original Area / Original Area) * 100 = 800%.
Final Conclusion
Thus, when the length of each side of a triangle is multiplied by 3, the area increases by 800%. Therefore, the correct answer is option 'B'.
The area of a triangle is given by the formula:
Area = 1/2 * base * height.
When the lengths of the sides of a triangle are multiplied by a factor, the area changes based on the square of that factor.
Effect of Scaling on Area
- If each side of the triangle is multiplied by 3, the new lengths become 3 times the original lengths.
- The new area can be calculated as:
New Area = 1/2 * (3 * base) * (3 * height) = 9 * (1/2 * base * height) = 9 * Original Area.
Calculating the Percentage Increase
- The increase in area can be determined as follows:
Increase in Area = New Area - Original Area = 9 * Original Area - Original Area = 8 * Original Area.
- To find the percentage increase, we use the formula:
Percentage Increase = (Increase in Area / Original Area) * 100.
- Substituting the values, we get:
Percentage Increase = (8 * Original Area / Original Area) * 100 = 800%.
Final Conclusion
Thus, when the length of each side of a triangle is multiplied by 3, the area increases by 800%. Therefore, the correct answer is option 'B'.
The area of an equilateral triangle with side 2√3 cm is- a)5.196 cm²
- b)0.866 cm²
- c)3.496 cm²
- d)1.732 cm²
Correct answer is option 'A'. Can you explain this answer?
The area of an equilateral triangle with side 2√3 cm is
a)
5.196 cm²
b)
0.866 cm²
c)
3.496 cm²
d)
1.732 cm²
|
|
Swati Verma answered |
Given, the side of an equilateral triangle = 2√3 cm
We have to find the area of the equilateral triangle.
Area of an equilateral triangle = √3/4 (side)²
= √3/4 (2√3)²
= √3/4 (4 × 3)
= 3√3
Consider √3 = 1.732
= 3 × 1.732
= 5.196 cm²
Therefore, the area of an equilateral triangle is 5.196 cm²
We have to find the area of the equilateral triangle.
Area of an equilateral triangle = √3/4 (side)²
= √3/4 (2√3)²
= √3/4 (4 × 3)
= 3√3
Consider √3 = 1.732
= 3 × 1.732
= 5.196 cm²
Therefore, the area of an equilateral triangle is 5.196 cm²
If a square and rhombus have same perimeter, and area of square is S and area of rhombus is R, then- a)S > R
- b)R > S
- c)R = S
- d)data insufficient
Correct answer is option 'A'. Can you explain this answer?
If a square and rhombus have same perimeter, and area of square is S and area of rhombus is R, then
a)
S > R
b)
R > S
c)
R = S
d)
data insufficient
|
|
Shilpa Choudhury answered |
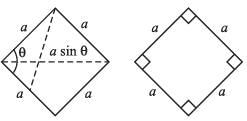
Area of square = a2
Area of rhombus = a2 sin θ
∵ sin θ < 1
∴ a2 > a2 sin θ
ar (square) > ar (rhombus)
⇒ S > R
The third side of triangle whose two sides are 26 and 28 cm and area is 336 cm2, is- a)29 cm
- b)27 cm
- c)30 cm
- d)32 cm
Correct answer is option 'C'. Can you explain this answer?
The third side of triangle whose two sides are 26 and 28 cm and area is 336 cm2, is
a)
29 cm
b)
27 cm
c)
30 cm
d)
32 cm
|
|
Shilpa Choudhury answered |
Let the length of third side be x.
∴
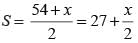
Area
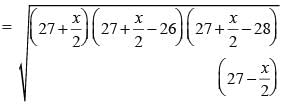
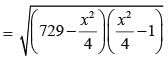
⇒ x = 30 cm.
∴ Third side = 30 cm.
∴
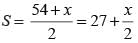
Area
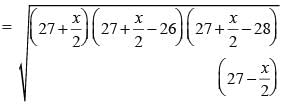
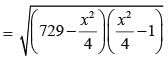
⇒ x = 30 cm.
∴ Third side = 30 cm.
The area of rhombus whose perimeter is 80m and one of the diagonal is 24m.- a)284m2
- b)384m2
- c)192m2
- d)374m2
Correct answer is option 'B'. Can you explain this answer?
The area of rhombus whose perimeter is 80m and one of the diagonal is 24m.
a)
284m2
b)
384m2
c)
192m2
d)
374m2
|
|
Shilpa Choudhury answered |
Side of rhombus =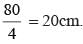 
∴ Length of other diagonal
∴
= 16 × 24 cm2 = 384 cm2
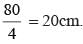
∴ Length of other diagonal
∴
= 16 × 24 cm2 = 384 cm2
Two parallel sides of a trapezium are 60cm and 77cm and other sides are 25cm and 26cm. The area of the trapezium is- a)622 cm2
- b)822 cm2
- c)1244 cm2
- d)1644 cm2
Correct answer is option 'D'. Can you explain this answer?
Two parallel sides of a trapezium are 60cm and 77cm and other sides are 25cm and 26cm. The area of the trapezium is
a)
622 cm2
b)
822 cm2
c)
1244 cm2
d)
1644 cm2
|
|
Shilpa Choudhury answered |
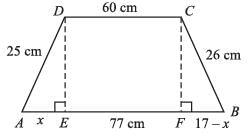AE = x, FB = (17 – x) cm.From ∆AED, and ∆CFB
CF2 = DE2
⇒ (26)2 – (17 – x)2 = (25)2 – (x)2
⇒ (26)2 – (25)2 = (17 – x)2 – (x)2
⇒ (26 – 25) (26 + 25) = (17 – x + x) (17 – x – x)
⇒ 51 = 17 (17 – 2x)
⇒ 17 – 2x = 3
⇒ 2x = 14 ⇒ x = 7cm.
∴ area = 
= 137 × 12 cm2 = 1644 cm2
The sides of a triangle are 50 cm, 78 cm and 112 cm. the smallest altitude is:- a)50 cm
- b)40 cm
- c)30 cm
- d)25 cm
Correct answer is option 'C'. Can you explain this answer?
The sides of a triangle are 50 cm, 78 cm and 112 cm. the smallest altitude is:
a)
50 cm
b)
40 cm
c)
30 cm
d)
25 cm
|
|
Shilpa Choudhury answered |
Here S =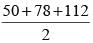 
= 120cm.
∴Area
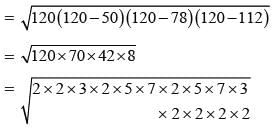
= 2 × 3 × 2 × 2 × 2 × 5 × 7
= 240 × 7 cm2 = 1680 cm2
Area = 1/2 x base altitude = 1680 cm2
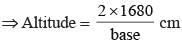
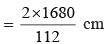
= 30 cm
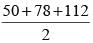= 120cm.∴Area
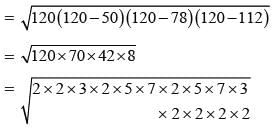
= 2 × 3 × 2 × 2 × 2 × 5 × 7
= 240 × 7 cm2 = 1680 cm2
Area = 1/2 x base altitude = 1680 cm2
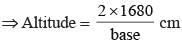
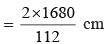
= 30 cm
A square and an equilateral triangle have equal perimeters. If the diagonal of the square is 12√2 cm, the area of the triangle is : - a)24√2 cm2
- b)48√3 cm2
- c)24√3 cm2
- d)64√3 c m2
Correct answer is option 'D'. Can you explain this answer?
A square and an equilateral triangle have equal perimeters. If the diagonal of the square is 12√2 cm, the area of the triangle is :
a)
24√2 cm2
b)
48√3 cm2
c)
24√3 cm2
d)
64√3 c m2
|
|
Shilpa Choudhury answered |
Length of equilateral triangle = x/3 cm
Length of side of square = x/4 cm
Length of side of square
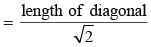
= 12 cm.
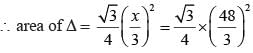
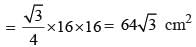
Length of side of square = x/4 cm
Length of side of square
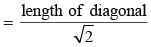
= 12 cm.
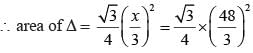
ABCD is a parallelogram, where,
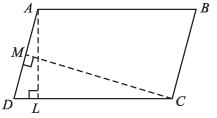AL = 8 cm, CM = 10 cm, AD = 6 cm. find AB.- a)6.5 cm
- b)6 cm
- c)7 cm
- d)7.5 cm
Correct answer is option 'D'. Can you explain this answer?
ABCD is a parallelogram, where,
AL = 8 cm, CM = 10 cm, AD = 6 cm. find AB.
a)
6.5 cm
b)
6 cm
c)
7 cm
d)
7.5 cm
|
|
Shilpa Choudhury answered |
Area of ∥gm = AL × DC = CM × AD
⇒ 8 × DC = 10 × 6
⇒
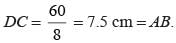
⇒ 8 × DC = 10 × 6
⇒
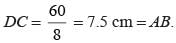
The length of sides of a triangle are in the ratio 3 : 4 : 5 and its perimeter is 144 cm, then, the height corresponding to the length side is: - a)27.8 cm
- b)26.8 cm
- c)28.8 cm
- d)30.8 cm
Correct answer is option 'C'. Can you explain this answer?
The length of sides of a triangle are in the ratio 3 : 4 : 5 and its perimeter is 144 cm, then, the height corresponding to the length side is:
a)
27.8 cm
b)
26.8 cm
c)
28.8 cm
d)
30.8 cm
|
|
Shilpa Choudhury answered |
Lengths of sides of triangle
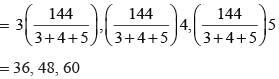∴ Area
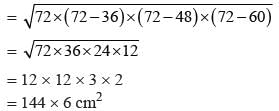
∴ Height corresponding to the longest side
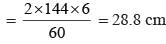
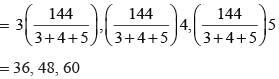∴ Area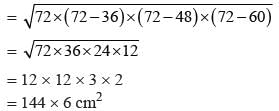∴ Height corresponding to the longest side
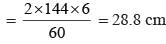
The sides of a triangle are 11cm, 15cm and 16 cm. The altitude to the largest side is: - a)30 cm
- b)
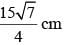
- c)
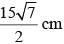
- d)20 √7 cm
Correct answer is option 'B'. Can you explain this answer?
The sides of a triangle are 11cm, 15cm and 16 cm. The altitude to the largest side is:
a)
30 cm
b)
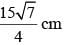
c)
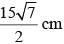
d)
20 √7 cm
|
|
Shilpa Choudhury answered |
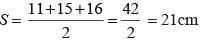
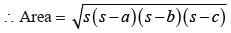
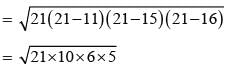
= 5 × 2 × 3√7
= √cm2
1/2 × Altitude to the largest side × largest side = 30√7 cm2
⇒ Altitude to the largest side
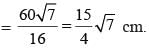
Area of the figure is :
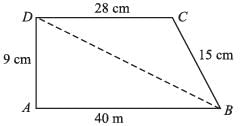
- a)216 m2
- b)316 m2
- c)306 m2
- d)206 m2
Correct answer is option 'C'. Can you explain this answer?
Area of the figure is :
a)
216 m2
b)
316 m2
c)
306 m2
d)
206 m2
|
|
Shilpa Choudhury answered |
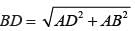
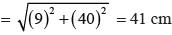
∴ For ∆DBC,
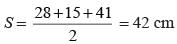
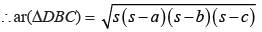
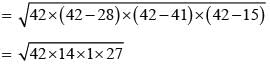
= 14 × 3 × 3
= 126 cm2
Ar(∆ABD) = 1/2 x 9 x 40
= 180 cm2
∴ Total area = (126 + 180) cm2
= 306 cm2
The length of median of an equilateral triangle is √3 cm. The area of triangle is. - a)2√3 cm2
- b)4√3 cm2
- c)√3 cm2
- d)3√3 cm2
Correct answer is option 'C'. Can you explain this answer?
The length of median of an equilateral triangle is √3 cm. The area of triangle is.
a)
2√3 cm2
b)
4√3 cm2
c)
√3 cm2
d)
3√3 cm2
|
|
Shilpa Choudhury answered |
Length of median of equilateral triangle
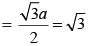
⇒ a = 2 cm.
∴ Area of triangle
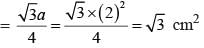
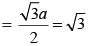
⇒ a = 2 cm.
∴ Area of triangle
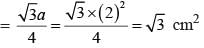
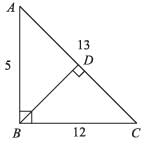
Find the length BD, from the previous question:- a)120 cm
- b)60 cm
- c)80 cm
- d)160 cm
Correct answer is option 'A'. Can you explain this answer?
Find the length BD, from the previous question:
a)
120 cm
b)
60 cm
c)
80 cm
d)
160 cm
|
|
Shilpa Choudhury answered |
BD = 2 × OD = 2 × 60 = 120 cm
The diagonal of a parallelogram divide it in 2 parts, the area of the two parts: - a)will be equal
- b)will be unequal
- c)cannot be compared
- d)2/3 of the area of parallelogram
Correct answer is option 'A'. Can you explain this answer?
The diagonal of a parallelogram divide it in 2 parts, the area of the two parts:
a)
will be equal
b)
will be unequal
c)
cannot be compared
d)
2/3 of the area of parallelogram
|
|
Shilpa Choudhury answered |
The two parts of ∥gm are congruent.
∴ they have equal area.
∴ they have equal area.
If a square and equilateral triangle have same perimeter and, square has area A1 and equilateral triangle has area A2, then. - a)A1 = A2
- b)A1 > A2
- c)A2 > A1
- d)
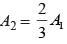
Correct answer is option 'B'. Can you explain this answer?
If a square and equilateral triangle have same perimeter and, square has area A1 and equilateral triangle has area A2, then.
a)
A1 = A2
b)
A1 > A2
c)
A2 > A1
d)
|
|
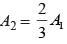
Shilpa Choudhury answered |
Perimeter of square = Perimeter of equilateral ∆ = x.
∴ length of side of square = x/4
Length of side of equilateral ∆ = x/3
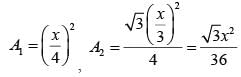Clearly, A1 > A2
∴ length of side of square = x/4
Length of side of equilateral ∆ = x/3
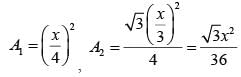Clearly, A1 > A2If each side of ∆ is doubled, then the area will become how many times? - a)2 times
- b)3 times
- c)4 times
- d)8 times
Correct answer is option 'C'. Can you explain this answer?
If each side of ∆ is doubled, then the area will become how many times?
a)
2 times
b)
3 times
c)
4 times
d)
8 times
|
|
Shilpa Choudhury answered |
If the sides of ∆ are a, b and c.
∴ New sides are 2a, 2b, 2c.
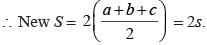
∴ New area =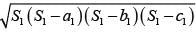
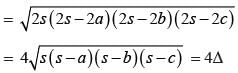
∴ New sides are 2a, 2b, 2c.
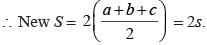
∴ New area =
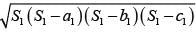
Area of parallelogram, in the adjoining figure will be :
- a)336 cm2
- b)672 cm2
- c)1008 cm2
- d)1080 cm2
Correct answer is option 'B'. Can you explain this answer?
Area of parallelogram, in the adjoining figure will be :
a)
336 cm2
b)
672 cm2
c)
1008 cm2
d)
1080 cm2
|
|
Shilpa Choudhury answered |
Area of ∆ACD = area of ∆ACB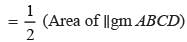
⇒ area of ∆ACD =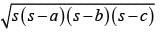
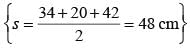
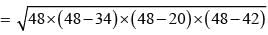
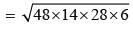
= 4 × 6 × 7 × 2
= 4 × 84 = 336 cm2
∴ area of ∥gm = 2 × ar(∆ACD)
= 2 × 336 cm2
= 672 cm2
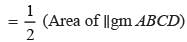
⇒ area of ∆ACD =
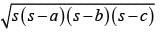
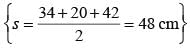
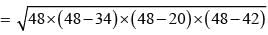
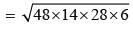
= 4 × 6 × 7 × 2
= 4 × 84 = 336 cm2
∴ area of ∥gm = 2 × ar(∆ACD)
= 2 × 336 cm2
= 672 cm2
Find the area of the given figure :
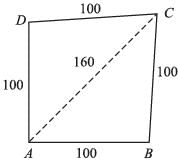
- a)4800 cm2
- b)5600 cm2
- c)9600 cm2
- d)8800 cm2
Correct answer is option 'C'. Can you explain this answer?
Find the area of the given figure :
a)
4800 cm2
b)
5600 cm2
c)
9600 cm2
d)
8800 cm2
|
|
Shilpa Choudhury answered |
In ∆DOC,
OD2 + OC2 = DC2
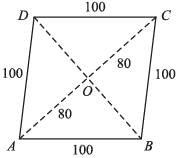
⇒ OD =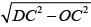
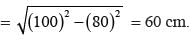
∴ DB = 2 × OD = 2 × 60 = 120 cm.
Area of rhombus =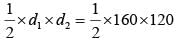
= 9600 cm2
OD2 + OC2 = DC2
⇒ OD =
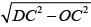
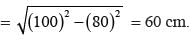
∴ DB = 2 × OD = 2 × 60 = 120 cm.
Area of rhombus =
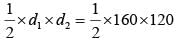
= 9600 cm2
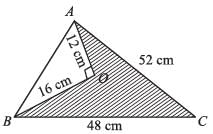
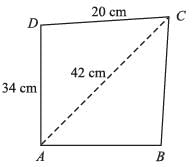
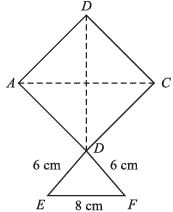
The area of kite in the adjoining figure is : (AC = BD = 32 cm)
- a)512 cm2
- b)529.84 cm2
- c)512.84 cm2
- d)517.84 cm2
Correct answer is option 'B'. Can you explain this answer?
The area of kite in the adjoining figure is : (AC = BD = 32 cm)
a)
512 cm2
b)
529.84 cm2
c)
512.84 cm2
d)
517.84 cm2
|
|
Shilpa Choudhury answered |
Area of square ABCD = 1/2 × AC × BD
= 1/2 x 32 x 32
= 16 × 32 cm2
= 512 cm2
Here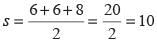
= 1/2 x 32 x 32
= 16 × 32 cm2
= 512 cm2
Here
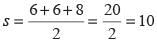
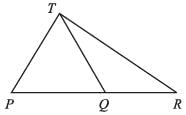
In the figure, PQ : QR = 3 : 2. If the area of ∆PRT = 40 cm2, then area of ∆TQR is:
- a)15cm2
- b)16cm2
- c)35cm2
- d)30cm2
Correct answer is option 'B'. Can you explain this answer?
In the figure, PQ : QR = 3 : 2. If the area of ∆PRT = 40 cm2, then area of ∆TQR is:
a)
15cm2
b)
16cm2
c)
35cm2
d)
30cm2
|
|
Shilpa Choudhury answered |
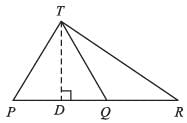
⇒ ar (∆PQT) = 24 cm2
∴ area (∆TQR) = ar (∆PRT) – ar (∆PQT) = 40 – 24 = 16cm2
Chapter doubts & questions for Heron’s Formula - Mathematics Olympiad for Class 9 2025 is part of Class 9 exam preparation. The chapters have been prepared according to the Class 9 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 9 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Heron’s Formula - Mathematics Olympiad for Class 9 in English & Hindi are available as part of Class 9 exam.
Download more important topics, notes, lectures and mock test series for Class 9 Exam by signing up for free.
Mathematics Olympiad for Class 9
23 videos|105 docs|45 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup