All Exams >
Class 1 >
Mental Maths >
All Questions
All questions of Shapes for Class 1 Exam
How is the total number of rectangles in a complex figure typically calculated?- a)By counting each edge
- b)By adding up the base numbers of smaller rectangles
- c)By measuring the perimeter
- d)By dividing the area by the number of edges
Correct answer is option 'B'. Can you explain this answer?
How is the total number of rectangles in a complex figure typically calculated?
a)
By counting each edge
b)
By adding up the base numbers of smaller rectangles
c)
By measuring the perimeter
d)
By dividing the area by the number of edges
|
|
Harsh mehra answered |
Total Number of Rectangles in a Complex Figure
Calculating the total number of rectangles in a complex figure involves understanding how rectangles can be formed by combining smaller rectangles or grid sections within the figure. Here's a detailed explanation:
Understanding Rectangles in a Figure
- Rectangles are defined by their width and height.
- In a complex figure, these dimensions can often be derived from smaller rectangles that make up the overall shape.
Counting Method
- Identify Smaller Rectangles: Break down the complex figure into recognizable smaller rectangles.
- Base Numbers: Each smaller rectangle contributes to the total count. For example, if a figure includes 3 smaller rectangles, you start with a base count of 3.
Adding Up
- Combining Counts: Once you have the base count of smaller rectangles, you can add these counts together.
- Overlap Consideration: Ensure that overlapping rectangles are not double-counted, as they should only be considered once in the total.
Conclusion
- By adding up the base numbers of smaller rectangles, you can effectively determine the total number of rectangles in the complex figure.
- This method not only simplifies the counting process but also ensures accuracy by focusing on distinct rectangles rather than edges or perimeter measurements.
This systematic approach allows for a clear and organized calculation of rectangles within any complex figure, making option 'B' the correct answer in determining the total number of rectangles.
Calculating the total number of rectangles in a complex figure involves understanding how rectangles can be formed by combining smaller rectangles or grid sections within the figure. Here's a detailed explanation:
Understanding Rectangles in a Figure
- Rectangles are defined by their width and height.
- In a complex figure, these dimensions can often be derived from smaller rectangles that make up the overall shape.
Counting Method
- Identify Smaller Rectangles: Break down the complex figure into recognizable smaller rectangles.
- Base Numbers: Each smaller rectangle contributes to the total count. For example, if a figure includes 3 smaller rectangles, you start with a base count of 3.
Adding Up
- Combining Counts: Once you have the base count of smaller rectangles, you can add these counts together.
- Overlap Consideration: Ensure that overlapping rectangles are not double-counted, as they should only be considered once in the total.
Conclusion
- By adding up the base numbers of smaller rectangles, you can effectively determine the total number of rectangles in the complex figure.
- This method not only simplifies the counting process but also ensures accuracy by focusing on distinct rectangles rather than edges or perimeter measurements.
This systematic approach allows for a clear and organized calculation of rectangles within any complex figure, making option 'B' the correct answer in determining the total number of rectangles.
What is a pattern of shapes?- a)A single shape repeated
- b)Random arrangement of shapes
- c)An arrangement of shapes in a specific order
- d)Shapes without any specific order
Correct answer is option 'C'. Can you explain this answer?
What is a pattern of shapes?
a)
A single shape repeated
b)
Random arrangement of shapes
c)
An arrangement of shapes in a specific order
d)
Shapes without any specific order

|
Keystone Instructors answered |
Patterns involve arranging shapes in a specific, often repeating order.
What is a polygon?- a)A shape with no sides
- b)A closed figure with three or more straight sides
- c)A shape with only curved lines
- d)A figure with exactly four sides
Correct answer is option 'B'. Can you explain this answer?
What is a polygon?
a)
A shape with no sides
b)
A closed figure with three or more straight sides
c)
A shape with only curved lines
d)
A figure with exactly four sides

|
Keystone Instructors answered |
A polygon is a closed figure with three or more straight sides.

Which shape can be described as having no corners and all points on the boundary equidistant from the center?- a)Square
- b)Oval
- c)Triangle
- d)Circle
Correct answer is option 'D'. Can you explain this answer?
Which shape can be described as having no corners and all points on the boundary equidistant from the center?
a)
Square
b)
Oval
c)
Triangle
d)
Circle
|
|
Harsh mehra answered |
Circle
Circle is the shape that can be described as having no corners and all points on the boundary equidistant from the center. Let's break down why a circle fits this description:
No Corners:
- Unlike a square, triangle, or oval, a circle does not have any corners or angles. It has a continuous curved boundary that smoothly connects all points on the perimeter.
All Points Equidistant:
- In a circle, every point on the boundary is the same distance away from the center. This property is what makes a circle a unique shape with perfect symmetry.
Properties of a Circle:
- A circle is defined as the set of all points in a plane that are a certain distance (radius) away from a fixed point (center).
- The distance from the center to any point on the boundary is always the same, making it a shape with radial symmetry.
Conclusion:
- In conclusion, a circle is the only shape that meets the criteria of having no corners and all points on the boundary equidistant from the center. Its unique properties make it a fundamental shape in geometry and mathematics.
Circle is the shape that can be described as having no corners and all points on the boundary equidistant from the center. Let's break down why a circle fits this description:
No Corners:
- Unlike a square, triangle, or oval, a circle does not have any corners or angles. It has a continuous curved boundary that smoothly connects all points on the perimeter.
All Points Equidistant:
- In a circle, every point on the boundary is the same distance away from the center. This property is what makes a circle a unique shape with perfect symmetry.
Properties of a Circle:
- A circle is defined as the set of all points in a plane that are a certain distance (radius) away from a fixed point (center).
- The distance from the center to any point on the boundary is always the same, making it a shape with radial symmetry.
Conclusion:
- In conclusion, a circle is the only shape that meets the criteria of having no corners and all points on the boundary equidistant from the center. Its unique properties make it a fundamental shape in geometry and mathematics.
What are edges in a shape?- a)The points where two sides meet.
- b)The lines that outline the shape.
- c)The angles between the sides.
- d)The center of the shape.
Correct answer is option 'B'. Can you explain this answer?
What are edges in a shape?
a)
The points where two sides meet.
b)
The lines that outline the shape.
c)
The angles between the sides.
d)
The center of the shape.

|
Keystone Instructors answered |
Edges are the lines or boundaries that define the shape.
Which shape has opposite sides equal and four right angles?- a)Circle
- b)Triangle
- c)Rectangle
- d)Oval
Correct answer is option 'C'. Can you explain this answer?
Which shape has opposite sides equal and four right angles?
a)
Circle
b)
Triangle
c)
Rectangle
d)
Oval

|
Keystone Instructors answered |
A rectangle has opposite sides that are equal and four right angles.


What characteristic is unique to a circle?

- a)It has three sides.
- b)It is perfectly round with no corners or edges.
- c)It has equal angles.
- d)It has a combination of straight and curved lines.
Correct answer is option 'B'. Can you explain this answer?
What characteristic is unique to a circle?


a)
It has three sides.
b)
It is perfectly round with no corners or edges.
c)
It has equal angles.
d)
It has a combination of straight and curved lines.

|
Keystone Instructors answered |
A circle is defined by having a perfectly round shape and no corners.
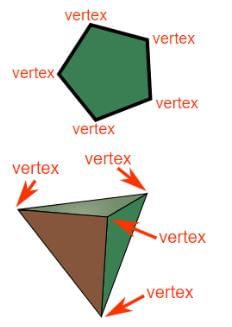
What are corners in geometric shapes also called?- a)Edges
- b)Faces
- c)Vertices
- d)Bases
Correct answer is option 'C'. Can you explain this answer?
What are corners in geometric shapes also called?
a)
Edges
b)
Faces
c)
Vertices
d)
Bases

|
Keystone Instructors answered |
Corners or vertices are where two or more edges meet.

If a shape has three sides of different lengths, what type of triangle is it?- a)Equilateral triangle
- b)Isosceles triangle
- c)Scalene triangle
- d)Right triangle
Correct answer is option 'C'. Can you explain this answer?
If a shape has three sides of different lengths, what type of triangle is it?
a)
Equilateral triangle
b)
Isosceles triangle
c)
Scalene triangle
d)
Right triangle

|
Keystone Instructors answered |
A scalene triangle has three sides of different lengths.

What is the correct term for the part of a shape where two sides meet?- a)Edge
- b)Vertex
- c)Face
- d)Base
Correct answer is option 'B'. Can you explain this answer?
What is the correct term for the part of a shape where two sides meet?
a)
Edge
b)
Vertex
c)
Face
d)
Base

|
Keystone Instructors answered |
A vertex is the point where two sides of a shape meet.

Which of the following is a property of a square?

- a)It has three equal sides.
- b)All sides are different in length.
- c)It has four equal sides and four right angles.
- d)It has curved sides.
Correct answer is option 'C'. Can you explain this answer?
Which of the following is a property of a square?


a)
It has three equal sides.
b)
All sides are different in length.
c)
It has four equal sides and four right angles.
d)
It has curved sides.

|
Keystone Instructors answered |
A square has four sides of equal length and four right angles.
Which shape has all its sides of equal length but does not necessarily have all angles equal?- a)Square
- b)Rectangle
- c)Parallelogram
- d)Rhombus
Correct answer is option 'D'. Can you explain this answer?
Which shape has all its sides of equal length but does not necessarily have all angles equal?
a)
Square
b)
Rectangle
c)
Parallelogram
d)
Rhombus

|
Keystone Instructors answered |
A rhombus has all sides of equal length, but its angles are not necessarily equal, unlike a square where all angles are 90 degrees.


In the concept of counting shapes, what is typically the first step?- a)Counting the edges
- b)Recognizing the shapes present
- c)Adding the areas of shapes
- d)Measuring the perimeter
Correct answer is option 'B'. Can you explain this answer?
In the concept of counting shapes, what is typically the first step?
a)
Counting the edges
b)
Recognizing the shapes present
c)
Adding the areas of shapes
d)
Measuring the perimeter

|
Keystone Instructors answered |
The first step is identifying the different shapes present in the figure.
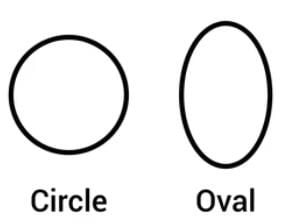
How can you distinguish an oval from a circle?- a)An oval has corners.
- b)A circle is longer than it is wide.
- c)An oval is symmetrical in all directions.
- d)An oval is stretched in one direction, unlike a circle.
Correct answer is option 'D'. Can you explain this answer?
How can you distinguish an oval from a circle?
a)
An oval has corners.
b)
A circle is longer than it is wide.
c)
An oval is symmetrical in all directions.
d)
An oval is stretched in one direction, unlike a circle.

|
Keystone Instructors answered |
An oval is an elongated circle, stretched in one direction, whereas a circle is perfectly round and symmetrical in all directions.

What shape is commonly used to represent a pizza slice?- a)Rectangle
- b)Square
- c)Circle
- d)Triangle
Correct answer is option 'D'. Can you explain this answer?
What shape is commonly used to represent a pizza slice?
a)
Rectangle
b)
Square
c)
Circle
d)
Triangle

|
Keystone Instructors answered |
A pizza slice is typically triangular in shape, resembling a triangle.


How many right angles does a rectangle have?
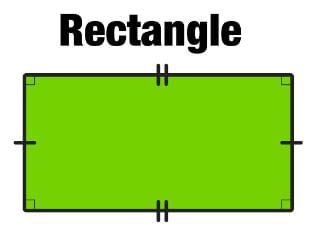
- a)2
- b)3
- c)5
- d)4
Correct answer is option 'D'. Can you explain this answer?
How many right angles does a rectangle have?


a)
2
b)
3
c)
5
d)
4

|
Keystone Instructors answered |
A rectangle has four right angles.
Which of the following is a closed shape?- a)C
- b)D
- c)S
- d)L
Correct answer is option 'B'. Can you explain this answer?
Which of the following is a closed shape?
a)
C
b)
D
c)
S
d)
L

|
Keystone Instructors answered |
The letter 'D' forms a closed loop, while 'C,' 'S,' and 'L' do not.
A triangle has:

- a)Three sides and three angles.
- b)Four sides and four angles.
- c)Two sides and two angles.
- d)No sides or angles.
Correct answer is option 'A'. Can you explain this answer?
A triangle has:


a)
Three sides and three angles.
b)
Four sides and four angles.
c)
Two sides and two angles.
d)
No sides or angles.

|
Keystone Instructors answered |
A triangle is a polygon with three sides and three angles.
Chapter doubts & questions for Shapes - Mental Maths 2025 is part of Class 1 exam preparation. The chapters have been prepared according to the Class 1 exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Class 1 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Shapes - Mental Maths in English & Hindi are available as part of Class 1 exam.
Download more important topics, notes, lectures and mock test series for Class 1 Exam by signing up for free.
Mental Maths
39 videos|158 docs|19 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily