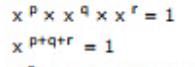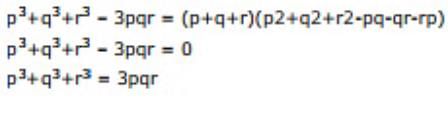All questions of Number System for Computer Science Engineering (CSE) Exam
In the examination a candidate must get 2/5 marks to pass, out of total marks.Shiyam appeared in the exam ang got 198 marks and still failed by 36 marks.The maximum mark is
- a)560
- b)610
- c)585
- d)480
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
In the examination a candidate must get 2/5 marks to pass, out of total marks.Shiyam appeared in the exam ang got 198 marks and still failed by 36 marks.The maximum mark is
a)
560
b)
610
c)
585
d)
480
e)
None of these

|
Quantronics answered |
2x = 198+36 = 234
Max = 234*5/2 = 585
Max = 234*5/2 = 585
In a three digit number the digit in the unit’s place is twice the digit in the ten’s place and 1.5 times the digit in the hundred’s place. If the sum of all the three digits of the number is 13, what is the number?- a)356
- b)456
- c)436
- d)626
- e)516
Correct answer is option 'C'. Can you explain this answer?
In a three digit number the digit in the unit’s place is twice the digit in the ten’s place and 1.5 times the digit in the hundred’s place. If the sum of all the three digits of the number is 13, what is the number?
a)
356
b)
456
c)
436
d)
626
e)
516

|
Bank Exams India answered |
100a + 10b + c
c = 2b → b = c/2
c = 1.5a → a = c/1.5
c/1.5 + c/2 + c = 13
6.5c = 39
c = 6, b = 3, a = 4 ⇒ 436
c = 2b → b = c/2
c = 1.5a → a = c/1.5
c/1.5 + c/2 + c = 13
6.5c = 39
c = 6, b = 3, a = 4 ⇒ 436
Sum of three consecutive odd numbers & three consecutive even numbers together is 231. Difference between the smallest odd number and the smallest even number is 11. What is the sum of the largest even number and largest odd number?- a)71
- b)91
- c)101
- d)81
- e)Can not be determined
Correct answer is option 'D'. Can you explain this answer?
Sum of three consecutive odd numbers & three consecutive even numbers together is 231. Difference between the smallest odd number and the smallest even number is 11. What is the sum of the largest even number and largest odd number?
a)
71
b)
91
c)
101
d)
81
e)
Can not be determined
|
|
Kendrika answered |
Let the three odd numbers be x, (x + 2), (x + 4) and
The three even numbers be (x + 11), (x + 13) and (x + 15)
Then,
⇔ x + (x + 2) + (x + 4) + (x + 11) + (x + 13) + (x + 15) = 231
⇔ 6x + 45 = 231
⇔ 6x = 186
⇔ x = 31
∴ Required sum :
= (x + 4) + (x + 15)
= 2x + 19
= 2 × 31 + 19
= 62 + 19
= 81
The three even numbers be (x + 11), (x + 13) and (x + 15)
Then,
⇔ x + (x + 2) + (x + 4) + (x + 11) + (x + 13) + (x + 15) = 231
⇔ 6x + 45 = 231
⇔ 6x = 186
⇔ x = 31
∴ Required sum :
= (x + 4) + (x + 15)
= 2x + 19
= 2 × 31 + 19
= 62 + 19
= 81
A number when divided by 143 leaves 31 as remainder. What will be the remainder
when the same number is divided by 13 ?- a)0
- b)1
- c)3
- d)5
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
A number when divided by 143 leaves 31 as remainder. What will be the remainder
when the same number is divided by 13 ?
when the same number is divided by 13 ?
a)
0
b)
1
c)
3
d)
5
e)
None of these

|
Abhishek answered |
Number is = x
x = divisor + remainder
x = 143 + 31
x = 174
when the same number is decided by 13
remainder= 174÷13
= 5 Ans.
x = divisor + remainder
x = 143 + 31
x = 174
when the same number is decided by 13
remainder= 174÷13
= 5 Ans.
The sum of two even numbers is six more than twice of the smaller number. If the difference between these two numbers is 6, If the larger number lies between 15 to 25 Which is the smaller number?
- a)16
- b)6
- c)24
- d)12
- e)Can not be determined
Correct answer is option 'D'. Can you explain this answer?
The sum of two even numbers is six more than twice of the smaller number. If the difference between these two numbers is 6, If the larger number lies between 15 to 25 Which is the smaller number?
a)
16
b)
6
c)
24
d)
12
e)
Can not be determined
|
|
Kavya Saxena answered |
If 12 is smaller number then larger number is 18
Sum = (12+18) = 30
Twice of the smaller number = 24.
The sum of two even numbers is six more than twice of the smaller number.
Therefore Number 12 satisfy both the conditions.
Sum = (12+18) = 30
Twice of the smaller number = 24.
The sum of two even numbers is six more than twice of the smaller number.
Therefore Number 12 satisfy both the conditions.
There are some Parrots and Some Lions in a forest.If the total number of animals head in forest are 840 and total no of animal legs are 1760.What is the number of Parots in the forest ?- a)800
- b)740
- c)620
- d)590
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
There are some Parrots and Some Lions in a forest.If the total number of animals head in forest are 840 and total no of animal legs are 1760.What is the number of Parots in the forest ?
a)
800
b)
740
c)
620
d)
590
e)
None of these

|
Naroj Boda answered |
2x+4(840-x) = 1760
2x+3360-4x = 1760
-2x = 1600
X = 1600/2 = 800
2x+3360-4x = 1760
-2x = 1600
X = 1600/2 = 800
If 4 is added to the numerator of a fraction it becomes 1/3 and if 3 is added to the denominator it becomes 1/6 then find the difference between numerator and denominator is- a)20
- b)21
- c)22
- d)24
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
If 4 is added to the numerator of a fraction it becomes 1/3 and if 3 is added to the denominator it becomes 1/6 then find the difference between numerator and denominator is
a)
20
b)
21
c)
22
d)
24
e)
None of these
|
|
Aisha Gupta answered |
(a +4)/b = 1/3 and a/(b+3) = 1/6 solve both the equations, u will get a = 5 and b = 27
A certain number of two digits is three times the sum of its digits. If 45 is added to it, the digits are reversed. The number is _______
- a)16
- b)72
- c)63
- d)27
- e)Can not be determined
Correct answer is option 'D'. Can you explain this answer?
A certain number of two digits is three times the sum of its digits. If 45 is added to it, the digits are reversed. The number is _______
a)
16
b)
72
c)
63
d)
27
e)
Can not be determined

|
KS Coaching Center answered |
A certain number of two digits is three times the sum of its digits only 27 satisfies this condition.
27 + 45 = 72
Therefore Ans is – 27
27 + 45 = 72
Therefore Ans is – 27
The sum of digits of a two digit number is 6. The ratio of the original number to the number formed by interchanging its digits is 4 : 7. Find the number.- a)60
- b)15
- c)42
- d)33
- e)24
Correct answer is option 'E'. Can you explain this answer?
The sum of digits of a two digit number is 6. The ratio of the original number to the number formed by interchanging its digits is 4 : 7. Find the number.
a)
60
b)
15
c)
42
d)
33
e)
24

|
Target Study Academy answered |
Let the number is 10x+y
So x+y = 6
And (10x+y)/(10y+x) = 4/7
Solve, 2x = y and from above we have x+y = 6
Solve both equations, x = 2, y = 4
So x+y = 6
And (10x+y)/(10y+x) = 4/7
Solve, 2x = y and from above we have x+y = 6
Solve both equations, x = 2, y = 4
When a number is added to 20 percent of the second number, we get 150 percent of the second number. Find the ratio between the first and second number?- a)13:9
- b)12:10
- c)13:10
- d)17:10
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
When a number is added to 20 percent of the second number, we get 150 percent of the second number. Find the ratio between the first and second number?
a)
13:9
b)
12:10
c)
13:10
d)
17:10
e)
None of these

|
Bank Exams India answered |
a + (20/100)*b = (150/100)*b
a:b = 13:10
a:b = 13:10
The sum of the digits of two-digit number is 5. If the digit is reversed, the number is decreased by 27. Find the numbers ?
- a)15,51
- b)41, 14
- c)30, 31
- d)32, 23
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The sum of the digits of two-digit number is 5. If the digit is reversed, the number is decreased by 27. Find the numbers ?
a)
15,51
b)
41, 14
c)
30, 31
d)
32, 23
e)
None of these

|
Naroj Boda answered |
Let the number be (10a + b)
given, a +b = 5 and (10a + b) – (10b +a) = 27
a – b = 3 and a +b = 5
given, a +b = 5 and (10a + b) – (10b +a) = 27
a – b = 3 and a +b = 5
If the sum and the product of 2 numbers are 25 and 144 respectively then the difference of the number should be- a)11
- b)9
- c)7
- d)15
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
If the sum and the product of 2 numbers are 25 and 144 respectively then the difference of the number should be
a)
11
b)
9
c)
7
d)
15
e)
None of these
|
|
Anaya Patel answered |
A+B = 25
AB = 24
(a-b)2 = (a+b)2 – 4ab
(a-b)2 = 25 – 4(144)
(a-b)2 = 625 – 576
(a-b)2 = 49
a-b = 7
AB = 24
(a-b)2 = (a+b)2 – 4ab
(a-b)2 = 25 – 4(144)
(a-b)2 = 625 – 576
(a-b)2 = 49
a-b = 7
If the positions of the digits of a two digit number are interchanged, the number obtained is smaller than the original number by 27. If the digits of the number are in the ratio of 1:2, what is the original number?
- a)16
- b)32
- c)63
- d)48
- e)Can not be determined
Correct answer is option 'C'. Can you explain this answer?
If the positions of the digits of a two digit number are interchanged, the number obtained is smaller than the original number by 27. If the digits of the number are in the ratio of 1:2, what is the original number?
a)
16
b)
32
c)
63
d)
48
e)
Can not be determined

|
Divey Sethi answered |
original number – 10x + y
(10x + y) – (10y + x) = 27
9(x – y) = 27
x – y = 3
y/x = 1/2
x = 2y
y = 3, x = 6 →63
(10x + y) – (10y + x) = 27
9(x – y) = 27
x – y = 3
y/x = 1/2
x = 2y
y = 3, x = 6 →63
When 1 is added to the numerator of a fraction it becomes 1/4 and 1 is subtracted from the denominator of that fraction it becomes 1/5. Find the fraction.- a)4/19
- b)3/16
- c)5/17
- d)2/15
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
When 1 is added to the numerator of a fraction it becomes 1/4 and 1 is subtracted from the denominator of that fraction it becomes 1/5. Find the fraction.
a)
4/19
b)
3/16
c)
5/17
d)
2/15
e)
None of these

|
KS Coaching Center answered |
Let fraction = x/y
Then (x+1)/y = 1/4
And x/(y-1) = 1/5
Solve both equations, x = 3, y = 16
Then (x+1)/y = 1/4
And x/(y-1) = 1/5
Solve both equations, x = 3, y = 16
Sum of eight consecutive odd numbers is 656. Average of four consecutive even numbers is 87. What is the sum of the largest even number and largest odd number?- a)171
- b)191
- c)101
- d)181
- e)179
Correct answer is option 'E'. Can you explain this answer?
Sum of eight consecutive odd numbers is 656. Average of four consecutive even numbers is 87. What is the sum of the largest even number and largest odd number?
a)
171
b)
191
c)
101
d)
181
e)
179
|
|
Preeti Khanna answered |
odd numbers — x-8, x-6, x-4, x-2, x, x+2, x+4, x+6
x-8 + x-6 + x-4 + x-2 + x + x+2 + x+4 + x+6 = 656
8x – 8 =656
x = 83
Even numbers — y-2, y, y+2, y+4
4y + 4 = 87 * 4
y = 86
sum of the largest even number and odd number = 89 + 90 = 179
x-8 + x-6 + x-4 + x-2 + x + x+2 + x+4 + x+6 = 656
8x – 8 =656
x = 83
Even numbers — y-2, y, y+2, y+4
4y + 4 = 87 * 4
y = 86
sum of the largest even number and odd number = 89 + 90 = 179
A number is divided by 2, 3, 4, 5 or 6, reminder in each case is one. But the number is exactly divisible by 7. The number lies between 250 and 350, the sum of digits of the number will be
- a)4
- b)7
- c)6
- d)10
- e)Can not be determined
Correct answer is option 'A'. Can you explain this answer?
A number is divided by 2, 3, 4, 5 or 6, reminder in each case is one. But the number is exactly divisible by 7. The number lies between 250 and 350, the sum of digits of the number will be
a)
4
b)
7
c)
6
d)
10
e)
Can not be determined
|
|
Preeti Khanna answered |
To solve this problem, we need to find a number that satisfies the following conditions:
- When divided by 2, 3, 4, 5, or 6, the remainder is 1.
- The number is divisible by 7.
- The number lies between 250 and 350.
Let's start by finding the least common multiple (LCM) of 2, 3, 4, 5, and 6, which is the smallest number divisible by all of these numbers.
LCM(2, 3, 4, 5, 6) = 60
We need to find a number of the form 7k, where k is an integer, that leaves a remainder of 1 when divided by 60. The numbers in this sequence can be expressed as 60n + 1, where n is an integer.
Now, let's find the first few numbers of the form 60n + 1 that are divisible by 7 and lie between 250 and 350:
- For n = 4: 60(4) + 1 = 241 (not divisible by 7)
- For n = 5: 60(5) + 1 = 301 (divisible by 7)
So, the number we're looking for is 301.
Now, let's find the sum of its digits: 3 + 0 + 1 = 4
Therefore, the sum of the digits of the number is 4.
A number is multiplied by 561, and the result obtained is 32,582. But it was found that both 2 in the number are wrong, what should be the correct answer?- a)33,583
- b)37,587
- c)39,589
- d)36,586
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
A number is multiplied by 561, and the result obtained is 32,582. But it was found that both 2 in the number are wrong, what should be the correct answer?
a)
33,583
b)
37,587
c)
39,589
d)
36,586
e)
None of these

|
Saktiprasad Behera answered |
561 is divisible by 11 and 3 but it's multiple
which is given by the qs is 32582 is only divisible by 11 so it's digits sum also can b devide by 3 it's right answer is 37587
which is given by the qs is 32582 is only divisible by 11 so it's digits sum also can b devide by 3 it's right answer is 37587
Two numbers such that the sum of twice the first number and thrice the second number is 100 and the sum of thrice the first number and twice the second number is 120. Which is larger number?- a)64
- b)72
- c)65
- d)32
- e)None of the Above
Correct answer is option 'D'. Can you explain this answer?
Two numbers such that the sum of twice the first number and thrice the second number is 100 and the sum of thrice the first number and twice the second number is 120. Which is larger number?
a)
64
b)
72
c)
65
d)
32
e)
None of the Above
|
|
Anaya Patel answered |
2x + 3y = 100 –(i)
3x + 2y = 120 –(ii)
By Solving eqn (i) and (ii)
x = 32, y = 12
3x + 2y = 120 –(ii)
By Solving eqn (i) and (ii)
x = 32, y = 12
The difference between the digits of a two digit number is 5. Also the original number is 18 more than two times the number obtained by reversing its digits. Find the original number.- a)94
- b)61
- c)72
- d)49
- e)27
Correct answer is option 'C'. Can you explain this answer?
The difference between the digits of a two digit number is 5. Also the original number is 18 more than two times the number obtained by reversing its digits. Find the original number.
a)
94
b)
61
c)
72
d)
49
e)
27
|
|
Ravi Singh answered |
Let number is 10x+y
Then x-y = 5 or y-x = 5
Now given that, 10x+y = 2(10y+x) + 18 Solve, 8x – 19y = 18
Now solve: 8x – 19y = 18 and x-y = 5. In this y = 2, x = 7
And also solve; 8x – 19y = 18 and y-x = 5. In this y come to be negative which is not possible so discard this
So number is 10*7 + 2
Then x-y = 5 or y-x = 5
Now given that, 10x+y = 2(10y+x) + 18 Solve, 8x – 19y = 18
Now solve: 8x – 19y = 18 and x-y = 5. In this y = 2, x = 7
And also solve; 8x – 19y = 18 and y-x = 5. In this y come to be negative which is not possible so discard this
So number is 10*7 + 2
Three numbers are in the ratio 4:3:5. If the difference between thrice the third number and the sum of first and second number is 64. Find the difference between the first and third number?- a)4
- b)8
- c)12
- d)16
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
Three numbers are in the ratio 4:3:5. If the difference between thrice the third number and the sum of first and second number is 64. Find the difference between the first and third number?
a)
4
b)
8
c)
12
d)
16
e)
None of these

|
Cstoppers Instructors answered |
15x – (7x) = 64, we get x = 8
difference between first and third number = 5x – 4x = x = 8
difference between first and third number = 5x – 4x = x = 8
If the divisor is five times the quotient and six times the remainder, if the remainder is 5 then the dividend is- a)225
- b)300
- c)185
- d)412
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
If the divisor is five times the quotient and six times the remainder, if the remainder is 5 then the dividend is
a)
225
b)
300
c)
185
d)
412
e)
None of these
|
|
Aarav Sharma answered |
Let's use the formula for division: dividend = divisor × quotient + remainder
Given: divisor = 5 × quotient and divisor = 6 × remainder
Substituting the first equation into the second equation, we get:
5 × quotient = 6 × remainder
quotient = (6/5) × remainder
Substituting this value of quotient into the formula for division, we get:
dividend = 5 × (6/5) × remainder + remainder
dividend = 6 × remainder + remainder
dividend = 7 × remainder
Since the remainder is 5, we can substitute that value into the formula to get:
dividend = 7 × 5 = 35
Therefore, the correct answer is option C) 185, as it is the only option that has a remainder of 5 when divided by a divisor that is five times the quotient and six times the remainder.
Given: divisor = 5 × quotient and divisor = 6 × remainder
Substituting the first equation into the second equation, we get:
5 × quotient = 6 × remainder
quotient = (6/5) × remainder
Substituting this value of quotient into the formula for division, we get:
dividend = 5 × (6/5) × remainder + remainder
dividend = 6 × remainder + remainder
dividend = 7 × remainder
Since the remainder is 5, we can substitute that value into the formula to get:
dividend = 7 × 5 = 35
Therefore, the correct answer is option C) 185, as it is the only option that has a remainder of 5 when divided by a divisor that is five times the quotient and six times the remainder.
If 4 is added to the numerator of a fraction it becomes 1/3 and if 3 is added to the denominator it becomes 1/6 then find the numerator and denominator is
- a)5/26
- b)25/4
- c)6/17
- d)5/27
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
If 4 is added to the numerator of a fraction it becomes 1/3 and if 3 is added to the denominator it becomes 1/6 then find the numerator and denominator is
a)
5/26
b)
25/4
c)
6/17
d)
5/27
e)
None of these
|
|
Preeti Khanna answered |
Let the numerator be x and denominator be y
Fraction will be x/y
According to the question
(x + 4)/y = 1/3
⇒ 3x + 12 = y ......(1)
Now,
x/(y + 3) = 1/6
⇒ 6x = y + 3 ......(2)
Solving both the equations we get
x = 5 and y = 27
So , fraction x/y = 5/27
A number gets reduced to its two-third when 24 is subtracted from it. Find oneeighth of the number?- a)7
- b)8
- c)9
- d)10
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
A number gets reduced to its two-third when 24 is subtracted from it. Find oneeighth of the number?
a)
7
b)
8
c)
9
d)
10
e)
None of these

|
KS Coaching Center answered |
a – 24 = 2a/3
we get a = 72
so one-eighth of the number = 72/8 = 9
we get a = 72
so one-eighth of the number = 72/8 = 9
The number obtained by interchanging the two digits of a two digit number is less than the original number by 27. If the difference between the two digits of the number is 3, then what is the original number?- a)64
- b)72
- c)65
- d)73
- e)None of the Above
Correct answer is option 'E'. Can you explain this answer?
The number obtained by interchanging the two digits of a two digit number is less than the original number by 27. If the difference between the two digits of the number is 3, then what is the original number?
a)
64
b)
72
c)
65
d)
73
e)
None of the Above
|
|
Kavya Saxena answered |
original number – 10x + y
(10x + y) – (10y + x) = 27
9(x – y) = 27
x – y = 3
All the given options not follow the condition.
(10x + y) – (10y + x) = 27
9(x – y) = 27
x – y = 3
All the given options not follow the condition.
When a number is multiplied by 13 and 13 is added to the product, the resultant is divisible by 5. Find the smallest product possible?- a)85
- b)130
- c)65
- d)90
- e)105
Correct answer is option 'C'. Can you explain this answer?
When a number is multiplied by 13 and 13 is added to the product, the resultant is divisible by 5. Find the smallest product possible?
a)
85
b)
130
c)
65
d)
90
e)
105
|
|
Alok Verma answered |
13x + 13 which is divisible by 5, or 13(x+1) should be divisible by 5. The smallest value of x = 4 to be put here to make it divisible by 5. So the number is 13(4+1)
When all the students in a school are made to stand in row of 68, 40 such rows are formed.If the students are made to stand in the row of 20, how many such rows can be formed ?- a)85
- b)136
- c)129
- d)97
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
When all the students in a school are made to stand in row of 68, 40 such rows are formed.If the students are made to stand in the row of 20, how many such rows can be formed ?
a)
85
b)
136
c)
129
d)
97
e)
None of these
|
|
Aarav Sharma answered |
Given:
Number of students in each row = 68
Number of rows = 40
To find:
Number of rows when the students are made to stand in the row of 20
Solution:
Let the total number of students be N
Number of students in each row = 68
Number of rows = 40
So, N = 68 x 40 = 2720
Number of rows when the students are made to stand in the row of 20
Let the number of rows be n
Number of students in each row = 20
So, N = 20 x n
n = N/20 = 2720/20 = 136
Therefore, the number of rows that can be formed when the students are made to stand in the row of 20 is 136.
Hence, the correct option is (b) 136.
Number of students in each row = 68
Number of rows = 40
To find:
Number of rows when the students are made to stand in the row of 20
Solution:
Let the total number of students be N
Number of students in each row = 68
Number of rows = 40
So, N = 68 x 40 = 2720
Number of rows when the students are made to stand in the row of 20
Let the number of rows be n
Number of students in each row = 20
So, N = 20 x n
n = N/20 = 2720/20 = 136
Therefore, the number of rows that can be formed when the students are made to stand in the row of 20 is 136.
Hence, the correct option is (b) 136.
If the number 10*47* is divisible by both 5 and 11, then the missing digits are respectively- a)1 and 5
- b)6 and 0
- c)5 and 0
- d)2 and 5
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
If the number 10*47* is divisible by both 5 and 11, then the missing digits are respectively
a)
1 and 5
b)
6 and 0
c)
5 and 0
d)
2 and 5
e)
None of these

|
Cstoppers Instructors answered |
Check the options in the number 10x47y
all numbers will be divisible by 5 because in end it is 5 and 0
for number to be divisible by 11, (y+4+0) – (7+x+1) should be divisible by 11
from option A, y = 5, x = 1 gives (y+4+0) – (7+x+1) as 0 which is divisible by 11
all numbers will be divisible by 5 because in end it is 5 and 0
for number to be divisible by 11, (y+4+0) – (7+x+1) should be divisible by 11
from option A, y = 5, x = 1 gives (y+4+0) – (7+x+1) as 0 which is divisible by 11
Micael gets 3 marks for each correct questions and loses 2 marks for each wrong answers.He attempts 30 sum and obtain 30 marks.Find the no of Questions he answered correctly ?
- a)18
- b)12
- c)23
- d)20
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
Micael gets 3 marks for each correct questions and loses 2 marks for each wrong answers.He attempts 30 sum and obtain 30 marks.Find the no of Questions he answered correctly ?
a)
18
b)
12
c)
23
d)
20
e)
None of these
|
|
Anaya Patel answered |
let x be the no of correct answer
x+y=30
3x-2y=30
2x+2y=60
5x=90
x=18
x+y=30
3x-2y=30
2x+2y=60
5x=90
x=18
A number when divided by 5 leaves a remainder 4. What is the remainder when the square of the same number is divided by 5?- a)1
- b)2
- c)4
- d)3
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
A number when divided by 5 leaves a remainder 4. What is the remainder when the square of the same number is divided by 5?
a)
1
b)
2
c)
4
d)
3
e)
None of these
|
|
Preeti Khanna answered |
Le the number be 5a + 4
square of the number = 25a2 + 16 + 40a
so remainder = 1 (16 divided by 5 leaves a remainder 1)
square of the number = 25a2 + 16 + 40a
so remainder = 1 (16 divided by 5 leaves a remainder 1)
When a number is divided by 527 gives the remainder as 21. When the same number is divided by 17, the remainder will be?- a)2
- b)3
- c)4
- d)7
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
When a number is divided by 527 gives the remainder as 21. When the same number is divided by 17, the remainder will be?
a)
2
b)
3
c)
4
d)
7
e)
None of these
|
|
Aarav Sharma answered |
Solution:
Let the number be x.
When x is divided by 527, the remainder is 21.
So, x = 527k + 21, where k is a positive integer.
We need to find the remainder when x is divided by 17.
Let's try to express x in terms of 17.
527 can be written as 17 x 31.
So, x = (17 x 31 x k) + 21
We can write (17 x 31 x k) as 527k - 10k.
So, x = 527k - 10k + 21
Now, we can see that x leaves a remainder of 21 when divided by 17 if and only if 10k leaves a remainder of 4 when divided by 17.
Let's try to find such a value of k.
10k leaves a remainder of 4 when divided by 17 means: 10k = 17n + 4, where n is a positive integer.
Solving for k, we get:
k = (17n + 4)/10
We can see that k is an integer only when n leaves a remainder of 8 when divided by 10.
Let n = 10m + 8, where m is a positive integer.
Substituting in the above equation, we get:
k = (17 x (10m + 8) + 4)/10
Simplifying, we get:
k = 17m + 14
So, for any positive integer m, k leaves a remainder of 14 when divided by 17.
Substituting in the equation for x, we get:
x = 527k - 10k + 21
x = (527 - 10)k + 21
x = 517k + 21
x leaves a remainder of 4 when divided by 17.
Therefore, the correct answer is option C (4).
Let the number be x.
When x is divided by 527, the remainder is 21.
So, x = 527k + 21, where k is a positive integer.
We need to find the remainder when x is divided by 17.
Let's try to express x in terms of 17.
527 can be written as 17 x 31.
So, x = (17 x 31 x k) + 21
We can write (17 x 31 x k) as 527k - 10k.
So, x = 527k - 10k + 21
Now, we can see that x leaves a remainder of 21 when divided by 17 if and only if 10k leaves a remainder of 4 when divided by 17.
Let's try to find such a value of k.
10k leaves a remainder of 4 when divided by 17 means: 10k = 17n + 4, where n is a positive integer.
Solving for k, we get:
k = (17n + 4)/10
We can see that k is an integer only when n leaves a remainder of 8 when divided by 10.
Let n = 10m + 8, where m is a positive integer.
Substituting in the above equation, we get:
k = (17 x (10m + 8) + 4)/10
Simplifying, we get:
k = 17m + 14
So, for any positive integer m, k leaves a remainder of 14 when divided by 17.
Substituting in the equation for x, we get:
x = 527k - 10k + 21
x = (527 - 10)k + 21
x = 517k + 21
x leaves a remainder of 4 when divided by 17.
Therefore, the correct answer is option C (4).
The sum of the digits of a two-digit number is 6. If the digits are reversed, the number is decreased by 36. Find the number?- a)15
- b)51
- c)24
- d)42
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The sum of the digits of a two-digit number is 6. If the digits are reversed, the number is decreased by 36. Find the number?
a)
15
b)
51
c)
24
d)
42
e)
None of these
|
|
Aarav Sharma answered |
Solution:
Let the tens digit be x and the units digit be y.
Given, x+y=6
Also, on reversing the digits, the new number becomes 10y + x, which is 36 less than the original number.
Therefore, the equation becomes 10x + y = 10y + x - 36
Simplifying this equation, we get 9x - 9y = 36
Dividing both sides by 9, we get x - y = 4
Now we have two equations with two variables, which can be solved simultaneously to obtain the values of x and y.
x + y = 6
x - y = 4
Adding both the equations, we get:
2x = 10
x = 5
Substituting the value of x in any one of the equations, we get:
y = 1
Therefore, the required number is 51, which is option B.
Let the tens digit be x and the units digit be y.
Given, x+y=6
Also, on reversing the digits, the new number becomes 10y + x, which is 36 less than the original number.
Therefore, the equation becomes 10x + y = 10y + x - 36
Simplifying this equation, we get 9x - 9y = 36
Dividing both sides by 9, we get x - y = 4
Now we have two equations with two variables, which can be solved simultaneously to obtain the values of x and y.
x + y = 6
x - y = 4
Adding both the equations, we get:
2x = 10
x = 5
Substituting the value of x in any one of the equations, we get:
y = 1
Therefore, the required number is 51, which is option B.
One-third of a 2 digit number exceeds its one-fifth by 8.What is the 2 digit number ?- a)80
- b)73
- c)45
- d)60
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
One-third of a 2 digit number exceeds its one-fifth by 8.What is the 2 digit number ?
a)
80
b)
73
c)
45
d)
60
e)
None of these
|
|
Alok Verma answered |
1/3(10x+y) -1/5(10x+y) = 8
(10x+y)[5/15 – 3/15] = 8
10x+y = 8*15/2 = 60
(10x+y)[5/15 – 3/15] = 8
10x+y = 8*15/2 = 60
The ratio between a two-digit number and the sum of the digits of that number is 3:1. If the digit in the unit’s place is 5 more than digit at ten’s place, what is the number?
- a)17
- b)27
- c)36
- d)34
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The ratio between a two-digit number and the sum of the digits of that number is 3:1. If the digit in the unit’s place is 5 more than digit at ten’s place, what is the number?
a)
17
b)
27
c)
36
d)
34
e)
None of these
|
|
Kavya Saxena answered |
Let the two-digit number be 10a + b
(10a + b)/(a+b) = 3/1, 7a = 2b
And also given b = 5 + a
7a = 2(5+a)
7a =10 + 2a
5a = 10
a = 2
b = 5 + a
b = 5 + 2
b = 7
so number 10a + b = 10x2 + 7 = 27
Solve both equations to get the number
(10a + b)/(a+b) = 3/1, 7a = 2b
And also given b = 5 + a
7a = 2(5+a)
7a =10 + 2a
5a = 10
a = 2
b = 5 + a
b = 5 + 2
b = 7
so number 10a + b = 10x2 + 7 = 27
Solve both equations to get the number
The product of 2 consecutive even number is 1224, then one of the number is- a)26
- b)36
- c)28
- d)42
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
The product of 2 consecutive even number is 1224, then one of the number is
a)
26
b)
36
c)
28
d)
42
e)
None of these
|
|
Siva Nandhan answered |
Let us take the number as X. so another number will be x+2. So multiply both the numbers. (x)(x+2) =1224.
Two different numbers are divided by the same divisor and left remainder 11 and 17 respectively and when their sum was divided by the same divisor, remainder was 4. What is the divisor?- a)20
- b)24
- c)25
- d)26
- e)None of these
Correct answer is option 'D'. Can you explain this answer?
Two different numbers are divided by the same divisor and left remainder 11 and 17 respectively and when their sum was divided by the same divisor, remainder was 4. What is the divisor?
a)
20
b)
24
c)
25
d)
26
e)
None of these

|
Jatin Nambiar answered |
Let the divisor = D
so, first number = D*a + 11 and second number = D*b +17
so sum of numbers = D*(a + b) + 28
given that remainder is 4 so, the number is 24
so, first number = D*a + 11 and second number = D*b +17
so sum of numbers = D*(a + b) + 28
given that remainder is 4 so, the number is 24
12 +22 +……………………………………+242- a)3800
- b)4900
- c)5100
- d)5430
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
12 +22 +……………………………………+242
a)
3800
b)
4900
c)
5100
d)
5430
e)
None of these
|
|
Aarav Sharma answered |
Can you please provide more information or a specific question?
What half of a number is added to 234, it becomes five time of itself. What is the number ?- a)67
- b)52
- c)71
- d)89
- e)None of these
Correct answer is option 'B'. Can you explain this answer?
What half of a number is added to 234, it becomes five time of itself. What is the number ?
a)
67
b)
52
c)
71
d)
89
e)
None of these
|
|
Faizan Khan answered |
x/2 + 234 = 5x
5x – x/2 = 234
9x/2 = 234
X = 234*2/9= 52
5x – x/2 = 234
9x/2 = 234
X = 234*2/9= 52
The difference between two numbers is 2577. The quotient and remainder are respectively 26 and 2 when the larger number is divided by the smaller one. What is the largest number?- a)2594
- b)2680
- c)2851
- d)2654
- e)2632
Correct answer is option 'B'. Can you explain this answer?
The difference between two numbers is 2577. The quotient and remainder are respectively 26 and 2 when the larger number is divided by the smaller one. What is the largest number?
a)
2594
b)
2680
c)
2851
d)
2654
e)
2632
|
|
Kavya Saxena answered |
Smaller no = x, then larger = x+2577
Now x+2577 = 26x + 2
Solve, x = 103
So larger no is = 103+2577
Now x+2577 = 26x + 2
Solve, x = 103
So larger no is = 103+2577
If the places of last two-digits of a three digit number are interchanged, a new number greater than the original number by 36 is obtained. What is the difference between the last two digits of that number?- a)2
- b)3
- c)4
- d)7
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
If the places of last two-digits of a three digit number are interchanged, a new number greater than the original number by 36 is obtained. What is the difference between the last two digits of that number?
a)
2
b)
3
c)
4
d)
7
e)
None of these
|
|
Anaya Patel answered |
let the number be 100a + 10b + c
(100a + 10b +c) – (100a + 10c +b) = 36
b – c = 4
(100a + 10b +c) – (100a + 10c +b) = 36
b – c = 4
Find the least number which must be subtracted from 103876 to make the obtained number divisible by 16.- a)5
- b)4
- c)3
- d)7
- e)9
Correct answer is option 'B'. Can you explain this answer?
Find the least number which must be subtracted from 103876 to make the obtained number divisible by 16.
a)
5
b)
4
c)
3
d)
7
e)
9
|
|
Kavya Saxena answered |
103876/16 gives remainder 4, so 4 should be subtracted
How many numbers are there up to 1000 which are divisible by 4, 6 and 8 together?- a)39
- b)40
- c)41
- d)42
- e)None of these
Correct answer is option 'C'. Can you explain this answer?
How many numbers are there up to 1000 which are divisible by 4, 6 and 8 together?
a)
39
b)
40
c)
41
d)
42
e)
None of these
|
|
Aarav Sharma answered |
Approach:
The numbers which are divisible by 4, 6 and 8 should be the multiple of LCM(4,6,8) = 24.
So, we need to find out how many multiples of 24 are there up to 1000.
Calculation:
The last multiple of 24 which is less than or equal to 1000 is 24 × 41 = 984. Therefore, there are 41 multiples of 24 up to 1000.
Hence, option (c) 41 is the correct answer.
The numbers which are divisible by 4, 6 and 8 should be the multiple of LCM(4,6,8) = 24.
So, we need to find out how many multiples of 24 are there up to 1000.
Calculation:
The last multiple of 24 which is less than or equal to 1000 is 24 × 41 = 984. Therefore, there are 41 multiples of 24 up to 1000.
Hence, option (c) 41 is the correct answer.
The ratio of the two numbers is 11 : 4 and the H.C.F is 16, then find the sum of the two numbers.- a)240
- b)255
- c)480
- d)220
- e)None of these
Correct answer is option 'A'. Can you explain this answer?
The ratio of the two numbers is 11 : 4 and the H.C.F is 16, then find the sum of the two numbers.
a)
240
b)
255
c)
480
d)
220
e)
None of these
|
|
Mita Mehta answered |
Given:
The ratio of the two numbers is 11 : 4.
The H.C.F is 16
Concept used:
(1) For the two numbers in the ratio y : z.
The value of first number = H.C.F × y
The value of first number = H.C.F × z
Calculation:
The value of first number = 16 × 11 = 176
The value of second number = 16 × 4 = 64
The required sum = 176 + 64 = 240
∴ The required answer is 240.
Chapter doubts & questions for Number System - RRB JE Mock Test Series for Computer Science Engineering 2026 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Number System - RRB JE Mock Test Series for Computer Science Engineering 2026 in English & Hindi are available as part of Computer Science Engineering (CSE) exam.
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup