All Exams >
Engineering Mathematics >
Engineering Mathematics >
All Questions
All questions of Graph Theory for Engineering Mathematics Exam
Let G be a connected planar graph with 10 vertices. If the number of edges on each face is three, then the number of edges in G is ________.
Correct answer is '24'. Can you explain this answer?
Let G be a connected planar graph with 10 vertices. If the number of edges on each face is three, then the number of edges in G is ________.
|
|
Sanya Agarwal answered |
Data:
number of faces = |F|
number of vertices = |V| = 10
edges covering each face = 3
number of faces = |F|
number of vertices = |V| = 10
edges covering each face = 3
Formula:
According to Euler’s formula :
|V| - |E| + |F| = 2
According to Euler’s formula :
|V| - |E| + |F| = 2
Calculation
edges on each face is three
∴ 2 |E| = 3 |F| (every edge is shared by 2 faces)
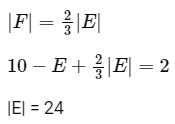
the number of edges in G is 24
edges on each face is three
∴ 2 |E| = 3 |F| (every edge is shared by 2 faces)
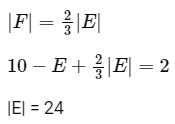
the number of edges in G is 24
A star connected network consumes a power of 20 kW with a power factor of 0.8. Calculate the value of resistance of each coil when a supply voltage of 230 volts and 50 Hz is supplied between two phases of the network.- a)8 ohms
- b)1.23 ohms
- c)1 ohm
- d)1.692 ohms
Correct answer is option 'D'. Can you explain this answer?
A star connected network consumes a power of 20 kW with a power factor of 0.8. Calculate the value of resistance of each coil when a supply voltage of 230 volts and 50 Hz is supplied between two phases of the network.
a)
8 ohms
b)
1.23 ohms
c)
1 ohm
d)
1.692 ohms
|
|
Sanya Agarwal answered |
active power (P) = 20 kW
Vph = 230 V
VL = 230√3 V
power factor (cosϕ ) = 0.8.
cosϕ = P/S
S = P\cosϕ = 20/0.8 = 25 KVA
Then;
Vph = 230 V
VL = 230√3 V
power factor (cosϕ ) = 0.8.
cosϕ = P/S
S = P\cosϕ = 20/0.8 = 25 KVA
Then;

Also
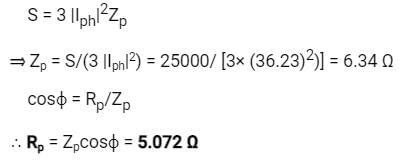
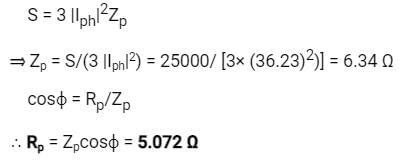
The maximum degree of any vertex in a simple graph with n vertices is- a)n
- b)n - 1
- c)n + 1
- d)2n - 1
Correct answer is option 'B'. Can you explain this answer?
The maximum degree of any vertex in a simple graph with n vertices is
a)
n
b)
n - 1
c)
n + 1
d)
2n - 1

|
Manasa Bose answered |
The maximum degree of any vertex in a simple graph with n vertices is n - 1.
Explanation:
A simple graph is a graph that does not contain any loops (edges that connect a vertex to itself) or multiple edges (more than one edge between the same pair of vertices). In other words, each edge in a simple graph connects two distinct vertices.
In a simple graph with n vertices, each vertex can be connected to at most n - 1 other vertices. This is because a vertex cannot be connected to itself, so it can have at most n - 1 neighboring vertices.
To understand why the maximum degree of any vertex is n - 1, let's consider the worst-case scenario. In this scenario, each vertex in the graph is connected to every other vertex, creating a complete graph.
Key Points:
- A complete graph is a graph in which every pair of distinct vertices is connected by an edge.
- In a complete graph with n vertices, each vertex is connected to every other vertex.
- Therefore, the degree of each vertex in a complete graph is n - 1.
Example:
Let's consider a simple graph with 5 vertices. The maximum degree of any vertex in this graph is 4 (n - 1).
(2)------(3)
| |
| |
(1)------(4)
|
(5)
In the above example, each vertex is connected to at most 4 other vertices. Therefore, the maximum degree of any vertex is 4.
Conclusion:
In a simple graph with n vertices, the maximum degree of any vertex is n - 1. This is because each vertex can be connected to at most n - 1 other vertices.
Explanation:
A simple graph is a graph that does not contain any loops (edges that connect a vertex to itself) or multiple edges (more than one edge between the same pair of vertices). In other words, each edge in a simple graph connects two distinct vertices.
In a simple graph with n vertices, each vertex can be connected to at most n - 1 other vertices. This is because a vertex cannot be connected to itself, so it can have at most n - 1 neighboring vertices.
To understand why the maximum degree of any vertex is n - 1, let's consider the worst-case scenario. In this scenario, each vertex in the graph is connected to every other vertex, creating a complete graph.
Key Points:
- A complete graph is a graph in which every pair of distinct vertices is connected by an edge.
- In a complete graph with n vertices, each vertex is connected to every other vertex.
- Therefore, the degree of each vertex in a complete graph is n - 1.
Example:
Let's consider a simple graph with 5 vertices. The maximum degree of any vertex in this graph is 4 (n - 1).
(2)------(3)
| |
| |
(1)------(4)
|
(5)
In the above example, each vertex is connected to at most 4 other vertices. Therefore, the maximum degree of any vertex is 4.
Conclusion:
In a simple graph with n vertices, the maximum degree of any vertex is n - 1. This is because each vertex can be connected to at most n - 1 other vertices.
The degree of any vertex of graph is _______.- a)The number of edges incident with vertex
- b)Number of vertex in a graph
- c)Number of vertices adjacent to that vertex
- d)Number of edges in a graph
Correct answer is option 'A'. Can you explain this answer?
The degree of any vertex of graph is _______.
a)
The number of edges incident with vertex
b)
Number of vertex in a graph
c)
Number of vertices adjacent to that vertex
d)
Number of edges in a graph
|
|
Sanvi Kapoor answered |
The number of edges connected on a vertex v with the self loop counted twice is called the degree of vertex.
Consider a 4-ary tree T consisting of 17 vertices. What is the sum of the degree of T?
Correct answer is '32'. Can you explain this answer?
Consider a 4-ary tree T consisting of 17 vertices. What is the sum of the degree of T?
|
|
Sanvi Kapoor answered |
Concept:
By using handshaking theorem of graph theory, the sum of degree of all the vertices in a tree is equal to twice the number of edges in a graph.
By using handshaking theorem of graph theory, the sum of degree of all the vertices in a tree is equal to twice the number of edges in a graph.
Formula:
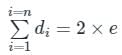
where di is the degree of vertex i and e is the total number of edges in a graph
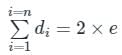
where di is the degree of vertex i and e is the total number of edges in a graph
Calculation:
For a tree,
number of edges = e = n – 1
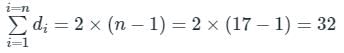
sum of the degrees of all the vertices in T is 32.
For a tree,
number of edges = e = n – 1
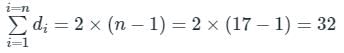
sum of the degrees of all the vertices in T is 32.
Which of the following properties of the circuits of a graph are correct? - The minimum number of branches possible in a circuit will be equal to the number of elements in a circuit.
- There are exactly two paths between any pair of vertices in a circuit.
- There are at least two branches in a circuit.
Select the correct answer using the code given below.- a)1 and 2 only
- b)1 and 3 only
- c)2 and 3 only
- d)1, 2 and 3
Correct answer is option 'B'. Can you explain this answer?
Which of the following properties of the circuits of a graph are correct?
- The minimum number of branches possible in a circuit will be equal to the number of elements in a circuit.
- There are exactly two paths between any pair of vertices in a circuit.
- There are at least two branches in a circuit.
Select the correct answer using the code given below.
a)
1 and 2 only
b)
1 and 3 only
c)
2 and 3 only
d)
1, 2 and 3

|
Sarthak Kulkarni answered |
Explanation:
In order to determine which properties of the circuits of a graph are correct, let's analyze each option:
Option 1: The minimum number of branches possible in a circuit will be equal to the number of elements in a circuit.
This statement is incorrect. The number of branches in a circuit is always greater than the number of elements. Each element in a circuit contributes at least one branch.
Option 2: There are exactly two paths between any pair of vertices in a circuit.
This statement is incorrect. A circuit is a closed loop, so there is only one path between any pair of vertices. A path refers to a sequence of edges, and in a circuit, there is only one path that connects two vertices.
Option 3: There are at least two branches in a circuit.
This statement is correct. In a circuit, there must be at least two branches to form a closed loop. A branch is a connection between two vertices, and in a circuit, there must be at least two connections to form a closed loop.
Therefore, the correct answer is Option B: 1 and 3 only.
In order to determine which properties of the circuits of a graph are correct, let's analyze each option:
Option 1: The minimum number of branches possible in a circuit will be equal to the number of elements in a circuit.
This statement is incorrect. The number of branches in a circuit is always greater than the number of elements. Each element in a circuit contributes at least one branch.
Option 2: There are exactly two paths between any pair of vertices in a circuit.
This statement is incorrect. A circuit is a closed loop, so there is only one path between any pair of vertices. A path refers to a sequence of edges, and in a circuit, there is only one path that connects two vertices.
Option 3: There are at least two branches in a circuit.
This statement is correct. In a circuit, there must be at least two branches to form a closed loop. A branch is a connection between two vertices, and in a circuit, there must be at least two connections to form a closed loop.
Therefore, the correct answer is Option B: 1 and 3 only.
Identify true statements:
(I) Every complete graph is Hamiltonian
(II) Every wheel graph is Hamiltonian
(III) Every complete bipartite graph is Hamiltonian- a)I only
- b)I and II only
- c)II only
- d)I, II and III
Correct answer is option 'C'. Can you explain this answer?
Identify true statements:
(I) Every complete graph is Hamiltonian
(II) Every wheel graph is Hamiltonian
(III) Every complete bipartite graph is Hamiltonian
(I) Every complete graph is Hamiltonian
(II) Every wheel graph is Hamiltonian
(III) Every complete bipartite graph is Hamiltonian
a)
I only
b)
I and II only
c)
II only
d)
I, II and III

|
Sonal Tiwari answered |
True Statements:
(II) Every wheel graph is Hamiltonian:
A wheel graph is formed by connecting a single central vertex to all the vertices of a cycle graph. In a wheel graph, there is a Hamiltonian cycle that visits every vertex exactly once. The cycle can start from any vertex in the outer cycle and then move to the central vertex before returning to the starting vertex. Therefore, every wheel graph is Hamiltonian.
False Statements:
(I) Every complete graph is Hamiltonian:
A complete graph is a graph in which every pair of distinct vertices is connected by an edge. While it is true that a complete graph with three or more vertices is Hamiltonian, this statement does not hold for complete graphs with one or two vertices. In a complete graph with one vertex, there is no Hamiltonian cycle as there are no other vertices to visit. In a complete graph with two vertices, there is only one edge and no Hamiltonian cycle can be formed. Therefore, not every complete graph is Hamiltonian.
(III) Every complete bipartite graph is Hamiltonian:
A complete bipartite graph is a graph in which the vertices can be partitioned into two sets such that every vertex in one set is connected to every vertex in the other set. In a complete bipartite graph, there is no Hamiltonian cycle. This can be proven by considering the number of vertices and edges in the graph. The number of vertices in a complete bipartite graph is the product of the sizes of the two sets, which can be large. On the other hand, the number of edges is the product of the sizes of the two sets, which can be much smaller. Therefore, the number of edges is significantly less than the number of vertices, making it impossible to form a Hamiltonian cycle. Therefore, not every complete bipartite graph is Hamiltonian.
Conclusion:
The only true statement is that every wheel graph is Hamiltonian. The other two statements are false, as not every complete graph or complete bipartite graph is Hamiltonian.
(II) Every wheel graph is Hamiltonian:
A wheel graph is formed by connecting a single central vertex to all the vertices of a cycle graph. In a wheel graph, there is a Hamiltonian cycle that visits every vertex exactly once. The cycle can start from any vertex in the outer cycle and then move to the central vertex before returning to the starting vertex. Therefore, every wheel graph is Hamiltonian.
False Statements:
(I) Every complete graph is Hamiltonian:
A complete graph is a graph in which every pair of distinct vertices is connected by an edge. While it is true that a complete graph with three or more vertices is Hamiltonian, this statement does not hold for complete graphs with one or two vertices. In a complete graph with one vertex, there is no Hamiltonian cycle as there are no other vertices to visit. In a complete graph with two vertices, there is only one edge and no Hamiltonian cycle can be formed. Therefore, not every complete graph is Hamiltonian.
(III) Every complete bipartite graph is Hamiltonian:
A complete bipartite graph is a graph in which the vertices can be partitioned into two sets such that every vertex in one set is connected to every vertex in the other set. In a complete bipartite graph, there is no Hamiltonian cycle. This can be proven by considering the number of vertices and edges in the graph. The number of vertices in a complete bipartite graph is the product of the sizes of the two sets, which can be large. On the other hand, the number of edges is the product of the sizes of the two sets, which can be much smaller. Therefore, the number of edges is significantly less than the number of vertices, making it impossible to form a Hamiltonian cycle. Therefore, not every complete bipartite graph is Hamiltonian.
Conclusion:
The only true statement is that every wheel graph is Hamiltonian. The other two statements are false, as not every complete graph or complete bipartite graph is Hamiltonian.
In a connected graph, a bridge is an edge whose removal disconnects a graph. Which one of the following statements is true?- a)A tree has no bridges
- b)A bridge cannot be part of a simple cycle
- c)Every edge of a clique with size ≥ 3 is a bridge (A clique is any complete sub graph of a graph)
- d)A graph with bridges cannot have a cycle
Correct answer is option 'B'. Can you explain this answer?
In a connected graph, a bridge is an edge whose removal disconnects a graph. Which one of the following statements is true?
a)
A tree has no bridges
b)
A bridge cannot be part of a simple cycle
c)
Every edge of a clique with size ≥ 3 is a bridge (A clique is any complete sub graph of a graph)
d)
A graph with bridges cannot have a cycle
|
|
Sanya Agarwal answered |
(A) FALSE:
e.g.
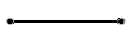
e.g.
The only edge in the above tree is bridge.
(B) TRUE:
If an edge is the part of the cycle than its removal will not disconnect the graph.
(C) FALSE:
e.g.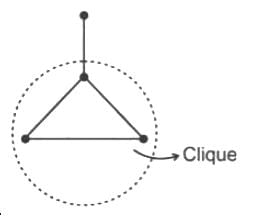
Here no edge of the clique is a bridge
(D) FALSE:
eg.
(B) TRUE:
If an edge is the part of the cycle than its removal will not disconnect the graph.
(C) FALSE:
e.g.

Here no edge of the clique is a bridge
(D) FALSE:
eg.

What is the sum of the degree of each vertex for an undirected graph with m vertices and n edges ?- a)(2n - 1)/2
- b)mn
- c)2n
- d)2m
Correct answer is option 'C'. Can you explain this answer?
What is the sum of the degree of each vertex for an undirected graph with m vertices and n edges ?
a)
(2n - 1)/2
b)
mn
c)
2n
d)
2m
|
|
Sanya Agarwal answered |
Concept:
A tree with n vertices has e edges
The Handshaking Theorem states that the sum of the degrees of all the vertices of G is twice the number of edges in G.
A tree with n vertices has e edges
The Handshaking Theorem states that the sum of the degrees of all the vertices of G is twice the number of edges in G.
Formula:
∑ di = 2 × e (By Handshaking Lemma)
∑ di = 2 × e (By Handshaking Lemma)
Explanation:
Given an undirected graph total of n edges
e=n
and ∑ di is the sum of the degree of each vertex
∑ di = 2 × e
∑ di = 2n
So, the sum of the degree of each vertex is 2n
Given an undirected graph total of n edges
e=n
and ∑ di is the sum of the degree of each vertex
∑ di = 2 × e
∑ di = 2n
So, the sum of the degree of each vertex is 2n
In what time can the Hamiltonian path problem can be solved using dynamic programming?- a)O(N)
- b)O(N log N)
- c)O(N2)
- d)O(N2 2N)
Correct answer is option 'D'. Can you explain this answer?
In what time can the Hamiltonian path problem can be solved using dynamic programming?
a)
O(N)
b)
O(N log N)
c)
O(N2)
d)
O(N2 2N)

|
Saikat Gupta answered |
The Hamiltonian path problem is a well-known problem in computer science and graph theory. It involves finding a path in a graph that visits each vertex exactly once. Dynamic programming is a technique that can be used to solve this problem efficiently.
The time complexity of solving the Hamiltonian path problem using dynamic programming depends on the number of vertices in the graph. Let's analyze the given options to understand which one is the correct answer.
a) O(N): This option suggests that the problem can be solved in linear time, where N is the number of vertices in the graph. However, finding a Hamiltonian path is known to be an NP-complete problem, which means there is no known polynomial-time algorithm for it. Therefore, option A is incorrect.
b) O(N log N): This option suggests that the problem can be solved in N log N time. However, this is not possible because the problem is NP-complete. Therefore, option B is incorrect.
c) O(N^2): This option suggests that the problem can be solved in quadratic time, where N is the number of vertices in the graph. This is a possibility because dynamic programming can be used to solve the Hamiltonian path problem in O(N^2 2^N) time. However, we need to analyze the last option to make sure it is not a better choice. Therefore, option C is a possibility but may not be the correct answer.
d) O(N^2 2^N): This option suggests that the problem can be solved in O(N^2 2^N) time, where N is the number of vertices in the graph. This is the correct answer because dynamic programming can be used to solve the Hamiltonian path problem in this time complexity. The 2^N factor is due to the exponential number of subsets of vertices that need to be considered. By using dynamic programming, we can avoid redundant computations and solve the problem efficiently. Therefore, option D is the correct answer.
To summarize, the Hamiltonian path problem can be solved using dynamic programming in O(N^2 2^N) time complexity, where N is the number of vertices in the graph. This is the correct answer to the given question.
The time complexity of solving the Hamiltonian path problem using dynamic programming depends on the number of vertices in the graph. Let's analyze the given options to understand which one is the correct answer.
a) O(N): This option suggests that the problem can be solved in linear time, where N is the number of vertices in the graph. However, finding a Hamiltonian path is known to be an NP-complete problem, which means there is no known polynomial-time algorithm for it. Therefore, option A is incorrect.
b) O(N log N): This option suggests that the problem can be solved in N log N time. However, this is not possible because the problem is NP-complete. Therefore, option B is incorrect.
c) O(N^2): This option suggests that the problem can be solved in quadratic time, where N is the number of vertices in the graph. This is a possibility because dynamic programming can be used to solve the Hamiltonian path problem in O(N^2 2^N) time. However, we need to analyze the last option to make sure it is not a better choice. Therefore, option C is a possibility but may not be the correct answer.
d) O(N^2 2^N): This option suggests that the problem can be solved in O(N^2 2^N) time, where N is the number of vertices in the graph. This is the correct answer because dynamic programming can be used to solve the Hamiltonian path problem in this time complexity. The 2^N factor is due to the exponential number of subsets of vertices that need to be considered. By using dynamic programming, we can avoid redundant computations and solve the problem efficiently. Therefore, option D is the correct answer.
To summarize, the Hamiltonian path problem can be solved using dynamic programming in O(N^2 2^N) time complexity, where N is the number of vertices in the graph. This is the correct answer to the given question.
Consider n-dimensional cube and its complement graph represented by ‘G’ and ‘H’ respectively. y × 210 edges are present in graph ‘H’ if ‘n’ is equal to 11. Find the value of y?
Correct answer is '2036'. Can you explain this answer?
Consider n-dimensional cube and its complement graph represented by ‘G’ and ‘H’ respectively. y × 210 edges are present in graph ‘H’ if ‘n’ is equal to 11. Find the value of y?
|
|
Sanya Agarwal answered |
Data:
|H| = |G| = n = 11
number of edges in H = |E| = y × 210
|H| = |G| = n = 11
number of edges in H = |E| = y × 210
Formula:
By Handshaking Lemma:
Σdi = 2 × |E|
Where di is the degree of ith vertex
|E| is the number of edges in a graph
By Handshaking Lemma:
Σdi = 2 × |E|
Where di is the degree of ith vertex
|E| is the number of edges in a graph
Calculation:
For n-dimensional cube:
Degree of vertices = n = 11
Number of vertices: 2n =211
11 × 211 =2 × |E1|
| E1| =11 × 210
For n-dimensional cube:
Degree of vertices = n = 11
Number of vertices: 2n =211
11 × 211 =2 × |E1|
| E1| =11 × 210
For complete graph:
Degree of each vertex: 211 – 1
(211 − 1) × 211 = 2 ×|E2|
| E2|= 2047 × 210
E = |E2| – |E1|
y × 210 = 2047 × 210 – 11 × 210
∴ y = 2036
Degree of each vertex: 211 – 1
(211 − 1) × 211 = 2 ×|E2|
| E2|= 2047 × 210
E = |E2| – |E1|
y × 210 = 2047 × 210 – 11 × 210
∴ y = 2036
An undirected graph G with only one simple path between each pair of vertices has two vertices of degree 4, one vertex of degree 3 and two vertices of degree 2.Number of vertices of degree 1 are ______________
Correct answer is '7'. Can you explain this answer?
An undirected graph G with only one simple path between each pair of vertices has two vertices of degree 4, one vertex of degree 3 and two vertices of degree 2.
Number of vertices of degree 1 are ______________
|
|
Sanya Agarwal answered |
Concept:
Since there is only one simple path between each pair of vertices, the given graph is a tree.
Tree with n nodes has (n -1) edges
Let the number of vertices of degree 1 be x.
2 vertices have degree 4
2 vertices have degree 2
1 vertex has degree 3
Since there is only one simple path between each pair of vertices, the given graph is a tree.
Tree with n nodes has (n -1) edges
Let the number of vertices of degree 1 be x.
2 vertices have degree 4
2 vertices have degree 2
1 vertex has degree 3
Calculation:
Total number of nodes in a graph = x + 2 + 2 + 1 = x + 5
Total number of edges in a graph = x + 5 - 1 = x + 4
According to Handshaking Lemma,
∑deg(v) = 2|E| where E is Edges.
2×4+1×3+2×2+x=2(x+4)
15 + x = 8 + 2x
∴ x = 7
Total number of nodes in a graph = x + 2 + 2 + 1 = x + 5
Total number of edges in a graph = x + 5 - 1 = x + 4
According to Handshaking Lemma,
∑deg(v) = 2|E| where E is Edges.
2×4+1×3+2×2+x=2(x+4)
15 + x = 8 + 2x
∴ x = 7
If for some positive integer k, degree of vertex d(v)=k for every vertex v of the graph G, then G is called ______.- a)K graph
- b)K-regular graph
- c)Empty graph
- d)All of above
Correct answer is option 'B'. Can you explain this answer?
If for some positive integer k, degree of vertex d(v)=k for every vertex v of the graph G, then G is called ______.
a)
K graph
b)
K-regular graph
c)
Empty graph
d)
All of above
|
|
Sanya Agarwal answered |
A graph in which all vertices are of equal degree is called regular graph.
Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices?- a)The diagonal entries of A2 are the degrees of the vertices of the graph.
- b)If the graph is connected, then none of the entries of An-1 + In can be zero.
- c)If the sum of all the elements of A is at most 2(n - 1), then the graph must be acyclic.
- d)If there is at least a 1 in each of A’s rows and columns, then the graph must be connected.
Correct answer is option 'A'. Can you explain this answer?
Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices?
a)
The diagonal entries of A2 are the degrees of the vertices of the graph.
b)
If the graph is connected, then none of the entries of An-1 + In can be zero.
c)
If the sum of all the elements of A is at most 2(n - 1), then the graph must be acyclic.
d)
If there is at least a 1 in each of A’s rows and columns, then the graph must be connected.

|
Alok Iyer answered |
A) The diagonal entries of A^2 are not necessarily the degrees of the vertices of the graph. The diagonal entries of A^2 represent the number of length-2 paths between each pair of vertices in the graph. The degrees of the vertices are represented by the diagonal entries of A.
b) If the graph is connected, then all entries of A^(n-1) + A^(n-2) + ... + A + I (where I is the identity matrix) are positive. This is known as the matrix-tree theorem, and it states that the sum of these matrices (up to A^(n-1)) gives the Laplacian matrix of the graph, and the determinant of the Laplacian matrix is equal to the number of spanning trees in the graph. Therefore, if the graph is connected, the determinant of the Laplacian matrix is non-zero, which means none of the entries of A^(n-1) + A^(n-2) + ... + A + I can be zero.
c) If the sum of all the elements of A is at most 2(n - 1), it does not necessarily mean that the graph is acyclic. The sum of all the elements of A represents the total number of edges in the graph. If this sum is at most 2(n - 1), it means that the graph has at most 2(n-1) edges, which is the maximum number of edges in a tree. However, the graph could still have cycles if it is not a tree.
d) If there is at least a 1 in each of A, then it means that each vertex is connected to at least one other vertex in the graph. This does not necessarily imply any specific property of the graph, as it could still have cycles and be a connected graph.
b) If the graph is connected, then all entries of A^(n-1) + A^(n-2) + ... + A + I (where I is the identity matrix) are positive. This is known as the matrix-tree theorem, and it states that the sum of these matrices (up to A^(n-1)) gives the Laplacian matrix of the graph, and the determinant of the Laplacian matrix is equal to the number of spanning trees in the graph. Therefore, if the graph is connected, the determinant of the Laplacian matrix is non-zero, which means none of the entries of A^(n-1) + A^(n-2) + ... + A + I can be zero.
c) If the sum of all the elements of A is at most 2(n - 1), it does not necessarily mean that the graph is acyclic. The sum of all the elements of A represents the total number of edges in the graph. If this sum is at most 2(n - 1), it means that the graph has at most 2(n-1) edges, which is the maximum number of edges in a tree. However, the graph could still have cycles if it is not a tree.
d) If there is at least a 1 in each of A, then it means that each vertex is connected to at least one other vertex in the graph. This does not necessarily imply any specific property of the graph, as it could still have cycles and be a connected graph.
Consider the following graph:
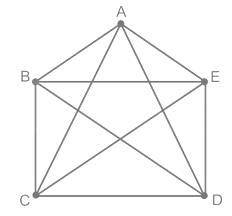 Number of Hamiltonian Cycles starting and ending at A is _______
Number of Hamiltonian Cycles starting and ending at A is _______- a)24
- b)48
- c)72
- d)120
Correct answer is option 'A'. Can you explain this answer?
Consider the following graph:


Number of Hamiltonian Cycles starting and ending at A is _______
a)
24
b)
48
c)
72
d)
120

|
Pioneer Academy answered |
Total number of H.C. in a complete graph with n vertices = n !
# H.C. starting at a particular vertex
= n! / n = (n – 1)!
Also # edge-disjoint H.C. =
: if (n - 1)!/2 is odd
0 : otherwise
# H.C. starting at a particular vertex
= n! / n = (n – 1)!
Also # edge-disjoint H.C. =
: if (n - 1)!/2 is odd
0 : otherwise
For which values of m and n does the complete bipartite graph km, n have a Hamilton circuit?- a)m ≠ n, m, n ≥ 2
- b)m ≠ n, m, n ≥ 3
- c)m = n, m, n ≥ 2
- d)m = 2, m, n ≥ 3
Correct answer is option 'C'. Can you explain this answer?
For which values of m and n does the complete bipartite graph km, n have a Hamilton circuit?
a)
m ≠ n, m, n ≥ 2
b)
m ≠ n, m, n ≥ 3
c)
m = n, m, n ≥ 2
d)
m = 2, m, n ≥ 3

|
Partho Jain answered |
For the complete bipartite graph $K_{m,n}$ to have a Hamilton circuit, we need every vertex to have degree at least 2.
The degree of each vertex in the left part of the graph is $n$, since it is connected to every vertex in the right part. Similarly, the degree of each vertex in the right part is $m$.
Therefore, we need $m \geq 2$ and $n \geq 2$ for every vertex to have degree at least 2.
If $m=1$ or $n=1$, then one of the parts of the graph only has one vertex, and thus it cannot have a Hamilton circuit.
So the answer is: $m \geq 2$ and $n \geq 2$.
The degree of each vertex in the left part of the graph is $n$, since it is connected to every vertex in the right part. Similarly, the degree of each vertex in the right part is $m$.
Therefore, we need $m \geq 2$ and $n \geq 2$ for every vertex to have degree at least 2.
If $m=1$ or $n=1$, then one of the parts of the graph only has one vertex, and thus it cannot have a Hamilton circuit.
So the answer is: $m \geq 2$ and $n \geq 2$.
The minimum number of colours that is sufficient to vertex-colour any planar graph is_______.
Correct answer is '4'. Can you explain this answer?
The minimum number of colours that is sufficient to vertex-colour any planar graph is_______.
|
|
Sanvi Kapoor answered |
According to the property of planar graph and four colour theorems. Maximum number of colours that are needed to vertex-colour any planar graph is 4.
Example:
In this graph, only 3 colours are enough to colour this planar graph.
In this graph, only 3 colours are enough to colour this planar graph.

But if in this graph, there is an edge from a to d also, then three colours are not enough to vertex-colour this graph.
In this graph, 4 colours are needed to vertex- colour this graph.
The maximum number of edges in a bipartite graph on 12 vertices is ________
Correct answer is '36'. Can you explain this answer?
The maximum number of edges in a bipartite graph on 12 vertices is ________

|
Harsh Khanna answered |
Explanation:
A bipartite graph is a graph whose vertices can be divided into two independent sets, such that every edge connects a vertex in one set to a vertex in the other set.
To find the maximum number of edges in a bipartite graph on 12 vertices, we need to consider the case where the two sets of vertices have equal size.
Let the two sets of vertices be A and B, each with 6 vertices. The maximum number of edges that can be formed between vertices in A and B is when every vertex in A is connected to every vertex in B. This gives us a total of 6 * 6 = 36 edges.
Answer: 36
A bipartite graph is a graph whose vertices can be divided into two independent sets, such that every edge connects a vertex in one set to a vertex in the other set.
To find the maximum number of edges in a bipartite graph on 12 vertices, we need to consider the case where the two sets of vertices have equal size.
Let the two sets of vertices be A and B, each with 6 vertices. The maximum number of edges that can be formed between vertices in A and B is when every vertex in A is connected to every vertex in B. This gives us a total of 6 * 6 = 36 edges.
Answer: 36
Let G = (V, E) be a directed graph where V is the set of vertices and E the set of edges. Then which one of the following graphs has the same strongly connected components as G?- a)G1 = (V, E1) where E1 = {(u, v)|(u, v) ∉ E}
- b)G2 = (V, E2) where E2 = {(u, v)|(v, u) ∈ E}
- c)G3 = (V, E3) where E3 = {(u, v)| there is a path of length ≤ 2 from u to v in E}
- d)G4 = (V4, E) where V4 is the set of vertices in G which are not isolated
Correct answer is option 'B'. Can you explain this answer?
Let G = (V, E) be a directed graph where V is the set of vertices and E the set of edges. Then which one of the following graphs has the same strongly connected components as G?
a)
G1 = (V, E1) where E1 = {(u, v)|(u, v) ∉ E}
b)
G2 = (V, E2) where E2 = {(u, v)|(v, u) ∈ E}
c)
G3 = (V, E3) where E3 = {(u, v)| there is a path of length ≤ 2 from u to v in E}
d)
G4 = (V4, E) where V4 is the set of vertices in G which are not isolated
|
|
Sanvi Kapoor answered |
In a directed graph G Strongly connected will have a path from each vertex to every other vertex.
If the direction of the edges is reverse, then also graph is strongly connected components as G
If the direction of the edges is reverse, then also graph is strongly connected components as G
Option 2: G2 = (V, E2) where E2 = {(u, v)|(v, u) ∈ E}
In this option G2, edges are reversed and hence it is a strongly connected components as similar to G
So, changing the direction of all the edges, won't change the SCC.
In this option G2, edges are reversed and hence it is a strongly connected components as similar to G
So, changing the direction of all the edges, won't change the SCC.
Who invented the inclusion-exclusion principle to solve the Hamiltonian path problem?- a)Karp
- b)Leonard Adleman
- c)Andreas Bjorklund
- d)Martello
Correct answer is option 'C'. Can you explain this answer?
Who invented the inclusion-exclusion principle to solve the Hamiltonian path problem?
a)
Karp
b)
Leonard Adleman
c)
Andreas Bjorklund
d)
Martello
|
|
Sanya Agarwal answered |
Andreas Bjorklund came up with the inclusion-exclusion principle to reduce the counting of number of Hamiltonian cycles.
If a graph (G) has no loops or parallel edges and if the number of vertices(n) in the graph is n≥3, then the graph G is Hamiltonian if
(i) deg(v) ≥n/3 for each vertex v
(ii) deg(v) + deg(w) ≥ n whenever v and w are not connected by an edge.
(iii) E (G) ≥ 1/3 (n - 1)(n - 2) + 2- a)(i) and (iii) only
- b)(ii) and (iii) only
- c)(iii) only
- d)(ii) only
Correct answer is option 'D'. Can you explain this answer?
If a graph (G) has no loops or parallel edges and if the number of vertices(n) in the graph is n≥3, then the graph G is Hamiltonian if
(i) deg(v) ≥n/3 for each vertex v
(ii) deg(v) + deg(w) ≥ n whenever v and w are not connected by an edge.
(iii) E (G) ≥ 1/3 (n - 1)(n - 2) + 2
(i) deg(v) ≥n/3 for each vertex v
(ii) deg(v) + deg(w) ≥ n whenever v and w are not connected by an edge.
(iii) E (G) ≥ 1/3 (n - 1)(n - 2) + 2
a)
(i) and (iii) only
b)
(ii) and (iii) only
c)
(iii) only
d)
(ii) only
|
|
Sanya Agarwal answered |
Hamiltonian graph:
A Hamiltonian graph is one which contain a Hamiltonian cycle. A Hamiltonian cycle is a cycle in which each vertex is visited exactly once.
A Hamiltonian graph is one which contain a Hamiltonian cycle. A Hamiltonian cycle is a cycle in which each vertex is visited exactly once.
Properties of Hamiltonian graph:
(1) A graph has a Hamiltonian circuit if each vertex has degree >=3
(2) If G= (V, E) has n>=3 vertices and every vertex has degree >=n/2, then G has a Hamilton circuit
(3) If G is a graph with n vertices and n>=3, also deg(u) + deg(v) >=n, if u and v are not connected by an edge, then G has a hamiltonion circuit.
(4) E(G) = ½(n - 1)(n - 2) + 2
(1) A graph has a Hamiltonian circuit if each vertex has degree >=3
(2) If G= (V, E) has n>=3 vertices and every vertex has degree >=n/2, then G has a Hamilton circuit
(3) If G is a graph with n vertices and n>=3, also deg(u) + deg(v) >=n, if u and v are not connected by an edge, then G has a hamiltonion circuit.
(4) E(G) = ½(n - 1)(n - 2) + 2
What is the time complexity for finding a Hamiltonian path for a graph having N vertices (using permutation)?- a)O(N!)
- b)O(N! * N)
- c)O(log N)
- d)O(N)
Correct answer is option 'B'. Can you explain this answer?
What is the time complexity for finding a Hamiltonian path for a graph having N vertices (using permutation)?
a)
O(N!)
b)
O(N! * N)
c)
O(log N)
d)
O(N)
|
|
Sanvi Kapoor answered |
For a graph having N vertices traverse the permutations in N! iterations and it traverses the permutations to see if adjacent vertices are connected or not takes N iterations (i.e.) O(N! * N).
A path is a particular subgraph consisting of an ordered sequence of branches having which of the following properties?1. At all but two of its nodes, called internal nodes, there are incident exactly two branches of the subgraph.
2. At each of the remaining two nodes, called terminal nodes, there is incident exactly one branch of the subgraph.Select the correct answer using the code given below.- a)1 only
- b)2 only
- c)Neither 1 nor 2
- d)Both 1 and 2
Correct answer is option 'D'. Can you explain this answer?
A path is a particular subgraph consisting of an ordered sequence of branches having which of the following properties?
1. At all but two of its nodes, called internal nodes, there are incident exactly two branches of the subgraph.
2. At each of the remaining two nodes, called terminal nodes, there is incident exactly one branch of the subgraph.
2. At each of the remaining two nodes, called terminal nodes, there is incident exactly one branch of the subgraph.
Select the correct answer using the code given below.
a)
1 only
b)
2 only
c)
Neither 1 nor 2
d)
Both 1 and 2
|
|
Sanvi Kapoor answered |
Path is defined as a subgraph consisting of an ordered sequence of branches with the feature that all internal nodes (or vertex) have exactly two subgraph branches.
Only one branch is incident at each of the two terminal nodes (or vertex).
Only one branch is incident at each of the two terminal nodes (or vertex).
Which of the following can be degree sequence of simple graph?
I. 2, 3, 3, 3, 3, 3, 4, 5
II. 1, 3, 3, 4, 5, 6, 6
III. 1, 1, 3, 3, 5, 6, 7
IV. 1, 2, 3, 3, 4, 5, 6 - a)I only
- b)II & IV
- c)I and IV
- d)I, II and III
Correct answer is option 'C'. Can you explain this answer?
Which of the following can be degree sequence of simple graph?
I. 2, 3, 3, 3, 3, 3, 4, 5
II. 1, 3, 3, 4, 5, 6, 6
III. 1, 1, 3, 3, 5, 6, 7
IV. 1, 2, 3, 3, 4, 5, 6
I. 2, 3, 3, 3, 3, 3, 4, 5
II. 1, 3, 3, 4, 5, 6, 6
III. 1, 1, 3, 3, 5, 6, 7
IV. 1, 2, 3, 3, 4, 5, 6
a)
I only
b)
II & IV
c)
I and IV
d)
I, II and III
|
|
Sanvi Kapoor answered |
III is not simple graph as highest degree in any simple graph with n vertices is (n-1). II is also not a simple graph because it has 7 vertices and two vertices has degree 6, hence minimum degree cannot be 1. We can use Havel-Hakimi method for I & IV. We can show II is not simple graph using Havel-Hakimi method also.
Who formulated the first ever algorithm for solving the Hamiltonian path problem?- a)Martello
- b)Monte Carlo
- c)Leonard
- d)Bellman
Correct answer is option 'A'. Can you explain this answer?
Who formulated the first ever algorithm for solving the Hamiltonian path problem?
a)
Martello
b)
Monte Carlo
c)
Leonard
d)
Bellman
|
|
Sanya Agarwal answered |
The first ever problem to solve the Hamiltonian path was the enumerative algorithm formulated by Martello.
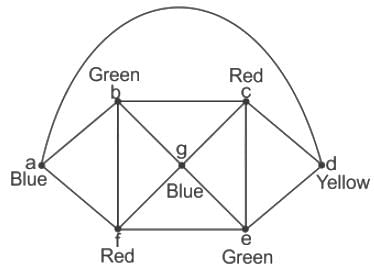
The following simple undirected graph is referred to as the Peterson graph.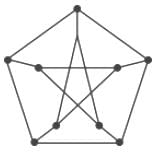 Which of the following statements is/are TRUE?
Which of the following statements is/are TRUE?- a)The chromatic number of the graph is 3.
- b)The graph has a Hamiltonian path.
- c)The following graph is isomorphic to the Peterson graph.
- d)The size of the largest independent set of the given graph is 3. (A subset of vertices of a graph form an independent set if no two vertices of the subset are adjacent.)
Correct answer is option 'A,B,C'. Can you explain this answer?
The following simple undirected graph is referred to as the Peterson graph.

Which of the following statements is/are TRUE?
a)
The chromatic number of the graph is 3.
b)
The graph has a Hamiltonian path.
c)
The following graph is isomorphic to the Peterson graph.


d)
The size of the largest independent set of the given graph is 3. (A subset of vertices of a graph form an independent set if no two vertices of the subset are adjacent.)
|
|
Sanvi Kapoor answered |
Option 1:The chromatic number of the graph is 3.
True, the Chromatic number of the Peterson graph is 3. We colour the graph with three colours (B, G, R).
True, the Chromatic number of the Peterson graph is 3. We colour the graph with three colours (B, G, R).
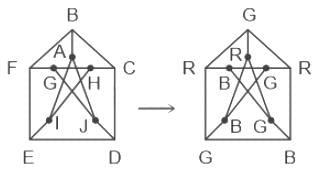
Option 2: The graph has a Hamiltonian path.
True, A Hamilton Path is a path that goes through every vertex of a graph exactly once. A Hamilton Circuit is a Hamilton path that begins and ends at the same vertex.
The Peterson graph has a Hamiltonian path but not a Hamiltonian cycle.
From above graph,
Hamiltonian path= F-B-A-I-E-D-H-G-J
True, A Hamilton Path is a path that goes through every vertex of a graph exactly once. A Hamilton Circuit is a Hamilton path that begins and ends at the same vertex.
The Peterson graph has a Hamiltonian path but not a Hamiltonian cycle.
From above graph,
Hamiltonian path= F-B-A-I-E-D-H-G-J
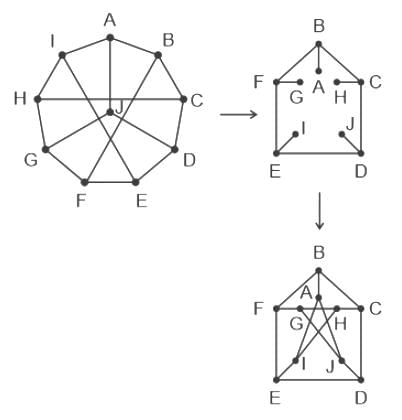
Option 3:The following graph is isomorphic to the Peterson graph.
True, If the adjacency matrices of two graphs are identical, they are said to be isomorphic or If the respective sub-graphs created by removing certain vertices of one graph and their corresponding images in the other graph are isomorphic, then the two graphs are isomorphic.
The given graph is isomorphic to Peterson's graph.
True, If the adjacency matrices of two graphs are identical, they are said to be isomorphic or If the respective sub-graphs created by removing certain vertices of one graph and their corresponding images in the other graph are isomorphic, then the two graphs are isomorphic.
The given graph is isomorphic to Peterson's graph.
Option 4: The size of the largest independent set of the given graph is 3. (A subset of vertices of a graph form an independent set if no two vertices of the subset are adjacent.)
False, A vertex independent set is a set of vertices that are not adjacent. Maximal vertex independent set is a set in which we cannot add one more vertex to it. So, the largest independent set of the Peterson graph is 4.
Hence the correct answer is options 1,2 and 3.
False, A vertex independent set is a set of vertices that are not adjacent. Maximal vertex independent set is a set in which we cannot add one more vertex to it. So, the largest independent set of the Peterson graph is 4.
Hence the correct answer is options 1,2 and 3.
How many Hamiltonian paths does the following graph have?

- a)1
- b)2
- c)0
- d)3
Correct answer is option 'C'. Can you explain this answer?
How many Hamiltonian paths does the following graph have?


a)
1
b)
2
c)
0
d)
3
|
|
Sanvi Kapoor answered |
The above graph has no Hamiltonian paths. That is, we cannot traverse the graph with meeting vertices exactly once.
If a graph (G) has no loops or parallel edges and if the number of vertices(n) in the graph is n≥3, then the graph G is Hamiltonian if
(i) deg(v) ≥n/3 for each vertex v
(ii) deg(v) + deg(w) ≥ n whenever v and w are not connected by an edge.
(iii) E (G) ≥ 1/3 (n - 1)(n - 2) + 2- a)(i) and (iii) only
- b)(ii) and (iii) only
- c)(iii) only
- d)(ii) only
Correct answer is option 'D'. Can you explain this answer?
If a graph (G) has no loops or parallel edges and if the number of vertices(n) in the graph is n≥3, then the graph G is Hamiltonian if
(i) deg(v) ≥n/3 for each vertex v
(ii) deg(v) + deg(w) ≥ n whenever v and w are not connected by an edge.
(iii) E (G) ≥ 1/3 (n - 1)(n - 2) + 2
(i) deg(v) ≥n/3 for each vertex v
(ii) deg(v) + deg(w) ≥ n whenever v and w are not connected by an edge.
(iii) E (G) ≥ 1/3 (n - 1)(n - 2) + 2
a)
(i) and (iii) only
b)
(ii) and (iii) only
c)
(iii) only
d)
(ii) only
|
|
Sanvi Kapoor answered |
Hamiltonian graph:
A Hamiltonian graph is one which contain a Hamiltonian cycle. A Hamiltonian cycle is a cycle in which each vertex is visited exactly once.
Properties of Hamiltonian graph:
(1) A graph has a Hamiltonian circuit if each vertex has degree >=3
(2) If G= (V, E) has n>=3 vertices and every vertex has degree >=n/2, then G has a Hamilton circuit
(3) If G is a graph with n vertices and n>=3, also deg(u) + deg(v) >=n, if u and v are not connected by an edge, then G has a hamiltonion circuit.
(4) E(G) = ½(n - 1)(n - 2) + 2
A Hamiltonian graph is one which contain a Hamiltonian cycle. A Hamiltonian cycle is a cycle in which each vertex is visited exactly once.
Properties of Hamiltonian graph:
(1) A graph has a Hamiltonian circuit if each vertex has degree >=3
(2) If G= (V, E) has n>=3 vertices and every vertex has degree >=n/2, then G has a Hamilton circuit
(3) If G is a graph with n vertices and n>=3, also deg(u) + deg(v) >=n, if u and v are not connected by an edge, then G has a hamiltonion circuit.
(4) E(G) = ½(n - 1)(n - 2) + 2
In an undirected graph, if we add the degrees of all vertices, it is:- a)odd
- b)even
- c)cannot be determined
- d)always n + 1, where n is number of nodes
Correct answer is option 'B'. Can you explain this answer?
In an undirected graph, if we add the degrees of all vertices, it is:
a)
odd
b)
even
c)
cannot be determined
d)
always n + 1, where n is number of nodes
|
|
Sanvi Kapoor answered |
Data:
For an undirected graph
sum of degree in a graph = dsum
number of edges in a graph = e
Formula:
By handshaking lemma:
dsum = 2 × e
Conclustion:
if e is even
dsum = 2 × even = even
if e is odd
dsum = 2 × odd = even
In an undirected graph, if we add the degrees of all vertices, it is even
For an undirected graph
sum of degree in a graph = dsum
number of edges in a graph = e
Formula:
By handshaking lemma:
dsum = 2 × e
Conclustion:
if e is even
dsum = 2 × even = even
if e is odd
dsum = 2 × odd = even
In an undirected graph, if we add the degrees of all vertices, it is even
The degree sequence of a simple graph is the sequence of the degree of the nodes in the graph in decreasing order. Which of the following sequence can be the degree sequence of any graph?
I. 4 7 1 6 3 4 6 2
II. 3 3 3 3 3 3
III. 5 4 6 7 6 3 6 5- a)Only I
- b)Only I and II
- c)Only II and III
- d)I, II and III
Correct answer is option 'C'. Can you explain this answer?
The degree sequence of a simple graph is the sequence of the degree of the nodes in the graph in decreasing order. Which of the following sequence can be the degree sequence of any graph?
I. 4 7 1 6 3 4 6 2
II. 3 3 3 3 3 3
III. 5 4 6 7 6 3 6 5
I. 4 7 1 6 3 4 6 2
II. 3 3 3 3 3 3
III. 5 4 6 7 6 3 6 5
a)
Only I
b)
Only I and II
c)
Only II and III
d)
I, II and III
|
|
Sanya Agarwal answered |
Havel Hakimi procedure:
Sequence I: 4 7 1 6 3 4 6 2

Sequence II: 3 3 3 3 3 3
Sequence I: 4 7 1 6 3 4 6 2

Sequence II: 3 3 3 3 3 3

Sequence III: 5 4 6 7 6 3 6 5

II and III can be possible sequence of degree of some graph.
Chapter doubts & questions for Graph Theory - Engineering Mathematics 2025 is part of Engineering Mathematics exam preparation. The chapters have been prepared according to the Engineering Mathematics exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Engineering Mathematics 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Graph Theory - Engineering Mathematics in English & Hindi are available as part of Engineering Mathematics exam.
Download more important topics, notes, lectures and mock test series for Engineering Mathematics Exam by signing up for free.
Engineering Mathematics
65 videos|133 docs|94 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily









