All Exams >
Engineering Mathematics >
Engineering Mathematics >
All Questions
All questions of Propositional Logic for Engineering Mathematics Exam
P: The population of Hyderabad is more than Delhi.
Q: Last year, the number of months with 31 days are 7.
choose the correct option based on the truth value of the statements?- a)P→Q is True
- b)(P→Q)→ Q is False
- c)Q→ (P→Q )is False
- d)¬(P→Q) is True
Correct answer is option 'A'. Can you explain this answer?
P: The population of Hyderabad is more than Delhi.
Q: Last year, the number of months with 31 days are 7.
choose the correct option based on the truth value of the statements?
Q: Last year, the number of months with 31 days are 7.
choose the correct option based on the truth value of the statements?
a)
P→Q is True
b)
(P→Q)→ Q is False
c)
Q→ (P→Q )is False
d)
¬(P→Q) is True

|
Kavya Mehta answered |
The correct option based on the truth value of the statements is:
a) P is true, Q is false.
a) P is true, Q is false.
If p = a number from {8, 9, 10, 11, 12}
q = not a composite number
r = a square number
s = a prime number
then what is the value of ~((p → ~q)∧(~r ∨~S) )- a)8, 9, 10, 11, 12
- b)8, 9, 10
- c)11, 12
- d)11
Correct answer is option 'D'. Can you explain this answer?
If p = a number from {8, 9, 10, 11, 12}
q = not a composite number
r = a square number
s = a prime number
then what is the value of ~((p → ~q)∧(~r ∨~S) )
q = not a composite number
r = a square number
s = a prime number
then what is the value of ~((p → ~q)∧(~r ∨~S) )
a)
8, 9, 10, 11, 12
b)
8, 9, 10
c)
11, 12
d)
11
|
|
Sanya Agarwal answered |
Given that, If p = a number from {8, 9, 10, 11, 12}
q = not a composite number
r = a square number
s = a prime number
~((p→~ q)∧(~r ∨~S) )
¬((p→¬q)∧(¬r∨¬S))
¬(¬p∨¬q)∨¬(¬r∨¬S)
(p∧q)∨(r∧s)
p∧ q = {8, 9, 10, 11, 12} ∧ {11 } = {11}
(r ∧ s) = { a square number }∧{ a prime number}
(r ∧ s) = {9} ∧ {11} = { }
(p∧ q) ∨ (r ∧ s)= {11} ∨ { } = {11}
Hence the correct answer is 11.
q = not a composite number
r = a square number
s = a prime number
~((p→~ q)∧(~r ∨~S) )
¬((p→¬q)∧(¬r∨¬S))
¬(¬p∨¬q)∨¬(¬r∨¬S)
(p∧q)∨(r∧s)
p∧ q = {8, 9, 10, 11, 12} ∧ {11 } = {11}
(r ∧ s) = { a square number }∧{ a prime number}
(r ∧ s) = {9} ∧ {11} = { }
(p∧ q) ∨ (r ∧ s)= {11} ∨ { } = {11}
Hence the correct answer is 11.
Let Q(x) be the statement “x < 5.” What is the truth value of the quantification ∀xQ(x), having domains as real numbers.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
Let Q(x) be the statement “x < 5.” What is the truth value of the quantification ∀xQ(x), having domains as real numbers.
a)
True
b)
False

|
Diya Sarkar answered |
It seems like you have not completed your question. Could you please provide the complete statement of Q(x)?
Let P(x) denote the statement “x = x + 7.” What is the truth value of the quantification ∃xP(x), where the domain consists of all real numbers?- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
Let P(x) denote the statement “x = x + 7.” What is the truth value of the quantification ∃xP(x), where the domain consists of all real numbers?
a)
True
b)
False

|
Rhea Dasgupta answered |
I apologize, but you did not provide the complete statement. Could you please provide the complete statement for P(x)?
Given the following two statements:
S1: Every table with two single-valued attributes is in 1NF, 2NF, 3NF and BCNF.
S2: AB → C, D → E, E → C is a minimal cover for the set of functional dependencies AB → C, D → E, AB → E, E → C.
Which one of the following is CORRECT?- a)S1 is TRUE and S2 is FALSE
- b)Both S1 and S2 are TRUE.
- c)S1 is FALSE and S2 is TRUE
- d)Both S1 and S2 are FALSE
Correct answer is option 'A'. Can you explain this answer?
Given the following two statements:
S1: Every table with two single-valued attributes is in 1NF, 2NF, 3NF and BCNF.
S2: AB → C, D → E, E → C is a minimal cover for the set of functional dependencies AB → C, D → E, AB → E, E → C.
Which one of the following is CORRECT?
S1: Every table with two single-valued attributes is in 1NF, 2NF, 3NF and BCNF.
S2: AB → C, D → E, E → C is a minimal cover for the set of functional dependencies AB → C, D → E, AB → E, E → C.
Which one of the following is CORRECT?
a)
S1 is TRUE and S2 is FALSE
b)
Both S1 and S2 are TRUE.
c)
S1 is FALSE and S2 is TRUE
d)
Both S1 and S2 are FALSE

|
Moumita Dasgupta answered |
Explanation:
S1: Every table with two single-valued attributes is in 1NF, 2NF, 3NF and BCNF
- This statement is FALSE.
- A table with two single-valued attributes may not necessarily be in 3NF or BCNF.
- For a table to be in 3NF, it should be in 1NF and 2NF first, and for a table to be in BCNF, it should be in 3NF.
- Therefore, S1 is incorrect.
S2: AB → C, D → E, E → C is a minimal cover for the set of functional dependencies AB → C, D → E, AB → E, E → C
- This statement is TRUE.
- A minimal cover for a set of functional dependencies is a set of dependencies that is both minimal and logically equivalent to the original set.
- In this case, the given set of functional dependencies AB → C, D → E, E → C can be simplified to AB → C, D → E, E → C.
- Therefore, S2 is correct.
Therefore, the correct answer is option 'A' where S1 is FALSE and S2 is TRUE.
S1: Every table with two single-valued attributes is in 1NF, 2NF, 3NF and BCNF
- This statement is FALSE.
- A table with two single-valued attributes may not necessarily be in 3NF or BCNF.
- For a table to be in 3NF, it should be in 1NF and 2NF first, and for a table to be in BCNF, it should be in 3NF.
- Therefore, S1 is incorrect.
S2: AB → C, D → E, E → C is a minimal cover for the set of functional dependencies AB → C, D → E, AB → E, E → C
- This statement is TRUE.
- A minimal cover for a set of functional dependencies is a set of dependencies that is both minimal and logically equivalent to the original set.
- In this case, the given set of functional dependencies AB → C, D → E, E → C can be simplified to AB → C, D → E, E → C.
- Therefore, S2 is correct.
Therefore, the correct answer is option 'A' where S1 is FALSE and S2 is TRUE.
Given a relation schema R(ABCDEFGH) in first normal form. For the set of dependencies
F= { A → B, A → C, CG → H, B → H, G → F}, which dependency is logically implied?
AC → H- a)AC → H
- b)C → H
- c)G → H
- d)A → H
Correct answer is option 'D'. Can you explain this answer?
Given a relation schema R(ABCDEFGH) in first normal form. For the set of dependencies
F= { A → B, A → C, CG → H, B → H, G → F}, which dependency is logically implied?
AC → H
F= { A → B, A → C, CG → H, B → H, G → F}, which dependency is logically implied?
AC → H
a)
AC → H
b)
C → H
c)
G → H
d)
A → H
|
|
Sanya Agarwal answered |
Concept:
If A → B and B → C then A → C is logically implied to A → B and B → C FDs this is nothing but transitivity rule.
If A → B and B → C then A → C is logically implied to A → B and B → C FDs this is nothing but transitivity rule.
Explanation:
A → B
B → H
Then we can say that A->H which is logically implied by above both FDs
So option 4 is the correct answer.
A → B
B → H
Then we can say that A->H which is logically implied by above both FDs
So option 4 is the correct answer.
Which of the following is correct?
F1 : (p ↔ q)∧(¬ p ↔ q)
F2 : (p∨¬q)∧(¬ p∨q) ∧(¬ p∨¬q)- a)F1 is satisfiable, F2 is valid
- b)F1 is unsatisfiable, F2 is satisfiable
- c)F1 is unsatisfiable, F2 is valid
- d)F1 and F2 both are unsatisfiable
Correct answer is option 'B'. Can you explain this answer?
Which of the following is correct?
F1 : (p ↔ q)∧(¬ p ↔ q)
F2 : (p∨¬q)∧(¬ p∨q) ∧(¬ p∨¬q)
F1 : (p ↔ q)∧(¬ p ↔ q)
F2 : (p∨¬q)∧(¬ p∨q) ∧(¬ p∨¬q)
a)
F1 is satisfiable, F2 is valid
b)
F1 is unsatisfiable, F2 is satisfiable
c)
F1 is unsatisfiable, F2 is valid
d)
F1 and F2 both are unsatisfiable
|
|
Sanvi Kapoor answered |
Satisfiable: A compound proposition that is not a contradiction is said to be satisfiable.
Tautology (Valid): A compound proposition that is always true is called tautology (valid).
Contradiction: A compound proposition that is always false is called a contradiction.
F1 : (p ↔ q)∧(¬ p ↔ q)
We know that ¬ (p ↔ q)= (¬ p ↔ q)
So, if (p ↔ q) is assumed of A.
Then A∧¬A = 0 or False
Means (p ↔ q)∧(¬ p ↔ q) is unsatisfiable.
F2 : (p∨¬q)∧(¬ p∨q) ∧(¬ p∨¬q)
= (p+q¯)(p¯+q)(p¯+q¯)
= (p+q¯)(p¯+qq¯)
= (p+q¯)(p¯)
= p¯q¯
Which is not valid but satisfiable.
So, F1 is unsatisfiable but F2 is satisfiable.
Hence the correct answer is F1 is unsatisfiable, F2 is satisfiable.
Tautology (Valid): A compound proposition that is always true is called tautology (valid).
Contradiction: A compound proposition that is always false is called a contradiction.
F1 : (p ↔ q)∧(¬ p ↔ q)
We know that ¬ (p ↔ q)= (¬ p ↔ q)
So, if (p ↔ q) is assumed of A.
Then A∧¬A = 0 or False
Means (p ↔ q)∧(¬ p ↔ q) is unsatisfiable.
F2 : (p∨¬q)∧(¬ p∨q) ∧(¬ p∨¬q)
= (p+q¯)(p¯+q)(p¯+q¯)
= (p+q¯)(p¯+qq¯)
= (p+q¯)(p¯)
= p¯q¯
Which is not valid but satisfiable.
So, F1 is unsatisfiable but F2 is satisfiable.
Hence the correct answer is F1 is unsatisfiable, F2 is satisfiable.
Let P (x) denote the statement “x >7.” Which of these have truth value true?- a)P (0)
- b)P (4)
- c)P (6)
- d)P (9)
Correct answer is option 'D'. Can you explain this answer?
Let P (x) denote the statement “x >7.” Which of these have truth value true?
a)
P (0)
b)
P (4)
c)
P (6)
d)
P (9)
|
|
Sanvi Kapoor answered |
Clarification: Put x = 9, 9 > 7 which is true.
Consider the relation schema: Singer(singerName, songName). What is the highest normal form satisfied by the "Singer" relation schema?- a)1NF
- b)2NF
- c)BCNF
- d)3NF
Correct answer is option 'C'. Can you explain this answer?
Consider the relation schema: Singer(singerName, songName). What is the highest normal form satisfied by the "Singer" relation schema?
a)
1NF
b)
2NF
c)
BCNF
d)
3NF
|
|
Sanya Agarwal answered |
Concept:
Normalization: Normalization is a database design technique that reduces data redundancy and eliminates undesirable characteristics like Insertion, Update and Deletion Anomalies.
Normalization: Normalization is a database design technique that reduces data redundancy and eliminates undesirable characteristics like Insertion, Update and Deletion Anomalies.
1NF (First Normal Form):
- Each table cell should contain a single value.
- Each record needs to be unique.
2NF (Second Normal Form):
- It should be in 1NF.
- Single Column Primary Key that does not functionally dependant on any subset of candidate key relation.
3NF (Third Normal Form):
- It should be in 2NF.
- It has no transitive functional dependencies.
Boyce-Codd Normal Form (BCNF):
- A relation R is in BCNF if R is in Third Normal Form and for every FD, LHS is super key.
- A relation is in BCNF iff in every non-trivial functional dependency X –> Y, X is a super key.
The given relation schema:
Singer(singerName, songName).
Singer(singerName, songName).
- Every Binary Relation ( a Relation with only 2 attributes ) is always in BCNF. If a relation is BCNF then it should be in 3NF, 2NF, 1NF.
Hence Singer(singerName, songName) is Boyce-Codd Normal Form (BCNF).
Hence the correct answer is BCNF.
Hence the correct answer is BCNF.
What is logically equivalent to the following statements? "I pass only if you pass" (Note that fail is equivalent to not pass.)- a)You pass only if I pass
- b)If you fail then I fail
- c)If you pass then I pass
- d)You fail if I pass.
Correct answer is option 'B'. Can you explain this answer?
What is logically equivalent to the following statements? "I pass only if you pass" (Note that fail is equivalent to not pass.)
a)
You pass only if I pass
b)
If you fail then I fail
c)
If you pass then I pass
d)
You fail if I pass.

|
Mira Mishra answered |
Without knowing the specific statements, it is not possible to determine what is logically equivalent to them. Please provide the statements you are referring to.
Consider a relational table R that is in 3NF, but not in BCNF, Which one of the following statements is TRUE?- a)R has a nontrivial functional dependency X → A, where X is not a superkey and A is a prime attribute.
- b)R has a nontrivial functional dependency X → A, where X is not a superkey and A is a non-prime attribute and X is not a proper subset of any key.
- c)R has a nontrivial functional dependency X → A, where X is not a superkey and A is a non-prime attribute and X is a proper subset of some key.
- d)A cell in R holds a set instead of an atomic value.
Correct answer is option 'A'. Can you explain this answer?
Consider a relational table R that is in 3NF, but not in BCNF, Which one of the following statements is TRUE?
a)
R has a nontrivial functional dependency X → A, where X is not a superkey and A is a prime attribute.
b)
R has a nontrivial functional dependency X → A, where X is not a superkey and A is a non-prime attribute and X is not a proper subset of any key.
c)
R has a nontrivial functional dependency X → A, where X is not a superkey and A is a non-prime attribute and X is a proper subset of some key.
d)
A cell in R holds a set instead of an atomic value.

|
Subham Unni answered |
B)R has a candidate key that is a proper subset of some other candidate key.
c)R has a transitive dependency that is not in BCNF.
d)R has a nontrivial functional dependency that is not in BCNF.
The correct answer is c) R has a transitive dependency that is not in BCNF.
3NF guarantees that there are no nontrivial transitive dependencies in the table, but it does not guarantee that there are no nontrivial functional dependencies. BCNF, on the other hand, guarantees that there are no nontrivial functional dependencies. So, if a table is in 3NF but not in BCNF, it must have a transitive dependency that is not in BCNF.
c)R has a transitive dependency that is not in BCNF.
d)R has a nontrivial functional dependency that is not in BCNF.
The correct answer is c) R has a transitive dependency that is not in BCNF.
3NF guarantees that there are no nontrivial transitive dependencies in the table, but it does not guarantee that there are no nontrivial functional dependencies. BCNF, on the other hand, guarantees that there are no nontrivial functional dependencies. So, if a table is in 3NF but not in BCNF, it must have a transitive dependency that is not in BCNF.
Which of the following is/are the type(s) of normal forms to which reduction can be performed?- a)Disjunctive Normal Form
- b)Conjunctive Normal Form
- c)Both A and B
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
Which of the following is/are the type(s) of normal forms to which reduction can be performed?
a)
Disjunctive Normal Form
b)
Conjunctive Normal Form
c)
Both A and B
d)
None of the above
|
|
Sanvi Kapoor answered |
The following are the types of normal forms to which reduction can be performed -
- Disjunctive Normal Form
- Conjunctive Normal Form
Let p, q, r, s represents the following propositions.
p: x ∈ {8, 9, 10, 11, 12}
q: x is a composite number
r: x is a perfect square
s: x is a prime number
The integer x ≥ 2 which satisfies ¬ ((p ⇒ q) ∧ (¬ r ∨ ¬ s)) is __________
Correct answer is '11'. Can you explain this answer?
Let p, q, r, s represents the following propositions.
p: x ∈ {8, 9, 10, 11, 12}
q: x is a composite number
r: x is a perfect square
s: x is a prime number
The integer x ≥ 2 which satisfies ¬ ((p ⇒ q) ∧ (¬ r ∨ ¬ s)) is __________
p: x ∈ {8, 9, 10, 11, 12}
q: x is a composite number
r: x is a perfect square
s: x is a prime number
The integer x ≥ 2 which satisfies ¬ ((p ⇒ q) ∧ (¬ r ∨ ¬ s)) is __________
|
|
Sanvi Kapoor answered |
Data:
p: x ∈ {8, 9, 10, 11, 12}
q: x is a composite number
r: x is a perfect square
s: x is a prime number
Explanation:
p ⇒ q means p̅ + q
As, q is composite number So, p ⇒ results in {8, 9, 10, 12}
As, r: x is a perfect square, ¬ r results in all the numbers which are not perfect square
So, ¬ r: {8, 10, 11, 12}
¬ s: {8, 9, 10, 12}
¬ r ∨ ¬ s = {8, 9, 10, 11, 12}
Now, (p ⇒ q) ∧ (¬ r ∨ ¬ s) = {8, 9, 10, 12}
¬ ((p ⇒ q) ∧ (¬ r ∨ ¬ s)) results in a number which is not present in ((p ⇒ q) ∧ (¬ r ∨ ¬ s))
¬ ((p ⇒ q) ∧ (¬ r ∨ ¬s)) will give {11}.
p: x ∈ {8, 9, 10, 11, 12}
q: x is a composite number
r: x is a perfect square
s: x is a prime number
Explanation:
p ⇒ q means p̅ + q
As, q is composite number So, p ⇒ results in {8, 9, 10, 12}
As, r: x is a perfect square, ¬ r results in all the numbers which are not perfect square
So, ¬ r: {8, 10, 11, 12}
¬ s: {8, 9, 10, 12}
¬ r ∨ ¬ s = {8, 9, 10, 11, 12}
Now, (p ⇒ q) ∧ (¬ r ∨ ¬ s) = {8, 9, 10, 12}
¬ ((p ⇒ q) ∧ (¬ r ∨ ¬ s)) results in a number which is not present in ((p ⇒ q) ∧ (¬ r ∨ ¬ s))
¬ ((p ⇒ q) ∧ (¬ r ∨ ¬s)) will give {11}.
Consider a relation R (A, B, C, D, E, F, G, H), where each attribute is atomic, and following functional dependencies exist.
CH → G
A → BC
B → CFH
E → A
F → EG
The relation R is ______.- a)in 1NF but not in 2NF
- b)in 2NF but not in 3NF
- c)in 3NF but not in BCNF
- d)in BCNF
Correct answer is option 'A'. Can you explain this answer?
Consider a relation R (A, B, C, D, E, F, G, H), where each attribute is atomic, and following functional dependencies exist.
CH → G
A → BC
B → CFH
E → A
F → EG
The relation R is ______.
CH → G
A → BC
B → CFH
E → A
F → EG
The relation R is ______.
a)
in 1NF but not in 2NF
b)
in 2NF but not in 3NF
c)
in 3NF but not in BCNF
d)
in BCNF
|
|
Sanvi Kapoor answered |
Since attribute D is not a part of any FD, it must be a part of the candidate key.
AD+ = {ABCDEFGH}
BD+ = {ABCDEFGH}
ED+ = {ABCDEFGH}
FD+ = {ABCDEFGH}
CD+, GD+, and HD+ do not all the attributes. So, they can not be candidate keys.
Candidate keys are AD, BD, ED, and FD.
A → BC, B → CFH, and F → EG are partial dependencies. So, the relation is not in 2NF.
Hence the relation is in 1NF but not in 2NF.
AD+ = {ABCDEFGH}
BD+ = {ABCDEFGH}
ED+ = {ABCDEFGH}
FD+ = {ABCDEFGH}
CD+, GD+, and HD+ do not all the attributes. So, they can not be candidate keys.
Candidate keys are AD, BD, ED, and FD.
A → BC, B → CFH, and F → EG are partial dependencies. So, the relation is not in 2NF.
Hence the relation is in 1NF but not in 2NF.
Consider the following logical inferences.
I1: If it rains then the cricket match will not be played.
The cricket match was played.
Inference: There was no rain.I2: If it rains then the cricket match will not be played.
It did not rain
Inference: The cricket match was played.Which of the following is TRUE?- a)Both I1 and I2 are correct inferences
- b)I1 is correct but I2 is not a correct inference
- c)I1 is not correct but I2 is a correct inference
- d)Both I1 and I2 are not correct inferences
Correct answer is option 'B'. Can you explain this answer?
Consider the following logical inferences.
I1: If it rains then the cricket match will not be played.
The cricket match was played.
Inference: There was no rain.
I1: If it rains then the cricket match will not be played.
The cricket match was played.
Inference: There was no rain.
I2: If it rains then the cricket match will not be played.
It did not rain
Inference: The cricket match was played.
It did not rain
Inference: The cricket match was played.
Which of the following is TRUE?
a)
Both I1 and I2 are correct inferences
b)
I1 is correct but I2 is not a correct inference
c)
I1 is not correct but I2 is a correct inference
d)
Both I1 and I2 are not correct inferences
|
|
Sanya Agarwal answered |
I1 states that:
Statement
Consider A = it rains,
B = match played
So, If (it rains) then (match will not be played) that means,
A → (¬ B)
Inference states that “there was no rain” means A = false (F)
Therefore, for any F → (¬ B) i.e. for any "F that implies not B" is true.
So this inference is valid.
Here the only condition is if it rains the match will not be played. That doesn’t mean if it will not rain then the match will be played.
If the match was played then it means it doesn’t rain.
So this inference is valid.
Statement
Consider A = it rains,
B = match played
So, If (it rains) then (match will not be played) that means,
A → (¬ B)
Inference states that “there was no rain” means A = false (F)
Therefore, for any F → (¬ B) i.e. for any "F that implies not B" is true.
So this inference is valid.
Here the only condition is if it rains the match will not be played. That doesn’t mean if it will not rain then the match will be played.
If the match was played then it means it doesn’t rain.
So this inference is valid.
I2 states that:
Statement
Consider A = it rains,
B = match played
So, If (it rains) then (match will not be played) that means,
A → (¬ B)
Inference states that “the match was played”.
Here the only condition is if it rains the match will not be played. If the match was played then it means it doesn’t rain.
That doesn’t mean if it will not rain then the match will be played.
So this inference is invalid.
Hence, the correct answer is "option b".
Statement
Consider A = it rains,
B = match played
So, If (it rains) then (match will not be played) that means,
A → (¬ B)
Inference states that “the match was played”.
Here the only condition is if it rains the match will not be played. If the match was played then it means it doesn’t rain.
That doesn’t mean if it will not rain then the match will be played.
So this inference is invalid.
Hence, the correct answer is "option b".
Full form of DNF is -?- a)Disjoining Normal Form
- b)Disjunctive Normal Form
- c)Divisional Normal Form
- d)Dividend Normal Form
Correct answer is option 'B'. Can you explain this answer?
Full form of DNF is -?
a)
Disjoining Normal Form
b)
Disjunctive Normal Form
c)
Divisional Normal Form
d)
Dividend Normal Form

|
Poulomi Patel answered |
Understanding DNF: Disjunctive Normal Form
Disjunctive Normal Form (DNF) is a standard way of structuring logical expressions in Boolean algebra. It is essential in various fields, including computer science, digital logic design, and civil engineering when analyzing logical systems.
Definition of DNF
- DNF is a canonical form of a logical formula.
- It is defined as a disjunction (OR operation) of one or more conjunctions (AND operations) of literals.
Components of DNF
- **Literals**: These are the basic variables or their negations.
- **Conjunctions**: Groups of literals combined using the AND operator.
- **Disjunctions**: The overall expression combines multiple conjunctions using the OR operator.
Characteristics of DNF
- **Clarity**: DNF allows for a clear and systematic representation of logical expressions.
- **Simplicity**: It simplifies the process of evaluating logical statements.
- **Versatility**: DNF can represent any Boolean function, making it a universal format.
Example of DNF
Consider the logical expression:
- A AND B OR C AND D.
This expression is in DNF because it is a sum of products, where:
- (A AND B) and (C AND D) are conjunctions, and they are combined by the OR operator.
Applications in Civil Engineering
In civil engineering, DNF can be used in:
- **Decision Analysis**: Analyzing various project outcomes based on different conditions.
- **Logic Circuits**: Designing digital circuits that require specific logical functions.
In summary, Disjunctive Normal Form is a fundamental concept in logic and engineering disciplines, providing a clear and structured way to handle logical expressions.
Disjunctive Normal Form (DNF) is a standard way of structuring logical expressions in Boolean algebra. It is essential in various fields, including computer science, digital logic design, and civil engineering when analyzing logical systems.
Definition of DNF
- DNF is a canonical form of a logical formula.
- It is defined as a disjunction (OR operation) of one or more conjunctions (AND operations) of literals.
Components of DNF
- **Literals**: These are the basic variables or their negations.
- **Conjunctions**: Groups of literals combined using the AND operator.
- **Disjunctions**: The overall expression combines multiple conjunctions using the OR operator.
Characteristics of DNF
- **Clarity**: DNF allows for a clear and systematic representation of logical expressions.
- **Simplicity**: It simplifies the process of evaluating logical statements.
- **Versatility**: DNF can represent any Boolean function, making it a universal format.
Example of DNF
Consider the logical expression:
- A AND B OR C AND D.
This expression is in DNF because it is a sum of products, where:
- (A AND B) and (C AND D) are conjunctions, and they are combined by the OR operator.
Applications in Civil Engineering
In civil engineering, DNF can be used in:
- **Decision Analysis**: Analyzing various project outcomes based on different conditions.
- **Logic Circuits**: Designing digital circuits that require specific logical functions.
In summary, Disjunctive Normal Form is a fundamental concept in logic and engineering disciplines, providing a clear and structured way to handle logical expressions.
Consider the following two statements.
S1: If a candidate is known to be corrupt, then he will not be elected
S2: If a candidate is kind, he will be elected
Which one of the following statements follows from S1 and S2 as per sound inference rules of logic?- a)If a person is known to be corrupt, he is kind
- b)If a person is not known to be corrupt, he is not kind
- c)If a person is kind, he is not known to be corrupt
- d)If a person is not kind, he is not known to be corrupt
Correct answer is option 'C'. Can you explain this answer?
Consider the following two statements.
S1: If a candidate is known to be corrupt, then he will not be elected
S2: If a candidate is kind, he will be elected
Which one of the following statements follows from S1 and S2 as per sound inference rules of logic?
S1: If a candidate is known to be corrupt, then he will not be elected
S2: If a candidate is kind, he will be elected
Which one of the following statements follows from S1 and S2 as per sound inference rules of logic?
a)
If a person is known to be corrupt, he is kind
b)
If a person is not known to be corrupt, he is not kind
c)
If a person is kind, he is not known to be corrupt
d)
If a person is not kind, he is not known to be corrupt
|
|
Sanvi Kapoor answered |
Concept:
Hypothetical syllogism,
If p → q and q → r then p → r
Formula:
p → q ≡ ¬ q → ¬ p ≡ ¬ p ∨ q
Hypothetical syllogism,
If p → q and q → r then p → r
Formula:
p → q ≡ ¬ q → ¬ p ≡ ¬ p ∨ q
Explanation:
C(x): x is known to be corrupt
E(x): x will be elected
K(x): x is kind
Statement S1 can be written as:
S1 ≡ C(x) → ¬E(x)
S2 can be written as:
S2 ≡ K(x) → E(x) ≡ ¬E(x) →¬K(x)
By using hypothetical syllogism,
From S1 and S2, the conclusion is
C(x) → ¬K(x) ≡ K(x) → ¬C(x)
If a person is kind, then he is not known to be corrupt.
C(x): x is known to be corrupt
E(x): x will be elected
K(x): x is kind
Statement S1 can be written as:
S1 ≡ C(x) → ¬E(x)
S2 can be written as:
S2 ≡ K(x) → E(x) ≡ ¬E(x) →¬K(x)
By using hypothetical syllogism,
From S1 and S2, the conclusion is
C(x) → ¬K(x) ≡ K(x) → ¬C(x)
If a person is kind, then he is not known to be corrupt.
p is the proposition “ Indian army moves back”
q is the proposition “ Chinese army moves back”
r is the proposition “ There is no war”
Then what is the contrapositive of the statement “ If Indian army moves back and Chinese army moves back, then there is no war”- a)~r→(~p→~q)
- b)r→(p∧q)
- c)~(p∧q)→~r
- d)~r→~(p∧q)
Correct answer is option 'D'. Can you explain this answer?
p is the proposition “ Indian army moves back”
q is the proposition “ Chinese army moves back”
r is the proposition “ There is no war”
Then what is the contrapositive of the statement “ If Indian army moves back and Chinese army moves back, then there is no war”
q is the proposition “ Chinese army moves back”
r is the proposition “ There is no war”
Then what is the contrapositive of the statement “ If Indian army moves back and Chinese army moves back, then there is no war”
a)
~r→(~p→~q)
b)
r→(p∧q)
c)
~(p∧q)→~r
d)
~r→~(p∧q)

|
Kavya Mehta answered |
It seems that the statement you provided is incomplete. Could you please provide the complete proposition?
“If X, then Y unless Z” is represented by which of the following formulae in propositional logic?
(“¬” is negation “^” is conjunction, and “→” is implication)- a) (X ^ ¬ Z) → Y
- b) (X ^ Y) → ¬ Z
- c) (X → (Y ^ ¬ Z)
- d) (X → Y(^ ¬ Z)
Correct answer is option 'A'. Can you explain this answer?
“If X, then Y unless Z” is represented by which of the following formulae in propositional logic?
(“¬” is negation “^” is conjunction, and “→” is implication)
(“¬” is negation “^” is conjunction, and “→” is implication)
a)
(X ^ ¬ Z) → Y
b)
(X ^ Y) → ¬ Z
c)
(X → (Y ^ ¬ Z)
d)
(X → Y(^ ¬ Z)
|
|
Sanya Agarwal answered |
The statement “If X then Y unless Z” means, if Z doesn’t occur, X implies Y i.e. ¬Z→(X→Y), which is equivalent to Z ∨ (X→Y)
(since P→Q ≡ ¬P ∨ Q), which is then equivalent to Z ∨ (¬X ∨ Y). Now we can look into options which one matches with this.
So option (a) is (X∧¬Z)→Y = ¬( (X∧¬Z) ) ∨ Y = (¬X∨Z) ∨ Y, which matches our expression. So option (A) is correct.
The statement, “At least one of your friends is perfect”. Let P (x) be “x is perfect” and let F (x) be “x is your friend” and let the domain be all people.- a)∀x (F (x) → P (x))
- b)∀x (F (x) ∧ P (x))
- c)∃x (F (x) ∧ P (x))
- d)∃x (F (x) → P (x))
Correct answer is option 'C'. Can you explain this answer?
The statement, “At least one of your friends is perfect”. Let P (x) be “x is perfect” and let F (x) be “x is your friend” and let the domain be all people.
a)
∀x (F (x) → P (x))
b)
∀x (F (x) ∧ P (x))
c)
∃x (F (x) ∧ P (x))
d)
∃x (F (x) → P (x))
|
|
Sanvi Kapoor answered |
Clarification: For some x, x is friend and funny.
Let the set of functional dependencies F = {QR → S, R → P, S → Q} hold on a relation schema X = (PQRS). X is not in BCNF. Suppose X is decomposed into two schemas Y and Z, where Y = (PR) and Z = (QRS).
Consider the two statements given below.
I. Both Y and Z are in BCNF
II. Decomposition of X into Y and Z is dependency preserving and lossless
Which of the above statements is/are correct?- a)Both I and II
- b)I only
- c)II only
- d)Neither I nor II
Correct answer is option 'C'. Can you explain this answer?
Let the set of functional dependencies F = {QR → S, R → P, S → Q} hold on a relation schema X = (PQRS). X is not in BCNF. Suppose X is decomposed into two schemas Y and Z, where Y = (PR) and Z = (QRS).
Consider the two statements given below.
I. Both Y and Z are in BCNF
II. Decomposition of X into Y and Z is dependency preserving and lossless
Which of the above statements is/are correct?
Consider the two statements given below.
I. Both Y and Z are in BCNF
II. Decomposition of X into Y and Z is dependency preserving and lossless
Which of the above statements is/are correct?
a)
Both I and II
b)
I only
c)
II only
d)
Neither I nor II

|
Vertex Academy answered |
X = (PQRS)
Set of functional dependencies
F = {QR → S, R → P, S → Q}
QR → {Q, R, S, P}
SR → {S, R, P, Q}
QR and SR are keys of Relation schema X
R → P …
part of key (R) → non key(P)
It is partial dependency and hence not in 2nd normal form and therefore not in BCNF (Given)
X is decomposed into two schemas Y and Z, where Y = (PR) and Z = (QRS)
For Y = (PR)
R → P
Y is in BCNF because binary attribute (R is a key).
For Z = (QRS)
QR → S
S → Q
SR → {R, S, Q}
QR → {R, Q, S}
QR and SR are keys of Relation schema X
Z is not in BCNF because
S → Q and S is not Super key.
∴ statement I is incorrect
Dependency Preserving:
R → P is in Y
QR → S in Z
S → Q is in Z
Hence, it is dependency preserving.
Lossless:
Y ∩ Z = R which is key of Y.
Therefore, it is Lossless
Statement II is correct.
Hence, option 3 is the answer
Determine the truth value of statement ∃n (4n = 3n) if the domain consists of all integers.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
Determine the truth value of statement ∃n (4n = 3n) if the domain consists of all integers.
a)
True
b)
False
|
|
Sanvi Kapoor answered |
Clarification: For n = 0, 4n = 3n hence, it is true.
Let domain of m includes all students, P (m) be the statement “m spends more than 2 hours in playing polo”. Express ∀m ¬P (m) quantification in English.- a)A student is there who spends more than 2 hours in playing polo
- b)There is a student who does not spend more than 2 hours in playing polo
- c)All students spends more than 2 hours in playing polo
- d)No student spends more than 2 hours in playing polo
Correct answer is option 'D'. Can you explain this answer?
Let domain of m includes all students, P (m) be the statement “m spends more than 2 hours in playing polo”. Express ∀m ¬P (m) quantification in English.
a)
A student is there who spends more than 2 hours in playing polo
b)
There is a student who does not spend more than 2 hours in playing polo
c)
All students spends more than 2 hours in playing polo
d)
No student spends more than 2 hours in playing polo
|
|
Sanvi Kapoor answered |
Clarification: There is no student who spends more than 2 hours in playing polo.
Determine the truth value of ∀n(n + 1 > n) if the domain consists of all real numbers.- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
Determine the truth value of ∀n(n + 1 > n) if the domain consists of all real numbers.
a)
True
b)
False
|
|
Sanya Agarwal answered |
Clarification: There are no elements in the domain for which the statement is false.
Let R (x) denote the statement “x > 2.” What is the truth value of the quantification ∃xR(x), having domain as real numbers?- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
Let R (x) denote the statement “x > 2.” What is the truth value of the quantification ∃xR(x), having domain as real numbers?
a)
True
b)
False
|
|
Sanya Agarwal answered |
Clarification: Because “x > 2” is sometimes true—for instance, when x = 3–the existential quantification of R(x), which is ∃xR(x), is true.
How many types of normal forms are there to which reduction can be performed?- a)2
- b)3
- c)4
- d)5
Correct answer is option 'A'. Can you explain this answer?
How many types of normal forms are there to which reduction can be performed?
a)
2
b)
3
c)
4
d)
5
|
|
Sanvi Kapoor answered |
There are 2 types of normal forms in which reduction can be performed.
”Everyone wants to learn cosmology.” This argument may be true for which domains?- a)All students in your cosmology class
- b)All the cosmology learning students in the world
- c)Both of the mentioned
- d)None of the mentioned
Correct answer is option 'C'. Can you explain this answer?
”Everyone wants to learn cosmology.” This argument may be true for which domains?
a)
All students in your cosmology class
b)
All the cosmology learning students in the world
c)
Both of the mentioned
d)
None of the mentioned
|
|
Sanvi Kapoor answered |
Clarification: Domain may be limited to your class or may be whole world both are good as it satisfies universal quantifier.
If the truth table cannot be created, we consider the ____ to normal forms as an alternative?- a)Addition
- b)Subtraction
- c)Reduction
- d)Division
Correct answer is option 'C'. Can you explain this answer?
If the truth table cannot be created, we consider the ____ to normal forms as an alternative?
a)
Addition
b)
Subtraction
c)
Reduction
d)
Division
|
|
Sanya Agarwal answered |
If the truth table cannot be created, we consider the reduction to normal forms as an alternative.
The statement,” Every comedian is funny” where C(x) is “x is a comedian” and F (x) is “x is funny” and the domain consists of all people.- a)∃x(C(x) ∧ F (x))
- b)∀x(C(x) ∧ F (x))
- c)∃x(C(x) → F (x))
- d)∀x(C(x) → F (x))
Correct answer is option 'D'. Can you explain this answer?
The statement,” Every comedian is funny” where C(x) is “x is a comedian” and F (x) is “x is funny” and the domain consists of all people.
a)
∃x(C(x) ∧ F (x))
b)
∀x(C(x) ∧ F (x))
c)
∃x(C(x) → F (x))
d)
∀x(C(x) → F (x))
|
|
Sanya Agarwal answered |
Clarification: For every person x, if comedian then x is funny.
Let p, q, and r be propositions and the expression (p → q) → r be a contradiction. Then the expression (r → p) → q is- a)A tautology
- b)A contradiction.
- c)Always TRUE when p is FALSE
- d)Always TRUE when q is TRUE
Correct answer is option 'D'. Can you explain this answer?
Let p, q, and r be propositions and the expression (p → q) → r be a contradiction. Then the expression (r → p) → q is
a)
A tautology
b)
A contradiction.
c)
Always TRUE when p is FALSE
d)
Always TRUE when q is TRUE
|
|
Sanya Agarwal answered |
(p → q) → r is a contradiction which is possible only when r is false and (p → q) is true.
Now, from here we can clearly say that option 4 is correct as (r → p) → q means ¬ (r → p) ∨ q.
Since r is false, (r → p) is true and ¬ (r → p) becomes false.
So, it becomes (false ∨ q). Now it totally depends on q. Whenever q is true, this value will always be true.
Alternate Method:
Let X ≡ p → q, Y ≡ (p → q) → r ≡ X → r,
Z ≡ r → p and W ≡ (r → p) → q ≡ Z → p
Using Truth table
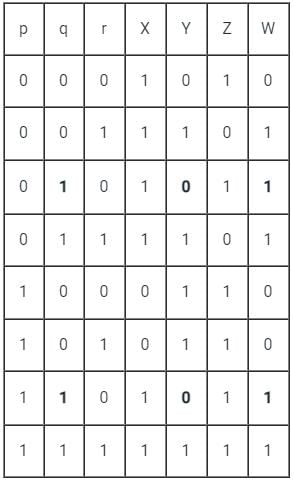
So, from truth table also, it is clear that (r → p) → q is always true when q is true, and Y is false.
Now, from here we can clearly say that option 4 is correct as (r → p) → q means ¬ (r → p) ∨ q.
Since r is false, (r → p) is true and ¬ (r → p) becomes false.
So, it becomes (false ∨ q). Now it totally depends on q. Whenever q is true, this value will always be true.
Alternate Method:
Let X ≡ p → q, Y ≡ (p → q) → r ≡ X → r,
Z ≡ r → p and W ≡ (r → p) → q ≡ Z → p
Using Truth table

So, from truth table also, it is clear that (r → p) → q is always true when q is true, and Y is false.
Chapter doubts & questions for Propositional Logic - Engineering Mathematics 2025 is part of Engineering Mathematics exam preparation. The chapters have been prepared according to the Engineering Mathematics exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Engineering Mathematics 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Propositional Logic - Engineering Mathematics in English & Hindi are available as part of Engineering Mathematics exam.
Download more important topics, notes, lectures and mock test series for Engineering Mathematics Exam by signing up for free.
Engineering Mathematics
65 videos|133 docs|94 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup









