All Exams >
Engineering Mathematics >
Engineering Mathematics >
All Questions
All questions of Numerical Methods for Engineering Mathematics Exam
Find the sum of the value of x, y, & z by using gauss jordan method.
3x - y + 2z = 12
x + 2y + 3z = 11
2x - 2y - z = 2- a)4
- b)5
- c)6
- d)7
Correct answer is option 'C'. Can you explain this answer?
Find the sum of the value of x, y, & z by using gauss jordan method.
3x - y + 2z = 12
x + 2y + 3z = 11
2x - 2y - z = 2
3x - y + 2z = 12
x + 2y + 3z = 11
2x - 2y - z = 2
a)
4
b)
5
c)
6
d)
7

|
Alok Iyer answered |
I'm sorry, but there is no equation or information given to solve for the sum of x, y, and z. Please provide more information or the equation to solve.
In an assessment conducted by Class III teacher Ms. Avni, she found out that a majority of her students have difficulty in identifying correct place value and face value. What could not be the possible reason for this misconception?- a)Many young children have difficulty with place value because it is abstract. Young children are concrete learners, they need sensory experiences to develop their learning.
- b)It is important to help children connect the concept of place value to the real world. Often, children do not see how mathematical concepts apply to their individual lives.
- c)Teachers may have difficulty teaching place value if they do not personally understand those concepts hence leading misconception in students.
- d)Carelessness and short attention span of students in class when Ms. Avni was teaching the concept of place value and face value.
Correct answer is option 'D'. Can you explain this answer?
In an assessment conducted by Class III teacher Ms. Avni, she found out that a majority of her students have difficulty in identifying correct place value and face value. What could not be the possible reason for this misconception?
a)
Many young children have difficulty with place value because it is abstract. Young children are concrete learners, they need sensory experiences to develop their learning.
b)
It is important to help children connect the concept of place value to the real world. Often, children do not see how mathematical concepts apply to their individual lives.
c)
Teachers may have difficulty teaching place value if they do not personally understand those concepts hence leading misconception in students.
d)
Carelessness and short attention span of students in class when Ms. Avni was teaching the concept of place value and face value.
|
|
Sanvi Kapoor answered |
Mathematics includes all branches of knowledge and all walks of life as it occupies an important place in all civilizations, past, and present, throughout the world.
- The teaching of mathematics should be done to promote the practical usability of mathematics and to minimize the error performed by children while using mathematical operations.
- Assessment refers to all those activities undertaken by teachers and by their students in assessing themselves that provide information to be used as feedback to modify teaching and learning activities.
Key Points
Misconception is based on the view that it is incorrect due to faulty thinking or judgment. They tend to be consistent and arise from a student's understanding of the concept.
Misconception is based on the view that it is incorrect due to faulty thinking or judgment. They tend to be consistent and arise from a student's understanding of the concept.
- Place value: It is the basis of our entire number system. This is the system in which the position of a digit in a number determines its value.
- Face value: It is the digit itself within a number.
Here, the teacher has assessed that the majority of students are having difficulty in place value and face value. This misconception could be due to the following reasons:
- Many young children have difficulty with place value because it is abstract. Young children are concrete learners, meaning they need sensory experiences to develop their learning. Using different blocks can help students to connect abstractly with concrete representation.
- It is important to help children to connect the concept of place value to the real world. Often, children do not see how mathematical concepts apply to their individual lives. This can be done by giving real-world examples.
- Teachers may have difficulty teaching place value if they do not personally understand those concepts hence leading misconceptions in students. Teachers must have a thorough understanding of the concepts before teaching to the students.
Thus, it is concluded that the carelessness and short attention span of students in class when Ms. Avni was teaching the concept of place value and face value could not be the possible reason for this misconception.
Hint
Hint
- Errors are mistakes that are made due to a short attention span, and carelessness so it is not a misconception. When a student can’t master a topic, he/she is vulnerable to make errors. Errors are nothing but incorrectness made by a student during learning.
If dy/dx = x - y2 and y(0) = 1, then y(0.1) correct upto two decimal places (approx.) is:- a)0.85
- b)0.84
- c)0.91
- d)1.01
Correct answer is option 'B'. Can you explain this answer?
If dy/dx = x - y2 and y(0) = 1, then y(0.1) correct upto two decimal places (approx.) is:
a)
0.85
b)
0.84
c)
0.91
d)
1.01

|
Prerna Menon answered |
Given:
$\frac{dy}{dx} = x - y^2$
$y(0) = 1$
To Find:
$y(0.1)$ correct up to two decimal places.
Explanation:
To solve this differential equation, we can use the method of separation of variables.
Separating the variables, we get:
$\frac{dy}{1-y^2} = x \, dx$
Integration:
Integrating both sides with respect to their respective variables, we get:
$\int{\frac{dy}{1-y^2}} = \int{x \, dx}$
LHS Integration:
To integrate the left-hand side, we can use partial fraction decomposition. The general form of the partial fraction decomposition is:
$\frac{A}{y-1} + \frac{B}{y+1}$
Multiplying through by the common denominator $(y-1)(y+1)$, we get:
$1 = A(y+1) + B(y-1)$
Expanding and equating the coefficients of like terms, we get:
$1 = (A + B)y + (A - B)$
Comparing the coefficients of 'y', we get:
$A + B = 0 \implies A = -B$
Comparing the constants, we get:
$A - B = 1$
Solving these equations, we find:
$A = \frac{1}{2}$ and $B = -\frac{1}{2}$
Substituting these values back into the partial fraction decomposition, we get:
$\frac{\frac{1}{2}}{y-1} - \frac{\frac{1}{2}}{y+1}$
Integrating each term separately, we get:
$\frac{1}{2}\ln|y-1| - \frac{1}{2}\ln|y+1|$
RHS Integration:
Integrating the right-hand side, we get:
$\int{x \, dx} = \frac{x^2}{2} + C_1$
Combining the Integrals:
Substituting the integrals back into the original equation, we get:
$\frac{1}{2}\ln|y-1| - \frac{1}{2}\ln|y+1| = \frac{x^2}{2} + C_1$
Simplifying the equation, we get:
$\ln\left|\frac{y-1}{y+1}\right| = x^2 + C_1$
Applying Initial Condition:
Now, we can apply the initial condition $y(0) = 1$.
Plugging in the values, we get:
$\ln\left|\frac{1-1}{1+1}\right| = 0^2 + C_1$
Simplifying, we get:
$\ln\left|\frac{0}{2}\right| = C_1$
Which further simplifies to:
$\ln(0) = C_1$
The natural logarithm of 0 is undefined. Therefore, $C_1$ is undefined.
Solving for y:
Now, we can solve the equation for y.
Taking the exponent of both sides, we get:
$\frac{dy}{dx} = x - y^2$
$y(0) = 1$
To Find:
$y(0.1)$ correct up to two decimal places.
Explanation:
To solve this differential equation, we can use the method of separation of variables.
Separating the variables, we get:
$\frac{dy}{1-y^2} = x \, dx$
Integration:
Integrating both sides with respect to their respective variables, we get:
$\int{\frac{dy}{1-y^2}} = \int{x \, dx}$
LHS Integration:
To integrate the left-hand side, we can use partial fraction decomposition. The general form of the partial fraction decomposition is:
$\frac{A}{y-1} + \frac{B}{y+1}$
Multiplying through by the common denominator $(y-1)(y+1)$, we get:
$1 = A(y+1) + B(y-1)$
Expanding and equating the coefficients of like terms, we get:
$1 = (A + B)y + (A - B)$
Comparing the coefficients of 'y', we get:
$A + B = 0 \implies A = -B$
Comparing the constants, we get:
$A - B = 1$
Solving these equations, we find:
$A = \frac{1}{2}$ and $B = -\frac{1}{2}$
Substituting these values back into the partial fraction decomposition, we get:
$\frac{\frac{1}{2}}{y-1} - \frac{\frac{1}{2}}{y+1}$
Integrating each term separately, we get:
$\frac{1}{2}\ln|y-1| - \frac{1}{2}\ln|y+1|$
RHS Integration:
Integrating the right-hand side, we get:
$\int{x \, dx} = \frac{x^2}{2} + C_1$
Combining the Integrals:
Substituting the integrals back into the original equation, we get:
$\frac{1}{2}\ln|y-1| - \frac{1}{2}\ln|y+1| = \frac{x^2}{2} + C_1$
Simplifying the equation, we get:
$\ln\left|\frac{y-1}{y+1}\right| = x^2 + C_1$
Applying Initial Condition:
Now, we can apply the initial condition $y(0) = 1$.
Plugging in the values, we get:
$\ln\left|\frac{1-1}{1+1}\right| = 0^2 + C_1$
Simplifying, we get:
$\ln\left|\frac{0}{2}\right| = C_1$
Which further simplifies to:
$\ln(0) = C_1$
The natural logarithm of 0 is undefined. Therefore, $C_1$ is undefined.
Solving for y:
Now, we can solve the equation for y.
Taking the exponent of both sides, we get:
Newton-Gregory Forward interpolation formula can be used ____- a)only for equally spaced intervals
- b)only for unequally spaced intervals
- c)for both equally and unequally spaced intervals
- d)for unequally intervals
Correct answer is option 'A'. Can you explain this answer?
Newton-Gregory Forward interpolation formula can be used ____
a)
only for equally spaced intervals
b)
only for unequally spaced intervals
c)
for both equally and unequally spaced intervals
d)
for unequally intervals
|
|
Anjana Singh answered |
Newton–Gregory Forward Interpolation formula is given by
f(x) = y0 + nΔy0 + n(n-1)Δ2y0/2! + n(n-1)(n-2) Δ3y0 /3! + …..
This formula is obtained by the Newton’s Divided difference formula by substituting the intervals as h. This is done because we assume the intervals to be constant, that is, equally spaced.
f(x) = y0 + nΔy0 + n(n-1)Δ2y0/2! + n(n-1)(n-2) Δ3y0 /3! + …..
This formula is obtained by the Newton’s Divided difference formula by substituting the intervals as h. This is done because we assume the intervals to be constant, that is, equally spaced.
Using Newton’s Forward formula, find sin(0.1604) from the following table.

- a)0.169713084
- b)0.159713084
- c)0.158713084
- d)0.168713084
Correct answer is option 'B'. Can you explain this answer?
Using Newton’s Forward formula, find sin(0.1604) from the following table.


a)
0.169713084
b)
0.159713084
c)
0.158713084
d)
0.168713084
|
|
Anjana Singh answered |
Here,
x0 = 0.160
x = 0.1604
h = 0.001
x = x0 + nh,
0.1604 = 0.160 + n(0.001)
n = 0.4

y0 is 0.1593182066 since it is forward interpolation formula.
Δy0 = 9.871475*10-4
Δ2y0 = -1.604*10-7
Substituting in the formula,
f(x) = y0 + nΔy0 + n(n-1)Δ2y0/2! + n(n-1)(n-2) Δ3y0 /3! ,
f(0.1604) = 0.1593182066+(0.4)(9.871475*10-4)+(0.4)(-0.6)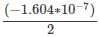
= 0.159713084.
x0 = 0.160
x = 0.1604
h = 0.001
x = x0 + nh,
0.1604 = 0.160 + n(0.001)
n = 0.4

y0 is 0.1593182066 since it is forward interpolation formula.
Δy0 = 9.871475*10-4
Δ2y0 = -1.604*10-7
Substituting in the formula,
f(x) = y0 + nΔy0 + n(n-1)Δ2y0/2! + n(n-1)(n-2) Δ3y0 /3! ,
f(0.1604) = 0.1593182066+(0.4)(9.871475*10-4)+(0.4)(-0.6)
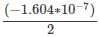
= 0.159713084.
Find f(0.18) from the following table using Newton’s Forward interpolation formula.

- a)1.18878784
- b)1.8878784
- c)1.9878785
- d)0.8878784
Correct answer is option 'A'. Can you explain this answer?
Find f(0.18) from the following table using Newton’s Forward interpolation formula.


a)
1.18878784
b)
1.8878784
c)
1.9878785
d)
0.8878784
|
|
Anjana Singh answered |
Here,
x0 = 0
x = 0.18
h = 0.1
x = x0 + nh,
0.18 = 0 + n(0.1)
n = 1.8
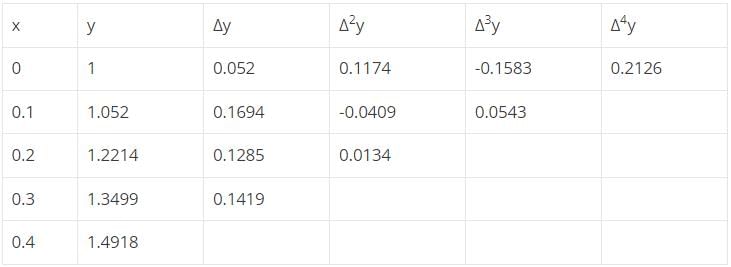
y0 is 1 since it is forward interpolation formula.
Δy0 = 0.052
Δ2y0 = 0.1174
Δ3y0 = -0.1583
Δ4y0 = 0.2126
Substituting in the formula,
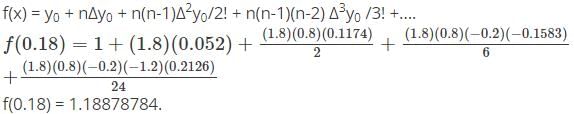
x0 = 0
x = 0.18
h = 0.1
x = x0 + nh,
0.18 = 0 + n(0.1)
n = 1.8

y0 is 1 since it is forward interpolation formula.
Δy0 = 0.052
Δ2y0 = 0.1174
Δ3y0 = -0.1583
Δ4y0 = 0.2126
Substituting in the formula,
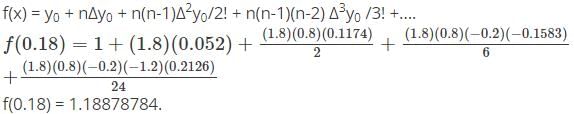
By Lagrange’s mean value theorem which of the following statement is true:
(a) If a curve has a tangent at each of its points then there exists at least one-point C on this curve, the tangent at which is parallel to chord AB
(b) If f’(x) = 0 in the interval then f(x) has same value for every value of x in (a, b)- a)(a) alone is true
- b)(b) alone is true
- c)Both (a) and (b) are true
- d)Neither (a) nor (b) is true
Correct answer is option 'A'. Can you explain this answer?
By Lagrange’s mean value theorem which of the following statement is true:
(a) If a curve has a tangent at each of its points then there exists at least one-point C on this curve, the tangent at which is parallel to chord AB
(b) If f’(x) = 0 in the interval then f(x) has same value for every value of x in (a, b)
(a) If a curve has a tangent at each of its points then there exists at least one-point C on this curve, the tangent at which is parallel to chord AB
(b) If f’(x) = 0 in the interval then f(x) has same value for every value of x in (a, b)
a)
(a) alone is true
b)
(b) alone is true
c)
Both (a) and (b) are true
d)
Neither (a) nor (b) is true
|
|
Anjana Singh answered |
Concept:
Lagrange’s Mean Value Theorem:
If f(x) is real valued function such that –
Lagrange’s Mean Value Theorem:
If f(x) is real valued function such that –
- f(x) is continuous in the closed interval [a,b]
- (f(x) is differentiable in the open interval (a,b)
- f(a) ≠ f(b)
Then there exist at least one value x, c (a,b) such that –
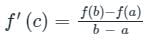
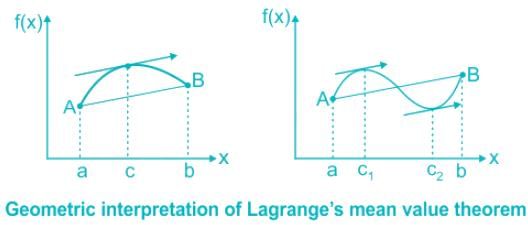
Geometrical Interpretation:
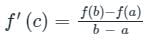

Geometrical Interpretation:
- Between two points a and b, f(a) ≠ f(b) of the graph of f(x) then there exists one point where the tangent is parallel to the chord
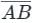
Explanation:
(a) is true with reference to geometrical interpretations.
(b) is false, if f(x) has same value for every value of x, it will violate f(a) ≠ f(b).
(a) is true with reference to geometrical interpretations.
(b) is false, if f(x) has same value for every value of x, it will violate f(a) ≠ f(b).
Trapezoidal Rule gives exact value of the integral when the integrand is a- a)linear function
- b)quadratic function
- c)cubic function
- d)polynomial of any degree
Correct answer is option 'A'. Can you explain this answer?
Trapezoidal Rule gives exact value of the integral when the integrand is a
a)
linear function
b)
quadratic function
c)
cubic function
d)
polynomial of any degree

|
Srestha Datta answered |
Introduction:
The Trapezoidal Rule is a numerical integration method that approximates the definite integral of a function by dividing the area under the curve into trapezoids. This method is simple to implement and provides a good approximation for smooth functions.
Explanation:
The Trapezoidal Rule can give an exact value of the integral when the integrand is a linear function. In this case, the function can be represented by a straight line, and the area under the curve can be accurately calculated using the trapezoidal approximation.
Reasoning:
The Trapezoidal Rule approximates the area under the curve by dividing it into trapezoids. Each trapezoid is formed by connecting two adjacent points on the curve with a straight line segment. The area of each trapezoid is then calculated by taking the average of the heights of the two adjacent points and multiplying it by the width of the trapezoid.
When the integrand is a linear function, the curve is a straight line. In this case, the Trapezoidal Rule accurately approximates the area under the curve by dividing it into trapezoids with equal widths. Since the function is linear, the heights of the trapezoids remain constant throughout the interval, and the trapezoidal approximation becomes exact.
Example:
Let's consider the linear function f(x) = 2x + 3 over the interval [1, 5]. Using the Trapezoidal Rule, we divide the interval into n subintervals and approximate the integral as follows:
∫[1, 5] (2x + 3) dx ≈ Δx/2 * [f(x0) + 2f(x1) + 2f(x2) + ... + 2f(xn-1) + f(xn)]
where Δx = (b - a)/n is the width of each subinterval, x0 = 1, xn = 5, and xi = a + iΔx.
Since the integrand is a linear function, the function values f(xi) = 2xi + 3 remain constant throughout the interval. Therefore, the Trapezoidal Rule becomes exact, and the approximation becomes the exact value of the integral.
Conclusion:
The Trapezoidal Rule gives an exact value of the integral when the integrand is a linear function. This is because the Trapezoidal Rule accurately approximates the area under the curve by dividing it into trapezoids with equal widths. For linear functions, the heights of the trapezoids remain constant, resulting in an exact approximation of the integral.
The Trapezoidal Rule is a numerical integration method that approximates the definite integral of a function by dividing the area under the curve into trapezoids. This method is simple to implement and provides a good approximation for smooth functions.
Explanation:
The Trapezoidal Rule can give an exact value of the integral when the integrand is a linear function. In this case, the function can be represented by a straight line, and the area under the curve can be accurately calculated using the trapezoidal approximation.
Reasoning:
The Trapezoidal Rule approximates the area under the curve by dividing it into trapezoids. Each trapezoid is formed by connecting two adjacent points on the curve with a straight line segment. The area of each trapezoid is then calculated by taking the average of the heights of the two adjacent points and multiplying it by the width of the trapezoid.
When the integrand is a linear function, the curve is a straight line. In this case, the Trapezoidal Rule accurately approximates the area under the curve by dividing it into trapezoids with equal widths. Since the function is linear, the heights of the trapezoids remain constant throughout the interval, and the trapezoidal approximation becomes exact.
Example:
Let's consider the linear function f(x) = 2x + 3 over the interval [1, 5]. Using the Trapezoidal Rule, we divide the interval into n subintervals and approximate the integral as follows:
∫[1, 5] (2x + 3) dx ≈ Δx/2 * [f(x0) + 2f(x1) + 2f(x2) + ... + 2f(xn-1) + f(xn)]
where Δx = (b - a)/n is the width of each subinterval, x0 = 1, xn = 5, and xi = a + iΔx.
Since the integrand is a linear function, the function values f(xi) = 2xi + 3 remain constant throughout the interval. Therefore, the Trapezoidal Rule becomes exact, and the approximation becomes the exact value of the integral.
Conclusion:
The Trapezoidal Rule gives an exact value of the integral when the integrand is a linear function. This is because the Trapezoidal Rule accurately approximates the area under the curve by dividing it into trapezoids with equal widths. For linear functions, the heights of the trapezoids remain constant, resulting in an exact approximation of the integral.
Find f(2.75) using Newton’s Forward interpolation formula from the following table.

- a)1.8296875
- b)18.296875
- c)22.296875
- d)24.296875
Correct answer is option 'A'. Can you explain this answer?
Find f(2.75) using Newton’s Forward interpolation formula from the following table.


a)
1.8296875
b)
18.296875
c)
22.296875
d)
24.296875

|
Pioneer Academy answered |
Here,
x0 = 1.5
x = 2.75
h = 0.5
x = x0 + nh,
2.75 = 1.5 + n(0.5)
n = 2.5

y0 is 3.375 since it is forward interpolation formula.
Δy0 = 3.625
Δ2y0 = 3
Δ3y0 = 0.75
Δ4y0 = 0
Δ5y0 = 0
Substituting in the formula,
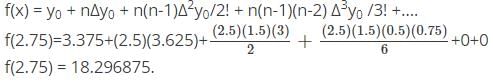
x0 = 1.5
x = 2.75
h = 0.5
x = x0 + nh,
2.75 = 1.5 + n(0.5)
n = 2.5

y0 is 3.375 since it is forward interpolation formula.
Δy0 = 3.625
Δ2y0 = 3
Δ3y0 = 0.75
Δ4y0 = 0
Δ5y0 = 0
Substituting in the formula,
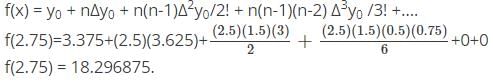
Which of the following is/are the problems in teaching and learning of mathematics?
I. Crude assessment
II. Lack of interest
III. Inadequate teacher preparation- a)I and III
- b)II and III
- c)I, II and III
- d)Only II
Correct answer is option 'C'. Can you explain this answer?
Which of the following is/are the problems in teaching and learning of mathematics?
I. Crude assessment
II. Lack of interest
III. Inadequate teacher preparation
I. Crude assessment
II. Lack of interest
III. Inadequate teacher preparation
a)
I and III
b)
II and III
c)
I, II and III
d)
Only II

|
Nabanita Saha answered |
The correct answer is option 'C' - I, II and III are all problems in teaching and learning of mathematics. Let's discuss each problem in detail:
I. Crude assessment:
- Crude assessment refers to the use of simplistic or insufficient methods to evaluate students' understanding and mastery of mathematical concepts.
- It can involve relying solely on written examinations that focus on rote memorization and procedural knowledge rather than deep understanding and problem-solving skills.
- This approach does not effectively capture the true extent of students' mathematical abilities and may lead to inaccurate assessments of their progress.
- Crude assessment can hinder students' motivation and engagement with mathematics, as they may perceive it as a repetitive and meaningless exercise.
II. Lack of interest:
- Many students develop a lack of interest in mathematics due to various factors, such as a perceived lack of relevance to their daily lives or negative experiences in the subject.
- When students are not interested in mathematics, they may struggle to engage with the content, leading to a lack of effort and motivation to learn.
- This lack of interest can hinder their ability to grasp new concepts, solve problems, and develop mathematical reasoning skills.
- Teachers need to employ engaging and interactive teaching methods, real-world applications, and relevant examples to spark students' interest in mathematics.
III. Inadequate teacher preparation:
- Teachers play a critical role in facilitating effective learning experiences for students.
- Inadequate preparation of teachers in terms of content knowledge, pedagogical strategies, and classroom management can significantly impact the teaching and learning of mathematics.
- Teachers need to have a deep understanding of mathematical concepts and be able to effectively communicate and explain them to students.
- They should also be familiar with various instructional strategies, problem-solving approaches, and assessment methods to cater to the diverse learning needs of students.
- Inadequately prepared teachers may struggle to deliver engaging and effective mathematics lessons, leading to students' disengagement and poor learning outcomes.
In conclusion, all three mentioned problems - crude assessment, lack of interest, and inadequate teacher preparation - contribute to the challenges faced in teaching and learning of mathematics. Addressing these problems requires a comprehensive approach that involves improved assessment methods, student-centered teaching practices, and enhanced teacher training and professional development.
I. Crude assessment:
- Crude assessment refers to the use of simplistic or insufficient methods to evaluate students' understanding and mastery of mathematical concepts.
- It can involve relying solely on written examinations that focus on rote memorization and procedural knowledge rather than deep understanding and problem-solving skills.
- This approach does not effectively capture the true extent of students' mathematical abilities and may lead to inaccurate assessments of their progress.
- Crude assessment can hinder students' motivation and engagement with mathematics, as they may perceive it as a repetitive and meaningless exercise.
II. Lack of interest:
- Many students develop a lack of interest in mathematics due to various factors, such as a perceived lack of relevance to their daily lives or negative experiences in the subject.
- When students are not interested in mathematics, they may struggle to engage with the content, leading to a lack of effort and motivation to learn.
- This lack of interest can hinder their ability to grasp new concepts, solve problems, and develop mathematical reasoning skills.
- Teachers need to employ engaging and interactive teaching methods, real-world applications, and relevant examples to spark students' interest in mathematics.
III. Inadequate teacher preparation:
- Teachers play a critical role in facilitating effective learning experiences for students.
- Inadequate preparation of teachers in terms of content knowledge, pedagogical strategies, and classroom management can significantly impact the teaching and learning of mathematics.
- Teachers need to have a deep understanding of mathematical concepts and be able to effectively communicate and explain them to students.
- They should also be familiar with various instructional strategies, problem-solving approaches, and assessment methods to cater to the diverse learning needs of students.
- Inadequately prepared teachers may struggle to deliver engaging and effective mathematics lessons, leading to students' disengagement and poor learning outcomes.
In conclusion, all three mentioned problems - crude assessment, lack of interest, and inadequate teacher preparation - contribute to the challenges faced in teaching and learning of mathematics. Addressing these problems requires a comprehensive approach that involves improved assessment methods, student-centered teaching practices, and enhanced teacher training and professional development.
In which of the following categories can we put Bisection method?- a)Bracket Solutions
- b)Graphical Solution
- c)Empirical Solutions
- d)Trial Solutions
Correct answer is option 'A'. Can you explain this answer?
In which of the following categories can we put Bisection method?
a)
Bracket Solutions
b)
Graphical Solution
c)
Empirical Solutions
d)
Trial Solutions
|
|
Sanya Agarwal answered |
Bracketing Methods:
- All bracketing methods always converge, whereas open methods (may sometimes diverge).
- We must start with an initial interval [a,b], where f(a) and f(b) have opposite signs.
- Since the graph y = f(x) of a continuous function is unbroken, it will cross the abscissa at a zero x = 'a' that lies somewhere within the interval [a,b].
- One of the ways to test a numerical method for solving the equation f(x) = 0 is to check its performance on a polynomial whose roots are known.
Bisection method:
Used to find the root for a function. Root of a function f(x) = a such that f(a)= 0
Property: if a function f(x) is continuous on the interval [a…b] and sign of f(a) ≠ sign of f(b). There is a value c belongs to [a…b] such that f(c) = 0, means c is a root in between [a….b]
Note:
Bisection method cut the interval into 2 halves and check which half contains a root of the equation.
1) Suppose interval [a, b] .
2) Cut interval in the middle to find m : m = (a + b)/2
3) sign of f(m) not matches with f(a), proceed the search in new interval.
Used to find the root for a function. Root of a function f(x) = a such that f(a)= 0
Property: if a function f(x) is continuous on the interval [a…b] and sign of f(a) ≠ sign of f(b). There is a value c belongs to [a…b] such that f(c) = 0, means c is a root in between [a….b]
Note:
Bisection method cut the interval into 2 halves and check which half contains a root of the equation.
1) Suppose interval [a, b] .
2) Cut interval in the middle to find m : m = (a + b)/2
3) sign of f(m) not matches with f(a), proceed the search in new interval.
How will you cater to the needs of visually challenged students of your classroom in an inclusive school?- a)Use alternate teaching-learning methods and resources.
- b)Send them to special educator.
- c)Provide them extra time for practice.
- d)Make them sit with high achievers
Correct answer is option 'A'. Can you explain this answer?
How will you cater to the needs of visually challenged students of your classroom in an inclusive school?
a)
Use alternate teaching-learning methods and resources.
b)
Send them to special educator.
c)
Provide them extra time for practice.
d)
Make them sit with high achievers

|
Mira Sharma answered |
Alternate Teaching-Learning Methods and Resources:
Using alternate teaching methods and resources is crucial for catering to the needs of visually challenged students in an inclusive school. This could include providing braille materials, audio books, tactile resources, and assistive technologies to ensure that these students can access the curriculum effectively.
Individualized Instruction:
It is important to provide individualized instruction to visually challenged students to meet their unique learning needs. This may involve adapting teaching strategies, providing additional support, and offering accommodations to help these students succeed in the classroom.
Collaboration with Special Educators:
While sending visually challenged students to special educators can be helpful, it is equally important for regular classroom teachers to collaborate with these professionals. By working together, teachers can develop effective strategies for supporting visually challenged students and promoting their academic success.
Creating an Inclusive Classroom Environment:
Inclusive schools should strive to create an environment where visually challenged students feel welcomed and supported. This involves promoting a culture of acceptance, understanding, and respect for diversity within the classroom.
Encouraging Peer Support:
Encouraging visually challenged students to sit with high achievers can be beneficial in fostering peer support. High achievers can serve as role models, mentors, and sources of inspiration for visually challenged students, helping them to feel included and motivated in the classroom.
In conclusion, catering to the needs of visually challenged students in an inclusive school requires a combination of alternate teaching methods, individualized instruction, collaboration with special educators, creating an inclusive environment, and encouraging peer support. By implementing these strategies, educators can ensure that visually challenged students receive the support and accommodations they need to thrive academically.
Using alternate teaching methods and resources is crucial for catering to the needs of visually challenged students in an inclusive school. This could include providing braille materials, audio books, tactile resources, and assistive technologies to ensure that these students can access the curriculum effectively.
Individualized Instruction:
It is important to provide individualized instruction to visually challenged students to meet their unique learning needs. This may involve adapting teaching strategies, providing additional support, and offering accommodations to help these students succeed in the classroom.
Collaboration with Special Educators:
While sending visually challenged students to special educators can be helpful, it is equally important for regular classroom teachers to collaborate with these professionals. By working together, teachers can develop effective strategies for supporting visually challenged students and promoting their academic success.
Creating an Inclusive Classroom Environment:
Inclusive schools should strive to create an environment where visually challenged students feel welcomed and supported. This involves promoting a culture of acceptance, understanding, and respect for diversity within the classroom.
Encouraging Peer Support:
Encouraging visually challenged students to sit with high achievers can be beneficial in fostering peer support. High achievers can serve as role models, mentors, and sources of inspiration for visually challenged students, helping them to feel included and motivated in the classroom.
In conclusion, catering to the needs of visually challenged students in an inclusive school requires a combination of alternate teaching methods, individualized instruction, collaboration with special educators, creating an inclusive environment, and encouraging peer support. By implementing these strategies, educators can ensure that visually challenged students receive the support and accommodations they need to thrive academically.
Calculate the volume of third section, if the areas are 76.32 sq. m and 24.56 sq. m with are at a distance of 4 m.- a)210.11 cu. m
- b)201.67 cu. m
- c)201.76 cu. m
- d)210.76 cu. m
Correct answer is option 'C'. Can you explain this answer?
Calculate the volume of third section, if the areas are 76.32 sq. m and 24.56 sq. m with are at a distance of 4 m.
a)
210.11 cu. m
b)
201.67 cu. m
c)
201.76 cu. m
d)
210.76 cu. m
|
|
Anjana Singh answered |
Volume of the third section of a prismoid can be calculated as,
V = d/2 (A3 + A4). On substitution, we get
V = 4/2 (76.32 + 24.56)
V = 201.76 cu. m.
V = d/2 (A3 + A4). On substitution, we get
V = 4/2 (76.32 + 24.56)
V = 201.76 cu. m.
Find the area of segment if the values of co-ordinates are given as 119.65m, 45.76m and 32.87m. They are placed at a distance of 2 m each.- a)20.43 sq. m
- b)2.34 sq. m
- c)20.34 sq. m
- d)87.34 sq. m
Correct answer is option 'C'. Can you explain this answer?
Find the area of segment if the values of co-ordinates are given as 119.65m, 45.76m and 32.87m. They are placed at a distance of 2 m each.
a)
20.43 sq. m
b)
2.34 sq. m
c)
20.34 sq. m
d)
87.34 sq. m
|
|
Anjana Singh answered |
The area of the segment can be found out by using,
A = (2/3)*(O1-(O0+O2/2)). On substitution, we get
A = (2/3)*(45.76-(119.65+32.87/2))
A = -20.34 Sq. m (negative sign has no significance)
A = 20.34 sq. m.
A = (2/3)*(O1-(O0+O2/2)). On substitution, we get
A = (2/3)*(45.76-(119.65+32.87/2))
A = -20.34 Sq. m (negative sign has no significance)
A = 20.34 sq. m.
If f(x) = x2, then the second order divided difference for the points x0, x1, x2 will be:- a)-1
- b)
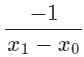
- c)1
- d)
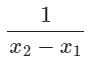
Correct answer is option 'C'. Can you explain this answer?
If f(x) = x2, then the second order divided difference for the points x0, x1, x2 will be:
a)
-1
b)
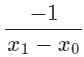
c)
1
d)
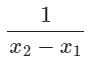

|
Pioneer Academy answered |
Concept:
If data points are given as a function of f, then the various order divided differences are as follows,
Zeroth-order divided difference:
f[x0] = f(x0);
First-order divided difference:
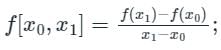
Second-order divided difference:
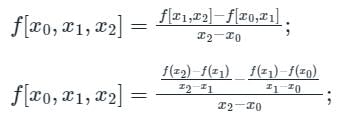
Calculation:
Given f(x) = x2;
Using the second-order divided difference formula, we get
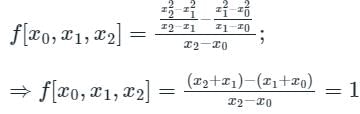
∴ the second-order divided difference of x2 is 1.
If data points are given as a function of f, then the various order divided differences are as follows,
Zeroth-order divided difference:
f[x0] = f(x0);
First-order divided difference:
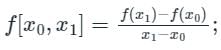
Second-order divided difference:
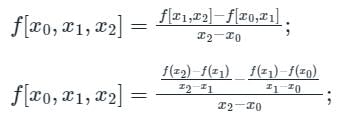
Calculation:
Given f(x) = x2;
Using the second-order divided difference formula, we get
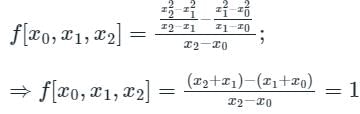
∴ the second-order divided difference of x2 is 1.
Which test is used to find errors committed by students during mathematical operations?- a)Diagnostic reading test
- b)Remedial test
- c)Diagnostic mathematical skill test
- d)Observation test
Correct answer is option 'C'. Can you explain this answer?
Which test is used to find errors committed by students during mathematical operations?
a)
Diagnostic reading test
b)
Remedial test
c)
Diagnostic mathematical skill test
d)
Observation test

|
Anmol Nair answered |
The correct answer is option 'C', the Diagnostic Mathematical Skill Test.
Explanation:
The Diagnostic Mathematical Skill Test is used to find errors committed by students during mathematical operations. This test is designed to assess the student's understanding and application of mathematical concepts and procedures. It helps identify specific areas where the student may be making mistakes or struggling with certain concepts.
The purpose of the Diagnostic Mathematical Skill Test is to diagnose the student's mathematical abilities and identify any gaps in their knowledge or understanding. It can help determine the specific areas that need improvement and provide insights into the student's strengths and weaknesses in mathematical operations.
By administering this test, educators can identify common errors or misconceptions made by students, such as calculation errors, incorrect application of formulas or procedures, misunderstanding of mathematical concepts, or lack of problem-solving skills. This information can be used to guide instruction and provide targeted remediation for individual students.
The Diagnostic Mathematical Skill Test typically includes a variety of mathematical problems that cover different topics and skills. It may include questions related to arithmetic operations (addition, subtraction, multiplication, division), fractions, decimals, percentages, algebraic equations, geometry, and more. The test may be administered in written or digital format, depending on the educational setting.
Overall, the Diagnostic Mathematical Skill Test is a valuable tool for educators to assess and address the specific errors and misconceptions made by students during mathematical operations. It helps identify areas for improvement and guides instruction to ensure students develop a strong foundation in mathematical skills.
Explanation:
The Diagnostic Mathematical Skill Test is used to find errors committed by students during mathematical operations. This test is designed to assess the student's understanding and application of mathematical concepts and procedures. It helps identify specific areas where the student may be making mistakes or struggling with certain concepts.
The purpose of the Diagnostic Mathematical Skill Test is to diagnose the student's mathematical abilities and identify any gaps in their knowledge or understanding. It can help determine the specific areas that need improvement and provide insights into the student's strengths and weaknesses in mathematical operations.
By administering this test, educators can identify common errors or misconceptions made by students, such as calculation errors, incorrect application of formulas or procedures, misunderstanding of mathematical concepts, or lack of problem-solving skills. This information can be used to guide instruction and provide targeted remediation for individual students.
The Diagnostic Mathematical Skill Test typically includes a variety of mathematical problems that cover different topics and skills. It may include questions related to arithmetic operations (addition, subtraction, multiplication, division), fractions, decimals, percentages, algebraic equations, geometry, and more. The test may be administered in written or digital format, depending on the educational setting.
Overall, the Diagnostic Mathematical Skill Test is a valuable tool for educators to assess and address the specific errors and misconceptions made by students during mathematical operations. It helps identify areas for improvement and guides instruction to ensure students develop a strong foundation in mathematical skills.
The value of y’/x’ in terms of the angle 0 is given by ______- a)tanθ
- b)secθ
- c)cotθ
- d)cosecθ
Correct answer is option 'A'. Can you explain this answer?
The value of y’/x’ in terms of the angle 0 is given by ______
a)
tanθ
b)
secθ
c)
cotθ
d)
cosecθ
|
|
Anjana Singh answered |
The value of derivative of a function f(x) is given as f’(x) = y’/x’. In terms of theta tangent is the ration of opposite side to adjacent side hence y’/x’ = tanθ.
Which of the following indicates the assumption assumed in the trapezoidal formula?- a)mid-area is the mean of the starting area
- b)mid-area is the mean of the end area
- c)mid-area is the mean
- d)mid-area is not the mean of the end area
Correct answer is option 'B'. Can you explain this answer?
Which of the following indicates the assumption assumed in the trapezoidal formula?
a)
mid-area is the mean of the starting area
b)
mid-area is the mean of the end area
c)
mid-area is the mean
d)
mid-area is not the mean of the end area

|
Sparsh Unni answered |
Understanding the Trapezoidal Formula
The trapezoidal rule is a numerical method for approximating the definite integral of a function. It is particularly useful in civil engineering for calculating areas under curves. The assumption in the trapezoidal formula is crucial for its application.
Key Assumption in the Trapezoidal Formula
- The trapezoidal rule assumes that the function being evaluated is linear between the two endpoints of the interval.
- This means that the area of the trapezoid formed by connecting the endpoints of the function at the interval can be accurately represented.
Why Option B is Correct
- Option B states: "mid-area is the mean of the end area." This is accurate because the trapezoidal rule estimates the area under the curve by averaging the function values at the two endpoints.
- The formula for the trapezoidal rule is:
\[
\text{Area} \approx \frac{(b-a)}{2} \times [f(a) + f(b)]
\]
where \(f(a)\) and \(f(b)\) are the values of the function at the endpoints \(a\) and \(b\).
- The assumption is that the average of these two function values (the heights of the trapezoid) represents the mid-area correctly, making it reasonable to take the average of the end areas.
Implications of the Assumption
- If the function is not linear, the trapezoidal rule may lead to underestimation or overestimation of the actual area.
- Understanding this assumption helps engineers apply the trapezoidal rule more effectively in real-world scenarios, ensuring more accurate calculations in project designs and assessments.
This detailed understanding of the trapezoidal formula and its assumptions enhances the reliability of numerical integration in civil engineering applications.
The trapezoidal rule is a numerical method for approximating the definite integral of a function. It is particularly useful in civil engineering for calculating areas under curves. The assumption in the trapezoidal formula is crucial for its application.
Key Assumption in the Trapezoidal Formula
- The trapezoidal rule assumes that the function being evaluated is linear between the two endpoints of the interval.
- This means that the area of the trapezoid formed by connecting the endpoints of the function at the interval can be accurately represented.
Why Option B is Correct
- Option B states: "mid-area is the mean of the end area." This is accurate because the trapezoidal rule estimates the area under the curve by averaging the function values at the two endpoints.
- The formula for the trapezoidal rule is:
\[
\text{Area} \approx \frac{(b-a)}{2} \times [f(a) + f(b)]
\]
where \(f(a)\) and \(f(b)\) are the values of the function at the endpoints \(a\) and \(b\).
- The assumption is that the average of these two function values (the heights of the trapezoid) represents the mid-area correctly, making it reasonable to take the average of the end areas.
Implications of the Assumption
- If the function is not linear, the trapezoidal rule may lead to underestimation or overestimation of the actual area.
- Understanding this assumption helps engineers apply the trapezoidal rule more effectively in real-world scenarios, ensuring more accurate calculations in project designs and assessments.
This detailed understanding of the trapezoidal formula and its assumptions enhances the reliability of numerical integration in civil engineering applications.
If f(0) = 3, f(1) = 5, f(3) = 21, then the unique polynomial of degree 2 or less using Newton divided difference interpolation will be:- a)2x2 + 2x + 1
- b)2x2 - 3x + 1
- c)2x2 + 3
- d)x2 + 3x - 2
Correct answer is option 'C'. Can you explain this answer?
If f(0) = 3, f(1) = 5, f(3) = 21, then the unique polynomial of degree 2 or less using Newton divided difference interpolation will be:
a)
2x2 + 2x + 1
b)
2x2 - 3x + 1
c)
2x2 + 3
d)
x2 + 3x - 2
|
|
Sanya Agarwal answered |
Concept:
Newton’s divided difference polynomial method:
Second order polynomial interpolation using Newton’s divided difference polynomial method is as follows,
Given (x0,y0), (x1,y1), (x2,y2) be the data points and f(x) be the quadratic interpolant, then f(x) is given by
f(x) = b0 + b1(x – x0) + b2 (x – x0)(x – x1);
Where
b0 = f(x0);

Calculation:
Given f(0) = 3, f(1) = 5, f(3) = 21;
⇒ (0,3), (1,5), (3,21) are the data points;
The polynomial will be f(x) = b0 + b1(x) + b2 (x)(x – 1);
⇒ b0 = f(0) = 3;
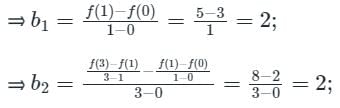
Substituting the constant b0, b1, b2 in the quadratic interpolant,
⇒ f(x) = 3 + 2x + 2 (x)(x – 1) = 3 + 2x + 2x2 – 2x = 3 + 2x2;
The unique polynomial of degree 2 will be f(x) = 3 + 2x2;
Easy method:
To save time, simply substitute the data points in the polynomials given in options and find the polynomial that is satisfying all data points.
Newton’s divided difference polynomial method:
Second order polynomial interpolation using Newton’s divided difference polynomial method is as follows,
Given (x0,y0), (x1,y1), (x2,y2) be the data points and f(x) be the quadratic interpolant, then f(x) is given by
f(x) = b0 + b1(x – x0) + b2 (x – x0)(x – x1);
Where
b0 = f(x0);

Calculation:
Given f(0) = 3, f(1) = 5, f(3) = 21;
⇒ (0,3), (1,5), (3,21) are the data points;
The polynomial will be f(x) = b0 + b1(x) + b2 (x)(x – 1);
⇒ b0 = f(0) = 3;
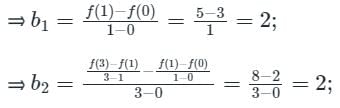
Substituting the constant b0, b1, b2 in the quadratic interpolant,
⇒ f(x) = 3 + 2x + 2 (x)(x – 1) = 3 + 2x + 2x2 – 2x = 3 + 2x2;
The unique polynomial of degree 2 will be f(x) = 3 + 2x2;
Easy method:
To save time, simply substitute the data points in the polynomials given in options and find the polynomial that is satisfying all data points.
The parameter E which we use for least square method is called as ______- a)Sum of residues
- b)Residues
- c)Error
- d)Sum of errors
Correct answer is option 'A'. Can you explain this answer?
The parameter E which we use for least square method is called as ______
a)
Sum of residues
b)
Residues
c)
Error
d)
Sum of errors

|
Pranab Chaudhary answered |
Understanding the Least Squares Method
The least squares method is a statistical technique used to minimize the sum of the squares of the residuals, which are the differences between observed and predicted values. In this context, the parameter \( E \) is crucial.
Definition of Residues
- **Residues** are defined as the differences between the observed values (\( y_i \)) and the values predicted by the model (\( \hat{y}_i \)).
- Mathematically, it is expressed as:
\[
r_i = y_i - \hat{y}_i
\]
Sum of Residues
- The term **Sum of Residues** refers to the cumulative sum of these individual residues. However, in least squares, we are concerned with the square of these residues.
Why Option 'A' is Correct
- The parameter \( E \) specifically represents the **Sum of Squares of Residues**, which is calculated as:
\[
E = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2
\]
- This minimization of \( E \) leads to the best-fitting line or curve for the given data points.
Importance in Civil Engineering
- In civil engineering, accurate predictions and models are essential for design and analysis. The least squares method provides a robust way to achieve these predictions by minimizing the discrepancies between observed and predicted values.
Conclusion
- Therefore, the correct answer is option 'A', as it accurately denotes the **Sum of Residues**, which is central to the least squares method.
The least squares method is a statistical technique used to minimize the sum of the squares of the residuals, which are the differences between observed and predicted values. In this context, the parameter \( E \) is crucial.
Definition of Residues
- **Residues** are defined as the differences between the observed values (\( y_i \)) and the values predicted by the model (\( \hat{y}_i \)).
- Mathematically, it is expressed as:
\[
r_i = y_i - \hat{y}_i
\]
Sum of Residues
- The term **Sum of Residues** refers to the cumulative sum of these individual residues. However, in least squares, we are concerned with the square of these residues.
Why Option 'A' is Correct
- The parameter \( E \) specifically represents the **Sum of Squares of Residues**, which is calculated as:
\[
E = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2
\]
- This minimization of \( E \) leads to the best-fitting line or curve for the given data points.
Importance in Civil Engineering
- In civil engineering, accurate predictions and models are essential for design and analysis. The least squares method provides a robust way to achieve these predictions by minimizing the discrepancies between observed and predicted values.
Conclusion
- Therefore, the correct answer is option 'A', as it accurately denotes the **Sum of Residues**, which is central to the least squares method.
Find the area of the traverse using Simpson’s rule if d= 12 m and the values of ordinates are 2.25m, 1.46m, 3.23m, 4.46m.- a)116.88 sq. m
- b)161.88 sq. m
- c)611.88 sq. m
- d)169.54 sq. m
Correct answer is option 'B'. Can you explain this answer?
Find the area of the traverse using Simpson’s rule if d= 12 m and the values of ordinates are 2.25m, 1.46m, 3.23m, 4.46m.
a)
116.88 sq. m
b)
161.88 sq. m
c)
611.88 sq. m
d)
169.54 sq. m
|
|
Anjana Singh answered |
The formula for Simpson’s rule can be given as Δ = (d/3)*((O0+O4) + 4*(O1+O3) + 2*(O2+O4)). On substitution, we get
Δ = (12/3)* ((2.25+4.46) + 4*(2.25+3.23) + 2*(1.46+4.46))
Δ = 161.88 sq. m.
Δ = (12/3)* ((2.25+4.46) + 4*(2.25+3.23) + 2*(1.46+4.46))
Δ = 161.88 sq. m.
The order of convergence of Newton Raphson method is- a)2
- b)3
- c)0
- d)1
Correct answer is option 'A'. Can you explain this answer?
The order of convergence of Newton Raphson method is
a)
2
b)
3
c)
0
d)
1

|
Sanskriti Datta answered |
Order of Convergence of Newton Raphson Method
The Newton Raphson method is an iterative numerical method used to find the roots of a given equation. It is a popular method due to its fast convergence rate. The order of convergence of the Newton Raphson method determines how quickly the method converges to the root.
The order of convergence can be defined as the rate at which the error in the approximate solution decreases as the number of iterations increases. In other words, it measures how fast the method converges to the root.
Explanation:
The order of convergence of the Newton Raphson method is determined by the behavior of the error term in the method. The error term is given by the difference between the current approximation and the true root of the equation.
In general, the order of convergence of the Newton Raphson method is 2. This means that the error term decreases quadratically as the number of iterations increases. The error at each iteration is roughly squared compared to the previous iteration.
However, there are cases where the order of convergence can be different. This occurs when the derivative of the function becomes zero or when the derivative changes sign near the root. In such cases, the order of convergence can be reduced.
Example:
Let's consider an example to illustrate the order of convergence of the Newton Raphson method. Suppose we want to find the root of the equation f(x) = x^2 - 4.
1. Initialize the initial guess x0 = 3.
2. Calculate the derivative of the function f'(x) = 2x.
3. Update the approximation using the Newton Raphson formula: x1 = x0 - f(x0)/f'(x0).
4. Repeat the process until the desired accuracy is achieved.
After a few iterations, we can observe that the error term decreases quadratically. The error at each iteration is roughly the square of the previous error, indicating a second-order convergence.
Hence, the correct answer is option 'A' - 2. The order of convergence of the Newton Raphson method is 2.
The Newton Raphson method is an iterative numerical method used to find the roots of a given equation. It is a popular method due to its fast convergence rate. The order of convergence of the Newton Raphson method determines how quickly the method converges to the root.
The order of convergence can be defined as the rate at which the error in the approximate solution decreases as the number of iterations increases. In other words, it measures how fast the method converges to the root.
Explanation:
The order of convergence of the Newton Raphson method is determined by the behavior of the error term in the method. The error term is given by the difference between the current approximation and the true root of the equation.
In general, the order of convergence of the Newton Raphson method is 2. This means that the error term decreases quadratically as the number of iterations increases. The error at each iteration is roughly squared compared to the previous iteration.
However, there are cases where the order of convergence can be different. This occurs when the derivative of the function becomes zero or when the derivative changes sign near the root. In such cases, the order of convergence can be reduced.
Example:
Let's consider an example to illustrate the order of convergence of the Newton Raphson method. Suppose we want to find the root of the equation f(x) = x^2 - 4.
1. Initialize the initial guess x0 = 3.
2. Calculate the derivative of the function f'(x) = 2x.
3. Update the approximation using the Newton Raphson formula: x1 = x0 - f(x0)/f'(x0).
4. Repeat the process until the desired accuracy is achieved.
After a few iterations, we can observe that the error term decreases quadratically. The error at each iteration is roughly the square of the previous error, indicating a second-order convergence.
Hence, the correct answer is option 'A' - 2. The order of convergence of the Newton Raphson method is 2.
Find n if x0 = 0.75825, x = 0.759 and h = 0.00005.- a)1.5
- b)15
- c)2.5
- d)25
Correct answer is option 'B'. Can you explain this answer?
Find n if x0 = 0.75825, x = 0.759 and h = 0.00005.
a)
1.5
b)
15
c)
2.5
d)
25

|
Anshu Kumar answered |
Given values:
x0 = 0.75825
x = 0.759
h = 0.00005
Formula for calculating n:
n = (x - x0) / h
Calculation:
n = (0.759 - 0.75825) / 0.00005
n = 0.00075 / 0.00005
n = 15
Therefore, the value of n is 15. Hence, the correct answer is option 'B' (15).
x0 = 0.75825
x = 0.759
h = 0.00005
Formula for calculating n:
n = (x - x0) / h
Calculation:
n = (0.759 - 0.75825) / 0.00005
n = 0.00075 / 0.00005
n = 15
Therefore, the value of n is 15. Hence, the correct answer is option 'B' (15).
Which order of Polynomials can best be integrated using Trapezoidal Rules?- a)3rd order
- b)4th order
- c)2nd order
- d)1st order
Correct answer is option 'D'. Can you explain this answer?
Which order of Polynomials can best be integrated using Trapezoidal Rules?
a)
3rd order
b)
4th order
c)
2nd order
d)
1st order
|
|
Anjana Singh answered |
The following table shows the different methods of numerical integration and degree of polynomials for which they will produce results of minimum error or zero error:

From the above table, it is clear that both Trapezoidal Rule polynomials of degree ≤ 1

From the above table, it is clear that both Trapezoidal Rule polynomials of degree ≤ 1
A student was asked to read the following numbers:
306, 406, 408, 4020
He reads as follows:
Thirty six, forty six, forty eight, forty twenty
The reason for error in reading is that- a)the student does not like maths class and finds the class boring
- b)the student has understood the concept of place value and its use also
- c)the student is not fit for study of maths
- d)the student is not able to understand the concept of place value and feels comfortable using two-digit numbers only
Correct answer is option 'D'. Can you explain this answer?
A student was asked to read the following numbers:
306, 406, 408, 4020
He reads as follows:
Thirty six, forty six, forty eight, forty twenty
The reason for error in reading is that
306, 406, 408, 4020
He reads as follows:
Thirty six, forty six, forty eight, forty twenty
The reason for error in reading is that
a)
the student does not like maths class and finds the class boring
b)
the student has understood the concept of place value and its use also
c)
the student is not fit for study of maths
d)
the student is not able to understand the concept of place value and feels comfortable using two-digit numbers only
|
|
Sanvi Kapoor answered |
Mathematics includes complex calculations, the study of patterns, shapes, and various geometrical figures. To develop a liking towards mathematics, the teacher should need to use innovative ideas to teach abstractions of mathematics.
- The manipulative tools are used in the teaching of mathematics to clear the complex and abstract mathematical concepts and to arouse the interest of students while learning mathematics.
Key Points
- Children often start learning numbers and counting even before entering school.
- They are made familiar with rhymes that teach the numbers while playing. The children imitate them and try to speak the numbers verbally.
- At the primary level, the children usually get confused in recognizing the face value and place value of the digits.
- For them, there is no difference between 004 and 400, as they do not understand that the position of a digit determines its place value. They may think that the ‘4’ in 46 represents 4, not 40.
- Instead of teaching the concept of place value using questions given in the textbook only, the teacher should involve the students in play activities that are relatable to real-world and are focused on the concept of place value i.e., use of money in daily life (10 represents 10 rupees whereas 1 represents only 1 rupee coin and 100 on a banknote denotes 100 rupees).
- This will compel students to think that a specific position of a number says a lot about its position that is its place value.
- The teacher can also use manipulative tools such as base ten blocks to teach the concept of place value to clear their ambivalent thoughts about place value.
- Base ten blocks are also known as the multi-base arithmetic blocks (MAB).
- These are basically used to teach basic mathematical concepts such as addition, subtraction, numbers, counting, and place value.
- They are made up of wood or plastic and comes in different sizes to show place value.
- The single wooden unit used to show the digits at ones place, the tens (having one rod divided into 10 parts) used to show digits at the tens place, and the flat surface of wood which is divided into 10× 10 used to show the digit at hundreds places.
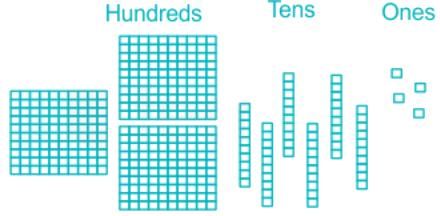
- In the above image, there are 4 single wooden units shown in the ones box, so here we have 4 ones. And 6 rods at tens, so 6 tens 6×10 means 60 and 3 flats of 100 i.e., 3×100 =300. By adding all these, 300+60+4 we will get 364.
- Such kind of manipulative tools can be very helpful in teaching effectively at the primary level and also keep the students engaged in the learning process.
Hence, could be concluded The reason for the error in reading is that the student is not able to understand the concept of place value and feels comfortable using two-digit numbers only because the student is reading only on the basis of face value, so the student needs the concept of place value.
When asked to write 44, some students of grade II wrote it as 404. As a teacher, how will you address this?- a)correct their answer in their copies
- b)explain principle of exchange using concrete material
- c)group them with those who have done it correctly
- d)tell them to find out correct answer
Correct answer is option 'B'. Can you explain this answer?
When asked to write 44, some students of grade II wrote it as 404. As a teacher, how will you address this?
a)
correct their answer in their copies
b)
explain principle of exchange using concrete material
c)
group them with those who have done it correctly
d)
tell them to find out correct answer
|
|
Sanvi Kapoor answered |
Concrete reasoning involves the ability to analyze information and solve problems on a literal ("concrete") level. We use concrete materials when we think through and solve hands-on problems. Explaining concepts through concrete materials helps in:
- Understanding of basic cause and effect relationships.
- Basic knowledge of names of objects, places, and people.
- To give the knowledge of the grouping concepts i.e. dividing 44 children into 2 equal groups and then demonstrating the children into diving the students of the class into 2 groups of 22 each. This is how we use concrete material which is helpful in determining the difference between 44 and 404 for children.
- Solving problems that do not involve theory, metaphor, or complex analogy.
Therefore, when students write 44 as 404 as a teacher, we will address this by explaining the principle of exchange using concrete materials.
Find f(5) using Newton’s Forward interpolation formula from the following table.

- a)71.109375
- b)61.103975
- c)70.103957
- d)71.103957
Correct answer is option 'A'. Can you explain this answer?
Find f(5) using Newton’s Forward interpolation formula from the following table.


a)
71.109375
b)
61.103975
c)
70.103957
d)
71.103957
|
|
Anjana Singh answered |
Here,
x0 = 0
x = 5
h = 2
x = x0 + nh,
5 = 0 + n(2)
n = 2.5
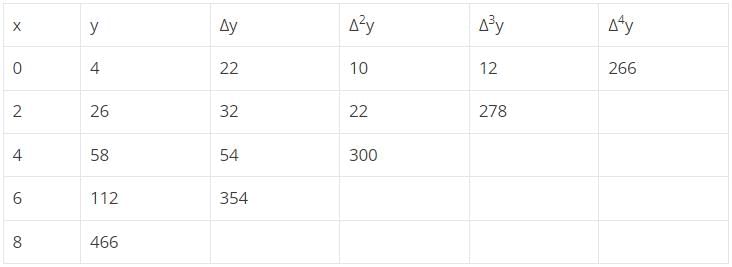
y0 is 4 since it is forward interpolation formula.
Δy0 = 22
Δ2y0 = 10
Δ3y0 = 12
Δ4y0 = 266
Substituting in the formula,
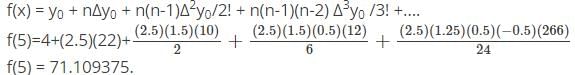
x0 = 0
x = 5
h = 2
x = x0 + nh,
5 = 0 + n(2)
n = 2.5

y0 is 4 since it is forward interpolation formula.
Δy0 = 22
Δ2y0 = 10
Δ3y0 = 12
Δ4y0 = 266
Substituting in the formula,
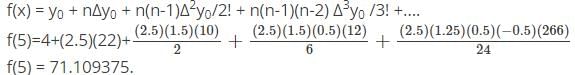
The real root of x3 + x2 + 3x + 4 = 0 correct to four decimal places, obtained using Newton Raphson method is- a)-1.3334
- b)1.3221
- c)-1.2229
- d)1.2929
Correct answer is option 'C'. Can you explain this answer?
The real root of x3 + x2 + 3x + 4 = 0 correct to four decimal places, obtained using Newton Raphson method is
a)
-1.3334
b)
1.3221
c)
-1.2229
d)
1.2929
|
|
Sanvi Kapoor answered |
Concept:
Newton-Raphson Method:
The iteration formula is given by
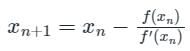
Where x0 is the initial value/root of the equation f(x) = 0
Given,
f(x) = x3 + x2 + 3x + 4 = 0
f'(x) = 3x2 + 2x + 3
∴ f(-1) = 1 > 0 and f(-2) = -6 < 0
∴ f(-1).f(-2) < 0
⇒ ∃ a root lies in [-1, -2]
Let, x0 = -1
By Newton Raphson method
First approximation
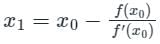

x1 = -1.25
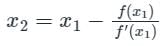
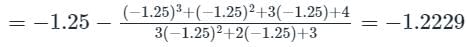
Newton-Raphson Method:
The iteration formula is given by
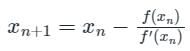
Where x0 is the initial value/root of the equation f(x) = 0
Given,
f(x) = x3 + x2 + 3x + 4 = 0
f'(x) = 3x2 + 2x + 3
∴ f(-1) = 1 > 0 and f(-2) = -6 < 0
∴ f(-1).f(-2) < 0
⇒ ∃ a root lies in [-1, -2]
Let, x0 = -1
By Newton Raphson method
First approximation
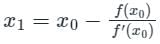

x1 = -1.25
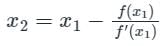
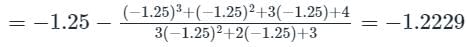
Find n for the following data if f(1.8) is asked.

- a)2.4
- b)3.4
- c)2.6
- d)3.6
Correct answer is option 'D'. Can you explain this answer?
Find n for the following data if f(1.8) is asked.


a)
2.4
b)
3.4
c)
2.6
d)
3.6
|
|
Anjana Singh answered |
Here, x0 is 0, h is 0.5, x is 1.8.
Substituting the values in the formula
x = x0 + nh,
1.8 = 0 + n(0.5)
n = 3.6.
Substituting the values in the formula
x = x0 + nh,
1.8 = 0 + n(0.5)
n = 3.6.
In which of the following cases, Simpson’s rule is adopted?- a)When straights are perpendicular
- b)When straights are parallel
- c)When straights form curves
- d)When straights form parabolic arcs
Correct answer is option 'B'. Can you explain this answer?
In which of the following cases, Simpson’s rule is adopted?
a)
When straights are perpendicular
b)
When straights are parallel
c)
When straights form curves
d)
When straights form parabolic arcs
|
|
Anjana Singh answered |
Even though Simpson’s rule assumes that short lengths of boundary between the ordinates are parabolic arcs, this method is more accurate for the case when straights act as a parallel to each other.
Find the polynomial for the following data.

- a)
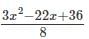
- b)3x2-22x+36
- c)

- d)
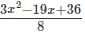
Correct answer is option 'A'. Can you explain this answer?
Find the polynomial for the following data.


a)
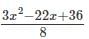
b)
3x2-22x+36
c)

d)
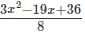
|
|
Anjana Singh answered |
Here,
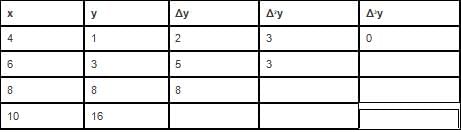
y0 is 1 since it is forward interpolation formula.
Δy0 = 2
Δ2y0 = 3
Δ3y0 = 0
x = x0 + nh,
x = 4 + n(2)
Hence
n = (x-4)/2
Substituting these values in the formula,
f(x) = y0 + nΔy0 + n(n-1)Δ2y0/2! + n(n-1)(n-2) Δ3y0 /3!,


y0 is 1 since it is forward interpolation formula.
Δy0 = 2
Δ2y0 = 3
Δ3y0 = 0
x = x0 + nh,
x = 4 + n(2)
Hence
n = (x-4)/2
Substituting these values in the formula,
f(x) = y0 + nΔy0 + n(n-1)Δ2y0/2! + n(n-1)(n-2) Δ3y0 /3!,

The iteration formula to find the reciprocal of a given number N by Newton’s method is- a)
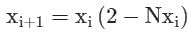
- b)
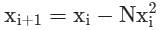
- c)
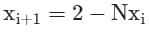
- d)
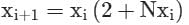
Correct answer is option 'A'. Can you explain this answer?
The iteration formula to find the reciprocal of a given number N by Newton’s method is
a)
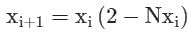
b)
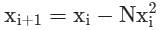
c)
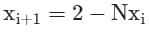
d)
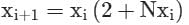
|
|
Sanya Agarwal answered |
Concept:
Newton-Raphson method: It has order of convergence 2 and number of guesses required is 1.
Iteration formula,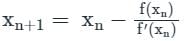
Calculation:
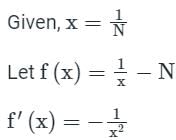
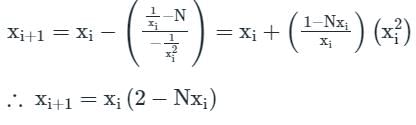
Newton-Raphson method: It has order of convergence 2 and number of guesses required is 1.
Iteration formula,
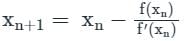
Calculation:
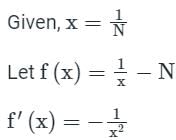
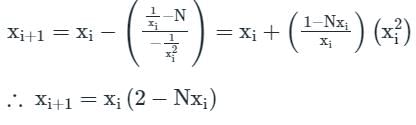
The equation f(x) is given as x2-4=0. Considering the initial approximation at x = 6 then the value of x1 is given as ____________- a)10/3
- b)4/3
- c)7/3
- d)13/3
Correct answer is option 'A'. Can you explain this answer?
The equation f(x) is given as x2-4=0. Considering the initial approximation at x = 6 then the value of x1 is given as ____________
a)
10/3
b)
4/3
c)
7/3
d)
13/3

|
Rutuja Pillai answered |
Solution:
To find the value of x1, we need to use the Newton-Raphson method, which is an iterative method for finding the roots of a function.
Step 1: Define the function
The given equation is f(x) = x^2 - 4.
Step 2: Find the derivative of the function
To use the Newton-Raphson method, we need to find the derivative of the function. In this case, the derivative of f(x) = x^2 - 4 is f'(x) = 2x.
Step 3: Perform the iteration
Using the initial approximation x = 6, we can perform the iteration to find the value of x1.
The Newton-Raphson iteration formula is given by:
x1 = x0 - f(x0)/f'(x0)
where x0 is the initial approximation.
Substituting the values into the formula, we have:
x1 = 6 - (6^2 - 4)/(2*6)
= 6 - (36 - 4)/12
= 6 - 32/12
= 6 - 8/3
= 18/3 - 8/3
= 10/3
Therefore, the value of x1 is 10/3.
Final Answer
The correct answer is option A) 10/3.
The approximate value of a root of x3 – 13 = 0, then 3.5 as initial value, after one iteration using Newton-Raphson method, is - a)2.687
- b)2.678
- c)3.607
- d)3.597
Correct answer is option 'A'. Can you explain this answer?
The approximate value of a root of x3 – 13 = 0, then 3.5 as initial value, after one iteration using Newton-Raphson method, is
a)
2.687
b)
2.678
c)
3.607
d)
3.597

|
Raghavendra Goyal answered |
The value of a root of x^3 can vary depending on the specific equation or context. Without more information, it is not possible to determine an approximate value.
Let f(x) = x2 - 2x + 2 be a continuous function defined on x ∈ [1, 3]. The point x at which the tangent of f(x) becomes parallel to the straight line joining f(1) and f(3) is- a)3
- b)0
- c)2
- d)1
Correct answer is option 'C'. Can you explain this answer?
Let f(x) = x2 - 2x + 2 be a continuous function defined on x ∈ [1, 3]. The point x at which the tangent of f(x) becomes parallel to the straight line joining f(1) and f(3) is
a)
3
b)
0
c)
2
d)
1
|
|
Anjana Singh answered |
Concept:
By lagrangian mean value theorem,
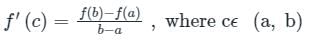
Calculation:
Given:
f(x) = x2 – 2x + 2, x ϵ [1, 3]
By lagrangian mean value theorem
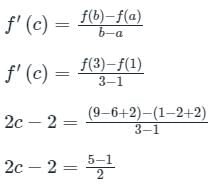
c = 2
By lagrangian mean value theorem,
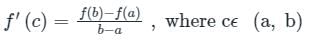
Calculation:
Given:
f(x) = x2 – 2x + 2, x ϵ [1, 3]
By lagrangian mean value theorem
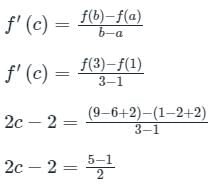
c = 2
The results obtained are greater than which among the following?- a)Prismoidal rule
- b)Trapezoidal rule
- c)Rectangular rule
- d)Square rule
Correct answer is option 'B'. Can you explain this answer?
The results obtained are greater than which among the following?
a)
Prismoidal rule
b)
Trapezoidal rule
c)
Rectangular rule
d)
Square rule

|
Parth Patel answered |
Introduction
The question is asking which among the given methods (Prismoidal rule, Trapezoidal rule, Rectangular rule, and Square rule) yields results that are less than the others.
Explanation
To determine the answer, let's briefly discuss each method and compare their accuracy.
1. Prismoidal Rule
The prismoidal rule is a numerical integration method used to calculate the volume of irregular solids. It divides the solid into a series of prisms with trapezoidal cross-sections. The volume of each prism is then calculated using the trapezoidal rule and summed to obtain the total volume. The prismoidal rule provides a more accurate result than the trapezoidal rule.
2. Trapezoidal Rule
The trapezoidal rule is a simple numerical integration method that approximates the area under a curve by dividing it into trapezoids. It assumes a linear interpolation between the data points and sums the areas of the trapezoids to estimate the total area. The trapezoidal rule provides a less accurate result compared to more advanced methods like the prismoidal rule.
3. Rectangular Rule
The rectangular rule, also known as the midpoint rule, is another numerical integration method that approximates the area under a curve. It divides the area into a series of rectangles, with the height of each rectangle determined by the function value at the midpoint of the interval. The rectangular rule provides a less accurate result compared to the trapezoidal rule.
4. Square Rule
The square rule is not a well-known numerical integration method. It is not commonly used in engineering calculations and is not as accurate as the other methods mentioned above.
Conclusion
Comparing the accuracy of the methods, the trapezoidal rule provides less accurate results than the prismoidal rule. Therefore, the correct answer is option 'B' - the results obtained using the trapezoidal rule are greater than those obtained using the other methods mentioned.
The question is asking which among the given methods (Prismoidal rule, Trapezoidal rule, Rectangular rule, and Square rule) yields results that are less than the others.
Explanation
To determine the answer, let's briefly discuss each method and compare their accuracy.
1. Prismoidal Rule
The prismoidal rule is a numerical integration method used to calculate the volume of irregular solids. It divides the solid into a series of prisms with trapezoidal cross-sections. The volume of each prism is then calculated using the trapezoidal rule and summed to obtain the total volume. The prismoidal rule provides a more accurate result than the trapezoidal rule.
2. Trapezoidal Rule
The trapezoidal rule is a simple numerical integration method that approximates the area under a curve by dividing it into trapezoids. It assumes a linear interpolation between the data points and sums the areas of the trapezoids to estimate the total area. The trapezoidal rule provides a less accurate result compared to more advanced methods like the prismoidal rule.
3. Rectangular Rule
The rectangular rule, also known as the midpoint rule, is another numerical integration method that approximates the area under a curve. It divides the area into a series of rectangles, with the height of each rectangle determined by the function value at the midpoint of the interval. The rectangular rule provides a less accurate result compared to the trapezoidal rule.
4. Square Rule
The square rule is not a well-known numerical integration method. It is not commonly used in engineering calculations and is not as accurate as the other methods mentioned above.
Conclusion
Comparing the accuracy of the methods, the trapezoidal rule provides less accurate results than the prismoidal rule. Therefore, the correct answer is option 'B' - the results obtained using the trapezoidal rule are greater than those obtained using the other methods mentioned.
Trapezoidal formula is also known as _____- a)Simpson’s rule
- b)Co-ordinate method
- c)Prismoidal method
- d)Average end area method
Correct answer is option 'D'. Can you explain this answer?
Trapezoidal formula is also known as _____
a)
Simpson’s rule
b)
Co-ordinate method
c)
Prismoidal method
d)
Average end area method
|
|
Anjana Singh answered |
This method is based on the assumption that the mid-area is the mean of the end areas, which make it the Average end area method.
Consider the definite integral  Let Ie be the exact value of the integral. If the same integral is estimated using Simpson’s rule with 10 equal subintervals, the value is Is. The percentage error is defined as e = 100 × (Ie - Is)/Ie The value of e is
Let Ie be the exact value of the integral. If the same integral is estimated using Simpson’s rule with 10 equal subintervals, the value is Is. The percentage error is defined as e = 100 × (Ie - Is)/Ie The value of e is- a)2.5
- b)3.5
- c)1.2
- d)0
Correct answer is option 'D'. Can you explain this answer?
Consider the definite integral  Let Ie be the exact value of the integral. If the same integral is estimated using Simpson’s rule with 10 equal subintervals, the value is Is. The percentage error is defined as e = 100 × (Ie - Is)/Ie The value of e is
Let Ie be the exact value of the integral. If the same integral is estimated using Simpson’s rule with 10 equal subintervals, the value is Is. The percentage error is defined as e = 100 × (Ie - Is)/Ie The value of e is
 Let Ie be the exact value of the integral. If the same integral is estimated using Simpson’s rule with 10 equal subintervals, the value is Is. The percentage error is defined as e = 100 × (Ie - Is)/Ie The value of e is
Let Ie be the exact value of the integral. If the same integral is estimated using Simpson’s rule with 10 equal subintervals, the value is Is. The percentage error is defined as e = 100 × (Ie - Is)/Ie The value of e isa)
2.5
b)
3.5
c)
1.2
d)
0
|
|
Anjana Singh answered |
Simpson's rule is given by -
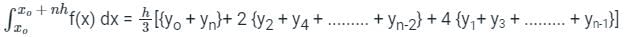
h = width of interval / step length
yo, y1 ........ yn - ordinates corresponding to xo, x1 ........ xn
Error = Exact value - approximate value
Calculation:
Given:
Since the given function is second-degree polynomial.
Simpson's 1/3 rd rule also uses a second degree polynomial for approximation.
Hence there will be no error in the result
The value of Is and Ie will be the same and hence
e = 100 × (Ie - Is)/Ie = 0
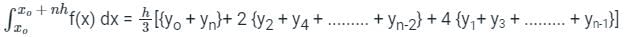
h = width of interval / step length
yo, y1 ........ yn - ordinates corresponding to xo, x1 ........ xn
Error = Exact value - approximate value
Calculation:
Given:
Since the given function is second-degree polynomial.
Simpson's 1/3 rd rule also uses a second degree polynomial for approximation.
Hence there will be no error in the result
The value of Is and Ie will be the same and hence
e = 100 × (Ie - Is)/Ie = 0
The Newton-Raphson method is to be used to determine the reciprocal of the number x = 4. If we start with the initial guess 0.20 then after the first iteration the reciprocal is- a)0.23
- b)0.24
- c)0.25
- d)0.26
Correct answer is option 'B'. Can you explain this answer?
The Newton-Raphson method is to be used to determine the reciprocal of the number x = 4. If we start with the initial guess 0.20 then after the first iteration the reciprocal is
a)
0.23
b)
0.24
c)
0.25
d)
0.26

|
Mihir Kulkarni answered |
Newton-Raphson Method:
The Newton-Raphson method is an iterative numerical method used to find the roots of a given equation. It is based on the principle of linear approximation and uses the tangent line to iteratively approach the root.
Reciprocal of a Number:
The reciprocal of a number x is defined as 1/x. In this case, we are tasked with finding the reciprocal of x = 4.
Initial Guess:
In order to apply the Newton-Raphson method, we need to start with an initial guess. In this case, the initial guess is given as 0.20.
Iteration Process:
The Newton-Raphson method involves iteratively improving the initial guess until an acceptable level of accuracy is achieved. Let's go through the iteration process step by step:
Step 1:
We start with the initial guess: x0 = 0.20
Step 2:
The equation that we want to find the root of is: f(x) = 1/x - 4 = 0
Step 3:
To apply the Newton-Raphson method, we need to find the derivative of f(x) with respect to x. The derivative of 1/x is -1/x^2.
Step 4:
We can now apply the Newton-Raphson formula to update the guess:
x1 = x0 - (f(x0) / f'(x0))
= 0.20 - ((1/0.20 - 4) / (-1/0.20^2))
= 0.20 - ((1/0.20 - 4) / (-1/0.04))
= 0.20 - ((5 - 4) / (-25))
= 0.20 + (1 / 25)
= 0.20 + 0.04
= 0.24
Step 5:
We have now completed the first iteration and obtained a new guess x1 = 0.24.
Conclusion:
After the first iteration of the Newton-Raphson method, the reciprocal of x = 4 is approximately 0.24. Therefore, the correct answer is option 'B'.
The Newton-Raphson method is an iterative numerical method used to find the roots of a given equation. It is based on the principle of linear approximation and uses the tangent line to iteratively approach the root.
Reciprocal of a Number:
The reciprocal of a number x is defined as 1/x. In this case, we are tasked with finding the reciprocal of x = 4.
Initial Guess:
In order to apply the Newton-Raphson method, we need to start with an initial guess. In this case, the initial guess is given as 0.20.
Iteration Process:
The Newton-Raphson method involves iteratively improving the initial guess until an acceptable level of accuracy is achieved. Let's go through the iteration process step by step:
Step 1:
We start with the initial guess: x0 = 0.20
Step 2:
The equation that we want to find the root of is: f(x) = 1/x - 4 = 0
Step 3:
To apply the Newton-Raphson method, we need to find the derivative of f(x) with respect to x. The derivative of 1/x is -1/x^2.
Step 4:
We can now apply the Newton-Raphson formula to update the guess:
x1 = x0 - (f(x0) / f'(x0))
= 0.20 - ((1/0.20 - 4) / (-1/0.20^2))
= 0.20 - ((1/0.20 - 4) / (-1/0.04))
= 0.20 - ((5 - 4) / (-25))
= 0.20 + (1 / 25)
= 0.20 + 0.04
= 0.24
Step 5:
We have now completed the first iteration and obtained a new guess x1 = 0.24.
Conclusion:
After the first iteration of the Newton-Raphson method, the reciprocal of x = 4 is approximately 0.24. Therefore, the correct answer is option 'B'.
The Newton Raphson method is also called as ______- a)Tangent method
- b)Secant method
- c)Chord method
- d)Diameter method
Correct answer is option 'A'. Can you explain this answer?
The Newton Raphson method is also called as ______
a)
Tangent method
b)
Secant method
c)
Chord method
d)
Diameter method
|
|
Anjana Singh answered |
Newton Raphson method is also known as Tangent Method. It is carried out by drawing a tangent to the curve at the point of initial guess.
Find n for the following data if f(0.2) is asked.

- a)0.4
- b)0.2
- c)1
- d)0.1
Correct answer is option 'B'. Can you explain this answer?
Find n for the following data if f(0.2) is asked.


a)
0.4
b)
0.2
c)
1
d)
0.1

|
Pioneer Academy answered |
The formula is
x = x0 + nh.
Here x0 is 0 as 0 is the first element and h is 1.
Since in the question it is given that we have to find f(0.2), x= 0.2.
So, substituting the values in the formula we get,
0.2 = 0 + n(1) .
Hence, n= 0.2.
x = x0 + nh.
Here x0 is 0 as 0 is the first element and h is 1.
Since in the question it is given that we have to find f(0.2), x= 0.2.
So, substituting the values in the formula we get,
0.2 = 0 + n(1) .
Hence, n= 0.2.
While teaching the concept of fractions to students of VI-grade, a teacher performed the following task: Distributed few pieces of paper (circular, rectangular shape) and thread to all the students and ask them to divide them into two parts. The students may divide the paper/thread either into equal or unequal parts. The above scenario indicates which sequential phase of 5 E’s learning model?- a)Evaluation phase
- b)Elaboration phase
- c)Explanation phase
- d)Engagement phase
Correct answer is option 'D'. Can you explain this answer?
While teaching the concept of fractions to students of VI-grade, a teacher performed the following task: Distributed few pieces of paper (circular, rectangular shape) and thread to all the students and ask them to divide them into two parts. The students may divide the paper/thread either into equal or unequal parts. The above scenario indicates which sequential phase of 5 E’s learning model?
a)
Evaluation phase
b)
Elaboration phase
c)
Explanation phase
d)
Engagement phase
|
|
Sanvi Kapoor answered |
The 5 E's learning model, developed by 'Rodger Bybee' is an instructional model based on five stages which are engaging, exploration, explanation, elaboration, and evaluation.
- This constructivist model of learning ensures the active involvement of learners in the teaching-learning process.
Key Points
The 5 E's learning model is briefly explained below:
The 5 E's learning model is briefly explained below:
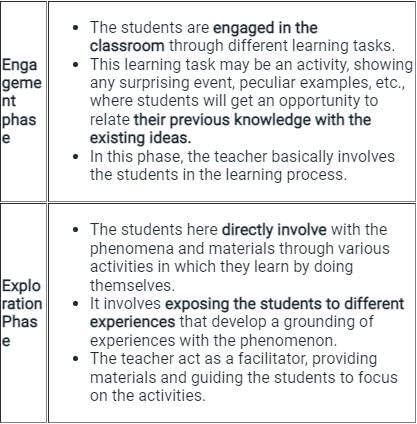
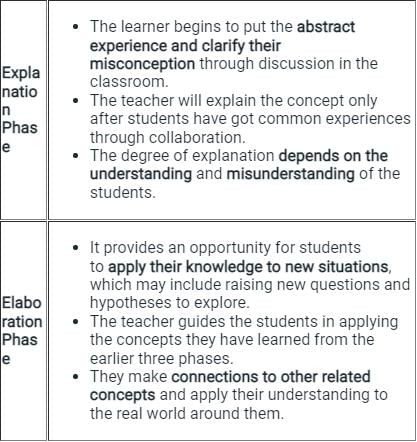

Hence, we can conclude that the above scenario relates to the Engagement Phase of 5 E's model of learning.
If the equation y=axb can be written in the linear form Y=A+BX, what are Y, X, A, B?- a)Y=logy, A=loga, B=b and X=logx
- b)Y=y, A=a, B=b and X=x
- c)Y=y, A=a, B=logb and X=logx
- d)Y=logy, A=a, B=logb and X=x
Correct answer is option 'A'. Can you explain this answer?
If the equation y=axb can be written in the linear form Y=A+BX, what are Y, X, A, B?
a)
Y=logy, A=loga, B=b and X=logx
b)
Y=y, A=a, B=b and X=x
c)
Y=y, A=a, B=logb and X=logx
d)
Y=logy, A=a, B=logb and X=x

|
Jaya Yadav answered |
Explanation:
To understand the given equation and its linear form, let's break down the components:
Given equation: y = ax^b
Linear form: Y = A BX
Components of the linear form:
- Y: Dependent variable (output variable)
- X: Independent variable (input variable)
- A: Intercept (constant)
- B: Slope (coefficient)
Now, let's compare the given equation with the linear form:
Comparison:
- y = ax^b (given equation)
- Y = A BX (linear form)
Dependent Variable:
In the given equation, the dependent variable is "y". Similarly, in the linear form, the dependent variable is "Y".
Independent Variable:
In the given equation, the independent variable is "x". Similarly, in the linear form, the independent variable is "X".
Intercept:
In the given equation, there is no intercept term explicitly mentioned. However, in the linear form, the intercept term is denoted by "A".
Slope:
In the given equation, the coefficient of "x" is denoted as "a". Similarly, in the linear form, the coefficient of "X" is denoted as "B".
Transformation:
To transform the given equation into the linear form, we need to take logarithms of both sides:
log(y) = log(ax^b)
Resultant equation:
By applying the logarithmic transformation, the equation becomes:
Y = log(y)
X = log(x)
A = log(a)
B = b
Therefore, the correct answer is option 'A':
Y = log(y)
X = log(x)
A = log(a)
B = b
To understand the given equation and its linear form, let's break down the components:
Given equation: y = ax^b
Linear form: Y = A BX
Components of the linear form:
- Y: Dependent variable (output variable)
- X: Independent variable (input variable)
- A: Intercept (constant)
- B: Slope (coefficient)
Now, let's compare the given equation with the linear form:
Comparison:
- y = ax^b (given equation)
- Y = A BX (linear form)
Dependent Variable:
In the given equation, the dependent variable is "y". Similarly, in the linear form, the dependent variable is "Y".
Independent Variable:
In the given equation, the independent variable is "x". Similarly, in the linear form, the independent variable is "X".
Intercept:
In the given equation, there is no intercept term explicitly mentioned. However, in the linear form, the intercept term is denoted by "A".
Slope:
In the given equation, the coefficient of "x" is denoted as "a". Similarly, in the linear form, the coefficient of "X" is denoted as "B".
Transformation:
To transform the given equation into the linear form, we need to take logarithms of both sides:
log(y) = log(ax^b)
Resultant equation:
By applying the logarithmic transformation, the equation becomes:
Y = log(y)
X = log(x)
A = log(a)
B = b
Therefore, the correct answer is option 'A':
Y = log(y)
X = log(x)
A = log(a)
B = b
If the equation y = aebx can be written in linear form Y = A + BX, what are Y, X, A, B?- a)Y = logy, A = loga, B=b and X=x
- b)Y = y, A = a, B=b and X=x
- c)Y = y, A = a, B=logb and X=logx
- d)Y = logy, A = a, B=logb and X=x
Correct answer is option 'A'. Can you explain this answer?
If the equation y = aebx can be written in linear form Y = A + BX, what are Y, X, A, B?
a)
Y = logy, A = loga, B=b and X=x
b)
Y = y, A = a, B=b and X=x
c)
Y = y, A = a, B=logb and X=logx
d)
Y = logy, A = a, B=logb and X=x

|
Arya Menon answered |
To understand why option 'A' is the correct answer, let's break down the given equation and the linear form.
Given equation: y = aebx
Linear form: Y = A BX
Now, let's analyze each variable in the given equation and the linear form.
1. Variable 'y':
In the given equation, 'y' represents the dependent variable, which is usually the output or the response variable.
2. Variable 'a':
In the given equation, 'a' represents a constant. It is the initial value of 'y' when 'x' is zero. This constant determines the vertical shift of the graph.
3. Variable 'b':
In the given equation, 'b' represents the rate of change. It determines the steepness or the slope of the graph.
4. Variable 'x':
In the given equation, 'x' represents the independent variable, which is usually the input or the explanatory variable.
Now, let's compare the given equation with the linear form.
Comparing the given equation (y = aebx) with the linear form (Y = A BX), we can see that the variables 'Y' and 'X' in the linear form correspond to 'y' and 'x' in the given equation, respectively.
Therefore, the correct option is 'A' because it correctly identifies the variables in the linear form as:
- Y = logy (corresponding to 'y')
- A = loga (corresponding to 'a')
- B = b (corresponding to 'b')
- X = x (corresponding to 'x')
This interpretation is consistent with the given equation y = aebx, where 'a' and 'b' are constants, and 'x' is the independent variable. The logarithmic form in option 'A' accurately represents the exponential relationship between 'y' and 'x'.
Given equation: y = aebx
Linear form: Y = A BX
Now, let's analyze each variable in the given equation and the linear form.
1. Variable 'y':
In the given equation, 'y' represents the dependent variable, which is usually the output or the response variable.
2. Variable 'a':
In the given equation, 'a' represents a constant. It is the initial value of 'y' when 'x' is zero. This constant determines the vertical shift of the graph.
3. Variable 'b':
In the given equation, 'b' represents the rate of change. It determines the steepness or the slope of the graph.
4. Variable 'x':
In the given equation, 'x' represents the independent variable, which is usually the input or the explanatory variable.
Now, let's compare the given equation with the linear form.
Comparing the given equation (y = aebx) with the linear form (Y = A BX), we can see that the variables 'Y' and 'X' in the linear form correspond to 'y' and 'x' in the given equation, respectively.
Therefore, the correct option is 'A' because it correctly identifies the variables in the linear form as:
- Y = logy (corresponding to 'y')
- A = loga (corresponding to 'a')
- B = b (corresponding to 'b')
- X = x (corresponding to 'x')
This interpretation is consistent with the given equation y = aebx, where 'a' and 'b' are constants, and 'x' is the independent variable. The logarithmic form in option 'A' accurately represents the exponential relationship between 'y' and 'x'.
A thermometer is calibrated 150°C to 200°C. The accuracy is specified within ± 0.25%. What is the maximum static error?- a)± 0.125°C
- b)± 0.216°C
- c)± 0.315°C
- d)± 0.250°C
Correct answer is option 'A'. Can you explain this answer?
A thermometer is calibrated 150°C to 200°C. The accuracy is specified within ± 0.25%. What is the maximum static error?
a)
± 0.125°C
b)
± 0.216°C
c)
± 0.315°C
d)
± 0.250°C

|
Sonal Tiwari answered |
It is unclear what unit of measurement the thermometer is calibrated in. The number "150" without any units does not provide enough information to determine the scale of the thermometer.
The normal equations for a second degree parabola y = ax2 + bx + c are Σy = aΣx2 + bΣx + nc, Σxy = aΣx3 + bΣx2 + cΣx and Σx2y = aΣx4 + bΣx3 + cΣx2.. Is it true or false?- a)True
- b)False
Correct answer is option 'A'. Can you explain this answer?
The normal equations for a second degree parabola y = ax2 + bx + c are Σy = aΣx2 + bΣx + nc, Σxy = aΣx3 + bΣx2 + cΣx and Σx2y = aΣx4 + bΣx3 + cΣx2.. Is it true or false?
a)
True
b)
False

|
Sneha Nair answered |
The normal equations for a second degree parabola y = ax^2 + bx + c are:
1) ∂E/∂a = 0, where E is the error function defined as the sum of squared differences between the actual y-values and the predicted y-values for a given set of x-values. This equation gives the derivative of E with respect to a, and setting it to 0 gives the value of a that minimizes the error.
2) ∂E/∂b = 0, where ∂E/∂b is the derivative of E with respect to b, and setting it to 0 gives the value of b that minimizes the error.
3) ∂E/∂c = 0, where ∂E/∂c is the derivative of E with respect to c, and setting it to 0 gives the value of c that minimizes the error.
These equations can be solved simultaneously to find the values of a, b, and c that best fit the given data points.
1) ∂E/∂a = 0, where E is the error function defined as the sum of squared differences between the actual y-values and the predicted y-values for a given set of x-values. This equation gives the derivative of E with respect to a, and setting it to 0 gives the value of a that minimizes the error.
2) ∂E/∂b = 0, where ∂E/∂b is the derivative of E with respect to b, and setting it to 0 gives the value of b that minimizes the error.
3) ∂E/∂c = 0, where ∂E/∂c is the derivative of E with respect to c, and setting it to 0 gives the value of c that minimizes the error.
These equations can be solved simultaneously to find the values of a, b, and c that best fit the given data points.
Find the difference between the sum of (x + y + z) and the Trace upper triangular matrix formed by using the gauss elimination method.
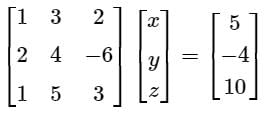
- a)6
- b)8
- c)10
- d)12
Correct answer is option 'C'. Can you explain this answer?
Find the difference between the sum of (x + y + z) and the Trace upper triangular matrix formed by using the gauss elimination method.
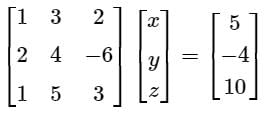
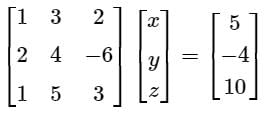
a)
6
b)
8
c)
10
d)
12

|
Vertex Academy answered |
Concept:
Gauss elimination method,
In this method, an augmented matrix is formed by the coefficient of x, y, & z then,
By using row transformation, it is converted into an upper triangular matrix.
Calculation:
AX = B

R2 → R2 - 2R1
R3 → R3 - R1

R3 → R3 + R2
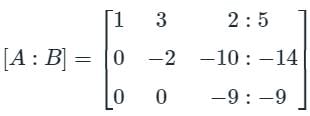
Now, again converting this matrix into equation,
x + 3y + 2z = 5
-2y - 10z = -14
-9z = -9
on solving
z= 1, y = 2 & x = -3
x + y + z = -3 + 2 + 1 = 0
Trace of upper traingular matrix = 1 - 2 - 9 = -10
Difference = ( x + y + z ) - trace = 0- (-10 =)
Difference = 10
Gauss elimination method,
In this method, an augmented matrix is formed by the coefficient of x, y, & z then,
By using row transformation, it is converted into an upper triangular matrix.
Calculation:
AX = B

R2 → R2 - 2R1
R3 → R3 - R1

R3 → R3 + R2
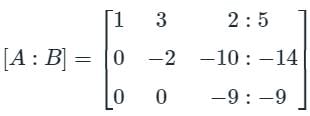
Now, again converting this matrix into equation,
x + 3y + 2z = 5
-2y - 10z = -14
-9z = -9
on solving
z= 1, y = 2 & x = -3
x + y + z = -3 + 2 + 1 = 0
Trace of upper traingular matrix = 1 - 2 - 9 = -10
Difference = ( x + y + z ) - trace = 0- (-10 =)
Difference = 10
Newton- Gregory Forward interpolation formula can be used _______- a)only for equally spaced intervals
- b)only for unequally spaced intervals
- c)for both equally and unequally spaced intervals
- d)for unequally intervals
Correct answer is option 'A'. Can you explain this answer?
Newton- Gregory Forward interpolation formula can be used _______
a)
only for equally spaced intervals
b)
only for unequally spaced intervals
c)
for both equally and unequally spaced intervals
d)
for unequally intervals
|
|
Anjana Singh answered |
Newton – Gregory Forward Interpolation formula is given by
f(x) = y0 + nΔy0 + n(n-1)Δ2y0/2! + n(n-1)(n-2) Δ3y0 /3! + …..
This formula is obtained by the Newton’s Divided difference formula by substituting the intervals as h. This is done because we assume the intervals to be constant, that is, equally spaced.
f(x) = y0 + nΔy0 + n(n-1)Δ2y0/2! + n(n-1)(n-2) Δ3y0 /3! + …..
This formula is obtained by the Newton’s Divided difference formula by substituting the intervals as h. This is done because we assume the intervals to be constant, that is, equally spaced.
Find x if x0 = 0.6, n = 2.6 and h = 0.2.- a)12
- b)1.2
- c)1.12
- d)1.22
Correct answer is option 'C'. Can you explain this answer?
Find x if x0 = 0.6, n = 2.6 and h = 0.2.
a)
12
b)
1.2
c)
1.12
d)
1.22

|
Anshu Kumar answered |
Given values:
- x0 = 0.6
- n = 2.6
- h = 0.2
Finding x:
To find the value of x, we can use the formula:
x = x0 + n*h
Calculating x:
Given x0 = 0.6, n = 2.6, and h = 0.2
x = 0.6 + 2.6*0.2
x = 0.6 + 0.52
x = 1.12
Therefore, the value of x is 1.12, which corresponds to option C.
- x0 = 0.6
- n = 2.6
- h = 0.2
Finding x:
To find the value of x, we can use the formula:
x = x0 + n*h
Calculating x:
Given x0 = 0.6, n = 2.6, and h = 0.2
x = 0.6 + 2.6*0.2
x = 0.6 + 0.52
x = 1.12
Therefore, the value of x is 1.12, which corresponds to option C.
A function y = 5x2 + 10x is defined over an open interval x = (1, 2). At least at one point in this interval, dy/dx is exactly- a)20
- b)25
- c)30
- d)35
Correct answer is option 'B'. Can you explain this answer?
A function y = 5x2 + 10x is defined over an open interval x = (1, 2). At least at one point in this interval, dy/dx is exactly
a)
20
b)
25
c)
30
d)
35

|
Anshu Kumar answered |
Understanding the Function
The function given is y = 5x² + 10x. We need to find the derivative dy/dx to analyze its behavior over the interval (1, 2).
Calculating the Derivative
To find dy/dx:
- Differentiate the function:
- dy/dx = d/dx (5x² + 10x)
- dy/dx = 10x + 10
Evaluating the Derivative
Now, we will evaluate the derivative at the endpoints of the interval (1, 2):
- For x = 1:
- dy/dx = 10(1) + 10 = 20
- For x = 2:
- dy/dx = 10(2) + 10 = 30
Applying the Mean Value Theorem
According to the Mean Value Theorem, since the function is continuous and differentiable over the open interval (1, 2), there exists at least one point c in (1, 2) such that:
- dy/dx = (y(2) - y(1)) / (2 - 1)
Calculating y(1) and y(2)
- y(1) = 5(1)² + 10(1) = 15
- y(2) = 5(2)² + 10(2) = 40
Finding the Average Rate of Change
Now, calculate the average rate of change:
- Average Rate = (40 - 15) / (2 - 1) = 25
Conclusion
Since dy/dx varies linearly between the endpoints and includes the average rate of change (25), it confirms that at least one point in the interval has a derivative of exactly 25. Thus, the correct answer is option 'B'.
The function given is y = 5x² + 10x. We need to find the derivative dy/dx to analyze its behavior over the interval (1, 2).
Calculating the Derivative
To find dy/dx:
- Differentiate the function:
- dy/dx = d/dx (5x² + 10x)
- dy/dx = 10x + 10
Evaluating the Derivative
Now, we will evaluate the derivative at the endpoints of the interval (1, 2):
- For x = 1:
- dy/dx = 10(1) + 10 = 20
- For x = 2:
- dy/dx = 10(2) + 10 = 30
Applying the Mean Value Theorem
According to the Mean Value Theorem, since the function is continuous and differentiable over the open interval (1, 2), there exists at least one point c in (1, 2) such that:
- dy/dx = (y(2) - y(1)) / (2 - 1)
Calculating y(1) and y(2)
- y(1) = 5(1)² + 10(1) = 15
- y(2) = 5(2)² + 10(2) = 40
Finding the Average Rate of Change
Now, calculate the average rate of change:
- Average Rate = (40 - 15) / (2 - 1) = 25
Conclusion
Since dy/dx varies linearly between the endpoints and includes the average rate of change (25), it confirms that at least one point in the interval has a derivative of exactly 25. Thus, the correct answer is option 'B'.
Chapter doubts & questions for Numerical Methods - Engineering Mathematics 2025 is part of Engineering Mathematics exam preparation. The chapters have been prepared according to the Engineering Mathematics exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Engineering Mathematics 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Numerical Methods - Engineering Mathematics in English & Hindi are available as part of Engineering Mathematics exam.
Download more important topics, notes, lectures and mock test series for Engineering Mathematics Exam by signing up for free.
Engineering Mathematics
65 videos|133 docs|94 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup









