All Exams >
Computer Science Engineering (CSE) >
Algorithms >
All Questions
All questions of Graph Based Algorithms for Computer Science Engineering (CSE) Exam
Consider the following directed graph: 
The number of different topological orderings of the vertices of the graph is _____________.
Correct answer is '6'. Can you explain this answer?
Consider the following directed graph:
The number of different topological orderings of the vertices of the graph is _____________.
|
Yash Patel answered |
Here Start with a and End with f.
a _ _ _ _ f
Blanks spaces are to be filled with b, c, d, e such that b comes before c, and d comes before e..
Number of ways to arrange b,c,d,e such that b comes before c and d comes before e. will be = 4!/(2!*2!) = 6
Number of ways to arrange b,c,d,e such that b comes before c and d comes before e. will be = 4!/(2!*2!) = 6
In a depth-first traversal of a graph G with n vertices, k edges are marked as tree edges. The number of connected components in G is- a)k
- b) k + 1
- c)n - k - 1
- d)n - k
Correct answer is option 'D'. Can you explain this answer?
In a depth-first traversal of a graph G with n vertices, k edges are marked as tree edges. The number of connected components in G is
a)
k
b)
k + 1
c)
n - k - 1
d)
n - k
|
|
Yash Patel answered |
Tree edges are the edges that are part of DFS tree. If there are x tree edges in a tree, then x+1 vertices in the tree. The output of DFS is a forest if the graph is disconnected. Let us see below simple example where graph is disconnected.
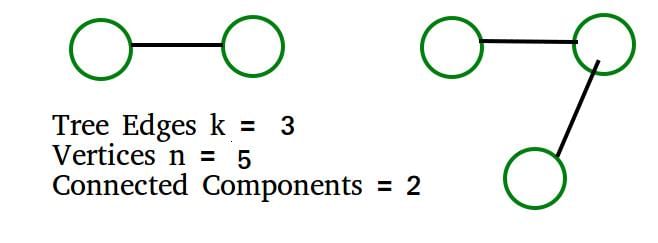
The above example matches with D option More Examples:
1) All vertices of Graph are connected. k must be n-1. We get number of connected components = n- k = n - (n-1) = 1
2) No vertex is connected. k must be 0. We get number of connected components = n- k = n - 0 = n
What are the appropriate data structures for following algorithms?
1) Breadth First Search
2) Depth First Search
3) Prim's Minimum Spanning Tree
4) Kruskal' Minimum Spanning Tree - a)1) Stack
2) Queue
3) Priority Queue
4) Union Find - b)1) Queue
2) Stack
3) Priority Queue
4) Union Find - c)1) Stack
2) Queue
3) Union Find
4) Priority Queue - d)1) Priority Queue
2) Queue
3) Stack
4) Union Find
Correct answer is option 'B'. Can you explain this answer?
What are the appropriate data structures for following algorithms?
1) Breadth First Search
2) Depth First Search
3) Prim's Minimum Spanning Tree
4) Kruskal' Minimum Spanning Tree
1) Breadth First Search
2) Depth First Search
3) Prim's Minimum Spanning Tree
4) Kruskal' Minimum Spanning Tree
a)
1) Stack
2) Queue
3) Priority Queue
4) Union Find
2) Queue
3) Priority Queue
4) Union Find
b)
1) Queue
2) Stack
3) Priority Queue
4) Union Find
2) Stack
3) Priority Queue
4) Union Find
c)
1) Stack
2) Queue
3) Union Find
4) Priority Queue
2) Queue
3) Union Find
4) Priority Queue
d)
1) Priority Queue
2) Queue
3) Stack
4) Union Find
2) Queue
3) Stack
4) Union Find
|
Sanya Agarwal answered |
1) Breadth First Search uses Queue
2) Depth First Search uses Stack
3) Prim's Minimum Spanning Tree uses Priority Queue.
4) Kruskal' Minimum Spanning Tree uses Union Find.
Let G = (V, G) be a weighted undirected graph and let T be a Minimum Spanning Tree (MST) of G maintained using adjacency lists. Suppose a new weighed edge (u, v) ∈ V×V is added to G. The worst case time complexity of determining if T is still an MST of the resultant graph is- a)θ(∣E∣ + ∣V∣)
- b)θ(∣E∣.∣V∣)
- c)θ(E∣ log ∣V∣)
- d)θ(∣V∣)
Correct answer is option 'D'. Can you explain this answer?
Let G = (V, G) be a weighted undirected graph and let T be a Minimum Spanning Tree (MST) of G maintained using adjacency lists. Suppose a new weighed edge (u, v) ∈ V×V is added to G. The worst case time complexity of determining if T is still an MST of the resultant graph is
a)
θ(∣E∣ + ∣V∣)
b)
θ(∣E∣.∣V∣)
c)
θ(E∣ log ∣V∣)
d)
θ(∣V∣)
|
|
Sanya Agarwal answered |
- As T is a minimum spanning tree and we need to add a new edge to existing spanning tree.
- Later we need to check still T is a minimum spanning tree or not, So we need to check all vertices whether there is any cycle present after adding a new edge.
- All vertices need to traverse to confirm minimum spanning tree after adding new edge then time complexity is O(V).
Option (D) is correct.
Let T be a depth first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true?- a)There must exist a vertex w adjacent to both u and n in G
- b)There must exist a vertex w whose removal disconnects u and n in G
- c)There must exist a cycle in G containing u and n
- d)There must exist a cycle in G containing u and all its neighbours in G.
Correct answer is option 'D'. Can you explain this answer?
Let T be a depth first search tree in an undirected graph G. Vertices u and n are leaves of this tree T. The degrees of both u and n in G are at least 2. which one of the following statements is true?
a)
There must exist a vertex w adjacent to both u and n in G
b)
There must exist a vertex w whose removal disconnects u and n in G
c)
There must exist a cycle in G containing u and n
d)
There must exist a cycle in G containing u and all its neighbours in G.
|
Riverdale Learning Institute answered |
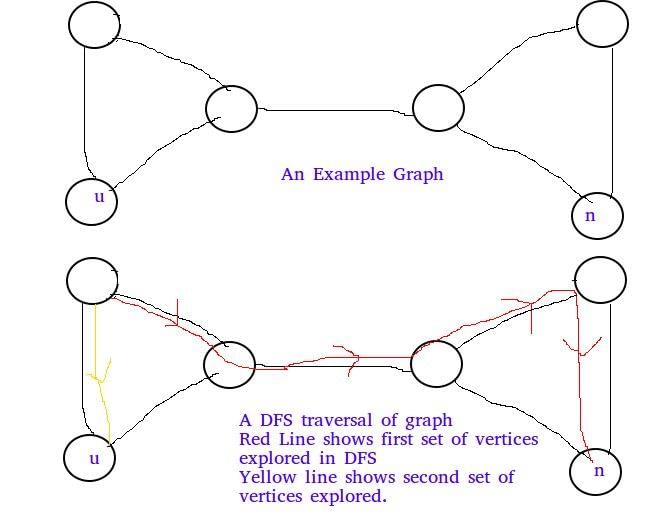
Below example shows that A and B are FALSE:
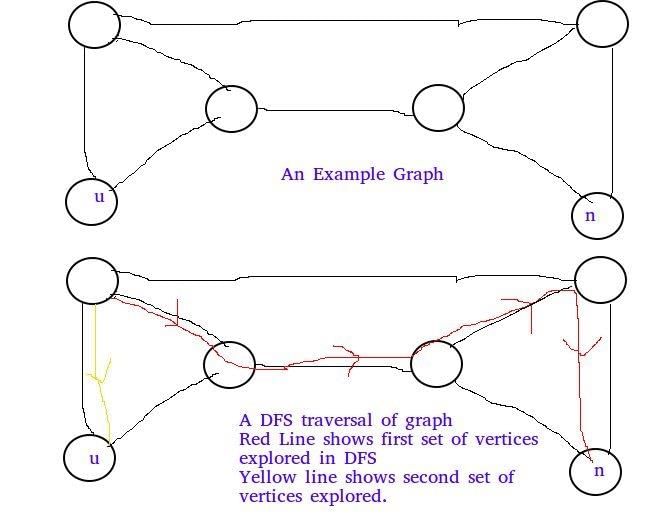
Below example shows C is false:
Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE? - a)There exists a cutset in G having all edges of maximum weight.
- b)There exists a cycle in G having all edges of maximum weight
- c)Edge e cannot be contained in a cycle.
- d)All edges in G have the same weight
Correct answer is option 'A'. Can you explain this answer?
Let G be a weighted undirected graph and e be an edge with maximum weight in G. Suppose there is a minimum weight spanning tree in G containing the edge e. Which of the following statements is always TRUE?
a)
There exists a cutset in G having all edges of maximum weight.
b)
There exists a cycle in G having all edges of maximum weight
c)
Edge e cannot be contained in a cycle.
d)
All edges in G have the same weight
|
Cstoppers Instructors answered |
Background : Given a connected and undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together.
- A spanning tree has exactly V - 1 edges.
- A single graph can have many different spanning trees. A minimum spanning tree (MST) or minimum weight spanning tree for a weighted, connected and undirected graph is a spanning tree with weight less than or equal to the weight of every other spanning tree. The weight of a spanning tree is the sum of weights given to each edge of the spanning tree.
- There can be more that one possible spanning trees of a graph. For example, the graph in this question has 6 possible spanning trees.
- MST has lightest edge of every cutset. Remember Prim's algorithm which basically picks the lightest edge from every cutset.
Choices of this question :
a) There exists a cutset in G having all edges of maximum weight : This is correct. If there is a heaviest edge in MST, then there exist a cut with all edges with weight equal to heavies edge. See point 4 discussed in above background.
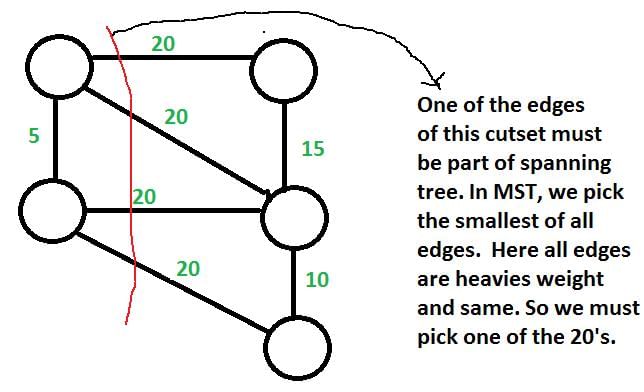
b) There exists a cycle in G having all edges of maximum weight : Not always TRUE. The cutset of heaviest edge may contain only one edge. In fact there may be overall one edge of heavies weight which is part of MST (Consider a graph with two components which are connected by only one edge and this edge is the heavies)
c) Edge e cannot be contained in a cycle. Not Always True. The curset may form cycle with other edges. d) All edges in G have the same weight Not always True. As discussed in option b, there can be only one edge of heaviest weight.
Which of the following statements is false?- a)Optimal binary search tree construction can be performed efficiently using dynamic programming
- b)Breadth-first search cannot be used to find connected components of a graph
- c)Given the prefix and postfix walks over a binary tree, the binary tree cannot be uniquely constructed.
- d)Depth-first search can be used to find connected components of a graph
Correct answer is option 'B'. Can you explain this answer?
Which of the following statements is false?
a)
Optimal binary search tree construction can be performed efficiently using dynamic programming
b)
Breadth-first search cannot be used to find connected components of a graph
c)
Given the prefix and postfix walks over a binary tree, the binary tree cannot be uniquely constructed.
d)
Depth-first search can be used to find connected components of a graph
|
Palak Saini answered |
(a) True.
(b) False.
(c) True.
(d) True.
(b) False.
(c) True.
(d) True.
Let G be an undirected graph. Consider a depth-first traversal of G, and let T be the resulting depth-first search tree. Let u be a vertex in G and let v be the first new (unvisited) vertex visited after visiting u in the traversal. Which of the following statements is always true?- a){u,v} must be an edge in G, and u is a descendant of v in T
- b){u,v} must be an edge in G, and v is a descendant of u in T
- c)If {u,v} is not an edge in G then u is a leaf in T
- d)If {u,v} is not an edge in G then u and v must have the same parent in T
Correct answer is option 'C'. Can you explain this answer?
Let G be an undirected graph. Consider a depth-first traversal of G, and let T be the resulting depth-first search tree. Let u be a vertex in G and let v be the first new (unvisited) vertex visited after visiting u in the traversal. Which of the following statements is always true?
a)
{u,v} must be an edge in G, and u is a descendant of v in T
b)
{u,v} must be an edge in G, and v is a descendant of u in T
c)
If {u,v} is not an edge in G then u is a leaf in T
d)
If {u,v} is not an edge in G then u and v must have the same parent in T
|
Samridhi Ahuja answered |
Explanation:
Depth-first traversal:
- In a depth-first traversal of a graph, we start at a chosen vertex and explore as far as possible along each branch before backtracking.
- This results in a depth-first search tree T, where each edge in T corresponds to a discovery edge in the original graph G.
Statement C explanation:
- If {u,v} is not an edge in G, it means that vertex v was not adjacent to vertex u in G.
- In the depth-first traversal, if v is the first new vertex visited after u, it implies that v is a leaf in the depth-first search tree T.
- This is because if v had any other children in T, we would have visited them before v, as we explore as far as possible along each branch before backtracking.
- Therefore, if {u,v} is not an edge in G, u must be a leaf in T.
Therefore, statement C is always true.
Depth-first traversal:
- In a depth-first traversal of a graph, we start at a chosen vertex and explore as far as possible along each branch before backtracking.
- This results in a depth-first search tree T, where each edge in T corresponds to a discovery edge in the original graph G.
Statement C explanation:
- If {u,v} is not an edge in G, it means that vertex v was not adjacent to vertex u in G.
- In the depth-first traversal, if v is the first new vertex visited after u, it implies that v is a leaf in the depth-first search tree T.
- This is because if v had any other children in T, we would have visited them before v, as we explore as far as possible along each branch before backtracking.
- Therefore, if {u,v} is not an edge in G, u must be a leaf in T.
Therefore, statement C is always true.
Consider a directed graph with n vertices and m edges such that all edges have same edge weights. Find the complexity of the best known algorithm to compute the minimum spanning tree of the graph?- a)O(m+n)
- b)O(m logn)
- c)O(mn)
- d)O(n logm)
Correct answer is option 'A'. Can you explain this answer?
Consider a directed graph with n vertices and m edges such that all edges have same edge weights. Find the complexity of the best known algorithm to compute the minimum spanning tree of the graph?
a)
O(m+n)
b)
O(m logn)
c)
O(mn)
d)
O(n logm)
|
Ravi Singh answered |
It’s a special case in which all edge weights are equal, so dfs would work and resultant depth first tree would be the spanning tree. So the answer would be O(m+n).
Given two vertices in a graph s and t, which of the two traversals (BFS and DFS) can be used to find if there is path from s to t?- a)Only BFS
- b)Only DFS
- c)Both BFS and DFS
- d)Neither BFS nor DFS
Correct answer is option 'C'. Can you explain this answer?
Given two vertices in a graph s and t, which of the two traversals (BFS and DFS) can be used to find if there is path from s to t?
a)
Only BFS
b)
Only DFS
c)
Both BFS and DFS
d)
Neither BFS nor DFS
|
Aditi Pillai answered |
Explanation:
Both BFS and DFS can be used to find if there is a path from s to t in a graph:
- BFS (Breadth-First Search): BFS explores all the neighboring nodes of a vertex before moving on to the next level. By performing BFS from vertex s, we can check if vertex t is reachable from s. If t is discovered during the BFS traversal, then there exists a path from s to t.
- DFS (Depth-First Search): DFS explores as far as possible along each branch before backtracking. By performing DFS from vertex s, we can check if vertex t is reachable from s. If during the DFS traversal, we encounter vertex t, then there exists a path from s to t.
Both BFS and DFS are traversal algorithms that can be used to explore paths in a graph. Depending on the specific characteristics of the graph and the requirements of the problem, either BFS or DFS may be preferred for finding a path from s to t.
Both BFS and DFS can be used to find if there is a path from s to t in a graph:
- BFS (Breadth-First Search): BFS explores all the neighboring nodes of a vertex before moving on to the next level. By performing BFS from vertex s, we can check if vertex t is reachable from s. If t is discovered during the BFS traversal, then there exists a path from s to t.
- DFS (Depth-First Search): DFS explores as far as possible along each branch before backtracking. By performing DFS from vertex s, we can check if vertex t is reachable from s. If during the DFS traversal, we encounter vertex t, then there exists a path from s to t.
Both BFS and DFS are traversal algorithms that can be used to explore paths in a graph. Depending on the specific characteristics of the graph and the requirements of the problem, either BFS or DFS may be preferred for finding a path from s to t.
Which one of the following algorithm design techniques is used in finding all pairs of shortest distances in a graph?- a)Dynamic programming
- b)Backtracking
- c)Greedy
- d)Divide and Conquer
Correct answer is option 'A'. Can you explain this answer?
Which one of the following algorithm design techniques is used in finding all pairs of shortest distances in a graph?
a)
Dynamic programming
b)
Backtracking
c)
Greedy
d)
Divide and Conquer
|
Palak Khanna answered |
Answer is A because floyd warshall algorithm used to find all shortest path which is a dynamic programming approach.
Consider the tree arcs of a BFS traversal from a source node W in an unweighted, connected, undirected graph. The tree T formed by the tree arcs is a data structure for computing- a)the shortest path between every pair of vertices.
- b)the shortest path W from to every vertex in the graph.
- c)the shortest paths from W to only those nodes that are leaves of T
- d)the longest path in the graph.
Correct answer is option 'B'. Can you explain this answer?
Consider the tree arcs of a BFS traversal from a source node W in an unweighted, connected, undirected graph. The tree T formed by the tree arcs is a data structure for computing
a)
the shortest path between every pair of vertices.
b)
the shortest path W from to every vertex in the graph.
c)
the shortest paths from W to only those nodes that are leaves of T
d)
the longest path in the graph.
|
|
Diya Chauhan answered |
BFS always having starting node. It does not calculate shortest path between every pair but it computes shorted path between W and any other vertex ..
Let G be a simple graph with 20 vertices and 8 components. If we delete a vertex in G, then number of components in G should lie between ____.- a)8 and 20
- b)8 and 19
- c)7 and 19
- d)7 and 20
Correct answer is option 'C'. Can you explain this answer?
Let G be a simple graph with 20 vertices and 8 components. If we delete a vertex in G, then number of components in G should lie between ____.
a)
8 and 20
b)
8 and 19
c)
7 and 19
d)
7 and 20
|
|
Ravi Singh answered |
Case 1: If the vertex we are deleting from G is an isolated vertex, which is a component by itself, then number of components in G becomes 7.
Case 2: If G is a start Graph, then by deleting the cut vertex of G, we get 19 components.
Hence, number of components in G should lie between 7 and 19.
Case 2: If G is a start Graph, then by deleting the cut vertex of G, we get 19 components.
Hence, number of components in G should lie between 7 and 19.
Let G be an undirected graph. Consider a depth-first traversal of G, and let T be the resulting depth-first search tree. Let u be a vertex in G and let v be the first new (unvisited) vertex visited after visiting u in the traversal. Which of the following statement is always true?
- a){u, v} must be an edge in G, and u is a descendant of v in T
- b){u, v} must be an edge in G, and v is a descendant of u in T
- c)If {u, v} is not an edge in G then u and v must have the same parent in T
- d)If {u, v} is not an edge in G then u is a leaf in T
Correct answer is option 'D'. Can you explain this answer?
Let G be an undirected graph. Consider a depth-first traversal of G, and let T be the resulting depth-first search tree. Let u be a vertex in G and let v be the first new (unvisited) vertex visited after visiting u in the traversal. Which of the following statement is always true?
a)
{u, v} must be an edge in G, and u is a descendant of v in T
b)
{u, v} must be an edge in G, and v is a descendant of u in T
c)
If {u, v} is not an edge in G then u and v must have the same parent in T
d)
If {u, v} is not an edge in G then u is a leaf in T
|
Arindam Malik answered |
Explanation:
In a depth-first traversal of an undirected graph G, we start at a given vertex and explore as far as possible along each branch before backtracking.
Depth-First Search (DFS):
- Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures.
- The algorithm starts at a specified vertex and explores as far as possible along each branch before backtracking.
- It uses a stack to remember which vertices to visit next.
Depth-First Search Tree (T):
- The depth-first search tree T is a directed graph formed during the depth-first traversal of the original undirected graph G.
- In T, each vertex is visited only once.
- T contains all the vertices of G and a subset of the edges of G.
First New Vertex (v) Visited After u:
- Let u be a vertex in G and v be the first new (unvisited) vertex visited after visiting u in the traversal.
- This means that v is the next vertex encountered in the depth-first search after visiting u.
Statement Options:
a) {u, v} must be an edge in G, and u is a descendant of v in T.
b) {u, v} must be an edge in G, and v is a descendant of u in T.
c) If {u, v} is not an edge in G then u and v must have the same parent in T.
d) If {u, v} is not an edge in G then u is a leaf in T.
Analysis of Statement Options:
a) {u, v} must be an edge in G, and u is a descendant of v in T.
- This statement is not always true because {u, v} does not necessarily have to be an edge in G.
- It is possible for v to be a vertex that is not connected to u by an edge in G.
b) {u, v} must be an edge in G, and v is a descendant of u in T.
- This statement is not always true because {u, v} does not necessarily have to be an edge in G.
- It is possible for v to be a vertex that is not connected to u by an edge in G.
c) If {u, v} is not an edge in G then u and v must have the same parent in T.
- This statement is not always true because u and v can have different parents in T.
- It is possible for u and v to be connected in T through another path that does not involve their immediate parent-child relationship.
d) If {u, v} is not an edge in G then u is a leaf in T.
- This statement is always true because if {u, v} is not an edge in G, it means that u and v are not connected in G.
- In the depth-first traversal, after visiting u, if v is the first new vertex encountered, it means that there are no more unvisited vertices connected to u.
- Therefore, u does not have any outgoing edges in T and is a leaf in T.
Conclusion:
The correct answer is option 'D'. If {u, v} is not an edge in G, then u is a leaf in T.
In a depth-first traversal of an undirected graph G, we start at a given vertex and explore as far as possible along each branch before backtracking.
Depth-First Search (DFS):
- Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures.
- The algorithm starts at a specified vertex and explores as far as possible along each branch before backtracking.
- It uses a stack to remember which vertices to visit next.
Depth-First Search Tree (T):
- The depth-first search tree T is a directed graph formed during the depth-first traversal of the original undirected graph G.
- In T, each vertex is visited only once.
- T contains all the vertices of G and a subset of the edges of G.
First New Vertex (v) Visited After u:
- Let u be a vertex in G and v be the first new (unvisited) vertex visited after visiting u in the traversal.
- This means that v is the next vertex encountered in the depth-first search after visiting u.
Statement Options:
a) {u, v} must be an edge in G, and u is a descendant of v in T.
b) {u, v} must be an edge in G, and v is a descendant of u in T.
c) If {u, v} is not an edge in G then u and v must have the same parent in T.
d) If {u, v} is not an edge in G then u is a leaf in T.
Analysis of Statement Options:
a) {u, v} must be an edge in G, and u is a descendant of v in T.
- This statement is not always true because {u, v} does not necessarily have to be an edge in G.
- It is possible for v to be a vertex that is not connected to u by an edge in G.
b) {u, v} must be an edge in G, and v is a descendant of u in T.
- This statement is not always true because {u, v} does not necessarily have to be an edge in G.
- It is possible for v to be a vertex that is not connected to u by an edge in G.
c) If {u, v} is not an edge in G then u and v must have the same parent in T.
- This statement is not always true because u and v can have different parents in T.
- It is possible for u and v to be connected in T through another path that does not involve their immediate parent-child relationship.
d) If {u, v} is not an edge in G then u is a leaf in T.
- This statement is always true because if {u, v} is not an edge in G, it means that u and v are not connected in G.
- In the depth-first traversal, after visiting u, if v is the first new vertex encountered, it means that there are no more unvisited vertices connected to u.
- Therefore, u does not have any outgoing edges in T and is a leaf in T.
Conclusion:
The correct answer is option 'D'. If {u, v} is not an edge in G, then u is a leaf in T.
Let G be an undirected graph. Consider a depth-first traversal of G, and let T be the resulting depth-first search tree. Let u be a vertex in G and let v be the first new (unvisited) vertex visited after visiting u in the traversal. Which of the following statements is always true?- a){u,v} must be an edge in G, and u is a descendant of v in T
- b){u,v} must be an edge in G, and v is a descendant of u in T
- c)If {u,v} is not an edge in G then u is a leaf in T
- d)If {u,v} is not an edge in G then u and v must have the same parent in T
Correct answer is option 'C'. Can you explain this answer?
Let G be an undirected graph. Consider a depth-first traversal of G, and let T be the resulting depth-first search tree. Let u be a vertex in G and let v be the first new (unvisited) vertex visited after visiting u in the traversal. Which of the following statements is always true?
a)
{u,v} must be an edge in G, and u is a descendant of v in T
b)
{u,v} must be an edge in G, and v is a descendant of u in T
c)
If {u,v} is not an edge in G then u is a leaf in T
d)
If {u,v} is not an edge in G then u and v must have the same parent in T
|
|
Sanya Agarwal answered |
In DFS, if 'v' is visited
after 'u', then one of the following is true.
1) (u, v) is an edge.
u
/ \
v w
/ / \
x y z
after 'u', then one of the following is true.
1) (u, v) is an edge.
u
/ \
v w
/ / \
x y z
2) 'u' is a leaf node.
w
/ \
x v
/ / \
u y z
In DFS, after visiting a node, we first recur for all unvisited children. If there are no unvisited children (u is leaf), then control goes back to parent and parent then visits next unvisited children.
w
/ \
x v
/ / \
u y z
In DFS, after visiting a node, we first recur for all unvisited children. If there are no unvisited children (u is leaf), then control goes back to parent and parent then visits next unvisited children.
What is the largest integer m such that every simple connected graph with n vertices and n edges contains at least m different spanning trees?- a)1
- b)2
- c)3
- d)n
Correct answer is option 'C'. Can you explain this answer?
What is the largest integer m such that every simple connected graph with n vertices and n edges contains at least m different spanning trees?
a)
1
b)
2
c)
3
d)
n
|
|
Sanya Agarwal answered |
A graph is connected iff all nodes can be traversed from each node. For a graph with n nodes, there will be n-1 minimum number of edges.
Given that there are n edges, that means a cycle is there in the graph.
The simplex graph with these conditions may be:
Given that there are n edges, that means a cycle is there in the graph.
The simplex graph with these conditions may be:
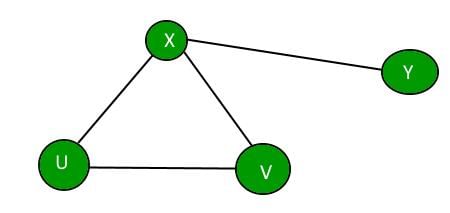
Now we can make a different spanning tree by removing one edge from the cycle, one at a time.
Minimum cycle length can be 3, So, there must be atleast 3 spanning trees in any such Graph.
Minimum cycle length can be 3, So, there must be atleast 3 spanning trees in any such Graph.
In an unweighted, undirected connected graph, the shortest path from a node S to every other node is computed most efficiently, in terms of time complexity, by- a)Dijkstra’s algorithm starting from S.
- b)Warshall’s algorithm.
- c)Performing a DFS starting from S.
- d)Performing a BFS starting from S.
Correct answer is option 'D'. Can you explain this answer?
In an unweighted, undirected connected graph, the shortest path from a node S to every other node is computed most efficiently, in terms of time complexity, by
a)
Dijkstra’s algorithm starting from S.
b)
Warshall’s algorithm.
c)
Performing a DFS starting from S.
d)
Performing a BFS starting from S.
|
Dishani Basu answered |
Dijkastra and warshall 's algo only used for weighted graph.
Both DFS and BFS can be used for finding path between 2 vertices in undirected and unweighted graph but BFS can only give the shortest path as concern in given question so BFS is Ans.
Note :- finding only path(DFS) and finding shortest path(BFS) ..Matters a lot
Given an undirected graph G with V vertices and E edges, the sum of the degrees of all vertices is- a)E
- b)2E
- c)V
- d)2V
Correct answer is option 'B'. Can you explain this answer?
Given an undirected graph G with V vertices and E edges, the sum of the degrees of all vertices is
a)
E
b)
2E
c)
V
d)
2V
|
|
Sanya Agarwal answered |
Since the given graph is undirected, every edge contributes as 2 to sum of degrees. So the sum of degrees is 2E.
The minimum number of record movements required to merge five files A (with 10 records), B (with 20 records), C (with 15 records), D (with 5 records) and E (with 25 records) is:- a)165
- b)90
- c)75
- d)65
Correct answer is option 'A'. Can you explain this answer?
The minimum number of record movements required to merge five files A (with 10 records), B (with 20 records), C (with 15 records), D (with 5 records) and E (with 25 records) is:
a)
165
b)
90
c)
75
d)
65
|
|
Diya Chauhan answered |
Arrange files in increasing order of records
5(D) 10(A)
No of movements=15+30+45+75=165
No of movements=15+30+45+75=165
Let G be the graph with 100 vertices numbered 1 to 100. Two vertices i and j are adjacent iff |i−j|=8 or |i−j|=12. The number of connected components in G is- a)8
- b)4
- c)12
- d)25
Correct answer is option 'B'. Can you explain this answer?
Let G be the graph with 100 vertices numbered 1 to 100. Two vertices i and j are adjacent iff |i−j|=8 or |i−j|=12. The number of connected components in G is
a)
8
b)
4
c)
12
d)
25
|
|
Yash Patel answered |
When vertices are arranged with difference of 8 there are 8 components as shown by 8 columns in the image below:
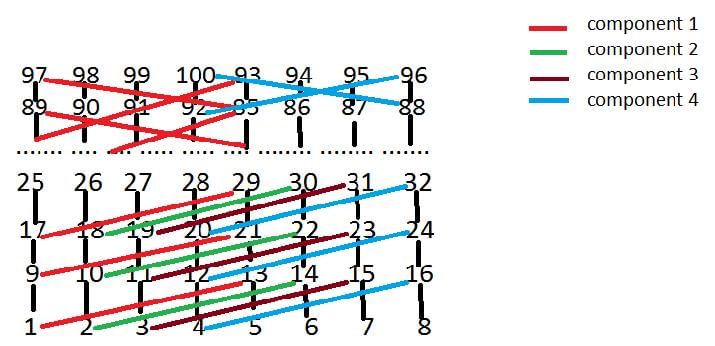
When vertices are arranged withdifference of 12 the number of components is reduced to 4 as first column will be connected with fifth column, second column will be connected with sixth column, third column will be connected with seventh column and fourth column will be connected with eighth column. No other form of connection exists so total 4 connected components are there. So, option (B) is correct. This explanation is contributed by Pradeep Pandey.
Consider the following directed graph.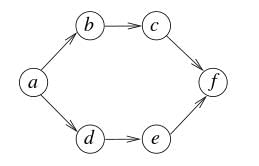
The number of different topological orderings of the vertices of the graph is Note : This question was asked as Numerical Answer Type.- a)1
- b)2
- c)4
- d)6
Correct answer is option 'D'. Can you explain this answer?
Consider the following directed graph.
The number of different topological orderings of the vertices of the graph is Note : This question was asked as Numerical Answer Type.
a)
1
b)
2
c)
4
d)
6
|
Luminary Institute answered |
Following are different 6 Topological Sortings
a-b-c-d-e-f
a-d-e-b-c-f
a-b-d-c-e-f
a-d-b-c-e-f
a-b-d-e-c-f
a-d-b-e-c-f
a-b-c-d-e-f
a-d-e-b-c-f
a-b-d-c-e-f
a-d-b-c-e-f
a-b-d-e-c-f
a-d-b-e-c-f
A depth-first search is performed on a directed acyclic graph. Let d[u] denote the time at which vertex u is visited for the first time and f[u] the time at which the dfs call to the vertex u terminates. Which of the following statements is always true for all edges (u, v) in the graph ?- a)d[u] < d[v]
- b)d[u] < f[v]
- c)f[u] < f[v]
- d)f[u] > f[v]
Correct answer is option 'D'. Can you explain this answer?
A depth-first search is performed on a directed acyclic graph. Let d[u] denote the time at which vertex u is visited for the first time and f[u] the time at which the dfs call to the vertex u terminates. Which of the following statements is always true for all edges (u, v) in the graph ?
a)
d[u] < d[v]
b)
d[u] < f[v]
c)
f[u] < f[v]
d)
f[u] > f[v]
|
|
Bijoy Iyer answered |
I'm gonna disprove all wrong options here.
A) d[u] < d[v] , Counter Example => Well if we directly start DFS on V first. Then I call DFS on X which visits U.
B) d[u] < f[v] Counter example => Same as A)
C) f[u] < f[v] Counter example => Same as A) again
So answer is D)
A) d[u] < d[v] , Counter Example => Well if we directly start DFS on V first. Then I call DFS on X which visits U.
B) d[u] < f[v] Counter example => Same as A)
C) f[u] < f[v] Counter example => Same as A) again
So answer is D)
Consider an undirected unweighted graph G. Let a breadth-first traversal of G be done starting from a node r. Let d(r, u) and d(r, v) be the lengths of the shortest paths from r to u and v respectively, in G. lf u is visited before v during the breadth-first traversal, which of the following statements is correct? - a)d(r, u) < d (r, v)
- b)d(r, u) > d(r, v)
- c)d(r, u) <= d (r, v)
- d)None of the above
Correct answer is option 'C'. Can you explain this answer?
Consider an undirected unweighted graph G. Let a breadth-first traversal of G be done starting from a node r. Let d(r, u) and d(r, v) be the lengths of the shortest paths from r to u and v respectively, in G. lf u is visited before v during the breadth-first traversal, which of the following statements is correct?
a)
d(r, u) < d (r, v)
b)
d(r, u) > d(r, v)
c)
d(r, u) <= d (r, v)
d)
None of the above
|
|
Ravi Singh answered |
d(r, u) and d(r, v) will be equal when u and v are at same level, otherwise d(r, u) will be less than d(r, v)
Suppose depth first search is executed on the graph below starting at some unknown vertex. Assume that a recursive call to visit a vertex is made only after first checking that the vertex has not been visited earlier. Then the maximum possible recursion depth (including the initial call) is _________.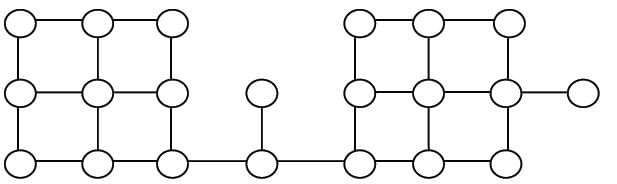
- a)17
- b)18
- c)19
- d)20
Correct answer is option 'C'. Can you explain this answer?
Suppose depth first search is executed on the graph below starting at some unknown vertex. Assume that a recursive call to visit a vertex is made only after first checking that the vertex has not been visited earlier. Then the maximum possible recursion depth (including the initial call) is _________.
a)
17
b)
18
c)
19
d)
20
|
|
Ravi Singh answered |
The following diagram shows the worst case situation where the recursion tree has maximum depth.
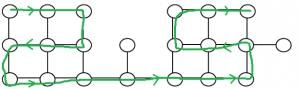
So the recursion depth is 19 (including the first node).
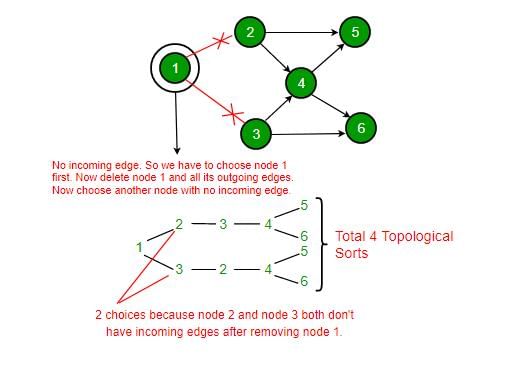
Consider the DAG with Consider V = {1, 2, 3, 4, 5, 6}, shown below. Which of the following is NOT a topological ordering?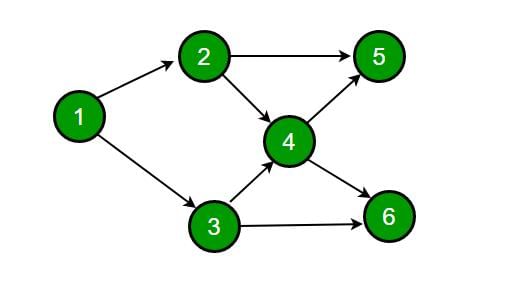
- a)1 2 3 4 5 6
- b)1 3 2 4 5 6
- c)1 3 2 4 6 5
- d)3 2 4 1 6 5
Correct answer is option 'D'. Can you explain this answer?
Consider the DAG with Consider V = {1, 2, 3, 4, 5, 6}, shown below. Which of the following is NOT a topological ordering?
a)
1 2 3 4 5 6
b)
1 3 2 4 5 6
c)
1 3 2 4 6 5
d)
3 2 4 1 6 5
|
|
Cstoppers Instructors answered |
In option D, 1 appears after 2 and 3 which is not possible in Topological Sorting. In the given DAG it is directly visible that there is an outgoing edge from vertex 1 to vertex 2 and 3 hence 2 and 3 cannot come before vertex 1 so clearly option D is incorrect topological sort. But for questions in which it is not directly visible we should know how to find topological sort of a DAG.
Which of the following is an advantage of adjacency list representation over adjacency matrix representation of a graph?- a)In adjacency list representation, space is saved for sparse graphs.
- b)DFS and BSF can be done in O(V + E) time for adjacency list representation. These operations take O(V^2) time in adjacency matrix representation. Here is V and E are number of vertices and edges respectively.
- c)Adding a vertex in adjacency list representation is easier than adjacency matrix representation.
- d)All of the above
Correct answer is option 'D'. Can you explain this answer?
Which of the following is an advantage of adjacency list representation over adjacency matrix representation of a graph?
a)
In adjacency list representation, space is saved for sparse graphs.
b)
DFS and BSF can be done in O(V + E) time for adjacency list representation. These operations take O(V^2) time in adjacency matrix representation. Here is V and E are number of vertices and edges respectively.
c)
Adding a vertex in adjacency list representation is easier than adjacency matrix representation.
d)
All of the above
|
|
Sanya Agarwal answered |
An array of lists is used. The size of the array is equal to the number of vertices. Let the array be an array[]. An entry array[i] represents the list of vertices adjacent to the ith vertex. This representation can also be used to represent a weighted graph. The weights of edges can be represented as lists of pairs.
Breadth First Search (BFS) is started on a binary tree beginning from the root vertex. There is a vertex t at a distance four from the root. If t is the n-th vertex in this BFS traversal, then the maximum possible value of n is _________.
Correct answer is '31'. Can you explain this answer?
Breadth First Search (BFS) is started on a binary tree beginning from the root vertex. There is a vertex t at a distance four from the root. If t is the n-th vertex in this BFS traversal, then the maximum possible value of n is _________.
|
Vaishnavi Dey answered |
Understanding BFS in a Binary Tree
Breadth First Search (BFS) explores nodes level by level, starting from the root. In a binary tree, each node can have up to two children, which leads to an exponential growth in the number of nodes at each level.
Tree Structure
- Level 0 (Root): 1 node
- Level 1: 2 nodes
- Level 2: 4 nodes
- Level 3: 8 nodes
- Level 4: 16 nodes
By the fourth level, the total number of nodes is the sum of all nodes up to that level.
Calculating Total Nodes
- Total nodes from Level 0 to Level 4:
- Level 0: 1
- Level 1: 2
- Level 2: 4
- Level 3: 8
- Level 4: 16
This totals to: 1 + 2 + 4 + 8 + 16 = 31
Position of Vertex t
- Since vertex t is at distance four from the root, it resides on Level 4.
- In BFS, all nodes at Level 4 will be explored after all nodes at Levels 0, 1, 2, and 3.
- The maximum number of nodes explored before reaching Level 4 is 15 (from Levels 0 to 3).
Maximum Possible Value of n
- Adding the nodes from Level 4 (16 nodes) to the previous total (15 nodes):
- 15 (from Levels 0-3) + 16 (from Level 4) = 31
Thus, the maximum possible value of n, where t is the n-th vertex in the BFS traversal, is 31.
Breadth First Search (BFS) explores nodes level by level, starting from the root. In a binary tree, each node can have up to two children, which leads to an exponential growth in the number of nodes at each level.
Tree Structure
- Level 0 (Root): 1 node
- Level 1: 2 nodes
- Level 2: 4 nodes
- Level 3: 8 nodes
- Level 4: 16 nodes
By the fourth level, the total number of nodes is the sum of all nodes up to that level.
Calculating Total Nodes
- Total nodes from Level 0 to Level 4:
- Level 0: 1
- Level 1: 2
- Level 2: 4
- Level 3: 8
- Level 4: 16
This totals to: 1 + 2 + 4 + 8 + 16 = 31
Position of Vertex t
- Since vertex t is at distance four from the root, it resides on Level 4.
- In BFS, all nodes at Level 4 will be explored after all nodes at Levels 0, 1, 2, and 3.
- The maximum number of nodes explored before reaching Level 4 is 15 (from Levels 0 to 3).
Maximum Possible Value of n
- Adding the nodes from Level 4 (16 nodes) to the previous total (15 nodes):
- 15 (from Levels 0-3) + 16 (from Level 4) = 31
Thus, the maximum possible value of n, where t is the n-th vertex in the BFS traversal, is 31.
The cyclomatic complexity of the flow graph of a program provides- a)an upper bound for the number of tests that must be conducted to ensure that all statements have been executed at most once
- b)a lower bound for the number of tests that must be conducted to ensure that all statements have been executed at most once
- c)an upper bound for the number of tests that must be conducted to ensure that all statements have been executed at least once
- d)a lower bound for the number of tests that must be conducted to ensure that all statements have been executed at least once
Correct answer is option 'C'. Can you explain this answer?
The cyclomatic complexity of the flow graph of a program provides
a)
an upper bound for the number of tests that must be conducted to ensure that all statements have been executed at most once
b)
a lower bound for the number of tests that must be conducted to ensure that all statements have been executed at most once
c)
an upper bound for the number of tests that must be conducted to ensure that all statements have been executed at least once
d)
a lower bound for the number of tests that must be conducted to ensure that all statements have been executed at least once
|
|
Ravi Singh answered |
Option (C) is correct, because the cyclomatic complexity of the flow graph of a program provides an upper bound for the number of tests that must be conducted to ensure that all statements have been executed at least once.
Let S and t be two vertices in a undirected graph G=(V,E) having distinct positive edge weights. Let [X,Y] be a partition of V such that s ∈ X and t ∈ Y . Consider the edge having the minimum weight amongst all those edges that have one vertex in X and one vertex in YThe edge e must definitely belong to:.- a)the minimum weighted spanning tree of G
- b)the weighted shortest path from s to t
- c)each path from s to t
- d)the weighted longest path from s to t
Correct answer is option 'A'. Can you explain this answer?
Let S and t be two vertices in a undirected graph G=(V,E) having distinct positive edge weights. Let [X,Y] be a partition of V such that s ∈ X and t ∈ Y . Consider the edge having the minimum weight amongst all those edges that have one vertex in X and one vertex in Y
The edge e must definitely belong to:.
a)
the minimum weighted spanning tree of G
b)
the weighted shortest path from s to t
c)
each path from s to t
d)
the weighted longest path from s to t
|
|
Arnab Kapoor answered |
For 82a The answer should be Option A because edge 'e' is the lightest safe edge connecting X and Y so the minimum
spanning tree of G must contain 'e' (Greedy and optimal choice).
While B might seem correct but it is not always true. One such case is when G is not connected therefore there might not
be any path between 's' and 't'.
Since the question is about definitely true B is incorrect and A is the only correct option
spanning tree of G must contain 'e' (Greedy and optimal choice).
While B might seem correct but it is not always true. One such case is when G is not connected therefore there might not
be any path between 's' and 't'.
Since the question is about definitely true B is incorrect and A is the only correct option
Lets say AC =1 CD = 2 BD = 3 and AB=4
Then if s= A and t= B then AC is the lightest edge crossing X and Y where X = { A } and Y = { C, B, D}
But clearly AC is not on the shortest path from A to B. The shortest path is AB = 4.
But clearly AC is not on the shortest path from A to B. The shortest path is AB = 4.
The degree sequence of a simple graph is the sequence of the degrees of the nodes in the graph in decreasing order. Which of the following sequences can not be the degree sequence of any graph?
I. 7, 6, 5, 4, 4, 3, 2, 1
II. 6, 6, 6, 6, 3, 3, 2, 2
III. 7, 6, 6, 4, 4, 3, 2, 2
IV. 8, 7, 7, 6, 4, 2, 1, 1 - a)I and II
- b)III and IV
- c)IV only
- d)II and IV
Correct answer is option 'D'. Can you explain this answer?
The degree sequence of a simple graph is the sequence of the degrees of the nodes in the graph in decreasing order. Which of the following sequences can not be the degree sequence of any graph?
I. 7, 6, 5, 4, 4, 3, 2, 1
II. 6, 6, 6, 6, 3, 3, 2, 2
III. 7, 6, 6, 4, 4, 3, 2, 2
IV. 8, 7, 7, 6, 4, 2, 1, 1
I. 7, 6, 5, 4, 4, 3, 2, 1
II. 6, 6, 6, 6, 3, 3, 2, 2
III. 7, 6, 6, 4, 4, 3, 2, 2
IV. 8, 7, 7, 6, 4, 2, 1, 1
a)
I and II
b)
III and IV
c)
IV only
d)
II and IV
|
|
Sanya Agarwal answered |
In sequence IV, we have a vertex with degree 8 which is not possible in a simple graph (no self loops and no multiple edges) with total vertex count as 8. Maximum possible degree in such a graph is 7.
In sequence II, four vertices are connected to 6 other vertices, but remaining 4 vertices have degrees as 3, 3, 2 and 2 which are not possible in a simple graph (no self loops and no multiple edges).
Let G be a graph with n vertices and m edges. What is the tightest upper bound on the running time on Depth First Search of G? Assume that the graph is represented using adjacency matrix.- a)O(n)
- b)O(m+n)
- c)O(n2)
- d)O(mn)
Correct answer is option 'C'. Can you explain this answer?
Let G be a graph with n vertices and m edges. What is the tightest upper bound on the running time on Depth First Search of G? Assume that the graph is represented using adjacency matrix.
a)
O(n)
b)
O(m+n)
c)
O(n2)
d)
O(mn)
|
Anirban Khanna answered |
Depth First Search of a graph takes O(m+n) time when the graph is represented using adjacency list.
In adjacency matrix representation, graph is represented as an “n x n” matrix. To do DFS, for every vertex, we traverse the row corresponding to that vertex to find all adjacent vertices (In adjacency list representation we traverse only the adjacent vertices of the vertex). Therefore time complexity becomes O(n2)
For which of the following combinations of the degrees of vertices would the connected graph be eulerian?- a)1,2,3
- b)2,3,4
- c)2,4,5
- d)1,3,5
Correct answer is option 'A'. Can you explain this answer?
For which of the following combinations of the degrees of vertices would the connected graph be eulerian?
a)
1,2,3
b)
2,3,4
c)
2,4,5
d)
1,3,5
|
Sagnik Singh answered |
A graph is eulerian if either all of its vertices are even or if only two of its vertices are odd.
Is following statement true/false? A DFS of a directed graph always produces the same number of tree edges, i.e., independent of the order in which vertices are considered for DFS.- a)True
- b)False
Correct answer is option 'B'. Can you explain this answer?
Is following statement true/false? A DFS of a directed graph always produces the same number of tree edges, i.e., independent of the order in which vertices are considered for DFS.
a)
True
b)
False
|
|
Sanya Agarwal answered |
Consider the following graph. If we start from 'a', then there is one tree edge. If we start from 'b', then there is no tree edge. a→b
Let T be a depth first search tree in an undirected graph G. Vertices u and ν are leaves of this tree T. The degrees of both u and ν in G are at least 2. which one of the following statements is true?- a)There must exist a vertex w adjacent to both u and ν in G
- b)There must exist a vertex w whose removal disconnects u and ν in G
- c)There must exist a cycle in G containing u and ν
- d)There must exist a cycle in G containing u and all its neighbours in G
Correct answer is option 'D'. Can you explain this answer?
Let T be a depth first search tree in an undirected graph G. Vertices u and ν are leaves of this tree T. The degrees of both u and ν in G are at least 2. which one of the following statements is true?
a)
There must exist a vertex w adjacent to both u and ν in G
b)
There must exist a vertex w whose removal disconnects u and ν in G
c)
There must exist a cycle in G containing u and ν
d)
There must exist a cycle in G containing u and all its neighbours in G
|
|
Sagnik Singh answered |
Consider following graph
Dfs is .
so D is answer.
so D is answer.
Suppose we run Dijkstra’s single source shortest-path algorithm on the following edge-weighted directed graph with vertex P as the source.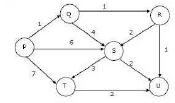
In what order do the nodes get included into the set of vertices for which the shortest path distances are finalized?- a)P,Q,R,S,T,U
- b)P,Q,R,U,S,T
- c)P,Q,R,U,T,S
- d)P,Q,T,R,U,S
Correct answer is option 'B'. Can you explain this answer?
Suppose we run Dijkstra’s single source shortest-path algorithm on the following edge-weighted directed graph with vertex P as the source.
In what order do the nodes get included into the set of vertices for which the shortest path distances are finalized?
a)
P,Q,R,S,T,U
b)
P,Q,R,U,S,T
c)
P,Q,R,U,T,S
d)
P,Q,T,R,U,S
|
|
Sagnik Singh answered |
In Dijkstra's algorithm at each point we choose the smallest weight edge which starts from any one of the vertices in the shortest path found so far and add it to the shortest path.
Let G1 = (V, E1) and G2 = (V, E2) be connected graphs on the same vertex set V with more than two vertices. If G1 ∩ G2 = (V, E1 ∩ E2 ) is not a connected graph, then the graph G1 ∪ G2 = (V, E1 ∪ E2 )- a)cannot have a cut vertex
- b)must have a cycle
- c)must have a cut-edge (bridge)
- d)Has chromatic number strictly greater than those of G1 and G2
Correct answer is option 'B'. Can you explain this answer?
Let G1 = (V, E1) and G2 = (V, E2) be connected graphs on the same vertex set V with more than two vertices. If G1 ∩ G2 = (V, E1 ∩ E2 ) is not a connected graph, then the graph G1 ∪ G2 = (V, E1 ∪ E2 )
a)
cannot have a cut vertex
b)
must have a cycle
c)
must have a cut-edge (bridge)
d)
Has chromatic number strictly greater than those of G1 and G2
|
|
Abhay Ghoshal answered |
Take a tree for example
(A) False. Every vertex of tree(other than leaves) is a cut vertex
(B)True
(C)False. Without E in G1 and G2, G1 U G2 has no bridge.
(D)False. G1 U G2, G1, G2 three graphs have same chromatic number of 2.
(B)True
(C)False. Without E in G1 and G2, G1 U G2 has no bridge.
(D)False. G1 U G2, G1, G2 three graphs have same chromatic number of 2.
Consider the following graph,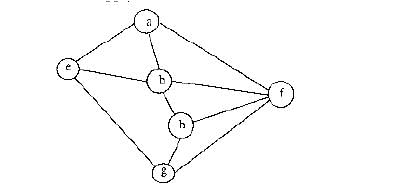
Among the following sequences:
(I) a b e g h f
(II) a b f e h g
(III) a b f h g e
(IV) a f g h b e
Which are depth first traversals of the above graph?- a)I, II and IV only
- b)I and IV only
- c)II, III and IV only
- d)I, III and IV only
Correct answer is option 'D'. Can you explain this answer?
Consider the following graph,
Among the following sequences:
(I) a b e g h f
(II) a b f e h g
(III) a b f h g e
(IV) a f g h b e
Which are depth first traversals of the above graph?
(I) a b e g h f
(II) a b f e h g
(III) a b f h g e
(IV) a f g h b e
Which are depth first traversals of the above graph?
a)
I, II and IV only
b)
I and IV only
c)
II, III and IV only
d)
I, III and IV only
|
|
Sanya Agarwal answered |
We can check all DFSs for following properties.
In DFS, if a vertex 'v' is visited
after 'u', then one of the following is true.
1) (u, v) is an edge.
u
/ \
v w
/ / \
x y z
In DFS, if a vertex 'v' is visited
after 'u', then one of the following is true.
1) (u, v) is an edge.
u
/ \
v w
/ / \
x y z
2) 'u' is a leaf node.
w
/ \
x v
/ / \
u y z
In DFS, after visiting a node, we first recur for all unvisited children. If there are no unvisited children (u is leaf), then control goes back to parent and parent then visits next unvisited children.
w
/ \
x v
/ / \
u y z
In DFS, after visiting a node, we first recur for all unvisited children. If there are no unvisited children (u is leaf), then control goes back to parent and parent then visits next unvisited children.
Let G = (V,E) be connected undirected edge-weighted graph. The weights of the edges in E are positive and distinct. Consider the following statements:(I) Minimum Spanning Tree of G is always unique.(II) Shortest path between any two vertices of G is always unique.Which of the above statements is/are necessarily true?- a)(I) only
- b)(II) only
- c)both (I) and (II)
- d)neither (I) nor (II)
Correct answer is option 'A'. Can you explain this answer?
Let G = (V,E) be connected undirected edge-weighted graph. The weights of the edges in E are positive and distinct. Consider the following statements:
(I) Minimum Spanning Tree of G is always unique.
(II) Shortest path between any two vertices of G is always unique.
Which of the above statements is/are necessarily true?
a)
(I) only
b)
(II) only
c)
both (I) and (II)
d)
neither (I) nor (II)
|
|
Diya Chauhan answered |
> MST is not unique only when edges are not distinct. Here the edges are distinct. Be careful for the keyword
DISTINCT.
DISTINCT.
> Shortest Path can be different even if the edges are distinct. Example is shown below. Shortest path from A
to C is not unique here.
to C is not unique here.
To implement Dijkstra’s shortest path algorithm on unweighted graphs so that it runs in linear time, the data structure to be used is:- a)Queue
- b)Stack
- c)Heap
- d)B-Tree
Correct answer is option 'A'. Can you explain this answer?
To implement Dijkstra’s shortest path algorithm on unweighted graphs so that it runs in linear time, the data structure to be used is:
a)
Queue
b)
Stack
c)
Heap
d)
B-Tree
|
|
Anisha Chavan answered |
Understanding Dijkstra's Algorithm for Unweighted Graphs
Dijkstra's algorithm is typically used to find the shortest paths from a source vertex to all other vertices in a weighted graph. However, when applied to unweighted graphs, it can be optimized to run in linear time using the right data structure.
Why a Queue is the Correct Choice
- Unweighted Graphs: In unweighted graphs, all edges have the same weight (considered as 1). Hence, the primary concern is not the weight but rather the number of edges traversed.
- Breadth-First Search (BFS) Relation: Dijkstra's algorithm, when applied to unweighted graphs, behaves similarly to Breadth-First Search (BFS). BFS explores nodes layer by layer, ensuring that all nodes at the current depth are processed before moving deeper.
- Using a Queue: A queue supports the FIFO (First-In-First-Out) principle, making it an ideal structure for BFS. By using a queue:
- Each vertex is processed in the order it is discovered.
- All adjacent vertices are enqueued for future processing, maintaining the correct order of exploration.
Efficiency in Implementation
- Linear Time Complexity: By using a queue, the algorithm can efficiently explore all vertices, ensuring that every vertex is processed only once. This results in a time complexity of O(V + E), where V is the number of vertices and E is the number of edges, which is linear in terms of the size of the graph.
- Comparison with Other Structures:
- A stack (option B) would lead to a depth-first approach, which is not suited for finding the shortest path in unweighted graphs.
- A heap (option C) is more useful in weighted graphs for efficiently retrieving the minimum distance node.
- A B-tree (option D) is unnecessary for this context as it is typically used for database and file storage.
In summary, for unweighted graphs, using a queue allows Dijkstra's algorithm to run efficiently in linear time, making it the optimal choice for this scenario.
Dijkstra's algorithm is typically used to find the shortest paths from a source vertex to all other vertices in a weighted graph. However, when applied to unweighted graphs, it can be optimized to run in linear time using the right data structure.
Why a Queue is the Correct Choice
- Unweighted Graphs: In unweighted graphs, all edges have the same weight (considered as 1). Hence, the primary concern is not the weight but rather the number of edges traversed.
- Breadth-First Search (BFS) Relation: Dijkstra's algorithm, when applied to unweighted graphs, behaves similarly to Breadth-First Search (BFS). BFS explores nodes layer by layer, ensuring that all nodes at the current depth are processed before moving deeper.
- Using a Queue: A queue supports the FIFO (First-In-First-Out) principle, making it an ideal structure for BFS. By using a queue:
- Each vertex is processed in the order it is discovered.
- All adjacent vertices are enqueued for future processing, maintaining the correct order of exploration.
Efficiency in Implementation
- Linear Time Complexity: By using a queue, the algorithm can efficiently explore all vertices, ensuring that every vertex is processed only once. This results in a time complexity of O(V + E), where V is the number of vertices and E is the number of edges, which is linear in terms of the size of the graph.
- Comparison with Other Structures:
- A stack (option B) would lead to a depth-first approach, which is not suited for finding the shortest path in unweighted graphs.
- A heap (option C) is more useful in weighted graphs for efficiently retrieving the minimum distance node.
- A B-tree (option D) is unnecessary for this context as it is typically used for database and file storage.
In summary, for unweighted graphs, using a queue allows Dijkstra's algorithm to run efficiently in linear time, making it the optimal choice for this scenario.
Consider an undirected random graph of eight vertices. The probability that there is an edge between a pair of vertices is 1/2. What is the expected number of unordered cycles of length three?- a)1/8
- b)1
- c)7
- d)8
Correct answer is option 'C'. Can you explain this answer?
Consider an undirected random graph of eight vertices. The probability that there is an edge between a pair of vertices is 1/2. What is the expected number of unordered cycles of length three?
a)
1/8
b)
1
c)
7
d)
8
|
|
Sanya Agarwal answered |
A cycle of length 3 can be formed with 3 vertices. There can be total 8C3 ways to pick 3 vertices from 8. The probability that there is an edge between two vertices is 1/2. So expected number of unordered cycles of length 3 = (8C3)*(1/2)^3 = 7
For the undirected, weighted graph given below, which of the following sequences of edges represents a correct execution of Prim's algorithm to construct a Minimum Spanning Tree?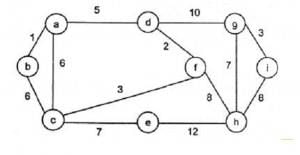
- a)(a, b), (d, f), (f, c), (g, i), (d, a), (g, h), (c, e), (f, h)
- b)(c, e), (c, f), (f, d), (d, a), (a, b), (g, h), (h, f), (g, i)
- c)(d, f), (f, c), (d, a), (a, b), (c, e), (f, h), (g, h), (g, i)
- d)(h, g), (g, i), (h, f), (f, c), (f, d), (d, a), (a, b), (c, e)
Correct answer is option 'C'. Can you explain this answer?
For the undirected, weighted graph given below, which of the following sequences of edges represents a correct execution of Prim's algorithm to construct a Minimum Spanning Tree?
a)
(a, b), (d, f), (f, c), (g, i), (d, a), (g, h), (c, e), (f, h)
b)
(c, e), (c, f), (f, d), (d, a), (a, b), (g, h), (h, f), (g, i)
c)
(d, f), (f, c), (d, a), (a, b), (c, e), (f, h), (g, h), (g, i)
d)
(h, g), (g, i), (h, f), (f, c), (f, d), (d, a), (a, b), (c, e)
|
|
Sanya Agarwal answered |
In prims algorithm we start with any node and keep on exploring minimum cost neighbors of nodes already covered.
Let G be a graph with n vertices and m edges. What is the tightest upper bound on the running time on Depth First Search of G? Assume that the graph is represented using adjacency matrix.- a)O(n)
- b)O(m+n)
- c)O(n2)
- d)O(mn)
Correct answer is option 'C'. Can you explain this answer?
Let G be a graph with n vertices and m edges. What is the tightest upper bound on the running time on Depth First Search of G? Assume that the graph is represented using adjacency matrix.
a)
O(n)
b)
O(m+n)
c)
O(n2)
d)
O(mn)
|
|
Sanya Agarwal answered |
Depth First Search of a graph takes O(m+n) time when the graph is represented using adjacency list. In adjacency matrix representation, graph is represented as an "n x n" matrix. To do DFS, for every vertex, we traverse the row corresponding to that vertex to find all adjacent vertices (In adjacency list representation we traverse only the adjacent vertices of the vertex). Therefore time complexity becomes O(n2)
The most efficient algorithm for finding the number of connected components in an undirected graph on n vertices and m edges has time complexity. (A) θ(n) (B) θ(m) (C) θ(m + n) (D) θ(mn)- a)A
- b)B
- c)C
- d)D
Correct answer is option 'C'. Can you explain this answer?
The most efficient algorithm for finding the number of connected components in an undirected graph on n vertices and m edges has time complexity. (A) θ(n) (B) θ(m) (C) θ(m + n) (D) θ(mn)
a)
A
b)
B
c)
C
d)
D
|
|
Ravi Singh answered |
Connected components can be found in O(m + n) using Tarjan's algorithm. Once we have connected components, we can count them.
Consider the directed graph shown in the figure below. There are multiple shortest paths between vertices and . Which one will be reported by Dijkstra’s shortest path algorithm? Assume that, in any iteration, the shortest path to a vertex is updated only when a strictly shorter path to is discovered.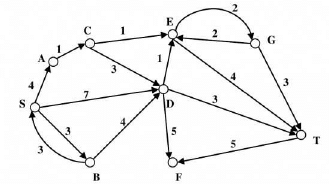
- a) SDT
- b) SBDT
- c) SACDT
- d) SACET
Correct answer is option 'D'. Can you explain this answer?
Consider the directed graph shown in the figure below. There are multiple shortest paths between vertices and . Which one will be reported by Dijkstra’s shortest path algorithm? Assume that, in any iteration, the shortest path to a vertex is updated only when a strictly shorter path to is discovered.
a)
SDT
b)
SBDT
c)
SACDT
d)
SACET
|
Rahul Chatterjee answered |
When the algorithm reaches vertex ‘C’, the distance values of ‘D’ and ‘E’ would be 7 and 6 respectively. So the next picked vertex would be ‘E’
In an adjacency list representation of an undirected simple graph G = (V,E) , each edge (u,v) has two adjacency list entries: [v] in the adjacency list of u , and [u] in the adjacency list of v. These are called twins of each other. A twin pointer is a pointer from an adjacency list entry to its twin. If 
, and the memory size is not a constraint, what is the time complexity of the most efficient algorithm to set the twin pointer in each entry in each adjacency list?- a)
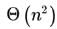
- b)
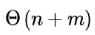
- c)
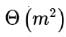
- d)
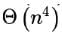
Correct answer is option 'B'. Can you explain this answer?
In an adjacency list representation of an undirected simple graph G = (V,E) , each edge (u,v) has two adjacency list entries: [v] in the adjacency list of u , and [u] in the adjacency list of v. These are called twins of each other. A twin pointer is a pointer from an adjacency list entry to its twin. If 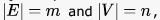, and the memory size is not a constraint, what is the time complexity of the most efficient algorithm to set the twin pointer in each entry in each adjacency list?
, and the memory size is not a constraint, what is the time complexity of the most efficient algorithm to set the twin pointer in each entry in each adjacency list?a)
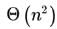
b)
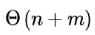
c)
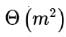
d)
|
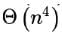
Anshu Mehta answered |
Applying BFS on Undirected graph give you twin pointer .Visit every vertex level-wise for every vertex fill adjacent vertex in the adjacency list. BFS take 0(m+n) time.
take extra field for storing no. of linked list for perticular vertex. take extra m+n time( m vertex and n edges).
So B is answer
So B is answer
We are given 9 tasks 
The execution of each task requires one unit of time. We can execute one task at a time. Each task Ti has a profit Pi and a deadline di . Profit Pi is earned if the task is completed before the end of the dith unit of time.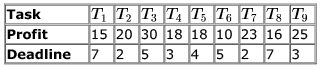 
What is the maximum profit earned?- a)147
- b)165
- c)167
- d)175
Correct answer is option 'A'. Can you explain this answer?
We are given 9 tasks The execution of each task requires one unit of time. We can execute one task at a time. Each task Ti has a profit Pi and a deadline di . Profit Pi is earned if the task is completed before the end of the dith unit of time.
The execution of each task requires one unit of time. We can execute one task at a time. Each task Ti has a profit Pi and a deadline di . Profit Pi is earned if the task is completed before the end of the dith unit of time. What is the maximum profit earned?
a)
147
b)
165
c)
167
d)
175
|
|
Anshu Mehta answered |
The most important statement in question is
each task requires one unit of time
This shows that we can greedily choose the better task and that should give us the optimal solution. The best task would be the one with maximum profit. Thus we can sort the tasks based on deadline and then profit as follows:
0 --T7 -- 1 -- T2 -- 2 -- T9 -- 3 -- T5 -- 4 -- T3 -- 5 -- T8 -- 6 -- T1 -- 7
so we know that T4 and T6 are left
so profit will not include T4 and T6 = 15 + 20 +30 +18 + 16 + 23 + 25 = 147
so profit will not include T4 and T6 = 15 + 20 +30 +18 + 16 + 23 + 25 = 147
Consider a weighted undirected graph with positive edge weights and let be an edge in the graph. It is known that the shortest path from the source vertex to has weight 53 and the shortest path from to has weight 65. Which one of the following statements is always true?- a)
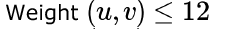
- b)
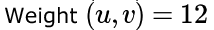
- c)
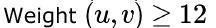
- d)
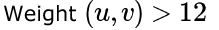
Correct answer is option 'C'. Can you explain this answer?
Consider a weighted undirected graph with positive edge weights and let be an edge in the graph. It is known that the shortest path from the source vertex to has weight 53 and the shortest path from to has weight 65. Which one of the following statements is always true?
a)
b)
c)
d)
|
|
Palak Khanna answered |
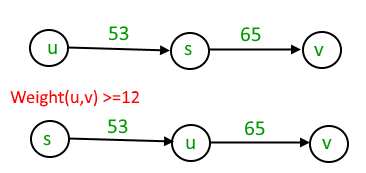
The minimum weight happens when (S,U) + (U,V) = (S,V)
Else (S,U) + (U,V) >= (S,V)
Given (S,U) = 53, (S,V) = 65
53 + (U,V) >= 63
(U,V) >= 12.
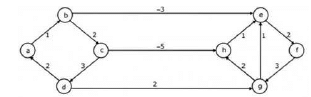Dijkstra's single source shortest path algorithm when run from vertex in the above graph, computes the correct shortest path distance to- a)only vertex a
- b)only vertices a,e,f,g,h
- c)only vertices a,b,c,d
- d)all the vertices
Correct answer is option 'D'. Can you explain this answer?
Dijkstra's single source shortest path algorithm when run from vertex in the above graph, computes the correct shortest path distance to
a)
only vertex a
b)
only vertices a,e,f,g,h
c)
only vertices a,b,c,d
d)
all the vertices
|
|
Roshni Kumar answered |
(d) all the vertices. Just simulate the Dijkstra's algorithm on it. Dijkstra's algorithm is not meant for graphs with negative edge- weight-cycle, but here it does give the correct shortest path.
What is the time complexity of Bellman-Ford single-source shortest path algorithm on a complete graph of n vertices?- a)
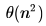
- b)
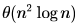
- c)
- d)
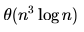
Correct answer is option 'C'. Can you explain this answer?
What is the time complexity of Bellman-Ford single-source shortest path algorithm on a complete graph of n vertices?
a)
b)
c)
d)
|
Akshay Singh answered |
Time complexity of Bellman-Ford algorithm is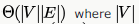 
is number of vertices and 
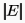is number of edges. If the graph is complete, the value of 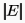becomes 
So overall time complexity becomes 
And given here is n vertices. So answers ends up to 
is number of vertices and is number of edges. If the graph is complete, the value of becomes So overall time complexity becomes 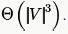And given here is n vertices. So answers ends up to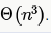 The Breadth First Search algorithm has been implemented using the queue data structure. One possible order of visiting the nodes of the following graph is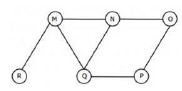
- a)MNOPQR
- b)NQMPOR
- c)QMNPRO
- d)QMNPOR
Correct answer is option 'C'. Can you explain this answer?
The Breadth First Search algorithm has been implemented using the queue data structure. One possible order of visiting the nodes of the following graph is
a)
MNOPQR
b)
NQMPOR
c)
QMNPRO
d)
QMNPOR
|
|
Arnab Kapoor answered |
A) MNOPQR -> If you try to run BFS, after M, you must traverse NQR (In some order) Here P is traversed before Q, which
is wrong.
B) NQMPOR -> This is also not BFS. P is traversed before O !
C) QMNPRO -> Correct
D) QMNPOR -> Incorrect. Because R need to be traversed before O.(Because M is ahead of N in queue.
Answer :- > C
is wrong.
B) NQMPOR -> This is also not BFS. P is traversed before O !
C) QMNPRO -> Correct
D) QMNPOR -> Incorrect. Because R need to be traversed before O.(Because M is ahead of N in queue.
Answer :- > C
Chapter doubts & questions for Graph Based Algorithms - Algorithms 2025 is part of Computer Science Engineering (CSE) exam preparation. The chapters have been prepared according to the Computer Science Engineering (CSE) exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for Computer Science Engineering (CSE) 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Graph Based Algorithms - Algorithms in English & Hindi are available as part of Computer Science Engineering (CSE) exam.
Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free.
Algorithms
81 videos|113 docs|34 tests
|
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup