All Exams >
SSC CGL >
General Intelligence and Reasoning for SSC CGL >
All Questions
All questions of Clock & Calender for SSC CGL Exam
Find the leap year?
- a)700
- b)2000
- c)900
- d)1000
Correct answer is option 'B'. Can you explain this answer?
a)
700
b)
2000
c)
900
d)
1000
|
|
Arun Sharma answered |
Remember the leap year rule:
- Every year divisible by 4 is a leap year, if it is not a century.
- Every 4th century is a leap year, but no other century is a leap year.
- 800,1200 and 2000 comes in the category of 4th century (such as 400,800,1200,1600,2000 etc).
Hence, 800,1200 and 2000 are leap years.
The century can end with
- a)Sunday
- b)Saturday
- c)Thursday
- d)Tuesday
Correct answer is option 'A'. Can you explain this answer?
a)
Sunday
b)
Saturday
c)
Thursday
d)
Tuesday

|
Dhruv Mehra answered |
100 years contain 5 odd days.
Last day of 1st century is Friday.
200 years contain (5 x 2) 3 odd days.
Last day of 2nd century is Wednesday.
300 years contain (5 x 3) = 15 1 odd day.
Last day of 3rd century is Monday.
400 years contain 0 odd day.
Last day of 4th century is Sunday.
This cycle is repeated.
Last day of a century cannot be Tuesday or Thursday or Saturday.
hence,sunday is left only
hence,sunday is left only
.
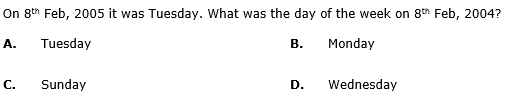
- a)A
- b)B
- c)C
- d)D
Correct answer is option 'C'. Can you explain this answer?
a)
A
b)
B
c)
C
d)
D
|
|
Rohit Jain answered |
The year 2004 is a leap year. It has 2 odd days.
∴ The day on 8th Feb, 2004 is 2 days before the day on 8th Feb, 2005.
Hence, this day is Sunday.
∴ The day on 8th Feb, 2004 is 2 days before the day on 8th Feb, 2005.
Hence, this day is Sunday.
what was the day of Aug15 1955?
- a)Sunday
- b)Monday
- c)Tuesday
- d)Friday
Correct answer is option 'B'. Can you explain this answer?
a)
Sunday
b)
Monday
c)
Tuesday
d)
Friday

|
Dhruv Mehra answered |
Date Facts:
August 15, 1955 was a Monday
Zodiac Sign for this date is: Leo
This date was 22,955 days ago
August 15th 2018 is on a Wednesday
Someone born on this date is 62 years old
What was the day of the Week on 17th June 1998?
- a)Monday
- b)Tuesday
- c)Wednesday
- d)Thursday
Correct answer is option 'C'. Can you explain this answer?
a)
Monday
b)
Tuesday
c)
Wednesday
d)
Thursday
|
|
Arun Sharma answered |
17th June, 1998 = (1997 years + Period from 1.1.1998 to 17.6.1998)
Odd days in 1600 years = 0
Odd days in 300 years = (5 x 3) ≡ 1
97 years has 24 leap years + 73 ordinary years.
Number of odd days in 97 years ( 24 x 2 + 73) = 121 = 2 odd days.
Jan. Feb. March April May June
(31 + 28 + 31 + 30 + 31 + 17) = 168 days
Therefore 168 days = 24 weeks = 0 odd day.
Total number of odd days = (0 + 1 + 2 + 0) = 3.
Given day is Wednesday.
Odd days in 1600 years = 0
Odd days in 300 years = (5 x 3) ≡ 1
97 years has 24 leap years + 73 ordinary years.
Number of odd days in 97 years ( 24 x 2 + 73) = 121 = 2 odd days.
Jan. Feb. March April May June
(31 + 28 + 31 + 30 + 31 + 17) = 168 days
Therefore 168 days = 24 weeks = 0 odd day.
Total number of odd days = (0 + 1 + 2 + 0) = 3.
Given day is Wednesday.
.
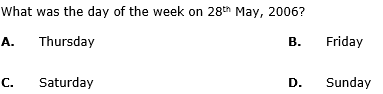
- a)A
- b)B
- c)C
- d)D
Correct answer is option 'D'. Can you explain this answer?
a)
A
b)
B
c)
C
d)
D

|
Aadhar Academy answered |
28 May, 2006 = (2005 years + Period from 1.1.2006 to 28.5.2006)
Odd days in 1600 years = 0
Odd days in 400 years = 0
5 years = (4 ordinary years + 1 leap year) = (4 x 1 + 1 x 2) ≡ 6 odd days
Jan. Feb. March April May
(31 + 28 + 31 + 30 + 28 ) = 148 days
∴ 148 days = (21 weeks + 1 day) ≡ 1 odd day.
Total number of odd days = (0 + 0 + 6 + 1) = 7 ≡ 0 odd day.
Given day is Sunday.
Odd days in 1600 years = 0
Odd days in 400 years = 0
5 years = (4 ordinary years + 1 leap year) = (4 x 1 + 1 x 2) ≡ 6 odd days
Jan. Feb. March April May
(31 + 28 + 31 + 30 + 28 ) = 148 days
∴ 148 days = (21 weeks + 1 day) ≡ 1 odd day.
Total number of odd days = (0 + 0 + 6 + 1) = 7 ≡ 0 odd day.
Given day is Sunday.
.
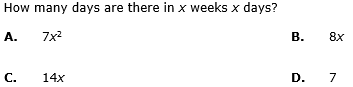
- a)A
- b)B
- c)C
- d)D
Correct answer is option 'B'. Can you explain this answer?
a)
A
b)
B
c)
C
d)
D
|
|
Amit Sharma answered |
x weeks x days = (7x + x) days
= 8x days.
= 8x days.
What will be the day of the week 15th August 2010?- a)Sunday
- b)Monday
- c)Tuesday
- d)Friday
Correct answer is option 'A'. Can you explain this answer?
What will be the day of the week 15th August 2010?
a)
Sunday
b)
Monday
c)
Tuesday
d)
Friday

|
Priyanka Menon answered |
**Explanation:**
To determine the day of the week for a given date, we can use the concept of the Gregorian calendar and some basic calculations.
**Step 1: Determining the Reference Day**
- To find the day of the week for a specific date, we need to determine a reference day. In this case, we can choose a known day and its corresponding date that falls within the same year as the given date. Let's choose the reference day as January 1, 2010, which was a Friday.
**Step 2: Counting the Number of Days**
- The next step is to count the number of days between the reference day and the given date. For this, we need to consider both the number of days within the same year and the number of days in the intervening years.
- From January 1, 2010, to August 15, 2010, there are 226 days.
- Additionally, we need to consider the number of days in the intervening years (2011-2019) between the reference year and the given year. There are 9 years, and each year has 365 days, so the total number of intervening days is 9 * 365 = 3285.
- Therefore, the total number of days between the reference day and August 15, 2010, is 226 + 3285 = 3511.
**Step 3: Determining the Day of the Week**
- Now, we need to find the remainder when the total number of days is divided by 7. This remainder will give us the day of the week.
- 3511 divided by 7 equals 501 remainder 4.
- Since the reference day was Friday (which corresponds to 0), we can count 4 days forward to determine the day of the week for August 15, 2010.
- Friday (0) -> Saturday (1) -> Sunday (2) -> Monday (3) -> **Tuesday (4)**.
Therefore, the day of the week for August 15, 2010, was **Tuesday**.
To determine the day of the week for a given date, we can use the concept of the Gregorian calendar and some basic calculations.
**Step 1: Determining the Reference Day**
- To find the day of the week for a specific date, we need to determine a reference day. In this case, we can choose a known day and its corresponding date that falls within the same year as the given date. Let's choose the reference day as January 1, 2010, which was a Friday.
**Step 2: Counting the Number of Days**
- The next step is to count the number of days between the reference day and the given date. For this, we need to consider both the number of days within the same year and the number of days in the intervening years.
- From January 1, 2010, to August 15, 2010, there are 226 days.
- Additionally, we need to consider the number of days in the intervening years (2011-2019) between the reference year and the given year. There are 9 years, and each year has 365 days, so the total number of intervening days is 9 * 365 = 3285.
- Therefore, the total number of days between the reference day and August 15, 2010, is 226 + 3285 = 3511.
**Step 3: Determining the Day of the Week**
- Now, we need to find the remainder when the total number of days is divided by 7. This remainder will give us the day of the week.
- 3511 divided by 7 equals 501 remainder 4.
- Since the reference day was Friday (which corresponds to 0), we can count 4 days forward to determine the day of the week for August 15, 2010.
- Friday (0) -> Saturday (1) -> Sunday (2) -> Monday (3) -> **Tuesday (4)**.
Therefore, the day of the week for August 15, 2010, was **Tuesday**.
16th July 1776,the day of the week was?- a)Wednesday
- b)Tuesday
- c)Saturday
- d)Friday
Correct answer is option 'B'. Can you explain this answer?
16th July 1776,the day of the week was?
a)
Wednesday
b)
Tuesday
c)
Saturday
d)
Friday
|
|
Kiran Reddy answered |
16th July, 1776 = (1775 years + Period from 1st Jan, 1776 to 16th July, 1776)
Counting of odd days :
1600 years have 0 odd day
100 years have 5 odd days
75 years = (18 leap years + 57 ordinary years)
= [(18 x 2) + (57 x 1)]
= 93 (13 weeks + 2 days)
= 2 odd days
1775 years have (0 + 5 + 2) odd days = 7 odd days = 0 odd day
Jan Feb Mar Apr May Jun Jul
31 + 29 + 31 + 30 + 31 + 30 + 16
= 198 days
= (28 weeks + 2 days)
Total number of odd days = (0 + 2) = 2
Required day was 'Tuesday'.
Counting of odd days :
1600 years have 0 odd day
100 years have 5 odd days
75 years = (18 leap years + 57 ordinary years)
= [(18 x 2) + (57 x 1)]
= 93 (13 weeks + 2 days)
= 2 odd days
1775 years have (0 + 5 + 2) odd days = 7 odd days = 0 odd day
Jan Feb Mar Apr May Jun Jul
31 + 29 + 31 + 30 + 31 + 30 + 16
= 198 days
= (28 weeks + 2 days)
Total number of odd days = (0 + 2) = 2
Required day was 'Tuesday'.
which calendar year will be same as the year 2008?- a)2018
- b)2020
- c)1980
- d)1960
Correct answer is option 'C'. Can you explain this answer?
which calendar year will be same as the year 2008?
a)
2018
b)
2020
c)
1980
d)
1960
|
|
Kiran Reddy answered |
For every 28 years, the calendars will same,
so the years 2008,2036 have the same calendar as 1980.
so the years 2008,2036 have the same calendar as 1980.
On what dates of April 2001 did Wednesday fall?
- a)1st, 8th, 15th, 22nd, 29th
- b)2nd,9th, 16th, 23nd, 30th
- c)3rd, 10th, 17th, 24nd
- d)4st,11th, 18th, 25nd
Correct answer is option 'D'. Can you explain this answer?
a)
1st, 8th, 15th, 22nd, 29th
b)
2nd,9th, 16th, 23nd, 30th
c)
3rd, 10th, 17th, 24nd
d)
4st,11th, 18th, 25nd
|
|
Vikram Kapoor answered |
We shall find the day on 1st April, 2001.
1st April, 2001 = (2000 years + Period from 1.1.2001 to 1.4.2001)
Odd days in 1600 years = 0
Odd days in 400 years = 0
Jan. Feb. March April
(31 + 28 + 31 + 1) = 91 days ≡ 0 odd days.
Total number of odd days = (0 + 0 + 0) = 0
On 1st April, 2001 it was Sunday.
In April, 2001 Wednesday falls on 4th, 11th, 18th and 25th
1st April, 2001 = (2000 years + Period from 1.1.2001 to 1.4.2001)
Odd days in 1600 years = 0
Odd days in 400 years = 0
Jan. Feb. March April
(31 + 28 + 31 + 1) = 91 days ≡ 0 odd days.
Total number of odd days = (0 + 0 + 0) = 0
On 1st April, 2001 it was Sunday.
In April, 2001 Wednesday falls on 4th, 11th, 18th and 25th
On what dates of jan 1st 1992 did friday fall?
- a)1st,8th,15th,22nd,29th
- b)2nd,9th,15th,23nd,30th
- c)3rd,10th,16th,22nd,29th
- d)none of the above
Correct answer is option 'A'. Can you explain this answer?
a)
1st,8th,15th,22nd,29th
b)
2nd,9th,15th,23nd,30th
c)
3rd,10th,16th,22nd,29th
d)
none of the above
|
|
Kajal Sengupta answered |
Each day of the week is repeated after 7 days.
So, after 63 days, it will be Monday.
 After 61 days, it will be Saturday.
After 61 days, it will be Saturday.The Republic day of India was celebrated on Friday in year 2008. On which day, it will be celebrated in 2012?- a)Tuesday
- b)Wednesday
- c)Thrusday
- d)Friday
Correct answer is option 'B'. Can you explain this answer?
The Republic day of India was celebrated on Friday in year 2008. On which day, it will be celebrated in 2012?
a)
Tuesday
b)
Wednesday
c)
Thrusday
d)
Friday

|
Ssc Cgl answered |
26th January (Republic day) 2008
→ Friday
Clary, it will be on Wednesday in 2012.
→ Friday
Clary, it will be on Wednesday in 2012.
If 2nd June 2012 is Saturday then which day is 7th July 2012?- a)Tuesday
- b)Wednesday
- c)Thursday
- d)Saturday
Correct answer is option 'D'. Can you explain this answer?
If 2nd June 2012 is Saturday then which day is 7th July 2012?
a)
Tuesday
b)
Wednesday
c)
Thursday
d)
Saturday

|
EduRev SSC CGL answered |
Number of days in June is 30 -2 = 28, and number of days in July is 7, total number of days is 28 + 7 = 35, when we divide 35 by 7 remainder is 0, or number of odd days is 0 hence 7th July must be the same day as that of 2nd June i.e. Saturday in this case.
I was born on August 11. Mohan is younger to me by 11 days. This year's independence day falls on Monday. The day on which Mohan's birthday will fall this year will be
- a)Sunday
- b)Tuesday
- c)Monday
- d)Thursday
Correct answer is option 'A'. Can you explain this answer?
I was born on August 11. Mohan is younger to me by 11 days. This year's independence day falls on Monday. The day on which Mohan's birthday will fall this year will be
a)
Sunday
b)
Tuesday
c)
Monday
d)
Thursday

|
Target Study Academy answered |
Mohan was born on 31st July, August 15 falls on Monday.
Mrs Susheela celebrated her wedding anniversary on Tuesday, 30th September, 1997. When will she celebrate her next wedding anniversary on the same day?- a)30th September, 2003
- b)30th September, 2004
- c)30th September, 2002
- d)30th October, 2003
Correct answer is option 'A'. Can you explain this answer?
Mrs Susheela celebrated her wedding anniversary on Tuesday, 30th September, 1997. When will she celebrate her next wedding anniversary on the same day?
a)
30th September, 2003
b)
30th September, 2004
c)
30th September, 2002
d)
30th October, 2003

|
T.S Academy answered |
Total number of odd days
30 September, 1997-98 = 1
30 September, 1998-99 = 1
30 September, 1999-2000 = 2
30 September, 2000-02 = 1
30 September, 2001-02 = 1
30 September, 2002-03 = 1/7
∴ Tuesday + 7 = Tuesday
So, the next Tuesday will come on the Mrs Susheela's wedding anniversary in 30th September, 2003
30 September, 1997-98 = 1
30 September, 1998-99 = 1
30 September, 1999-2000 = 2
30 September, 2000-02 = 1
30 September, 2001-02 = 1
30 September, 2002-03 = 1/7
∴ Tuesday + 7 = Tuesday
So, the next Tuesday will come on the Mrs Susheela's wedding anniversary in 30th September, 2003
If January 1 is a Friday, what is the first day of the month of March in a leap year?- a)Tuesday
- b)Wednesday
- c)Thursday
- d)Friday
Correct answer is option 'A'. Can you explain this answer?
If January 1 is a Friday, what is the first day of the month of March in a leap year?
a)
Tuesday
b)
Wednesday
c)
Thursday
d)
Friday

|
Iq Funda answered |
Total number of days from January 1 to march 1
= 31 + 29 + 1
= 61 days
(February in leap years = 29 days) = 61 ÷ 7
= 8 weeks and 5 odd days
So, the fifth day from Friday = Tuesday
= 31 + 29 + 1
= 61 days
(February in leap years = 29 days) = 61 ÷ 7
= 8 weeks and 5 odd days
So, the fifth day from Friday = Tuesday
If 15 March 1816 was Friday, what day of the week would 15th April 1916 be?- a)Monday
- b)Saturday
- c)Thursday
- d)Wednesday
Correct answer is option 'B'. Can you explain this answer?
If 15 March 1816 was Friday, what day of the week would 15th April 1916 be?
a)
Monday
b)
Saturday
c)
Thursday
d)
Wednesday

|
Riverdale Learning Institute answered |
We are given that 15th March 1816 was a Friday.
Now we know that 100 years have 5 odd days. So till 15th March 1916, we will be having 5 odd days.
So if we move from 15th March 1816 to 15th March 1916, we will encounter 5 odd days.
Now from 15th March 1916 to 15th April 1916 there would be 3 odd days.
So total number of odd days = 5 + 3 = 8
8 mod 7 = 1
So 15th April 1916 would be Friday + 1 = Saturday
What was the day the 2nd July, 1984?- a)Wednesday
- b)Tuesday
- c)Monday
- d)Thursday
Correct answer is option 'C'. Can you explain this answer?
What was the day the 2nd July, 1984?
a)
Wednesday
b)
Tuesday
c)
Monday
d)
Thursday
|
|
Abhiram Mehra answered |
Day of the Week on 2nd July, 1984
The 2nd of July, 1984 was a Monday.
Explanation:
- To determine the day of the week for a given date in the past, we can use a perpetual calendar or a day of the week calculator.
- In this case, when we input the date 2nd July, 1984 into a day of the week calculator, it confirms that it was a Monday.
- Therefore, the correct answer is option 'c' - Monday.
If 09/12/2001(DD/MM/YYYY) happens to be Sunday, then 09/12/1971 would have been a- a)Wednesday
- b)Thursday
- c)Saturday
- d)Tuesday
Correct answer is option 'B'. Can you explain this answer?
If 09/12/2001(DD/MM/YYYY) happens to be Sunday, then 09/12/1971 would have been a
a)
Wednesday
b)
Thursday
c)
Saturday
d)
Tuesday
|
|
Dhruba Pillai answered |
Explanation:
Given Dates:
09/12/2001 (DD/MM/YYYY) = Sunday
09/12/1971 (DD/MM/YYYY)
Identifying the Day of the Week:
To determine the day of the week for 09/12/1971, we need to consider the number of days between 09/12/1971 and 09/12/2001.
Calculating the Difference:
The difference between 09/12/1971 and 09/12/2001 is 30 years.
Now, we need to consider the number of days in these 30 years, including leap years.
Leap Years:
From 1971 to 2001, there are 7 leap years (1972, 1976, 1980, 1984, 1988, 1992, 1996).
Calculating Total Days:
Number of days = 30 years * 365 days/year + 7 leap years = 10957 days
Day of the Week:
Now, when we divide the total days by 7 (since there are 7 days in a week), the remainder will give us the day of the week for 09/12/1971.
Calculation:
Sunday (09/12/2001) + 10957 days = Thursday
Therefore, if 09/12/2001 was a Sunday, then 09/12/1971 would have been a Thursday.
Find the angle between minute hand and hour hand at 4 : 20 Am- a)10°
- b)12.5°
- c)15°
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Find the angle between minute hand and hour hand at 4 : 20 Am
a)
10°
b)
12.5°
c)
15°
d)
None of these
|
|
Nilesh Banerjee answered |
Understanding the Problem
To find the angle between the hour hand and the minute hand at 4:20, we can use the following approach:
Calculating the Positions of the Hands
1. **Minute Hand Position**:
- The minute hand moves 360 degrees in 60 minutes.
- Thus, in 20 minutes, the minute hand moves:
\[
\text{Minute Angle} = \frac{360}{60} \times 20 = 120 \text{ degrees}
\]
2. **Hour Hand Position**:
- The hour hand moves 360 degrees in 12 hours.
- Therefore, in 4 hours, the hour hand moves:
\[
\text{Hour Angle} = \frac{360}{12} \times 4 = 120 \text{ degrees}
\]
- Additionally, the hour hand moves for the 20 minutes past 4 o'clock:
\[
\text{Additional Angle} = \frac{360}{12 \times 60} \times 20 = 10 \text{ degrees}
\]
- Consequently, the total position of the hour hand at 4:20 is:
\[
\text{Total Hour Angle} = 120 + 10 = 130 \text{ degrees}
\]
Finding the Angle Between the Hands
3. **Angle Between Hour and Minute Hand**:
- The angle between the two hands is calculated by finding the absolute difference:
\[
\text{Angle} = |\text{Hour Angle} - \text{Minute Angle}|
\]
- Substituting the values:
\[
\text{Angle} = |130 - 120| = 10 \text{ degrees}
\]
Conclusion
Thus, the angle between the minute hand and the hour hand at 4:20 is **10 degrees**. Therefore, the correct answer is option 'A'.
To find the angle between the hour hand and the minute hand at 4:20, we can use the following approach:
Calculating the Positions of the Hands
1. **Minute Hand Position**:
- The minute hand moves 360 degrees in 60 minutes.
- Thus, in 20 minutes, the minute hand moves:
\[
\text{Minute Angle} = \frac{360}{60} \times 20 = 120 \text{ degrees}
\]
2. **Hour Hand Position**:
- The hour hand moves 360 degrees in 12 hours.
- Therefore, in 4 hours, the hour hand moves:
\[
\text{Hour Angle} = \frac{360}{12} \times 4 = 120 \text{ degrees}
\]
- Additionally, the hour hand moves for the 20 minutes past 4 o'clock:
\[
\text{Additional Angle} = \frac{360}{12 \times 60} \times 20 = 10 \text{ degrees}
\]
- Consequently, the total position of the hour hand at 4:20 is:
\[
\text{Total Hour Angle} = 120 + 10 = 130 \text{ degrees}
\]
Finding the Angle Between the Hands
3. **Angle Between Hour and Minute Hand**:
- The angle between the two hands is calculated by finding the absolute difference:
\[
\text{Angle} = |\text{Hour Angle} - \text{Minute Angle}|
\]
- Substituting the values:
\[
\text{Angle} = |130 - 120| = 10 \text{ degrees}
\]
Conclusion
Thus, the angle between the minute hand and the hour hand at 4:20 is **10 degrees**. Therefore, the correct answer is option 'A'.
If Republic day was celebrated in 1996 on Friday, on which day in 2000 Independence was celebrated?- a)Tuesday
- b)Monday
- c)Sunday
- d)Saturday
Correct answer is option 'A'. Can you explain this answer?
If Republic day was celebrated in 1996 on Friday, on which day in 2000 Independence was celebrated?
a)
Tuesday
b)
Monday
c)
Sunday
d)
Saturday

|
Target Study Academy answered |
26 January, 1996 to 15 August, 2000 days were = 1663
1663 having odd day = 4
∴ In the year 2000, Independence day will on Tuesday.
1663 having odd day = 4
∴ In the year 2000, Independence day will on Tuesday.
How many Sundays will be in a period of 100 years.- a)5217
- b)5219
- c)5217 or 5218
- d)5218 or 5219
Correct answer is option 'C'. Can you explain this answer?
How many Sundays will be in a period of 100 years.
a)
5217
b)
5219
c)
5217 or 5218
d)
5218 or 5219

|
Malavika Rane answered |
Calculation of the Number of Sundays in a Period of 100 Years:
To determine the number of Sundays in a period of 100 years, we need to consider some key factors:
1. Leap Years:
- A leap year is a year that is evenly divisible by 4, except for end-of-century years, which must be divisible by 400 to be considered a leap year.
- In a leap year, there are 366 days instead of the usual 365 days.
2. Number of Days in a Year:
- In a non-leap year, there are 365 days.
- In a leap year, there are 366 days.
3. Day of the Week:
- A week has 7 days, starting from Sunday and ending on Saturday.
Step 1: Calculate the number of leap years in the given period of 100 years.
- Dividing 100 by 4, we get 25 leap years.
- However, century years (divisible by 100) are not considered leap years unless they are divisible by 400.
- Out of the 25 leap years, 4 of them (1900, 1800, 1700, 1600) are not leap years because they are divisible by 100 but not by 400.
- So, the total number of leap years in the given period is 25 - 4 = 21 leap years.
Step 2: Calculate the number of days in the given period of 100 years.
- In 100 years, there are 100 x 365 = 36,500 days.
- Adding the 21 leap years, we get an additional 21 x 366 = 7,686 days.
- Therefore, the total number of days in the given period is 36,500 + 7,686 = 44,186 days.
Step 3: Calculate the number of Sundays in the given period.
- Since a week has 7 days, the remainder when dividing the total number of days (44,186) by 7 will give us the number of Sundays.
- 44,186 divided by 7 gives a quotient of 6,312 and a remainder of 2.
- This means that there are 6,312 complete weeks and 2 additional days.
- As the first day of the given period is not mentioned, we cannot determine the exact day for the additional 2 days.
- However, if the first day is Sunday, then those 2 additional days will also be Sundays.
- Therefore, the number of Sundays in the given period is 6,312 (complete weeks) + 2 (additional days) = 6,314 Sundays.
Conclusion:
The correct answer is option 'C' (5217 or 5218). The number of Sundays in a period of 100 years can be either 5217 or 5218, depending on the specific days of the week for the first two days of the given period.
To determine the number of Sundays in a period of 100 years, we need to consider some key factors:
1. Leap Years:
- A leap year is a year that is evenly divisible by 4, except for end-of-century years, which must be divisible by 400 to be considered a leap year.
- In a leap year, there are 366 days instead of the usual 365 days.
2. Number of Days in a Year:
- In a non-leap year, there are 365 days.
- In a leap year, there are 366 days.
3. Day of the Week:
- A week has 7 days, starting from Sunday and ending on Saturday.
Step 1: Calculate the number of leap years in the given period of 100 years.
- Dividing 100 by 4, we get 25 leap years.
- However, century years (divisible by 100) are not considered leap years unless they are divisible by 400.
- Out of the 25 leap years, 4 of them (1900, 1800, 1700, 1600) are not leap years because they are divisible by 100 but not by 400.
- So, the total number of leap years in the given period is 25 - 4 = 21 leap years.
Step 2: Calculate the number of days in the given period of 100 years.
- In 100 years, there are 100 x 365 = 36,500 days.
- Adding the 21 leap years, we get an additional 21 x 366 = 7,686 days.
- Therefore, the total number of days in the given period is 36,500 + 7,686 = 44,186 days.
Step 3: Calculate the number of Sundays in the given period.
- Since a week has 7 days, the remainder when dividing the total number of days (44,186) by 7 will give us the number of Sundays.
- 44,186 divided by 7 gives a quotient of 6,312 and a remainder of 2.
- This means that there are 6,312 complete weeks and 2 additional days.
- As the first day of the given period is not mentioned, we cannot determine the exact day for the additional 2 days.
- However, if the first day is Sunday, then those 2 additional days will also be Sundays.
- Therefore, the number of Sundays in the given period is 6,312 (complete weeks) + 2 (additional days) = 6,314 Sundays.
Conclusion:
The correct answer is option 'C' (5217 or 5218). The number of Sundays in a period of 100 years can be either 5217 or 5218, depending on the specific days of the week for the first two days of the given period.
If March 5, 2012 was a Wednesday, what was the day on November 5, 2014?
- a)Tuesday
- b)Friday
- c)Thursday
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If March 5, 2012 was a Wednesday, what was the day on November 5, 2014?
a)
Tuesday
b)
Friday
c)
Thursday
d)
None of these

|
EduRev SSC CGL answered |
Here we have to find the number of odd days between, 5th march and 5th November,
Number of days in March is 26 or 5 odd days
(Here we have not included 5th march)
Number of days in April is 30 or 2 odd days
Number of days in May is 31 or 3 odd days
Number of days in June is 30 or 2 odd days
Number of days in July is 31 or 3 odd days
Number of days in August is 31 or 3 odd days
Number of days in September is 30 or 2 odd days
Number of days in October is 31 or 3 odd days
Number of days in November is 5 or 5 odd days
(Here 5th November is included)
So total number of odd days = 5 + 2 + 3 + 2 + 3 + 3 +2 + 3 + 5 = 28 when divided by 7 gives remainder 0 hence 5th November will be same as that of 5th march.
Number of days in March is 26 or 5 odd days
(Here we have not included 5th march)
Number of days in April is 30 or 2 odd days
Number of days in May is 31 or 3 odd days
Number of days in June is 30 or 2 odd days
Number of days in July is 31 or 3 odd days
Number of days in August is 31 or 3 odd days
Number of days in September is 30 or 2 odd days
Number of days in October is 31 or 3 odd days
Number of days in November is 5 or 5 odd days
(Here 5th November is included)
So total number of odd days = 5 + 2 + 3 + 2 + 3 + 3 +2 + 3 + 5 = 28 when divided by 7 gives remainder 0 hence 5th November will be same as that of 5th march.
Find the percentage change in angle between minute hand hour hand from 2 PM to 6 PM.- a)100
- b)200
- c)250
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
Find the percentage change in angle between minute hand hour hand from 2 PM to 6 PM.
a)
100
b)
200
c)
250
d)
None of these

|
Ssc Cgl answered |
At 2 PM angle between minute hand and hour hand is 60° and that at 6 PM is 180° hence percentage change is 200%.
If 18th February, 1997 falls on Tuesday, then what will be the day on 18th February, 1999?- a)Monday
- b)Tuesday
- c)Thursday
- d)Friday
Correct answer is option 'C'. Can you explain this answer?
If 18th February, 1997 falls on Tuesday, then what will be the day on 18th February, 1999?
a)
Monday
b)
Tuesday
c)
Thursday
d)
Friday

|
Malavika Rane answered |
Understanding the Problem
To determine the day of the week on 18th February 1999, starting from 18th February 1997, we must calculate the number of leap years and regular years between these dates.
Years in Consideration
- 1997: Regular year (365 days)
- 1998: Regular year (365 days)
- 1999: Not included since we are looking for 18th February.
Calculating Total Days
- From 18th February 1997 to 18th February 1998 = 365 days (1997 is a regular year)
- From 18th February 1998 to 18th February 1999 = 365 days (1998 is also a regular year)
Total Days Calculation
- Total Days = 365 + 365 = 730 days
Finding the Day of the Week
- Since 1 week = 7 days, we can find the number of weeks in 730 days:
- 730 ÷ 7 = 104 weeks and 2 days
- This means there are 104 complete weeks and 2 extra days.
Determining the Final Day
- Starting from Tuesday (18th February 1997):
- Add 2 days:
- Wednesday (1 day)
- Thursday (2 days)
Conclusion
Thus, 18th February 1999 will fall on Thursday. Therefore, the correct answer is option C.
To determine the day of the week on 18th February 1999, starting from 18th February 1997, we must calculate the number of leap years and regular years between these dates.
Years in Consideration
- 1997: Regular year (365 days)
- 1998: Regular year (365 days)
- 1999: Not included since we are looking for 18th February.
Calculating Total Days
- From 18th February 1997 to 18th February 1998 = 365 days (1997 is a regular year)
- From 18th February 1998 to 18th February 1999 = 365 days (1998 is also a regular year)
Total Days Calculation
- Total Days = 365 + 365 = 730 days
Finding the Day of the Week
- Since 1 week = 7 days, we can find the number of weeks in 730 days:
- 730 ÷ 7 = 104 weeks and 2 days
- This means there are 104 complete weeks and 2 extra days.
Determining the Final Day
- Starting from Tuesday (18th February 1997):
- Add 2 days:
- Wednesday (1 day)
- Thursday (2 days)
Conclusion
Thus, 18th February 1999 will fall on Thursday. Therefore, the correct answer is option C.
A clock is set right at 5 am. The clock loss 16 min in 24 h. What will be the right time when the clock indicates 10 Pm on the third day?- a)11 : 15 pm
- b)11 : 00 pm
- c)12 : 00 pm
- d)12 : 30 pm
Correct answer is option 'B'. Can you explain this answer?
A clock is set right at 5 am. The clock loss 16 min in 24 h. What will be the right time when the clock indicates 10 Pm on the third day?
a)
11 : 15 pm
b)
11 : 00 pm
c)
12 : 00 pm
d)
12 : 30 pm

|
G.K Academy answered |
Time from 5 am of a particular day to 10 pm on the 4th day is 89 h. Now, the clock loses 16 min in 24 h or on other words, we can say that 23 h 44 min of this clock is equal to 24 h of the correct clock. or (23 + 44/60)
⇒ 356 h of this clock = 24 h of the correct clock
∴ 89 h of this clock
= (24 x 15/356 x 89) h of correct clock
= 90 h of the correct clock
⇒ 356 h of this clock = 24 h of the correct clock
∴ 89 h of this clock
= (24 x 15/356 x 89) h of correct clock
= 90 h of the correct clock
A clock is set at 10 a.m. The clock loses 16 minute in 24 hours. What will be the true time when the clock indicates 3 a.m. on 4th day ?- a)9 p.m
- b)10 p.m
- c)11 p.m
- d)12 p.m
Correct answer is option 'C'. Can you explain this answer?
A clock is set at 10 a.m. The clock loses 16 minute in 24 hours. What will be the true time when the clock indicates 3 a.m. on 4th day ?
a)
9 p.m
b)
10 p.m
c)
11 p.m
d)
12 p.m

|
Iq Funda answered |
Time from 10 a.m on a day to 3 a.m on 4th day = 24 x 3 + 17 = 89 hours.
Now 23 hrs 44 min. of this clock = 24 hours of correct clock.
89 hrs of faulty clock = (24 x 15/356 x 89) hrs = 90 hrs.
So, the correct time is 11 p.m
Now 23 hrs 44 min. of this clock = 24 hours of correct clock.
89 hrs of faulty clock = (24 x 15/356 x 89) hrs = 90 hrs.
So, the correct time is 11 p.m
At what time between 1'O clock and 2'O clock the hands of the clock are opposite to each other.- a)34(6/11) past 1'Oclock
- b)38(2/11)past 1'Oclock
- c)56(8/11)past 1'Oclock
- d)64(9/11)past 1'Oclock
Correct answer is option 'B'. Can you explain this answer?
At what time between 1'O clock and 2'O clock the hands of the clock are opposite to each other.
a)
34(6/11) past 1'Oclock
b)
38(2/11)past 1'Oclock
c)
56(8/11)past 1'Oclock
d)
64(9/11)past 1'Oclock
|
|
Abhiram Mehra answered |
Explanation:
Concept:
When the hands of the clock are opposite to each other, they are 180 degrees apart. To find the exact time when this happens, we need to calculate the angle between the hour and minute hands.
Calculations:
1. Calculate the minute hand's position:
- At 10:00, the minute hand points at 12 and is 0 minutes away.
- Calculate how far the minute hand moves in one minute: 360 degrees / 60 minutes = 6 degrees per minute.
- At 38(2/11) minutes past 10, the minute hand is at: 38(2/11) * 6 = 228 + 12 = 240 degrees.
2. Calculate the hour hand's position:
- At 10:00, the hour hand points at 10 and is 0 minutes away.
- Calculate how far the hour hand moves in one minute: 360 degrees / (12 hours * 60 minutes) = 0.5 degrees per minute.
- At 38(2/11) minutes past 10, the hour hand is at: 38(2/11) * 0.5 = 19 + 10 = 29 degrees.
3. Calculate the angle between the hour and minute hands:
- The angle between the hour and minute hands is: |240 - 29| = 211 degrees.
4. Verify if the hands are opposite:
- Since 211 degrees is less than 180 degrees, the hands are not opposite at 38(2/11) past 10.
Therefore, the correct answer is option B. 38(2/11) past 10 o'clock.
Concept:
When the hands of the clock are opposite to each other, they are 180 degrees apart. To find the exact time when this happens, we need to calculate the angle between the hour and minute hands.
Calculations:
1. Calculate the minute hand's position:
- At 10:00, the minute hand points at 12 and is 0 minutes away.
- Calculate how far the minute hand moves in one minute: 360 degrees / 60 minutes = 6 degrees per minute.
- At 38(2/11) minutes past 10, the minute hand is at: 38(2/11) * 6 = 228 + 12 = 240 degrees.
2. Calculate the hour hand's position:
- At 10:00, the hour hand points at 10 and is 0 minutes away.
- Calculate how far the hour hand moves in one minute: 360 degrees / (12 hours * 60 minutes) = 0.5 degrees per minute.
- At 38(2/11) minutes past 10, the hour hand is at: 38(2/11) * 0.5 = 19 + 10 = 29 degrees.
3. Calculate the angle between the hour and minute hands:
- The angle between the hour and minute hands is: |240 - 29| = 211 degrees.
4. Verify if the hands are opposite:
- Since 211 degrees is less than 180 degrees, the hands are not opposite at 38(2/11) past 10.
Therefore, the correct answer is option B. 38(2/11) past 10 o'clock.
If it was Saturday on December 17, 1899, what will be the day on December 22,1901?- a)Friday
- b)Saturday
- c)Sunday
- d)Monday
Correct answer is option 'B'. Can you explain this answer?
If it was Saturday on December 17, 1899, what will be the day on December 22,1901?
a)
Friday
b)
Saturday
c)
Sunday
d)
Monday

|
Ssc Cgl answered |
Total number of odd days from December 17, 1899 to December 22, 1901
14 + 356 + 356 = 735
or, 735/7 = 105
= 0 odd days
it was Saturday on December 17, 1899.
So, it will be Saturday on December 22, 1901.
14 + 356 + 356 = 735
or, 735/7 = 105
= 0 odd days
it was Saturday on December 17, 1899.
So, it will be Saturday on December 22, 1901.
How many times do the hands of a clock points towards each other in a day?- a)24
- b)20
- c)12
- d)22
Correct answer is option 'D'. Can you explain this answer?
How many times do the hands of a clock points towards each other in a day?
a)
24
b)
20
c)
12
d)
22
|
|
Arnav Saini answered |
Explanation:
Hands Pointing Towards Each Other:
- In a clock, the hour and minute hands point towards each other when they are at the same position.
- The minute hand completes a full rotation 12 times a day, while the hour hand completes two full rotations in the same period.
Calculation:
- When the clock strikes 12, both hands point towards each other.
- After this, the hands will point towards each other once every hour as the minute hand catches up with the hour hand.
- So, the hands point towards each other 11 more times in a day apart from the initial 12 o'clock position.
Total Times Hands Point Towards Each Other:
- The hands point towards each other a total of 12 times in a day.
Therefore, the correct answer is option 'D' - 22.
Hands Pointing Towards Each Other:
- In a clock, the hour and minute hands point towards each other when they are at the same position.
- The minute hand completes a full rotation 12 times a day, while the hour hand completes two full rotations in the same period.
Calculation:
- When the clock strikes 12, both hands point towards each other.
- After this, the hands will point towards each other once every hour as the minute hand catches up with the hour hand.
- So, the hands point towards each other 11 more times in a day apart from the initial 12 o'clock position.
Total Times Hands Point Towards Each Other:
- The hands point towards each other a total of 12 times in a day.
Therefore, the correct answer is option 'D' - 22.
If 2nd June 2013 is Sunday then which day was on 2nd June 2010?- a)Wednesday
- b)Friday
- c)Thursday
- d)Saturday
Correct answer is option 'A'. Can you explain this answer?
If 2nd June 2013 is Sunday then which day was on 2nd June 2010?
a)
Wednesday
b)
Friday
c)
Thursday
d)
Saturday

|
Ssc Cgl answered |
Consider from 2nd June 2010 to 2nd June 2013 we have total 2 non leap year and one leap year so number of odd days are 1 + 1 + 2 = 4 so 2nd June 2010 must be 4 days back from Sunday and that day is Wednesday.
From Zeller's Formula:
f = k + [13 x m - 1/ 5 ] + D + [D/4] + [C/4] - 2 x C.
In this case k = 2 (since 2nd June)
Month m = 4 (As march = 1, April = 2, May = 3, June = 4 )
D is the last two digit of year here D = 10 (As year is 2010)
C is 1 st two digit of century here C = 20 (As year is 2010)
f = 2 + [13 x 4 - 1 / 5] + 10 + [10/ 4] + [ 20/4] - 2 x 20.
f = 2 + [51/5] + 10 +[2.5] + [5] - 40.
f = 2 + 10 + 10 + 2 + 5 - 40 = -11
This - ve value of f can be made positive by adding multiple of 7
So f = - 11 + 14 = 3
When divided by 7 we will get remainder 3, hence number of odd days is 3,
So 2nd June 2010 is 3 days more than Monday, i.e Wednesday.
From Zeller's Formula:
f = k + [13 x m - 1/ 5 ] + D + [D/4] + [C/4] - 2 x C.
In this case k = 2 (since 2nd June)
Month m = 4 (As march = 1, April = 2, May = 3, June = 4 )
D is the last two digit of year here D = 10 (As year is 2010)
C is 1 st two digit of century here C = 20 (As year is 2010)
f = 2 + [13 x 4 - 1 / 5] + 10 + [10/ 4] + [ 20/4] - 2 x 20.
f = 2 + [51/5] + 10 +[2.5] + [5] - 40.
f = 2 + 10 + 10 + 2 + 5 - 40 = -11
This - ve value of f can be made positive by adding multiple of 7
So f = - 11 + 14 = 3
When divided by 7 we will get remainder 3, hence number of odd days is 3,
So 2nd June 2010 is 3 days more than Monday, i.e Wednesday.
A year 1991 is having a same calendar as that of the year X. Which of the following is a possible valueof X.
- a)2002
- b)2000
- c)1902
- d)1903
Correct answer is option 'A'. Can you explain this answer?
A year 1991 is having a same calendar as that of the year X. Which of the following is a possible valueof X.
a)
2002
b)
2000
c)
1902
d)
1903
|
|
Sameer Iyer answered |
Explanation:
A Leap Year in 1895:
- A leap year is a year that is evenly divisible by 4, except for years that are evenly divisible by 100 but not by 400.
- In 1895, the calendar followed the standard leap year rules, so it had 366 days.
Calendar Matching with Year X:
- To find a possible value of X that has the same calendar as 1895, we need to look for a year that is also a leap year.
- The leap years are generally every 4 years, so we need to find a year that is 4 years away from 1895.
Possible Value of X:
- The year that is 4 years after 1895 is 1899 (1895 + 4 = 1899).
- Since 1899 is a leap year (divisible by 4), it will have the same calendar as 1895.
- Therefore, a possible value of X is 1899.
Conclusion:
- Option 'a) 1901' is incorrect because it is not a leap year.
- Option 'b) 1900' is incorrect because it is not 4 years after 1895.
- Option 'c) 1902' is incorrect because it is not a leap year.
- Option 'd) 1903' is incorrect because it is not 4 years after 1895.
- The correct answer is option 'a) 1901' as it is 4 years after 1895 and a leap year.
A Leap Year in 1895:
- A leap year is a year that is evenly divisible by 4, except for years that are evenly divisible by 100 but not by 400.
- In 1895, the calendar followed the standard leap year rules, so it had 366 days.
Calendar Matching with Year X:
- To find a possible value of X that has the same calendar as 1895, we need to look for a year that is also a leap year.
- The leap years are generally every 4 years, so we need to find a year that is 4 years away from 1895.
Possible Value of X:
- The year that is 4 years after 1895 is 1899 (1895 + 4 = 1899).
- Since 1899 is a leap year (divisible by 4), it will have the same calendar as 1895.
- Therefore, a possible value of X is 1899.
Conclusion:
- Option 'a) 1901' is incorrect because it is not a leap year.
- Option 'b) 1900' is incorrect because it is not 4 years after 1895.
- Option 'c) 1902' is incorrect because it is not a leap year.
- Option 'd) 1903' is incorrect because it is not 4 years after 1895.
- The correct answer is option 'a) 1901' as it is 4 years after 1895 and a leap year.
Today is Sunday what day of the week was 79 days back.
- a)Tuesday
- b)Friday
- c)Thursday
- d)Saturday
Correct answer is option 'B'. Can you explain this answer?
Today is Sunday what day of the week was 79 days back.
a)
Tuesday
b)
Friday
c)
Thursday
d)
Saturday

|
Iq Funda answered |
When we divide 79 by 7 we will get remainder 2 so we have 2 odd days, so required day must be 2 days back from today (i.e Sunday) and that day should be Friday.
It was Sunday on Jan 1, 2006. What was the day of the Week Jan 1, 2010- a)Sunday
- b)Saturday
- c)Friday
- d)Wednesday
Correct answer is option 'C'. Can you explain this answer?
It was Sunday on Jan 1, 2006. What was the day of the Week Jan 1, 2010
a)
Sunday
b)
Saturday
c)
Friday
d)
Wednesday

|
Rithika Chavan answered |
On 31st December, 2005 it was Saturday.
Number of odd days from the year 2006 to the year 2009 = (1 + 1 + 2 + 1) = 5 days.
∴ On 31st December 2009, it was Thursday.
Thus, on 1st Jan, 2010 it is Friday.
Number of odd days from the year 2006 to the year 2009 = (1 + 1 + 2 + 1) = 5 days.
∴ On 31st December 2009, it was Thursday.
Thus, on 1st Jan, 2010 it is Friday.
If 28th August 1946 was a Wednesday, what day of the week was 31 August 1961?- a)Tuesday
- b)Monday
- c)Thursday
- d)Wednesday
Correct answer is option 'C'. Can you explain this answer?
If 28th August 1946 was a Wednesday, what day of the week was 31 August 1961?
a)
Tuesday
b)
Monday
c)
Thursday
d)
Wednesday

|
S.S Career Academy answered |
It is given that 28th August 1946 was Wednesday.
From 28th August 1946 to 28th August 1961, we have 4 leap years and 11 normal years.
So the number of odd days would be 11*1 + 4*2 = 19
Now the date which is asked is 31 Aug 1961. So if we move from 28th August to 31st August, we will have 3 more odd days.
So total number of odd days = 5 + 3 = 8
Now 8 mod 7 = 1 .
So 31st August 1961 would be Wednesday + 1 = Thursday.
Reaching the place of meeting on Tuesday 15 min before 8:30 h, Anuj found himself half an hour earlier than the man who was 40 min late. What was the scheduled time of the meeting ?- a)8:00 h
- b)8:05 h
- c)8:15 h
- d)8:45 h
Correct answer is option 'B'. Can you explain this answer?
Reaching the place of meeting on Tuesday 15 min before 8:30 h, Anuj found himself half an hour earlier than the man who was 40 min late. What was the scheduled time of the meeting ?
a)
8:00 h
b)
8:05 h
c)
8:15 h
d)
8:45 h

|
G.K Academy answered |
Anuj reached the place of meeting at 8:15 h, he reached 30 min earlier than the man who was 40 min late, Hence, the scheduled time of the meeting was 8:05 h.
A watch which gains uniformly is 2 minutes slow at noon on Sunday and is 4 min. 48 sec fast at 2 p.m. on the following Sunday. When it has shown the correct time ?- a)2 : 00 p.m. on Monday
- b)2 : 00 p.m. on Tuesday
- c)3 : 00 p.m. on Wednesday
- d)1 p.m. on Thrusday
Correct answer is option 'B'. Can you explain this answer?
A watch which gains uniformly is 2 minutes slow at noon on Sunday and is 4 min. 48 sec fast at 2 p.m. on the following Sunday. When it has shown the correct time ?
a)
2 : 00 p.m. on Monday
b)
2 : 00 p.m. on Tuesday
c)
3 : 00 p.m. on Wednesday
d)
1 p.m. on Thrusday

|
Iq Funda answered |
Time from 12 p.m. on Sunday to 2 p.m. on the following Sunday = 7 days 2 hours.
= 24 x 7 + 2 = 170 hours.
The watch gain = (2 + 4 x 4/5) min = 34/5 minute in 170 hrs.
Since, 34/5 min are gained in 170 hrs.
2 min are gained in (170 x 5/34 x 2) hrs = 50 hours i.e., 2 days 2 hrs.
after 12 p.m. on Sunday i.e., it will be correct at 2 p.m. on Tuesday.
= 24 x 7 + 2 = 170 hours.
The watch gain = (2 + 4 x 4/5) min = 34/5 minute in 170 hrs.
Since, 34/5 min are gained in 170 hrs.
2 min are gained in (170 x 5/34 x 2) hrs = 50 hours i.e., 2 days 2 hrs.
after 12 p.m. on Sunday i.e., it will be correct at 2 p.m. on Tuesday.
If in a particular year 'X' there are 53 Sundays then how many Sundays will be there in a period of four years X to X + 3 year.- a)208
- b)209
- c)208 or 209
- d)None of these
Correct answer is option 'B'. Can you explain this answer?
If in a particular year 'X' there are 53 Sundays then how many Sundays will be there in a period of four years X to X + 3 year.
a)
208
b)
209
c)
208 or 209
d)
None of these

|
G.K Academy answered |
Let us take two cases
Case (i) : When year start with Sunday then next 4 years will always have 52 Sundays hence total number of Sundays are 53 + 3 x 52 = 209 Sundays
Case (ii) : When year start with Sunday and then we have 53 Sundays that means year is a leap year then next 4 years will always have 52 Sundays hence total number of Sundays are 53 + 3 x 52 = 209 Sundays.
Case (i) : When year start with Sunday then next 4 years will always have 52 Sundays hence total number of Sundays are 53 + 3 x 52 = 209 Sundays
Case (ii) : When year start with Sunday and then we have 53 Sundays that means year is a leap year then next 4 years will always have 52 Sundays hence total number of Sundays are 53 + 3 x 52 = 209 Sundays.
How many times are the hands of a clock is at right angle in a day?- a)22
- b)24
- c)44
- d)48
Correct answer is option 'C'. Can you explain this answer?
How many times are the hands of a clock is at right angle in a day?
a)
22
b)
24
c)
44
d)
48
|
|
Pranab Goyal answered |
Explanation:
The minute hand of a clock makes 360 degrees in 60 minutes (1 hour), so it moves 6 degrees in 1 minute. The hour hand of a clock makes 360 degrees in 12 hours, so it moves 30 degrees in 1 hour.
At Right Angles:
- Two hands of a clock are at right angles when they are 90 degrees apart.
- This happens when the minute hand is at 3 and the hour hand is at 12, 6, or 9.
Calculating the Number of Times:
- The minute hand and hour hand will be at right angles 22 times in a day.
- The minute hand will be at 3 twelve times in a day (every 2 hours).
- Out of these twelve times, the hour hand will be at 12, 6, or 9 six times each.
- So, the total number of times the hands of a clock are at right angles in a day is 6 x 3 = 18.
- Additionally, the minute hand and hour hand are at right angles when the minute hand is at 9 and the hour hand is at 12.
- This happens four times in a day (every 3 hours).
- Therefore, the total number of times the hands of a clock are at right angles in a day = 18 + 4 = 22.
Therefore, the correct answer is option 'C', 44 times.
The minute hand of a clock makes 360 degrees in 60 minutes (1 hour), so it moves 6 degrees in 1 minute. The hour hand of a clock makes 360 degrees in 12 hours, so it moves 30 degrees in 1 hour.
At Right Angles:
- Two hands of a clock are at right angles when they are 90 degrees apart.
- This happens when the minute hand is at 3 and the hour hand is at 12, 6, or 9.
Calculating the Number of Times:
- The minute hand and hour hand will be at right angles 22 times in a day.
- The minute hand will be at 3 twelve times in a day (every 2 hours).
- Out of these twelve times, the hour hand will be at 12, 6, or 9 six times each.
- So, the total number of times the hands of a clock are at right angles in a day is 6 x 3 = 18.
- Additionally, the minute hand and hour hand are at right angles when the minute hand is at 9 and the hour hand is at 12.
- This happens four times in a day (every 3 hours).
- Therefore, the total number of times the hands of a clock are at right angles in a day = 18 + 4 = 22.
Therefore, the correct answer is option 'C', 44 times.
Today is Wednesday , what will be the day after 84 days?- a)Monday
- b)Tuesday
- c)Wednesday
- d)Sunday
Correct answer is option 'C'. Can you explain this answer?
Today is Wednesday , what will be the day after 84 days?
a)
Monday
b)
Tuesday
c)
Wednesday
d)
Sunday

|
Ssc Cgl answered |
Everyday of the weeks is repeated after 7 days.
Hence, it will be Wednesday after 84 days.
Hence, it will be Wednesday after 84 days.
The last day of a Century cannot be- a)Monday
- b)Wednesday
- c)Tuesday
- d)Friday
Correct answer is option 'C'. Can you explain this answer?
The last day of a Century cannot be
a)
Monday
b)
Wednesday
c)
Tuesday
d)
Friday

|
Malavika Rane answered |
100 years contain 5 odd days.
∴ Last day of 1st century is Friday.
200 years contain (5 x 2) ≡ 3 odd days.
∴ Last day of 2nd century is Wednesday.
300 years contain (5 x 3) = 15 ≡ 1 odd day.
∴ Last day of 3rd century is Monday.
400 years contain 0 odd day.
∴ Last day of 4th century is Sunday.
This cycle is repeated.
∴ Last day of a century cannot be Tuesday or Thursday or Saturday.
∴ Last day of 1st century is Friday.
200 years contain (5 x 2) ≡ 3 odd days.
∴ Last day of 2nd century is Wednesday.
300 years contain (5 x 3) = 15 ≡ 1 odd day.
∴ Last day of 3rd century is Monday.
400 years contain 0 odd day.
∴ Last day of 4th century is Sunday.
This cycle is repeated.
∴ Last day of a century cannot be Tuesday or Thursday or Saturday.
Which of the following two months in a particular year will have same calendar.- a)January and August
- b)January and October
- c)March and November
- d)None of these
Correct answer is option 'C'. Can you explain this answer?
Which of the following two months in a particular year will have same calendar.
a)
January and August
b)
January and October
c)
March and November
d)
None of these

|
Ssc Cgl answered |
January and August or October depends on leap year or non leap year. But if we find the number of odd days between March and November we will get number of odd days is 0 hence they will have same calendar.
In 2016, Mohan celebrated his birthday on Friday. Which will be the first year after 2016 when Mohan will celebrate his birthday on a Wednesday? (He was not born in January or February)- a)2020
- b)2023
- c)2021
- d)2025
Correct answer is option 'A'. Can you explain this answer?
In 2016, Mohan celebrated his birthday on Friday. Which will be the first year after 2016 when Mohan will celebrate his birthday on a Wednesday? (He was not born in January or February)
a)
2020
b)
2023
c)
2021
d)
2025

|
Innovative Classes answered |
Since it has been mentioned that Mohan was not born in February, so he can’t be born on 29th Feb.
Hence He will celebrate his next birthday on a Wednesday in the year for which the sum of the odd days becomes 5 or a multiple of 5.
By his birthday in 2017, there will be 1 odd day.
By his birthday in 2018, there will be 2 odd days.
By his birthday in 2019, there will be 3 odd days.
By his birthday in 2020, there will be 5 odd days, as 2020 is a leap year.
So in 2020 He will celebrate his birthday on Wednesday.
By how many degree does the minute hand move in the same time, in which the hour hand move by 28 ?- a)168
- b)336
- c)196
- d)376
Correct answer is option 'B'. Can you explain this answer?
By how many degree does the minute hand move in the same time, in which the hour hand move by 28 ?
a)
168
b)
336
c)
196
d)
376

|
Malavika Rane answered |
Calculation:
Hour hand moves 30 degrees in one hour.
Minute hand moves 360 degrees in one hour (60 minutes).
Difference in movement:
Hour hand moves 28 degrees, so the minute hand will move more than 28 degrees in the same time.
Calculation:
Minute hand moves 30 degrees in one hour more than the hour hand.
30 degrees * 12 hours (because there are 12 hours in a clock) = 360 degrees.
So, the minute hand moves 360 degrees more than the hour hand in 12 hours.
Answer:
Therefore, in the same time it takes for the hour hand to move by 28 degrees, the minute hand will move by 360 degrees, which is option B) 336.
Hour hand moves 30 degrees in one hour.
Minute hand moves 360 degrees in one hour (60 minutes).
Difference in movement:
Hour hand moves 28 degrees, so the minute hand will move more than 28 degrees in the same time.
Calculation:
Minute hand moves 30 degrees in one hour more than the hour hand.
30 degrees * 12 hours (because there are 12 hours in a clock) = 360 degrees.
So, the minute hand moves 360 degrees more than the hour hand in 12 hours.
Answer:
Therefore, in the same time it takes for the hour hand to move by 28 degrees, the minute hand will move by 360 degrees, which is option B) 336.
Find the angle between minute hand and hour hand at 10 : 10 AM- a)245°
- b)195°
- c)175°
- d)None of these
Correct answer is option 'A'. Can you explain this answer?
Find the angle between minute hand and hour hand at 10 : 10 AM
a)
245°
b)
195°
c)
175°
d)
None of these
|
|
Nilesh Banerjee answered |
Calculating the Angle between Minute Hand and Hour Hand at 10:10 AM
- At 10:10 AM, the minute hand is at 2 minutes past 10, and the hour hand is between 10 and 11.
- To calculate the angle between the minute hand and hour hand, we can use the formula:
Angle = |(30*H - (11/2)*M)|
where H is the hour and M is the minutes.
Calculating the Angle:
- H = 10
- M = 10
- Plugging the values into the formula:
Angle = |(30*10 - (11/2)*10)|
= |(300 - 55)|
= |245|
= 245°
Therefore, the angle between the minute hand and hour hand at 10:10 AM is 245°.
- At 10:10 AM, the minute hand is at 2 minutes past 10, and the hour hand is between 10 and 11.
- To calculate the angle between the minute hand and hour hand, we can use the formula:
Angle = |(30*H - (11/2)*M)|
where H is the hour and M is the minutes.
Calculating the Angle:
- H = 10
- M = 10
- Plugging the values into the formula:
Angle = |(30*10 - (11/2)*10)|
= |(300 - 55)|
= |245|
= 245°
Therefore, the angle between the minute hand and hour hand at 10:10 AM is 245°.
If today is Monday then which day of the week is after 59 days.- a)Tuesday
- b)Wednesday
- c)Thursday
- d)Friday
Correct answer is option 'C'. Can you explain this answer?
If today is Monday then which day of the week is after 59 days.
a)
Tuesday
b)
Wednesday
c)
Thursday
d)
Friday

|
EduRev SSC CGL answered |
Since a day of the week repeat after every 7 days, divide 59 by 7, remainder is 3 so number of odd days is 3, and 3 days after Monday is Thursday.
Which of the following day could be the 18th October 2050?- a)Tuesday
- b)Frfiday
- c)Thursday
- d)Saturday
Correct answer is option 'A'. Can you explain this answer?
Which of the following day could be the 18th October 2050?
a)
Tuesday
b)
Frfiday
c)
Thursday
d)
Saturday

|
Ssc Cgl answered |
From Zeller's Formula
f = k + [13 x m - 1 / 5] + D + [D/4] + [C/4] - 2 x C.
In this case k = 18 (since 18th October)
Month m = 8 (As march = 1, April = 2, May = 3, October = 8)
D is the last two digit of year here D = 50 (As year is 2050)
C is the 1st two digit of century here C = 20 (As year is 1950)
f = 18 + [13 x 8 - 1 / 5] + 50 + [50/4] + [20/4] - 2 x 20.
f = 18 + [103/5] + 50 + [12.5] + [5] - 40.
f = 18 + 20 + 50 + 12 + 5 - 40 = 65.
When divided by 7 we will get remainder 2, hence number of odd days is 2,
So 18th October 2050 is 2 days more than Sunday, i.e Tuesday.
f = k + [13 x m - 1 / 5] + D + [D/4] + [C/4] - 2 x C.
In this case k = 18 (since 18th October)
Month m = 8 (As march = 1, April = 2, May = 3, October = 8)
D is the last two digit of year here D = 50 (As year is 2050)
C is the 1st two digit of century here C = 20 (As year is 1950)
f = 18 + [13 x 8 - 1 / 5] + 50 + [50/4] + [20/4] - 2 x 20.
f = 18 + [103/5] + 50 + [12.5] + [5] - 40.
f = 18 + 20 + 50 + 12 + 5 - 40 = 65.
When divided by 7 we will get remainder 2, hence number of odd days is 2,
So 18th October 2050 is 2 days more than Sunday, i.e Tuesday.
Chapter doubts & questions for Clock & Calender - General Intelligence and Reasoning for SSC CGL 2025 is part of SSC CGL exam preparation. The chapters have been prepared according to the SSC CGL exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for SSC CGL 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of Clock & Calender - General Intelligence and Reasoning for SSC CGL in English & Hindi are available as part of SSC CGL exam.
Download more important topics, notes, lectures and mock test series for SSC CGL Exam by signing up for free.
General Intelligence and Reasoning for SSC CGL
201 videos|226 docs|197 tests
|

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily









