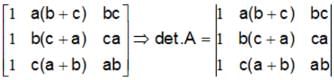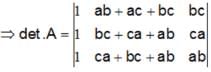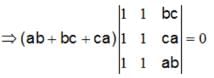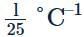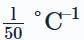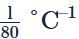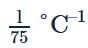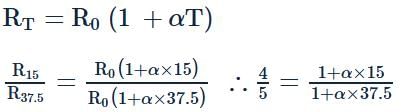All Exams >
JEE >
Weekly Tests for JEE Preparation >
All Questions
All questions of June Week 2 for JEE Exam
In a meter bridge experiment a balance point is obtained at a distance of 60 cm from the left end when unknown resistance R is in a left gap and 8 ohms resistor is connected in the right gap. When the position of R and 8 ohm resistor is interchanged the balance point will be at distance of- a)40 cm
- b)30 cm
- c)50 cm
- d)60 cm
Correct answer is option 'A'. Can you explain this answer?
In a meter bridge experiment a balance point is obtained at a distance of 60 cm from the left end when unknown resistance R is in a left gap and 8 ohms resistor is connected in the right gap. When the position of R and 8 ohm resistor is interchanged the balance point will be at distance of
a)
40 cm
b)
30 cm
c)
50 cm
d)
60 cm
|
|
Jyoti Sengupta answered |
60/40 = l/100-l, = R/8
so R=12
now changed position 8 is proportional to l and 12 to (100-l)
8/12 = l/100-l
l = 40ohm
Can you explain the answer of this question below:If A and B are invertible matrices of order 3 , then det (adj A) =
- A:
(detA)2
- B:
1
- C:
A−1
- D:
none of these
The answer is d.
If A and B are invertible matrices of order 3 , then det (adj A) =
(detA)2
1
A−1
none of these

|
Sinjini Tiwari answered |
Let A be a non singular square matrix of order n . then , |adj.A| = A−1
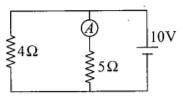
Meter Bridge is used to- a)determine unknown voltage v
- b)determine unknown resistance R
- c)determine unknown power P
- d)determine unknown emf e
Correct answer is option 'B'. Can you explain this answer?
Meter Bridge is used to
a)
determine unknown voltage v
b)
determine unknown resistance R
c)
determine unknown power P
d)
determine unknown emf e

|
Maulik Mehra answered |
Explanation:With a known resistance in one of the gaps, the meter bridge is used to determine the value of unknown resistance by the formula.

- a)−2(a+b+c)3
- b)2(a+b+c)2
- c)4(a+b+c)3
- d)none of these
Correct answer is option 'D'. Can you explain this answer?
a)
−2(a+b+c
)3
b)
2(a+b+c)2
c)
4(a+b+c)3
d)
none of these

|
Sushil Kumar answered |
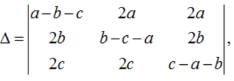
Apply , R1 → R1+R2+R3,

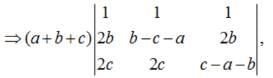
Apply , C3→ C3 - C1, C2→C2 - C1,
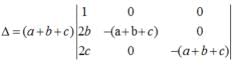
=(a+b+c)3
The Wheatstone bridge is balanced for four resistors R1,R2,R3 and R4 with a cell of emf 1.46 V. The cell is now replaced by another cell of emf 1.08 V. To obtain the balance again
- a)All the four resistance should be changed
- b)Both the resistance R1 and R4 should be changed
- c)No resistance needs to be changed
- d)Resistance R4 should be changed only
Correct answer is option 'C'. Can you explain this answer?
The Wheatstone bridge is balanced for four resistors R1,R2,R3 and R4 with a cell of emf 1.46 V. The cell is now replaced by another cell of emf 1.08 V. To obtain the balance again
a)
All the four resistance should be changed
b)
Both the resistance R1 and R4 should be changed
c)
No resistance needs to be changed
d)
Resistance R4 should be changed only
|
|
Neha Sharma answered |
The balance point of the Wheatstone’s bridge is determined by the ratio of the resistances. The change in the emf of the external battery will have no effect on the balance point.
Explanation:
- Initial Balanced Wheatstone Bridge: In the initial balanced Wheatstone bridge configuration, the emf of the cell is 1.46 V and all four resistors R1, R2, R3, and R4 are set to specific values to achieve balance.
- Replacement of Cell: When the cell is replaced by another cell with an emf of 1.08 V, the balance of the Wheatstone bridge is disrupted.
- Requirement for Rebalancing: In order to rebalance the Wheatstone bridge with the new cell of emf 1.08 V, no resistance needs to be changed.
- Reasoning: The balance of the Wheatstone bridge is determined by the ratio of the resistances in the bridge arms and not by the absolute values of the resistances. As long as the ratio of the resistances remains the same, the balance will be maintained regardless of the emf of the cell.
- Conclusion: Therefore, in this scenario, no resistance needs to be changed to obtain the balance again with the new cell of emf 1.08 V.
A voltmeter has a resistance of G ohm and range V volt. The value of resistance used in series to convert it into voltmeter of range nV volt is- a)nG
- b)(n−1)G
- c)G/n
- d)G/(n−1)
Correct answer is option 'B'. Can you explain this answer?
A voltmeter has a resistance of G ohm and range V volt. The value of resistance used in series to convert it into voltmeter of range nV volt is
a)
nG
b)
(n−1)G
c)
G/n
d)
G/(n−1)
|
|
Avantika Mehta answered |
Understanding Voltmeter Conversion
To convert a voltmeter of range V volts into a voltmeter of range nV volts, we need to consider the resistance of the voltmeter and the additional resistance required in series.
Principle of Operation
- A voltmeter measures the potential difference across its terminals.
- When converting to a higher range, we add a series resistance to ensure that the voltmeter can handle the increased voltage without damaging its internal components.
Given Parameters
- Resistance of the voltmeter = G ohm
- Original range of the voltmeter = V volts
- New desired range = nV volts
Calculating Series Resistance
1. Voltage Division: When a voltmeter with resistance G is connected in series with another resistance R, the voltage drop across the voltmeter is a fraction of the total voltage.
2. Using Voltage Ratios: The voltage across the voltmeter can be given by the ratio:
- V / (V + R) = G / (G + R)
3. Setting Up the Equation: For the new range of nV:
- nV / (nV + R) = G / (G + R)
4. Solving for R: Rearranging gives us:
- R = (n-1)G
This means the resistance required in series to achieve the desired range of nV volts is (n - 1)G ohms.
Conclusion
Thus, the correct answer for the resistance used in series to convert the voltmeter into one of range nV volts is option B: (n - 1)G. This ensures proper functioning and safety of the voltmeter under higher voltage conditions.
To convert a voltmeter of range V volts into a voltmeter of range nV volts, we need to consider the resistance of the voltmeter and the additional resistance required in series.
Principle of Operation
- A voltmeter measures the potential difference across its terminals.
- When converting to a higher range, we add a series resistance to ensure that the voltmeter can handle the increased voltage without damaging its internal components.
Given Parameters
- Resistance of the voltmeter = G ohm
- Original range of the voltmeter = V volts
- New desired range = nV volts
Calculating Series Resistance
1. Voltage Division: When a voltmeter with resistance G is connected in series with another resistance R, the voltage drop across the voltmeter is a fraction of the total voltage.
2. Using Voltage Ratios: The voltage across the voltmeter can be given by the ratio:
- V / (V + R) = G / (G + R)
3. Setting Up the Equation: For the new range of nV:
- nV / (nV + R) = G / (G + R)
4. Solving for R: Rearranging gives us:
- R = (n-1)G
This means the resistance required in series to achieve the desired range of nV volts is (n - 1)G ohms.
Conclusion
Thus, the correct answer for the resistance used in series to convert the voltmeter into one of range nV volts is option B: (n - 1)G. This ensures proper functioning and safety of the voltmeter under higher voltage conditions.
A piece of copper and another of germanium are cooled from room temperature to 80K. The resistance- a)of each of them decreases
- b)of each of them increases
- c)copper increases and that of germanium decreases
- d)copper decreases and that of germanium increases
Correct answer is option 'D'. Can you explain this answer?
A piece of copper and another of germanium are cooled from room temperature to 80K. The resistance
a)
of each of them decreases
b)
of each of them increases
c)
copper increases and that of germanium decreases
d)
copper decreases and that of germanium increases

|
Pranjal Pillai answered |
Explanation:Copper is a conductor and we know that for conductors, resistance is directly proprtional to temperature. Therefore on decreasing temperature resistance also decreases.Whereas, germanium is a semiconductor and for semiconductors, resistance is inversely proportional to temperature. So on decreasing temperature resistance increases.
If the system of equations
2x + 3y - z = 5
x + αy + 3z = -4
3x - y + βz = 7
has infinitely many solutions, then 13αβ is equal to- a)1110
- b)1120
- c)1210
- d)1220
Correct answer is option 'B'. Can you explain this answer?
If the system of equations
2x + 3y - z = 5
x + αy + 3z = -4
3x - y + βz = 7
has infinitely many solutions, then 13αβ is equal to
2x + 3y - z = 5
x + αy + 3z = -4
3x - y + βz = 7
has infinitely many solutions, then 13αβ is equal to
a)
1110
b)
1120
c)
1210
d)
1220

|
Manish Aggarwal answered |
Using family of planes
2x + 3y - z - 5 = k₁(x + αy + 3z + 4) + k₂(3x - y + βz - 7)
2 = k₁ + 3k₂, 3 = k₁α - k₂, -1 = 3k₁ + βk₂, -5 = 4k₁ - 7k₂
On solving we get
k₂ = 13/19, k₁ = -1/19, α = -70, β = -16/13
13αβ = 13(-70)(-16/13) = 1120
2x + 3y - z - 5 = k₁(x + αy + 3z + 4) + k₂(3x - y + βz - 7)
2 = k₁ + 3k₂, 3 = k₁α - k₂, -1 = 3k₁ + βk₂, -5 = 4k₁ - 7k₂
On solving we get
k₂ = 13/19, k₁ = -1/19, α = -70, β = -16/13
13αβ = 13(-70)(-16/13) = 1120
In a metre bridge experiment, null point is obtained at 20 cm from one end of the wire when resistance X is balanced against another resistance Y. If X<Y, then where will be the new position of the null point from the same end, if one decides to balance a resistance of 4X against Y ?- a)50 cm
- b)80 cm
- c)40 cm
- d)70 cm
Correct answer is option 'A'. Can you explain this answer?
In a metre bridge experiment, null point is obtained at 20 cm from one end of the wire when resistance X is balanced against another resistance Y. If X<Y, then where will be the new position of the null point from the same end, if one decides to balance a resistance of 4X against Y ?
a)
50 cm
b)
80 cm
c)
40 cm
d)
70 cm
|
|
Pranab Kapoor answered |
Understanding the Metre Bridge Experiment
In a metre bridge experiment, the balance point (null point) indicates the equality of the ratios of resistances. Here’s a detailed explanation of how to determine the new null point when balancing different resistances.
Initial Setup
- A null point is found at 20 cm from one end of the wire when resistance X is balanced against resistance Y.
- This can be expressed as:
(X / Y) = (Length from one end / Length from the other end)
Thus, (X / Y) = (20 cm / 80 cm) = 1/4.
- Given that X < y,="" we="" can="" infer="" that="" x="" />
New Resistance Balancing
- Now, we are tasked with balancing a resistance of 4X against Y.
- The new equation becomes (4X / Y) = (Length from one end / Length from the other end).
Calculating New Null Point
- From the previous relationship, we know that X = (1/4)Y, therefore:
4X = 4 * (1/4)Y = Y.
- This implies that when balancing 4X against Y, they are equal.
- Hence, the new null point would be halfway along the bridge length, which is at 50 cm from one end.
Conclusion
- Therefore, when balancing a resistance of 4X against Y, the new null point will be at 50 cm from the original end.
- Thus, the correct answer is option a) 50 cm.
In a metre bridge experiment, the balance point (null point) indicates the equality of the ratios of resistances. Here’s a detailed explanation of how to determine the new null point when balancing different resistances.
Initial Setup
- A null point is found at 20 cm from one end of the wire when resistance X is balanced against resistance Y.
- This can be expressed as:
(X / Y) = (Length from one end / Length from the other end)
Thus, (X / Y) = (20 cm / 80 cm) = 1/4.
- Given that X < y,="" we="" can="" infer="" that="" x="" />
New Resistance Balancing
- Now, we are tasked with balancing a resistance of 4X against Y.
- The new equation becomes (4X / Y) = (Length from one end / Length from the other end).
Calculating New Null Point
- From the previous relationship, we know that X = (1/4)Y, therefore:
4X = 4 * (1/4)Y = Y.
- This implies that when balancing 4X against Y, they are equal.
- Hence, the new null point would be halfway along the bridge length, which is at 50 cm from one end.
Conclusion
- Therefore, when balancing a resistance of 4X against Y, the new null point will be at 50 cm from the original end.
- Thus, the correct answer is option a) 50 cm.
If I3 is the identity matrix of order 3 , then 13−1 is- a)0
- b)3I3
- c)I3
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If I3 is the identity matrix of order 3 , then 13−1 is
a)
0
b)
3I3
c)
I3
d)
none of these

|
Pranavi Iyer answered |
Because , the inverse of an identity matrix is an identity matrix.
In a third order determinant, each element of the first column consists of sum of two terms, each element of the second column consists of sum of three terms and each element of the third column consists of sum of four terms. Then it can be decomposed into n determinants, where n has value- a)1
- b)9
- c)24
- d)16
Correct answer is option 'C'. Can you explain this answer?
In a third order determinant, each element of the first column consists of sum of two terms, each element of the second column consists of sum of three terms and each element of the third column consists of sum of four terms. Then it can be decomposed into n determinants, where n has value
a)
1
b)
9
c)
24
d)
16

|
Ipsita Sen answered |
N = 2 ×3 × 4 = 24.
If A’ is the transpose of a square matrix A , then- a)|A| ≠ |A′|
- b)|A|+|A′| = 0
- c)|A| = |A′|
- d)none of these
Correct answer is option 'C'. Can you explain this answer?
If A’ is the transpose of a square matrix A , then
a)
|A| ≠ |A′|
b)
|A|+|A′| = 0
c)
|A| = |A′|
d)
none of these

|
Ipsita Sen answered |
The determinant of a matrix A and its transpose always same.
According to Kirchhoff’s Loop Rule
- a)The absolute sum of changes in potential around any closed loop must be same.
- b)The algebraic sum of changes in potential around any closed loop must be negative.
- c)The algebraic sum of changes in potential around any closed loop must be positive.
- d)The algebraic sum of changes in potential around any closed loop must be zero.
Correct answer is option 'D'. Can you explain this answer?
According to Kirchhoff’s Loop Rule
a)
The absolute sum of changes in potential around any closed loop must be same.
b)
The algebraic sum of changes in potential around any closed loop must be negative.
c)
The algebraic sum of changes in potential around any closed loop must be positive.
d)
The algebraic sum of changes in potential around any closed loop must be zero.
|
|
Neha Chauhan answered |
Kirchhoff’s loop rule is based on the principle of conservation of energy. The work done in transporting a charge in a closed loop is zero. The algebraic sum ( since potential differences can be both positive and negative) of potential differences around any closed loop is always zero.
Consider the system of linear equations
x + y + z = 5,
x + 2y + λ²z = 9,
x + 3y + λz = μ, where λ, μ ∈ R.
Then, which of the following statement is NOT correct?- a)System has infinite number of solutions if λ = 1 and μ = 13
- b)System is inconsistent if λ = 1 and μ ≠ 13
- c)System is consistent if λ ≠ 1 and μ = 13
- d)System has unique solution if λ ≠ 1 and μ ≠ 13
Correct answer is option 'D'. Can you explain this answer?
Consider the system of linear equations
x + y + z = 5,
x + 2y + λ²z = 9,
x + 3y + λz = μ, where λ, μ ∈ R.
Then, which of the following statement is NOT correct?
x + y + z = 5,
x + 2y + λ²z = 9,
x + 3y + λz = μ, where λ, μ ∈ R.
Then, which of the following statement is NOT correct?
a)
System has infinite number of solutions if λ = 1 and μ = 13
b)
System is inconsistent if λ = 1 and μ ≠ 13
c)
System is consistent if λ ≠ 1 and μ = 13
d)
System has unique solution if λ ≠ 1 and μ ≠ 13
|
|
Navya Chakraborty answered |
Understanding the System of Equations
The given system of equations is:
1. x + y + z = 5
2. x + 2y + λ²z = 9
3. x + 3y + λz = μ
Here, λ and μ are real numbers that influence the solution of the system.
Analyzing the Conditions
1. Infinite Solutions (λ = 1, μ = 13):
- If λ = 1, the second equation becomes x + 2y + z = 9.
- The third equation becomes x + 3y + z = 13.
- The first equation leads to a contradiction with the others, thus the system has infinite solutions.
2. Inconsistent System (λ = 1, μ ≠ 13):
- If μ is not equal to 13, the third equation will not align with the first two, causing inconsistency.
3. Consistent System (λ ≠ 1, μ = 13):
- When λ is not equal to 1, the equations can still yield a solution, particularly aligning with μ = 13.
4. Unique Solution (λ ≠ 1, μ ≠ 13):
- This scenario claims that a unique solution exists. However, this is incorrect because the system may still be dependent, leading to infinite solutions or inconsistency depending on the values of λ and μ.
Conclusion
The statement that the system has a unique solution if λ ≠ 1 and μ ≠ 13 is NOT correct. The system can either be consistent with infinite solutions or inconsistent based on the choices of λ and μ. Thus, option 'D' is the correct answer.
The given system of equations is:
1. x + y + z = 5
2. x + 2y + λ²z = 9
3. x + 3y + λz = μ
Here, λ and μ are real numbers that influence the solution of the system.
Analyzing the Conditions
1. Infinite Solutions (λ = 1, μ = 13):
- If λ = 1, the second equation becomes x + 2y + z = 9.
- The third equation becomes x + 3y + z = 13.
- The first equation leads to a contradiction with the others, thus the system has infinite solutions.
2. Inconsistent System (λ = 1, μ ≠ 13):
- If μ is not equal to 13, the third equation will not align with the first two, causing inconsistency.
3. Consistent System (λ ≠ 1, μ = 13):
- When λ is not equal to 1, the equations can still yield a solution, particularly aligning with μ = 13.
4. Unique Solution (λ ≠ 1, μ ≠ 13):
- This scenario claims that a unique solution exists. However, this is incorrect because the system may still be dependent, leading to infinite solutions or inconsistency depending on the values of λ and μ.
Conclusion
The statement that the system has a unique solution if λ ≠ 1 and μ ≠ 13 is NOT correct. The system can either be consistent with infinite solutions or inconsistent based on the choices of λ and μ. Thus, option 'D' is the correct answer.
The resistance of a galvanometer is 10Ω. It gives full-scale deflection when 1 mA current is passed. The resistance connected in series for converting it into a voltmeter of 2.5 V will be- a)24.9Ω
- b)249Ω
- c)2490Ω
- d)24900Ω
Correct answer is option 'C'. Can you explain this answer?
The resistance of a galvanometer is 10Ω. It gives full-scale deflection when 1 mA current is passed. The resistance connected in series for converting it into a voltmeter of 2.5 V will be
a)
24.9Ω
b)
249Ω
c)
2490Ω
d)
24900Ω
|
|
Avantika Mehta answered |
Understanding the Galvanometer
A galvanometer is an instrument that detects and measures small electric currents. In this case, the galvanometer has a resistance of 10 Ω and shows full-scale deflection with a current of 1 mA.
Calculating Maximum Voltage
To convert the galvanometer into a voltmeter, we need to calculate the maximum voltage it can measure. This is done using Ohm's law (V = I × R):
- Maximum Voltage (Vg) = Current (I) × Resistance (Rg)
- Vg = 1 mA × 10 Ω = 0.001 A × 10 Ω = 0.01 V or 10 mV
Required Voltage for Voltmeter
The goal is to convert it into a voltmeter that can measure up to 2.5 V.
Series Resistance Calculation
To achieve this, we must add a series resistor (Rs) to the galvanometer. The total voltage (V) across the combination of the galvanometer and the resistor should equal 2.5 V:
- Total Voltage (V) = Vg + Voltage across Rs
- 2.5 V = 0.01 V + (I × Rs)
Since I is 1 mA (0.001 A), we rearrange to find Rs:
- 2.5 V = 0.01 V + (0.001 A × Rs)
- Rs = (2.5 V - 0.01 V) / 0.001 A
- Rs = (2.49 V) / (0.001 A) = 2490 Ω
Conclusion
The resistance that needs to be connected in series to convert the galvanometer into a voltmeter capable of measuring 2.5 V is 2490 Ω. Thus, the correct answer is option 'C'.
A galvanometer is an instrument that detects and measures small electric currents. In this case, the galvanometer has a resistance of 10 Ω and shows full-scale deflection with a current of 1 mA.
Calculating Maximum Voltage
To convert the galvanometer into a voltmeter, we need to calculate the maximum voltage it can measure. This is done using Ohm's law (V = I × R):
- Maximum Voltage (Vg) = Current (I) × Resistance (Rg)
- Vg = 1 mA × 10 Ω = 0.001 A × 10 Ω = 0.01 V or 10 mV
Required Voltage for Voltmeter
The goal is to convert it into a voltmeter that can measure up to 2.5 V.
Series Resistance Calculation
To achieve this, we must add a series resistor (Rs) to the galvanometer. The total voltage (V) across the combination of the galvanometer and the resistor should equal 2.5 V:
- Total Voltage (V) = Vg + Voltage across Rs
- 2.5 V = 0.01 V + (I × Rs)
Since I is 1 mA (0.001 A), we rearrange to find Rs:
- 2.5 V = 0.01 V + (0.001 A × Rs)
- Rs = (2.5 V - 0.01 V) / 0.001 A
- Rs = (2.49 V) / (0.001 A) = 2490 Ω
Conclusion
The resistance that needs to be connected in series to convert the galvanometer into a voltmeter capable of measuring 2.5 V is 2490 Ω. Thus, the correct answer is option 'C'.
Potentiometer measures the potential difference more accurately than a voltmeter, because- a)It draws a heavy current from external circuit.
- b)It does not draw current from external circuit.
- c)it has a wire of low resistance.
- d)it has a wire of high resistance
Correct answer is option 'B'. Can you explain this answer?
Potentiometer measures the potential difference more accurately than a voltmeter, because
a)
It draws a heavy current from external circuit.
b)
It does not draw current from external circuit.
c)
it has a wire of low resistance.
d)
it has a wire of high resistance

|
Amar Pillai answered |
Explanation:Potentiometer measures the potential difference using null deflection method, where no current is drawn from the cell; whereas voltmeter needs a small current to show deflection. So, accurate measurement of p.d is done using a potentiometer.
Drift is the random motion of the charged particles within a conductor,- a)along with a very slow net motion in the opposite direction of the field
- b)along with zero motion in the direction of the field
- c)along with a decelerated motion in the direction of the field
- d)along with accelerated motion in the direction of the field
Correct answer is option 'A'. Can you explain this answer?
Drift is the random motion of the charged particles within a conductor,
a)
along with a very slow net motion in the opposite direction of the field
b)
along with zero motion in the direction of the field
c)
along with a decelerated motion in the direction of the field
d)
along with accelerated motion in the direction of the field

|
Pranjal Pillai answered |
Explanation:The electrons in a conductor have random velocities and when an electric field is applied, they suffer repeated collisions and in the process move with a small average velocity, opposite to the direction of the field. This is equivalent to positive charge flowing in the direction of the field.
If A is a non singular matrix of order 3 , then |adj(A3)| =- a)|A|9
- b)|A|6
- c)|A|8
- d)none of these
Correct answer is 'B'. Can you explain this answer?
If A is a non singular matrix of order 3 , then |adj(A3)| =
a)
|A|9
b)
|A|6
c)
|A|8
d)
none of these

|
Aniket Basu answered |
If A is anon singular matrix of order , then 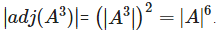
In a potentiometer experiment, for measuring internal resistance of a cell, the balance point has been obtained on the fourth wire. The balance point can be shifted to fifth wire by- a)increasing the current due to auxiliary battery
- b)Putting a shunt resistance in parallel with the cell.
- c)decreasing the current due to auxiliary battery
- d)putting a suitable resistance in series with the cell.
Correct answer is option 'C'. Can you explain this answer?
In a potentiometer experiment, for measuring internal resistance of a cell, the balance point has been obtained on the fourth wire. The balance point can be shifted to fifth wire by
a)
increasing the current due to auxiliary battery
b)
Putting a shunt resistance in parallel with the cell.
c)
decreasing the current due to auxiliary battery
d)
putting a suitable resistance in series with the cell.

|
Pranjal Pillai answered |
Explanation:If the current due to the auxillary battery is decreased, the potential gradient will be decreases, so the balancing length increases.Thus null point will move to fifth wire.
The sensitivity of the potentiometer can be increased by:- a)increasing the length of potentiometer wire.
- b)increasing the e.m.f. of primary cell.
- c)decreasing the length of potentiometer wire.
- d)increasing the potential gradient.
Correct answer is option 'A'. Can you explain this answer?
The sensitivity of the potentiometer can be increased by:
a)
increasing the length of potentiometer wire.
b)
increasing the e.m.f. of primary cell.
c)
decreasing the length of potentiometer wire.
d)
increasing the potential gradient.

|
Anjali Reddy answered |
Explanation:A potentiometer is considered to be sensitive if the potential gradient dV/dl is low. Such a potentiometer can measure very small changes in potential difference. Increasing the length of the potentiometer wire decreases the potential gradient. Its sensitivity increases. Increasing potential gradient decreases the sensitivity. increasing the emf of the primary cell and by decreasing the length, potential gradient increases.
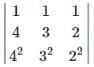 is equal to
is equal to - a)2
- b)1
- c)-2
- d)0
Correct answer is option 'C'. Can you explain this answer?
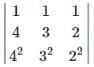 is equal to
is equal to a)
2
b)
1
c)
-2
d)
0

|
Ipsita Sen answered |
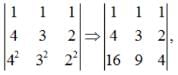
Apply , C1→C1 - C3, C2→C2-C3

= 10 - 12 = -2
In the figure, voltmeter and ammeter shown are ideal. Then voltmeter and ammeter readings, respectively, are
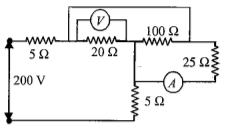
- a)125 V,3 A
- b)100 V,4 A
- c)120 V,4 A
- d)120 V,3 A
Correct answer is option 'B'. Can you explain this answer?
In the figure, voltmeter and ammeter shown are ideal. Then voltmeter and ammeter readings, respectively, are


a)
125 V,3 A
b)
100 V,4 A
c)
120 V,4 A
d)
120 V,3 A

|
Ambition Institute answered |
Resistors 20Ω,100Ω and 25Ω will be in parallel. Their equivalent is 10Ω.
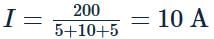
p.d. across 10Ω,10I = 10 × 10 = 100 V
This will be the voltmeter reading. Also, this will be the p.d. across each of 20Ω,100Ω and 25Ω resistors.
Ammeter reading = current through 25Ω=100/25=4 A.

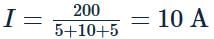
p.d. across 10Ω,10I = 10 × 10 = 100 V
This will be the voltmeter reading. Also, this will be the p.d. across each of 20Ω,100Ω and 25Ω resistors.
Ammeter reading = current through 25Ω=100/25=4 A.
The roots of the equation det. 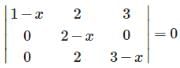 are
are- a)1 , 2, and 3
- b)1 and 3
- c)2, and 3
- d)none of these.
Correct answer is option 'A'. Can you explain this answer?
The roots of the equation det. 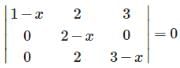 are
are
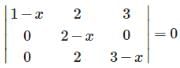 are
area)
1 , 2, and 3
b)
1 and 3
c)
2, and 3
d)
none of these.

|
Ujwal Chawla answered |

⇒ (1-x)(2-x)(3-x) = 0 ⇒x = 1,2,3
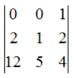
Let A = 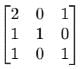 B = [ B₁, B₂, B₃ ], where B₁, B₂, B₃ are column matrices, and
B = [ B₁, B₂, B₃ ], where B₁, B₂, B₃ are column matrices, and 
If α = |B| and β is the sum of all the diagonal elements of B, then α³ + β³ is equal toCorrect answer is '28'. Can you explain this answer?
Let A = 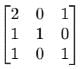 B = [ B₁, B₂, B₃ ], where B₁, B₂, B₃ are column matrices, and
B = [ B₁, B₂, B₃ ], where B₁, B₂, B₃ are column matrices, and 
If α = |B| and β is the sum of all the diagonal elements of B, then α³ + β³ is equal to
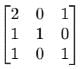 B = [ B₁, B₂, B₃ ], where B₁, B₂, B₃ are column matrices, and
B = [ B₁, B₂, B₃ ], where B₁, B₂, B₃ are column matrices, and 
If α = |B| and β is the sum of all the diagonal elements of B, then α³ + β³ is equal to

|
EduRev JEE answered |
x₁ = 1, y₁ = -1, z₁ = -1
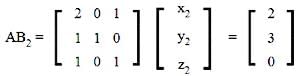
x₂ = 2, y₂ = 1, z₂ = -2
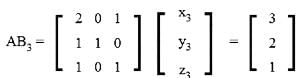
x₃ = 2, y₃ = 0, z₃ = -1
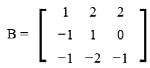
α = |B| = 3
β = 1
α³ + β³ = 27 + 1 = 28
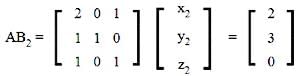
x₂ = 2, y₂ = 1, z₂ = -2
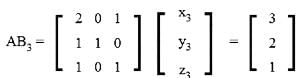
x₃ = 2, y₃ = 0, z₃ = -1
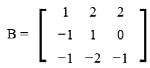
α = |B| = 3
β = 1
α³ + β³ = 27 + 1 = 28
If f(x) = 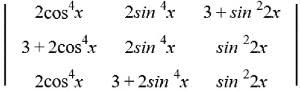 then (1/5) f'(0) is equal to
then (1/5) f'(0) is equal to- a)1
- b)0
- c)2
- d)6
Correct answer is option 'B'. Can you explain this answer?
If f(x) = 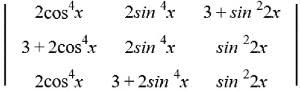 then (1/5) f'(0) is equal to
then (1/5) f'(0) is equal to
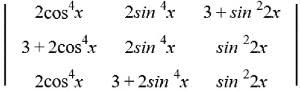 then (1/5) f'(0) is equal to
then (1/5) f'(0) is equal toa)
1
b)
0
c)
2
d)
6

|
Learners Habitat answered |
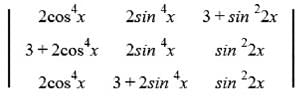
R₂ → R₂ - R₁, R₃ → R₃ - R₁
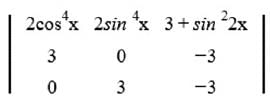
On applying determinant formula, we get
2cos⁴x * (0-(-9)) - 2sin⁴x * (-9-0) + (3 + sin²2x) * (9-0)
2cos⁴x * 9 - 2sin⁴x * (-9) + (3 + sin²2x) * 9
18cos⁴x +18 sin⁴x + (3 + sin²2x) * 9
18cos⁴x + 18sin⁴x + 27 + 9sin²2x
We are to find:
(1/5)·f'(0)
Step 1: Differentiate f(x)
We differentiate each term with respect to x:
Term 1: 18cos⁴x
Use the chain rule:
d/dx [cos⁴x] = 4cos³x * (−sinx) = −4cos³x sinx
So:
d/dx [18cos⁴x] = 18 × (−4cos³x sinx) = −72cos³x sinx
d/dx [cos⁴x] = 4cos³x * (−sinx) = −4cos³x sinx
So:
d/dx [18cos⁴x] = 18 × (−4cos³x sinx) = −72cos³x sinx
Term 2: 18sin⁴x
d/dx [sin⁴x] = 4sin³x * cosx
So:
d/dx [18sin⁴x] = 18 × 4sin³x cosx = 72sin³x cosx
So:
d/dx [18sin⁴x] = 18 × 4sin³x cosx = 72sin³x cosx
Term 3: 27 → derivative is 0
Term 4: 9sin²(2x)
Use chain rule:
d/dx [sin²(2x)] = 2sin(2x) * cos(2x) * 2 = 4sin(2x)cos(2x)
So:
d/dx [9sin²(2x)] = 9 × 4sin(2x)cos(2x) = 36sin(2x)cos(2x)
d/dx [sin²(2x)] = 2sin(2x) * cos(2x) * 2 = 4sin(2x)cos(2x)
So:
d/dx [9sin²(2x)] = 9 × 4sin(2x)cos(2x) = 36sin(2x)cos(2x)
Step 2: Combine derivatives
So,
f′(x) = −72cos³x sinx + 72sin³x cosx + 36sin(2x)cos(2x)
Step 3: Evaluate f′(0)
Plug in x = 0:
- sin(0) = 0
- cos(0) = 1
- sin(2×0) = 0
- cos(2×0) = 1
Now evaluate each term:
- −72cos³(0) sin(0) = −72(1)(0) = 0
- 72sin³(0) cos(0) = 72(0)(1) = 0
- 36sin(0)cos(0) = 36(0)(1) = 0
So,
f′(0) = 0
Step 4: Final Answer
(1/5) × f′(0) = (1/5) × 0 = 0
A square matrix A is invertible iff det A is equal to- a)0
- b)–1
- c)1
- d)non zero
Correct answer is option 'D'. Can you explain this answer?
A square matrix A is invertible iff det A is equal to
a)
0
b)
–1
c)
1
d)
non zero

|
Sarthak Verma answered |
Only non-singular matrices possess inverse.
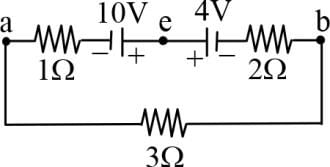
Three identical cells, each having an e.m.f. of 1.5 V and a constant internal resistance of 2.0Ω, are connected in series with a 4.0Ω resistor R, first as in circuit (i), and secondly as in circuit (ii).
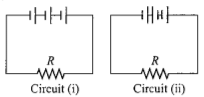
What is the ratio 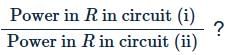
- a)9.0
- b)7.2
- c)1.8
- d)3.0
Correct answer is option 'A'. Can you explain this answer?
Three identical cells, each having an e.m.f. of 1.5 V and a constant internal resistance of 2.0Ω, are connected in series with a 4.0Ω resistor R, first as in circuit (i), and secondly as in circuit (ii).

What is the ratio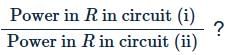

What is the ratio
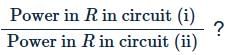
a)
9.0
b)
7.2
c)
1.8
d)
3.0

|
Mohit Rajpoot answered |
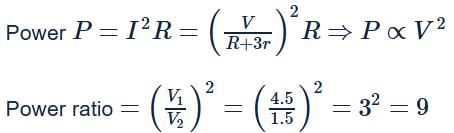
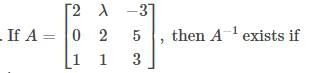
- a)λ = 2
- b) λ ≠ 2
- c) λ ≠ – 2
- d)None of these
Correct answer is option 'D'. Can you explain this answer?
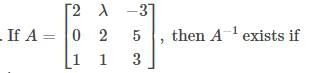
a)
λ = 2
b)
λ ≠ 2
c)
λ ≠ – 2
d)
None of these
|
|
Rajesh Gupta answered |

Correct option is D.
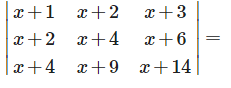
- a)–2
- b)0
- c)x+2
- d)none of these
Correct answer is option 'B'. Can you explain this answer?
a)
–2
b)
0
c)
x+2
d)
none of these

|
Ipsita Sen answered |
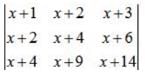
Apply , C1 → C1 - C2, C2 → C2 - C3,
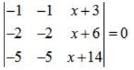
Because here row 1 and 2 are identical
If f(x) = 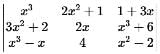 for all x ∈ R, then 2f(0) + f'(0) is equal to
for all x ∈ R, then 2f(0) + f'(0) is equal to- a)48
- b)24
- c)42
- d)18
Correct answer is option 'C'. Can you explain this answer?
If f(x) = 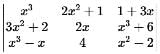 for all x ∈ R, then 2f(0) + f'(0) is equal to
for all x ∈ R, then 2f(0) + f'(0) is equal to
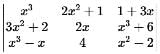 for all x ∈ R, then 2f(0) + f'(0) is equal to
for all x ∈ R, then 2f(0) + f'(0) is equal toa)
48
b)
24
c)
42
d)
18

|
Tarun Kaushik answered |
f(0) =  = 0
= 0
f'(x) =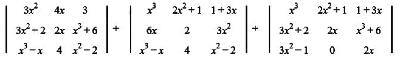
∴ f'(0) =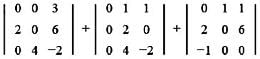
= 24 - 6 = 18
∴ 2f(0) + f'(0) = 42
 = 0
= 0f'(x) =
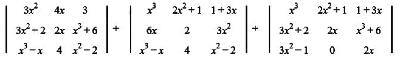
∴ f'(0) =
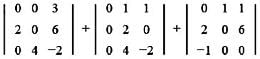
= 24 - 6 = 18
∴ 2f(0) + f'(0) = 42
If A is a symmetric matrix, then At =- a)A
- b)|A|
- c)0
- d)diagonal matrix
Correct answer is option 'A'. Can you explain this answer?
If A is a symmetric matrix, then At =
a)
A
b)
|A|
c)
0
d)
diagonal matrix

|
Nipun Tuteja answered |
If A is a symmetric matrix then by definition AT=A
Option A is correct.
Option A is correct.
Chapter doubts & questions for June Week 2 - Weekly Tests for JEE Preparation 2025 is part of JEE exam preparation. The chapters have been prepared according to the JEE exam syllabus. The Chapter doubts & questions, notes, tests & MCQs are made for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests here.
Chapter doubts & questions of June Week 2 - Weekly Tests for JEE Preparation in English & Hindi are available as part of JEE exam.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free.
Related JEE Content

Contact Support
Our team is online on weekdays between 10 AM - 7 PM
Typical reply within 3 hours
|
Free Exam Preparation
at your Fingertips!
Access Free Study Material - Test Series, Structured Courses, Free Videos & Study Notes and Prepare for Your Exam With Ease

 Join the 10M+ students on EduRev
Join the 10M+ students on EduRev
|

|
Create your account for free
OR
Forgot Password
OR
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup





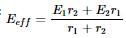
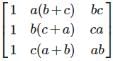 , then Det. A is
, then Det. A is